基于UPF的WNN學習算法及其應用

魏燕明，甘旭升，張 鐵，楊國洲，席 新

（1.西京學院，西安710123；2.空軍工程大學空管領航學院，西安710051；3.北方聯創通信有限公司，南昌330000）

0 引言

小波網絡（Wavelet Neural Network，WNN）是一種有別于傳統神經網絡的學習方法，其由小波變換推導而來，學習能力強，收斂速度快，也適用于傳統神經網絡應用的所有領域。

發揮WNN潛在性能，選擇合適學習算法至關重要，這也是當前該領域研究的熱點。除了傳統的BP學習算法外［1］，粒子濾波（Particle Filter，PF）算法也可用于WNN學習。PF是一種基于Bayes理論的非線性遞歸估計方法，適用于狀態空間模型描述的非高斯背景的任意非線性系統［2］。但其性能的好壞依賴于所選擇的重要性密度函數（Importance Density Function，IDF），研究表明，采用無跡Kalman濾波（Unscented Kalman Filter，UKF）生成IDF，濾波效果更好，但其運算量偏大［3］。而降低UKF運算量的最佳途徑，是在確保估計精度前提下，在無跡變換（Unscented transforma-tion，UT）中，選取適當采樣策略減少點個數［4］。

基于以上分析，在采用UKF算法產生PF算法的重要性函數過程中，引入一種改進的Sigma點采樣策略，以期減少運算量，有效地提高WNN的學習效率。并通過某型軍用飛機的氣動力建模算例進行了驗證。

1 無跡卡爾曼濾波（UKF）

UKF就是UT在Kalman濾波中的應用。UT是UKF的核心。UT是一種計算非線性變換中的隨機變量的統計特征的新方法。它用固定數量的參數去近似一個高斯分布，而省去了繁瑣的雅可比與海森矩陣的計算過程。數值分析表明，UT中選取Sigma點個數的多少，對UKF的估計精度和計算量有很大影響。選取的Sigma點個數越多，UKF估計就越準確，相應的計算量也會越大。文獻［5］研究指出，在UT選取Sigma點個數過程中引入最小偏度（Minimal Skew）概念，即SUT，能夠以犧牲較小精度前提下，顯著改善計算效率。其點采樣步驟如下：

2）選取Sigma點權值

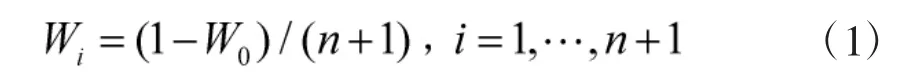
3）初始化序列

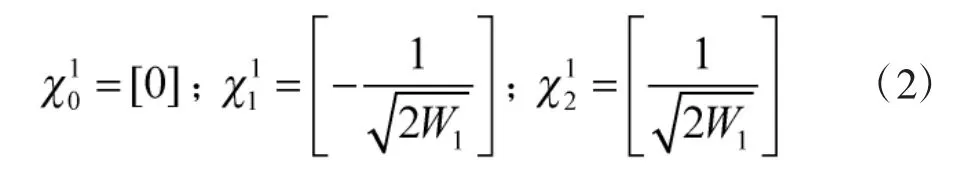
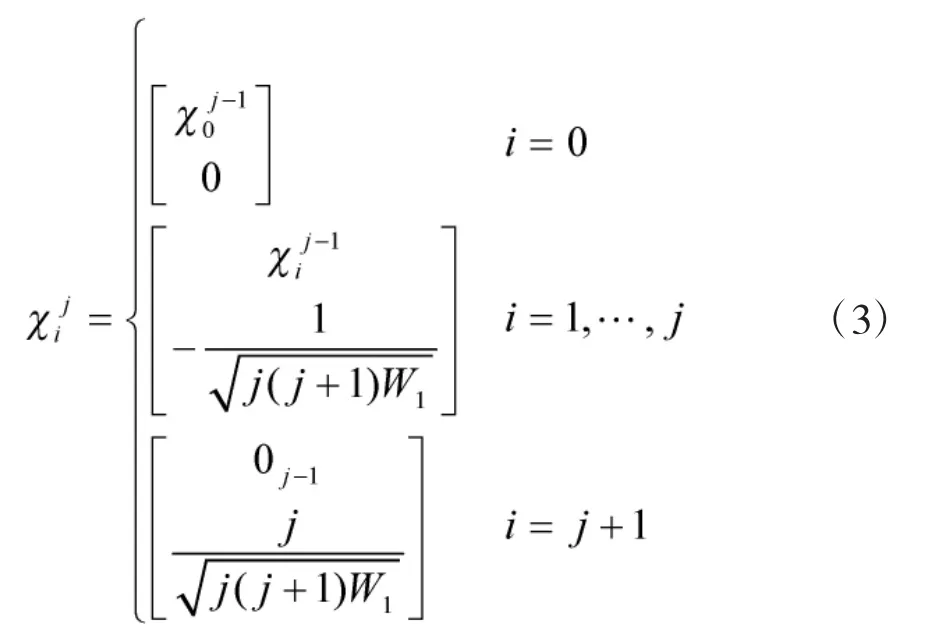
5）將均值和方差信息與Sigma點集成

根據以上過程可知，基于SUT的UKF，即SUKF。其整個計算過程無需了解非線性函數細節，其對均值和協方差的估計精度與基于UT的UKF大體相當，且計算量明顯減少。

2 SUPF算法

PF是在Monte Carlo法基礎上發展起來的一種Bayes濾波［6］。它使用狀態空間中若干加權隨機粒子來逼近系統狀態的后驗概率密度函數（Posterior Density Function，PDF），對非高斯系統狀態與參數估計具有較大優勢。PF算法的關鍵是IDF的選取。

PF的IDF越逼近PDF，精度越逼近最優，估計值也越穩定，但如何獲取合適的IDF是一個亟待解決的難題。標準PF主要采用狀態轉移概率密度函數進行重要性采樣，粒子嚴重依賴狀態轉移模型的選取。若模型選取不準，可能導致非常大的采樣偏差。為此，需要探索更接近于PDF的IDF。文獻［7］提出通過EKF算法計算IDF的PF算法，即EPF算法，其可逼近于一階Taylor級數；文獻［8］在PF中采用UKF算法選取IDF，即UPF算法，濾波精度更高，狀態均值和方差可近似到三階，但其需要UT，計算量偏大。由前述可知，SUKF算法是UKF算法的改進，兩者精度大體相當，但前者運算量卻顯著降低，因此，采用SUKF算法產生重要性密度函數（SUPF算法），理論上可取得與UKF算法相近的PF性能，并明顯改善計算效率。基于此，可有SUPF算法流程：

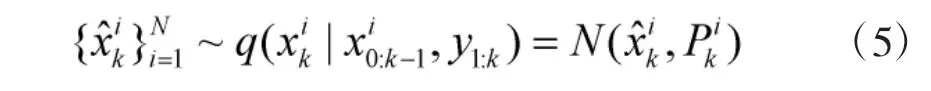
②計算粒子權值

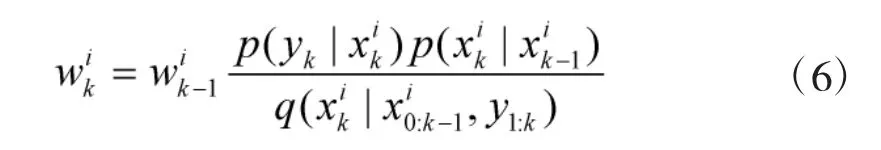
③粒子權值歸一化

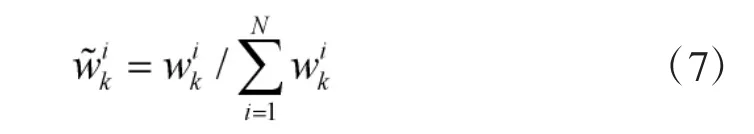
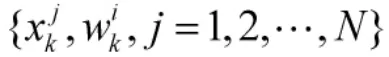
4）輸出結果

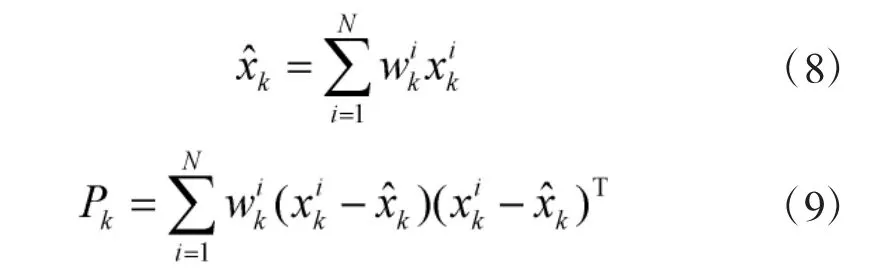
5）k=k+1，并轉到步驟2）。

3 基于SUPF的WNN學習算法

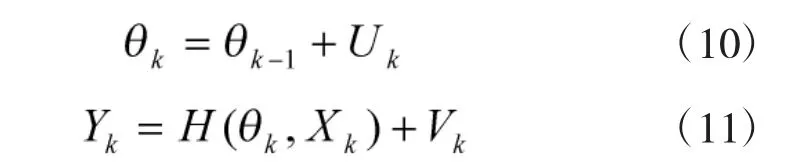
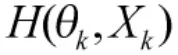
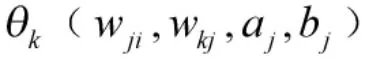
4 仿真分析

4.1 非線性系統辨識

設給定的SISO非線性系統為：

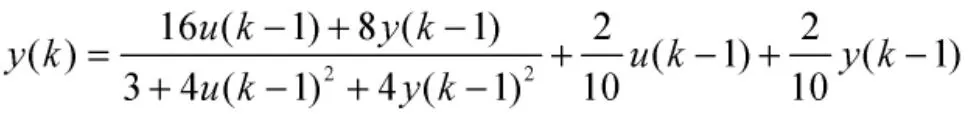
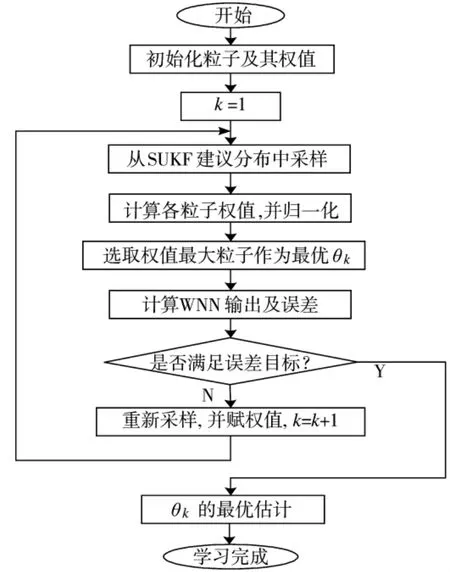
圖1 SUPF-WNN實現流程

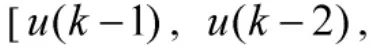
使用7種算法進行WNN學習的20次平均訓練時間和測試平方根誤差（MSE）對比如下頁表1所示。當粒子數目N分別取50，100，150,200，250時，4種PF算法的WNN測試MSE和訓練時間對比如圖2和圖3所示。圖4給出SUPF算法的WNN訓練收斂曲線。

從仿真結果可看出：相對于傳統BP算法，其余6種算法都提升了WNN性能，說明使用濾波估計技術確實能夠有效降低系統引起的偏差。由于線性化過程中引入了模型誤差，基于EKF算法的WNN性能并不如UKF算法，這與UT改進EKF的理論分析結論相一致。而使用UPF算法進行WNN學習，較之SPF與EPU算法效果更好，其主要原因有兩個：其一，UPF算法能夠充分利用最新觀測到的信息；其二，它利用UKF算法選取IDF，更逼近于PDF，可精確到Taylor級數的三階。需要指出的是，UPF算法的計算量與UT變換的Sigma點個數成正比，這使得UPF-WNN需要更多的學習時間。而SUPF-WNN的測試精度與UPF-WNN相當，但后者是在較少Sigma點情況下獲得的，學習時間明顯減少。主要原因是，SUPF在利用傳統UKF產生IDF時，由SUT替代了對稱分布Sigma點的UT，在繼承UKF良好性能的同時，很大程度降低了計算量。

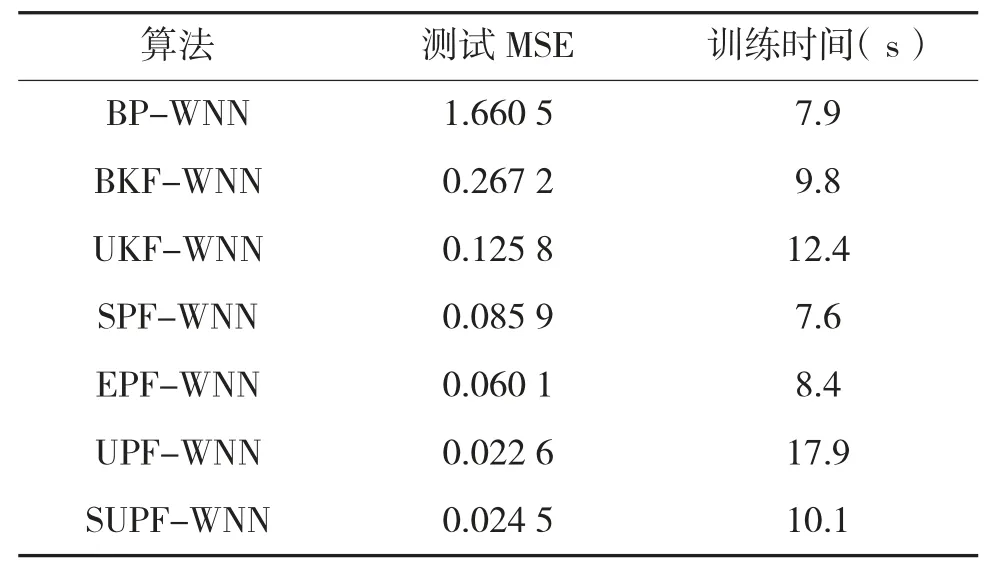
表1 基于各學習算法的WNN性能對比

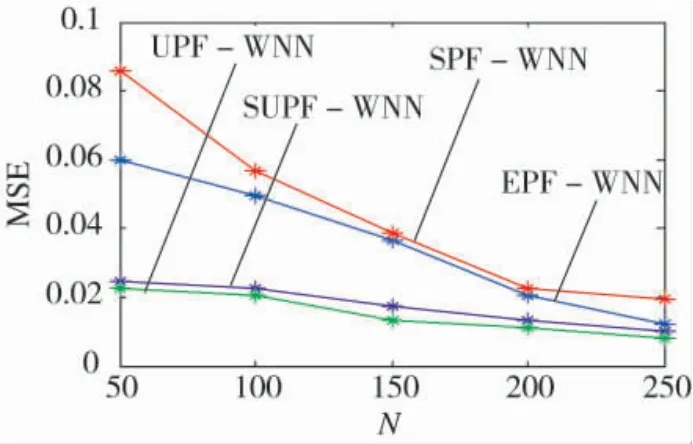
圖2 粒子數目對WNN測試性能的影響

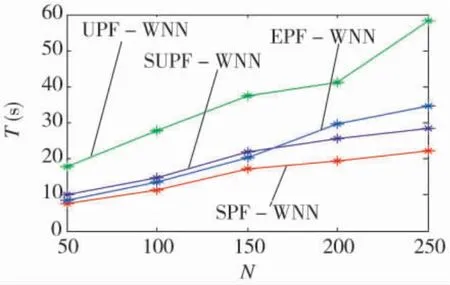
圖3 粒子數目對WNN訓練時間的影響

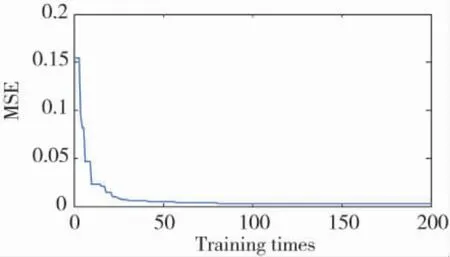
圖4 基于SUPF-WNN算法的WNN訓練收斂曲線

4.2 飛行器氣動力建模

為深入驗證SUPF-WNN的性能及其實用性，將其引入某型軍用飛機的氣動力建模實驗，分為橫側向建模和縱向建模兩方面的測試。飛行實測數據來源于空中飛行模擬機ATTAS的副翼、方向舵和升降舵輸入激勵產生的兩個機動動作［10］。在實驗中，隱層節點取為15，其他參數設置同4.1，為消除量綱的影響，建模前先對飛行數據作標準化處理，部分變量解釋如圖5所示。

ATTAS的橫側向氣動力模型可表示為

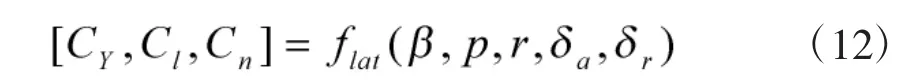
式中，β為側滑角，p為傾斜角速率，r為偏航角速率，δa為副翼偏轉角，δr為方向舵偏轉角，部分變量解釋如圖5。而CY、Cn和Cl分別為側力系數、偏航力矩系數和滾轉力矩系數，可根據文獻［14］提供的方法計算得出。

ATTAS的縱向氣動力模型可表示為

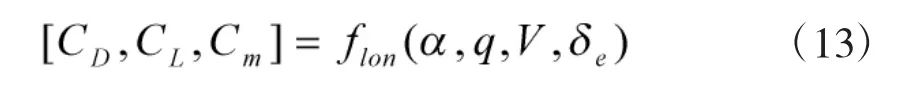
式中，α為攻角，q為俯仰角速率，V為真速，δe為升降舵偏轉角。而CD、CL和Cm分別為阻力系數、升力系數和俯仰力矩系數，可根據文獻［11］提供的方法計算得出。

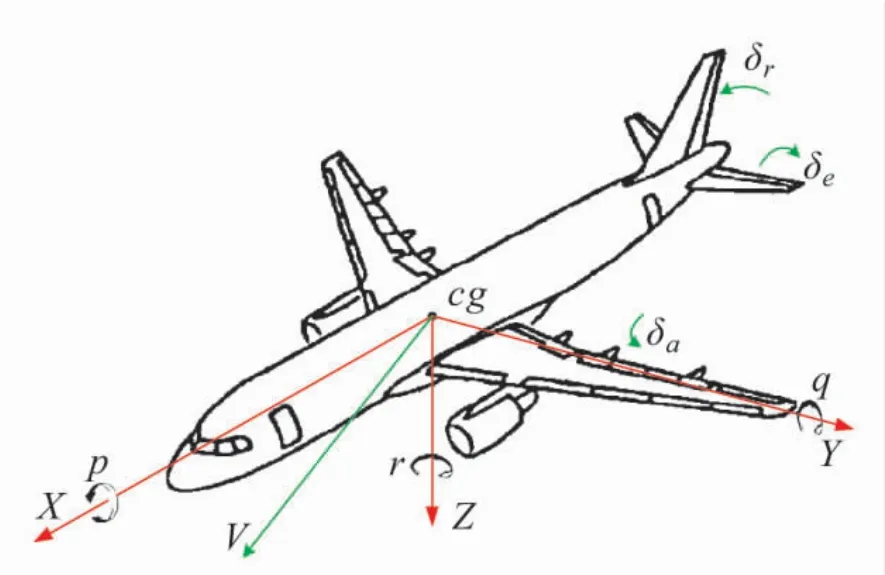
圖5 部分變量的符號解釋

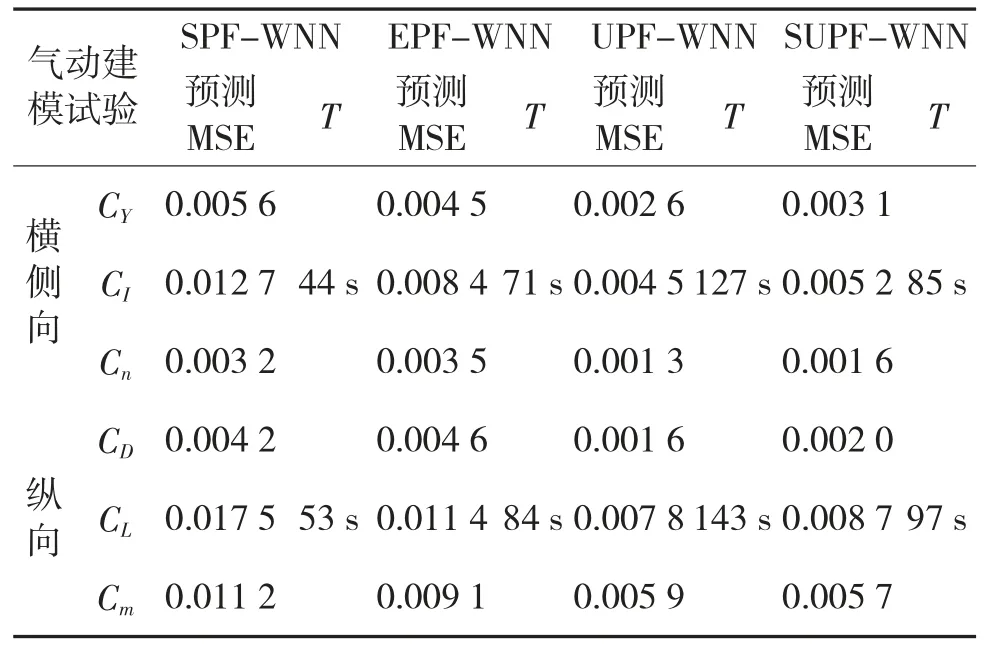
表2 氣動力建模的仿真結果對比

從表2和圖6的實驗結果可得出與4.1大致相同的結論，基于SUPF學習算法的WNN，在測試MSE方面明顯優于SPF-WNN和EPF-WNN，與UPF-WNN大體相當，但訓練時間（T，單位：s）方面要優于UPF-WNN。這再次驗證了采用新Sigma點采樣策略的UKF來選取IDF，不僅能夠保持UPF算法在WNN學習中的優良性能，而且減少了計算量，縮短了學習時間，從而為解決飛行器的氣動力WNN建模問題提供了方法與技術上的支持。

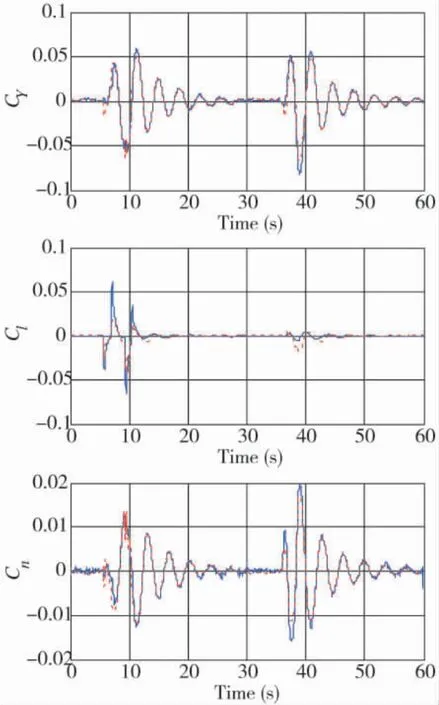
圖6 橫側向氣動模型預測結果

5 結論

為改善WNN訓練效率，對其狀態空間模型引入一種改進UKF的PF學習算法。首先，將基于最小偏度Sigma點采樣策略的UT用于改進UKF算法，以代替傳統計算量較大的對稱分布Sigma點采樣的UT，然后，采用改進UKF算法選取PF算法的重要性密度函數，進而對WNN參數進行最優估計，完成WNN訓練。仿真結果表明，該PF學習算法可較好地提高WNN的性能，縮短模型訓練時間，提高建模效率。同時，也為復雜系統的建模預測提供了一種可靠的解決方法。