改進近似動態規劃法的攻擊占位決策*

姜龍亭，寇雅楠，王 棟，張彬超，胡 濤

（1.空軍工程大學航空工程學院，西安710038；2.解放軍95974部隊，河北 滄州061000；3.解放軍95356部隊，湖南 耒陽421800）

0 引言

近年來，無人機技術發展迅猛，已經在經濟和軍事領域有了一定的應用。目前，大多數的空戰任務主要是由有人機來完成。但是由于近距空戰激烈的對抗性和動態特性，人在回路的無人機以及有人機在面臨復雜的戰場情況時，常常因為誤判態勢造成空戰失利。同時，由于自主決策系統能將飛行員從緊張、激烈的對抗任務中解脫出來，對武器裝備的發展以及人類的發展進步都具有深遠的意義。因此，研究具有自主機動決策的無人機成為各軍事強國爭先發展的重點。

自主空戰決策［1］是指對抗過程中，為了實現優勢態勢和最小化我機面臨的危險，實時地計算出無人機的最優機動策略。目前，學者們針對無人機自主決策問題提出了許多方法。主要有微分對策法、影響圖法、專家系統法和強化學習法。基于微分對策法［2-4］的決策系統由于受限于具體的數學模型，可移植性較差；影響圖法［5］在一定程度上對空戰給出了合理的決策行為，但是沒有通過全局的戰場態勢信息構建決策模型，無法滿足高強度的空戰需要，很難應用到實戰中；專家系統法［6-7］通過建立態勢與機動策略的映射關系來模擬飛行員的決策過程，但是專家系統難以構建完備的規則模型，并且通用性較差；神經網絡法［8-9］求解得到的機動決策無法從模型本身進行合理解釋，并且需要大量的實戰訓練樣本數據。

本文主要針對空戰過程的攻擊占位決策問題進行研究。由于近似動態規劃法［10-14］具有良好的泛化能力和在線學習能力，本文在前期研究的基礎上，通過對戰場環境和戰術使用原則的分析，建立基于近似動態規劃的空戰機動決策模型。文獻［10］通過對近似動態規劃法的研究，解決了航模的追逃問題，但是真實的空戰過程有著不同與航模的高機動性的特點。文獻［13］雖然通過近似動態規劃法對水平飛行的空戰接敵問題進行了研究，但是在占位決策過程中，由于未考慮飛機的過沖問題，智能體在機動決策后容易進入敵方攻擊區內。針對上述存在的不足，本文通過對空戰過程分析，提出懲罰因子對近似動態法進行改進，建立改進的近似動態規劃模型，避免了攻擊占位過程中的“過沖”現象。

1 問題描述

正如著名軍事理論家杜黑所言：空戰就是以奪取制空權為最終目的對抗過程。作戰雙方的作戰目的就是在避免被對方擊落的情況下，占據攻擊對方的戰術優勢位置。這種戰術優勢位置隨著敵我雙方的相對位置在空間里連續變化。為了清晰描述態勢的動態變化過程，某一時刻紅藍雙方的幾何占位態勢信息如圖1所示。

圖1 紅藍雙方幾何占位態勢圖

算法1：狀態轉移函數計算方法

初始化：

For i=1：5（仿真步長為Δt=0.375 s）

算法1中，st為當前時刻輸入的狀態信息，根據狀態轉移方程求解，st+1即為下一時刻的狀態信息。

求解自主攻擊的占位決策問題實質上是一個序列決策問題。即基于當前的態勢信息給出一種最優的機動決策序列，也即求解空間狀態與機動行為之間的一種映射，使得飛機快速朝著攻擊的優勢位置飛行，最終完成攻擊敵機的任務。

2 近似動態規劃法

2.1 近似動態規劃法基本框架

由于動態規劃法具有良好的泛化和在線學習能力，在解決序列決策問題上有著很大的優勢。利用動態規劃法求解序列決策問題時，需要建立長期收益與狀態之間的映射關系。對于離散的低維度狀態空間，各個狀態的長期收益可以保存在查詢表內。但是，隨著戰場環境和空戰任務的日益復雜，基于查詢表式的長期收益顯得捉襟見肘。尤其是在解決具有連續性狀態空間的空戰決策問題更是容易出現“維數災難”。為了解決狀態維數高造成的問題，近似動態規劃法基于函數擬合的思想，以連續函數逼近長期收益的狀態值函數。通過嚴密的數學推導，對長期收益值函數進行逼近優化，由此獲得狀態空間與長期收益值之間的映射關系。

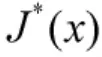
則近似值函數可作為線性回歸的觀測值，即

為了清楚地對空戰狀態進行描述，采樣狀態的特征集合記為：

其中，M為狀態特征的數目。

基于函數擬合的思想，采樣狀態和近似值函數可以抽象為一個多元線性回歸問題，即

使用標準最小二乘估計進行計算，

由此可得，第i次迭代后的長期收益值函數為：

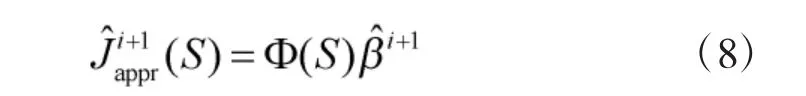
2.2 獎勵函數

空戰過程中，紅藍雙方在各自的戰術策略下首先隱蔽接敵，然后攻擊占位。通過控制飛機快速進入敵方的尾后區域，并截獲跟蹤目標，直至發射導彈。為了準確控制飛機快速占據攻擊敵方的優勢位置，本文從空戰的隱蔽接敵和攻擊占位兩個階段對上述提出的獎勵函數進行定義。因此，獎勵函數R（s）包括即時獎勵函數G（s）和態勢獎勵函數A（s）兩部分。

一是即時獎勵函數。即將敵方的尾后區域定義為占位的目標區域，通過獎勵進入占位目標區域的狀態引導飛機進入攻擊位置。目標區域（見圖2）往往與飛機的性能密切相關。在本文中，主要考慮飛機的提前角ATA、進入角AA和雙方的相對距離r。因此，依據文獻［10］的分析，即時獎勵函數G（s）定義為：

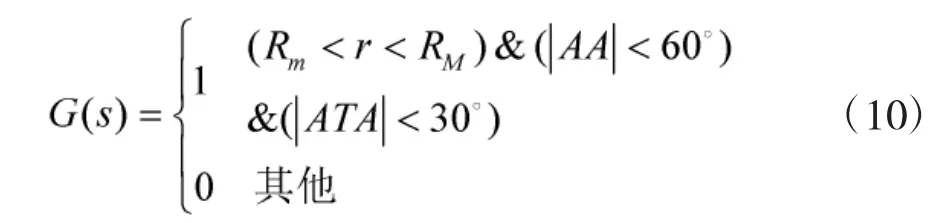
圖2 藍方攻擊優勢區域示意圖

圖2所示虛線區域表示當藍方飛機的進入角小于60°，提前角小于30°，兩機距離在武器系統的作用范圍內時，無論藍方采取何種機動，藍方都占據優勢地位，并且可以以較高的命中率發射導彈。近似動態規劃法通過即時獎勵函數G（s）對優勢攻擊位置獎勵，將引導藍方飛機快速進入定義的優勢攻擊位置。

二是態勢獎勵函數。即當飛機在隱蔽接敵過程中對空戰態勢優勢的獎勵。飛機在空戰過程中可以通過態勢獎勵函數引導飛機向空戰區域機動。態勢獎勵函數A（s）的定義將彌補即時獎勵函數不連續性的缺點。由于本文只考慮平面等高度下的空戰對抗，且雙方速度假設恒定，因此，態勢獎勵函數主要與敵我雙方的相對角度和距離相關。態勢獎勵函數A（s）定義為：

結合即時獎勵函數和態勢獎勵函數，近似動態規劃法中的獎勵函數R（s）定義為：

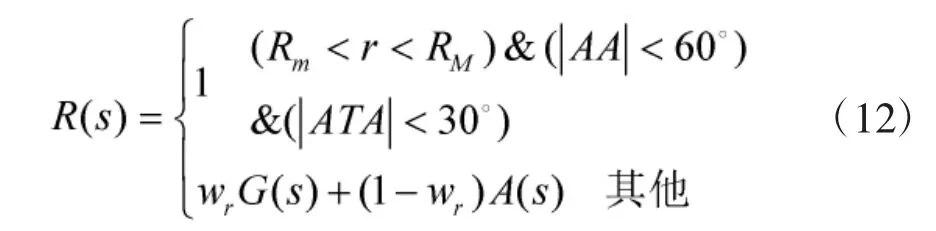
其中，wr為即時獎勵函數與態勢獎勵函數之間的權重因子。即時獎勵函數引導飛機進入攻擊占位優勢區域；態勢獎勵函數在整個狀態空間發揮作用，在空戰過程中，引導飛機朝著優勢區域飛行。

2.3 懲罰因子

理想的空戰決策問題需要在獲得獎勵的同時也要平衡在機動過程中存在的風險。由于近似動態規劃法在機動決策時，僅考慮了如何將飛機引導至己方優勢區域，依據幾何關系定義了優勢函數，未對飛機的危險區域進行定義，并且因為策略搜索算法有限的前瞻性，較短的搜索范圍也容易陷入局部最優，仿真分析和飛行機動決策過程中容易造成“過沖”，使得飛機處于敵方的優勢區域內。當藍方處于紅方的優勢區域時間越長，相對距離越近，藍方被紅方擊中的幾率也就越大。為了克服上述存在的不足，本文針對“過沖”問題和距離太近引起的“碰撞”問題，結合空戰實際問題，定義了與獎勵函數對應的懲罰函數P（s）。

空戰過程中，進入敵方攻擊區的概率也是隨機的，為了描述這種隨機性，定義了風險概率pt（s）：

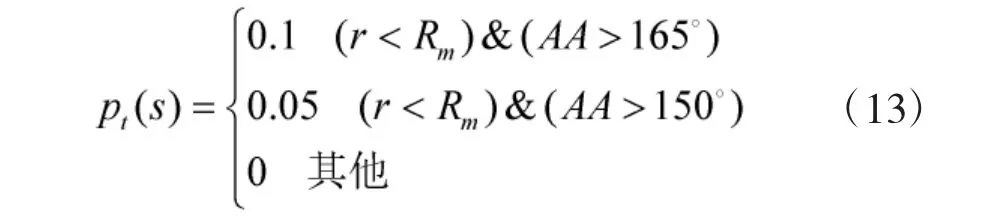
為了避免距離太近引起的兩機相撞問題，對pt進一步改進，改進后的風險概率P（s）為：

例如，當飛機的相對距離小于武器的最小發射距離，AA=180°時，危險概率P=0.1。也就是說在現實世界中飛機進入敵方飛機的攻擊區域，被敵方攻擊的概率是0.1。隨著雙機距離逐漸接近，危險概率P（s）越來越大。危險概率P（s）將阻止藍方飛機進入紅方的攻擊區域。

為了防止飛機在飛行過程中因“過沖”進入敵方的攻擊區域，本文基于懲罰函數對長期收益值函數式（9）進行了修正：

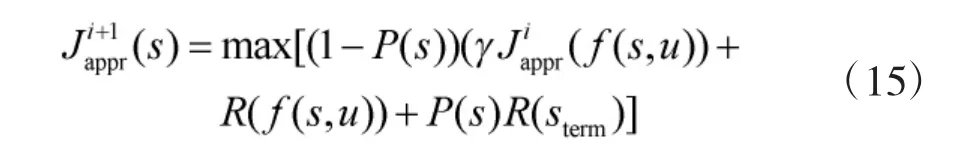
如果當前狀態P（s）＞0時，則表示藍方飛機處于敵方的攻擊區域內。通過減小長期收益值，引導藍方飛機進行快速擺脫。也即藍方飛機一旦進入敵方的優勢區域內，將快速機動至敵方的攻擊優勢區域外。

改進后的近似值函數計算如算法2：

算法2：改進的近似值函數計算

2.4 狀態采樣

近似動態規劃法逼近長期收益值，需要對空戰博弈的狀態空間進行采樣。采樣稀疏對近似值函數Jappr（s）與值函數J*（s）的誤差有著至關重要的影響。只有最大限度地減小最優值函數與值函數的誤差，求解的機動策略才最接近最優的機動策略。從這個角度出發，高密度的采樣將比低密度的采樣更接近最優解，但是采樣數的增多必然帶來計算量指數增加。并且，采樣數目的增多，執行貝爾曼迭代所需要的時間也大幅增加，必然會對機動決策的實時性產生很大的影響。從這個角度出發，采樣的狀態數目應該是越少越好，低密度的采樣將會使得智能體的運算速度較快，決策的實時性將得到提升。因此，為了平衡機動策略的誤差與決策實時性這一對矛盾，必須合理地選擇采樣點。在重要的狀態空間區域，有必要進行精細的狀態采樣；在很小幾率出現的狀態空間區域，則沒必要劃分太精細。為了確保空戰過程中最有可能出現的區域得到充分的采樣，本文對飛機空戰過程進行軌跡采樣［10］。

2.5 機動策略提取

在紅藍雙方仿真對抗過程中，紅方采取最大最小策略進行機動決策，藍方采取近似動態規劃方法進行機動決策。則藍方的機動策略為：

算法3：機動策略提取

輸入：si

基于改進的近似動態規劃法可以依據最優的長期收益值進行決策，而不是通過有限的前瞻策略進行決策，并且以懲罰函數對收益值函數進行修正。因此，基于ADP的機動決策不僅能反映空戰全局的最優決策，而且還能有效避免“過沖”問題和“碰撞”問題。

3 仿真分析

仿真1假設紅方飛機未能有效感知戰場態勢，依然保持初始航向和初始機動策略飛行。藍方飛機根據所處戰場態勢，使用基于ADP的機動策略。紅藍雙方初始狀態信息見表1。

表1 紅藍雙方初始態勢信息表

仿真如下頁圖3所示。

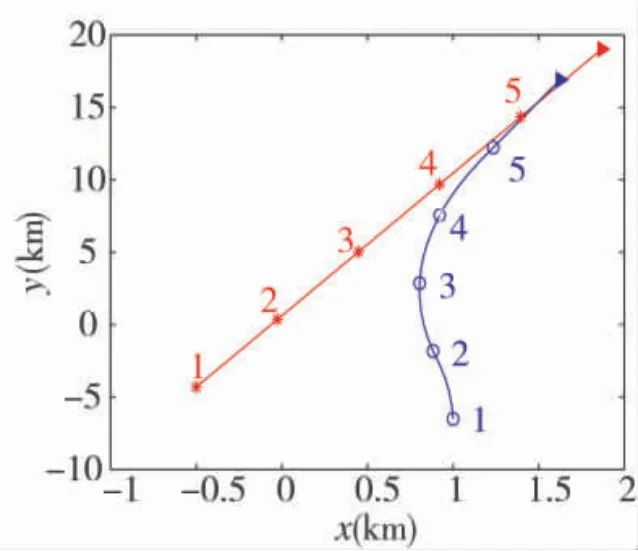
圖3 仿真驗證1結果

從圖3可以看出，在紅方保持機動方向不變的情況下，藍方通過ADP機動策略能夠很快機動至紅方的尾后攻擊區域，有效占據攻擊優勢。

仿真2假設紅方飛機能有效感知戰場態勢，并且根據戰場態勢以最大最小的機動策略與藍方飛機進行對抗。藍方飛機根據所處的戰場態勢，使用基于ADP的策略進行機動決策。紅藍雙方初始初始狀態信息見表1。

仿真如圖4所示。

圖4 仿真驗證2結果

從圖4可以看出，在紅方采取最大最小策略進行機動，藍方通過ADP機動策略能夠很快機動至紅方的尾后攻擊區域，有效占據攻擊優勢。

仿真3假設紅方飛機能有效感知戰場態勢，并且根據戰場態勢以最大最小的策略進行機動決策，藍方飛機根據所處的戰場態勢，在使用基于ADP的策略與紅方飛機對抗時存在“過沖”機動，于是使用改進的ADP策略確保不處于紅方的優勢區域，并且快速占據優勢攻擊位置。紅藍雙方初始狀態信息如表2所示。

表2 紅藍雙方初始態勢信息

仿真如圖5所示。

從圖5中可以看出，當紅方采取最大最小策略，藍方采取ADP策略時，藍方由于提前采取左轉機動，在第4次機動決策后，造成“過沖”現象，此時紅方呈尾追態勢，若鎖定目標，即可對藍方實施攻擊。在同樣的初始條件下，藍方依舊采取最大最小策略，紅方采用改進之后的ADP策略時，最優機動決策則是先維持初始航向，然后再采取左轉盤旋機動。通過仿真可以發現，藍方在第5次機動決策后，占據尾追攻擊的優勢態勢，有效避免了“過沖”問題。

圖5 仿真驗證3結果

4 結論

本文基于近似動態規劃法理論對水平飛行、定速、一對一空戰自主攻擊占位決策方法進行了研究。基于近似動態規劃理論建立了空戰自主攻擊占位的決策框架。針對空戰環境的高維度狀態空間，基于函數擬合的思路構建近似值函數，對空戰過程的長期收益逼近優化，給出了自主攻擊占位決策的策略學習方法；對傳統的近似動態規劃決策方法存在的“過沖”和“碰撞”問題，提出了懲罰因子對近似動態規劃法進行改進。仿真結果表明，改進的近似動態規劃法在自主攻擊占位決策中，可以有效避免發生“過沖”和“碰撞”問題。

基于改進的近似動態規劃法在自主攻擊占位決策時，近似值函數的優劣對策略學習有著至關重要的影響。確定合理的長期收益值函數將能逼近最優的值函數，進而得到最優的機動策略。同時，在進行策略學習時，藍方機動策略的優越性依賴于紅方飛機的智能化水平。紅方的智能化水平越高，藍方學習到的機動策略將更具魯棒性和智能性。因此，在后續的研究中，提高藍方飛機機動策略的智能性以及逼近最優的值函數，將進一步提升飛機的自主空戰能力。