水下航行器軸向運(yùn)動的初始修正自適應(yīng)反演控制方法*

余有芳，嚴(yán)求真，蔡建平

（1.浙江商業(yè)職業(yè)技術(shù)學(xué)院應(yīng)用工程學(xué)院，杭州310053；2.浙江水利水電學(xué)院信息工程學(xué)院，杭州310018；3.浙江水利水電學(xué)院電氣工程學(xué)院，杭州310018）

0 引言

作為一種水下機(jī)器人，自主水下航行器如今已應(yīng)用于科學(xué)研究、企業(yè)民用和軍事等領(lǐng)域，執(zhí)行著諸如深海勘探開發(fā)、水文數(shù)據(jù)采集、水下搜救、海戰(zhàn)偵察攻擊等任務(wù)［1-2］。隨著自主水下航行器應(yīng)用范圍的不斷擴(kuò)大，水下航行器軸向控制問題，引起了人們的關(guān)注［3］。研究航行器軸向運(yùn)動精確控制方法，實現(xiàn)對參考信號的精確跟蹤，有助于自主水下航行器高質(zhì)量地完成偵察、水下測量和目標(biāo)跟蹤等任務(wù)，因而是一項有意義的工作。

自主水下航行器往往在復(fù)雜的水下環(huán)境中航行，要對其進(jìn)行精確建模是一件困難的工作。針對自主水下航行器的控制方法研究可追溯到20世紀(jì)90年代初，早期的結(jié)果多為PID控制方法［4］。本世紀(jì)以來，人們著手探討水下航行器的先進(jìn)控制方法。Smallwood等研究忽略海流影響情形下的自主水下航行器自適應(yīng)控制方法［5］。在文獻(xiàn)［6］中，Riedel為水下航行器設(shè)計滑模變結(jié)構(gòu)控制器，但沒有進(jìn)行穩(wěn)定性分析。Gao等研究水下航行器在受海流影響情形下的軸向運(yùn)動軌跡跟蹤問題，給出了自適應(yīng)反演滑模控制器設(shè)計和自適應(yīng)積分反演控制器設(shè)計兩種方案［7-8］。

水下航行器在執(zhí)行跟蹤任務(wù)時，航行器的起始位置常常不在參考軌跡的起點。當(dāng)航行器的質(zhì)量和初始誤差均較大時，在執(zhí)行跟蹤任務(wù)的起始時間段內(nèi)，采用常規(guī)控制方法實現(xiàn)跟蹤任務(wù)需要航行器系統(tǒng)能夠提供較大的輸出動力。這一期望輸出動力有時甚至超過航行器動力系統(tǒng)的最大輸出，導(dǎo)致理論算法在具體實施時無法獲得較好的收斂結(jié)果。因此，改善或緩解這一矛盾，是一件有意義的工作，是開展本文所述研究工作的動機(jī)。

本文研究水下航行器的自適應(yīng)反演控制方法，主要工作與創(chuàng)新之處在于：1）利用傳統(tǒng)自適應(yīng)反演控制方法為自主水下航行器設(shè)計控制器，并進(jìn)行分析；2）為了克服傳統(tǒng)自適應(yīng)控制算法在實施時，由于航行器質(zhì)量和初始誤差較大所導(dǎo)致的期望輸出推力過大現(xiàn)象，本文在給出修正信號構(gòu)造方法的基礎(chǔ)上，提出初始修正自適應(yīng)反演控制方法，對此予以改善。

1 問題的提出

考慮解耦后的水下航行器的軸向運(yùn)動模型

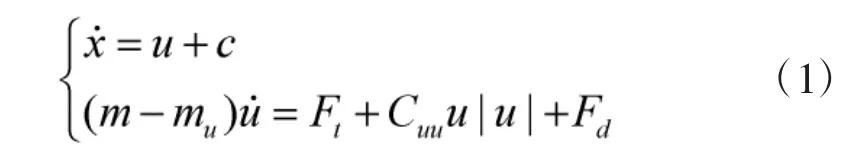
式中，x和u分別表示水下航行器的軸向位移和相對海流的前進(jìn)速度，c為未知的常值海流速度，m和mu分別為航行器本身的質(zhì)量和流體附加質(zhì)量，Cuu為流體二次阻尼系數(shù)，F(xiàn)t為航行器系統(tǒng)的推力，F(xiàn)d代表外部常值擾動，m、mu和Cuu均為未知的正常數(shù)，m－mu＞0。

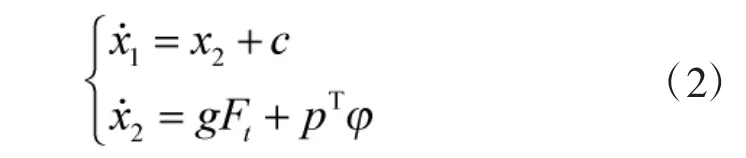
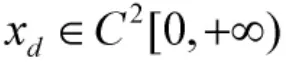
2 無初始修正的自適應(yīng)反演控制

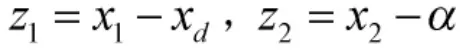
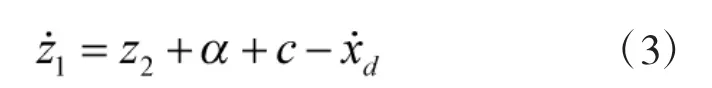
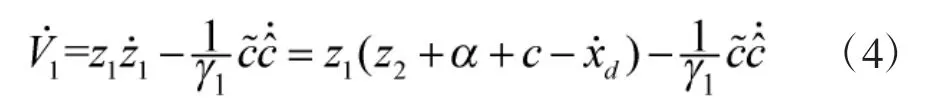
由于

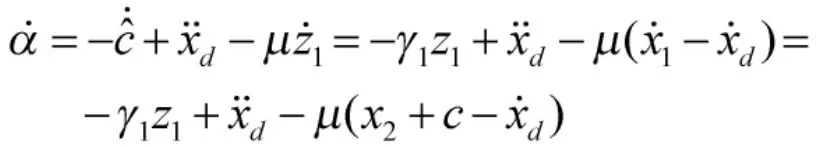
故

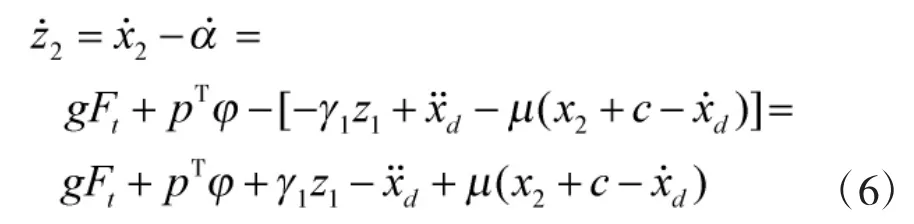
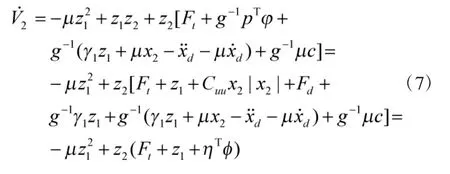
基于式（7），為系統(tǒng)式（2）設(shè)計控制律

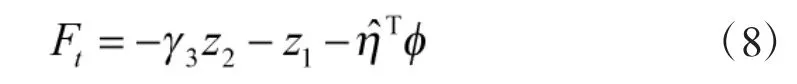
及自適應(yīng)律

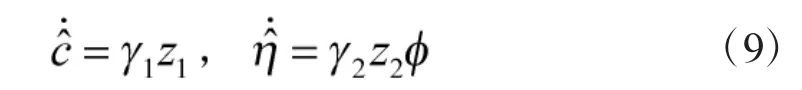
閉環(huán)系統(tǒng)具有的性質(zhì)可以總結(jié)為如下定理：

定理1將控制律式（8）及自適應(yīng)律式（9）施加于水下航行器軸向運(yùn)動系統(tǒng)式（2），可實現(xiàn)位置跟蹤誤差漸近收斂于零，并確保閉環(huán)系統(tǒng)所有信號有界。

證明選擇Lyapunov函數(shù)

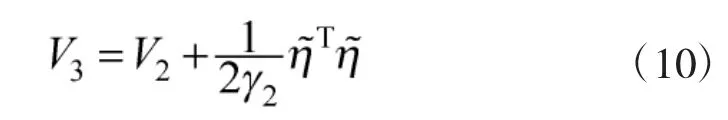
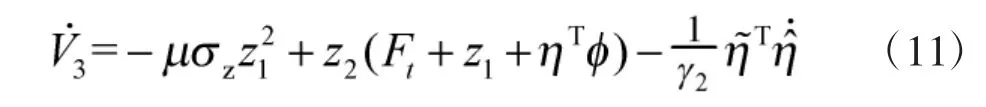
將式（8）和式（9）代入式（11），可得

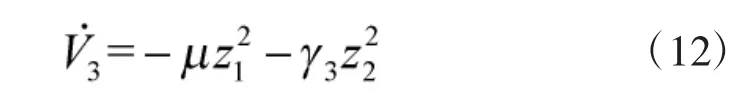
由式（12）可見，

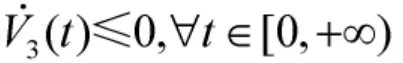
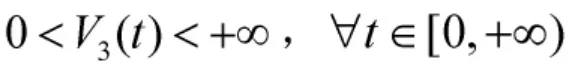
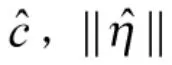
對式（12）的兩邊積分，有

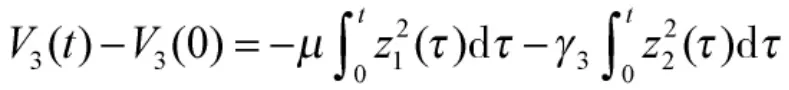
根據(jù)Lyapunov函數(shù)的非負(fù)性，由上式可以推出

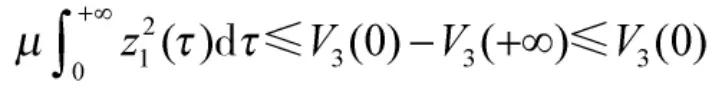
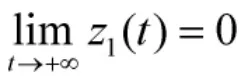
上文給出的控制設(shè)計方案中，利用自適應(yīng)方法估計未知常數(shù)，可以實現(xiàn)跟蹤誤差漸近收斂至零。在輸入增益較小（即航行器本身質(zhì)量較大）場合，且初始誤差較大場合，利用上文給出的控制方法設(shè)計控制器，往往需要較大的控制輸入，有時可能超過實際系統(tǒng)的最大輸出動力（本文將在數(shù)值仿真部分展示這一點）。針對這一問題，下一節(jié)對本節(jié)提出的算法進(jìn)行改進(jìn)。

3 初始修正自適應(yīng)反演控制

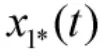
3.1 修正參考信號的構(gòu)造

借鑒文獻(xiàn)［9-11］，利用待定系數(shù)法，構(gòu)造曲線

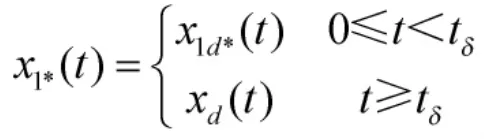
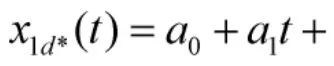
可以看出，這些曲線具有如下性質(zhì)：

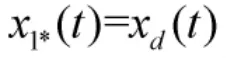
3.2 控制器設(shè)計

類似于上一節(jié)的式（8）和式（9），分別設(shè)計控制律及自適應(yīng)律為

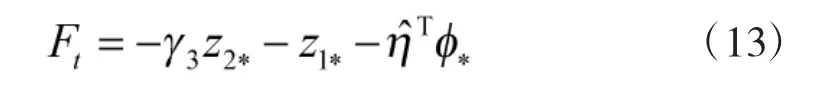
及

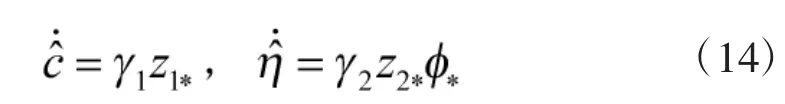
將控制器式（13）作用于系統(tǒng)式（2），具有如下性質(zhì)：

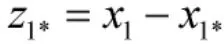
證明 與定理1的證明相類似，對Lyapunov函數(shù)

求關(guān)于時間的導(dǎo)數(shù)，即可得證。此處限于篇幅，略去詳細(xì)步驟。

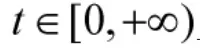
在本節(jié)給出的設(shè)計方法中，將原有的系統(tǒng)輸出對參考信號的跟蹤轉(zhuǎn)化為系統(tǒng)輸出對修正參考信號的跟蹤。這樣，原設(shè)計方案中可能出現(xiàn)的期望控制輸入量過大現(xiàn)象得到了改善。

4 仿真算例

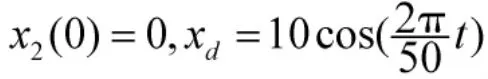
2）為了改善控制量過大的情況，采用飽和方法，將推力限幅在-10 KN到10 KN之間，其余仿真參數(shù)取值同前。仿真時長80 s，相應(yīng)結(jié)果見圖3和圖4。從圖3可見，航行器無法對參考軌跡進(jìn)行漸近跟蹤，從頭至尾，一直存在較大的跟蹤誤差，且誤差沒有收斂；由圖4可見，控制量即推力的顫振情況非常嚴(yán)重。

3）采用控制器式（13）進(jìn)行仿真，tδ=5，其余仿真參數(shù)取值同1），仿真時長30 s，相應(yīng)仿真結(jié)果見圖5和下頁圖6。可以看出，將取得較好的跟蹤效果，表現(xiàn)在：由圖5可見，當(dāng)t≥tδ時，航行器可以對參考信號進(jìn)行精確跟蹤；其次，需要的控制量即推力也較小，對比圖6、圖2和圖4，可以看出，采用初始修正自適應(yīng)反演控制的控制量較非初始修正自適應(yīng)反演控制的控制量小，且不會出現(xiàn)顫振現(xiàn)象。

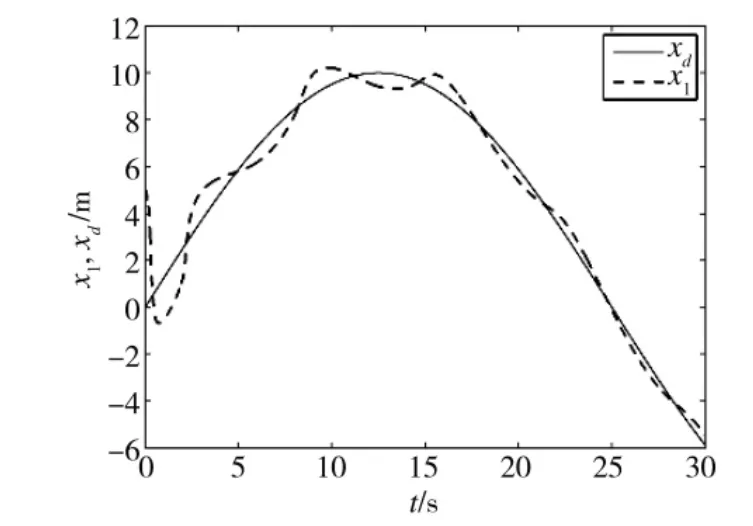
圖1 非初始修正控制下的位置跟蹤

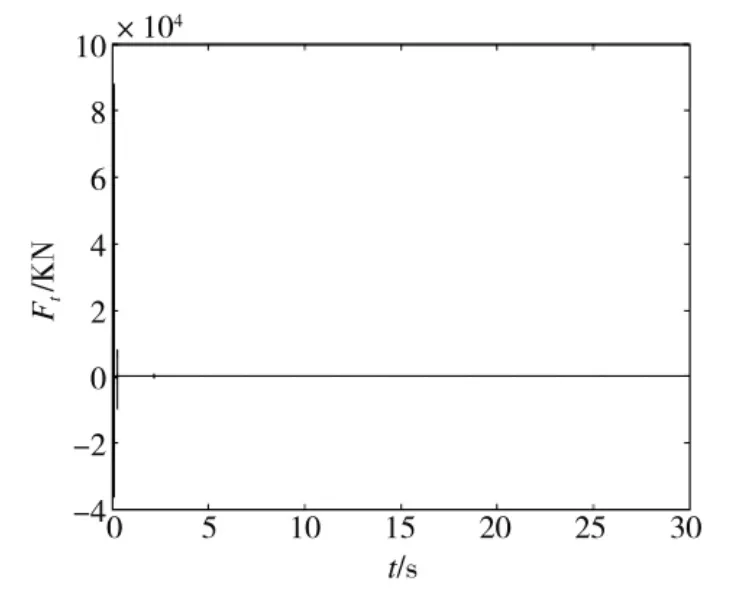
圖2 非初始修正控制下的推力

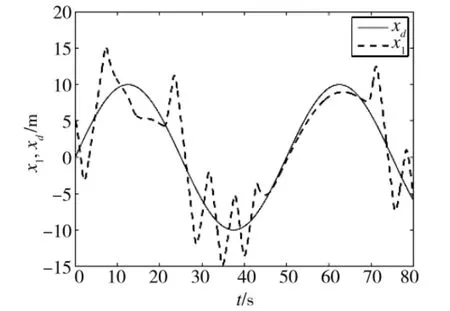
圖3 非初始修正控制下的位置跟蹤（有輸入限幅）

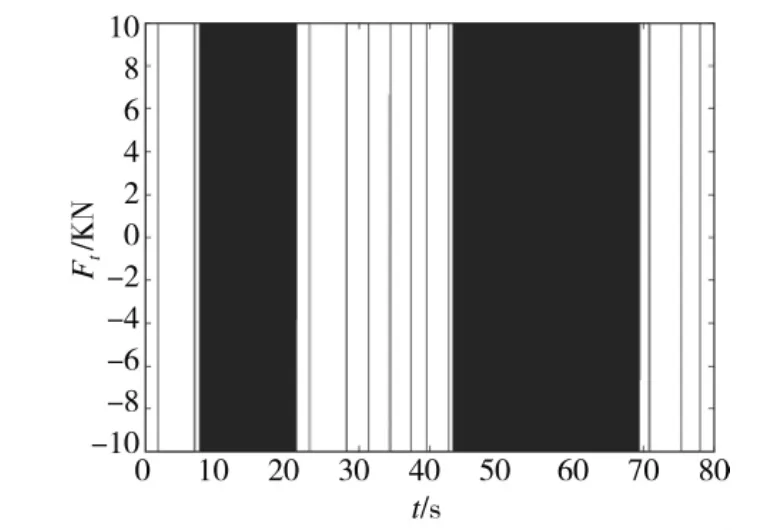
圖4 非初始修正控制下的推力（有輸入限幅）

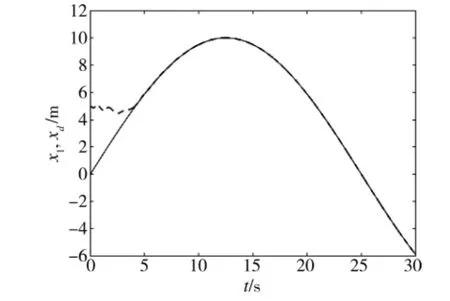
圖5 初始修正控制下的位置跟蹤

仿真對比結(jié)果表明，對于質(zhì)量較大且初始誤差也較大的水下航行器，采用本文提出的初始修正自適應(yīng)反演控制方法，可以顯著地降低實施跟蹤任務(wù)所需的期望輸出動力。

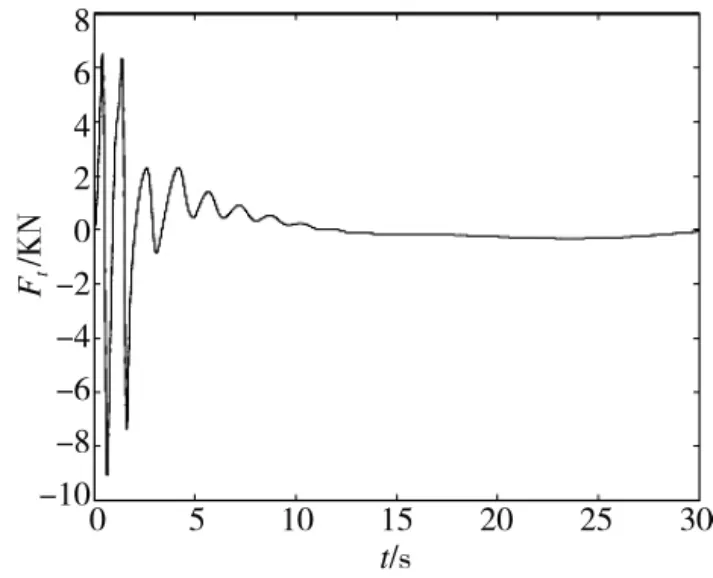
圖6 初始修正控制下的推力

5 結(jié)論

本文研究水下航行器的自適應(yīng)控制方法，首先根據(jù)傳統(tǒng)的自適應(yīng)反演控制方法，為航行器系統(tǒng)設(shè)計控制器，該方法在執(zhí)行跟蹤任務(wù)的起始階段，可能出現(xiàn)控制器所期望的推力（控制量）超過實際動力系統(tǒng)所能提供的最大推力現(xiàn)象。為改善這一矛盾，本文對前述方法進(jìn)行改進(jìn)，提出初始修正自適應(yīng)反演控制設(shè)計方法。仿真結(jié)果表明，該方法可以緩解傳統(tǒng)自適應(yīng)反演控制設(shè)計方法在實施時所需的控制量過大現(xiàn)象，并取得較好的跟蹤性能。