多粒度直覺模糊三支決策及在目標識別中應用*

范兵兵，李 進，王 毅，陳玉金

（1.空軍工程大學研究生學院，西安710051；2.西北大學信息學院，西安710051）

0 引言

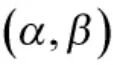
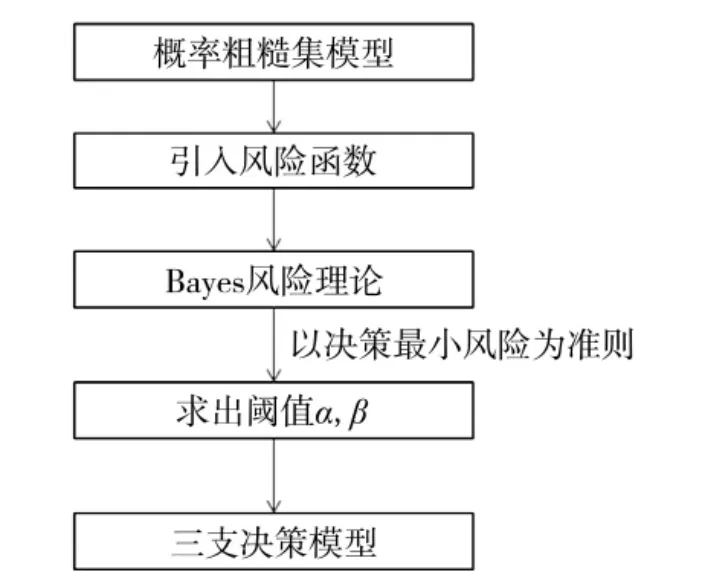
圖1 三支決策模型

由于人在決策過程中往往存在一定猶豫度，而這種三支決策模型忽略了決策過程中的猶豫度［4］，無法描述這種“非此非彼”的“模糊概念”，從而無法更加貼近實際需要，為了解決這一問題，劉盾等根據不同的需求提出了模糊三支決策、直覺模糊三支決策［5］。目前直覺模糊三支決策在構建分類器、目標識別、威脅評估［6-8］等方面的運用具有良好的效果。

粒計算［9］是當前計算智能領域最新的一種模擬人類多粒度以及分層思維來解決問題的方法，從Zadeh提出的粒計算觀點［10］來看，直覺模糊三支決策以及Yao所提出的三支決策僅僅針對于單個粒空間，而由于當前信息系統不完備性以及信息更新速度的約束，人們的認識也會隨著信息的補充從粗粒度到細粒度，因此，單個粒度空間已經不能滿足現實需要。為了模擬人類從多個粒空間描述問題的模式，錢宇華等提出了多粒度粗糙集模型［11］，多粒度三支決策正是從此發展而來，它對多粒度決策粗糙集模型進行良好的語義解釋。

基于上述發展，多粒度以及直覺模糊的思想能夠很好地優化三支決策模型，因此，本文結合多粒度三支決策以及直覺模糊三支決策，提出一種多粒度直覺模糊三支決策模型，并運用這一方法解決目標識別問題。

1 預備知識

1.1 多粒度三支決策模型

多粒度概念是粒計算理論中的核心，錢宇華、梁吉業基于多粒度的思想，將決策粗糙集中采用單個粒空間描述問題的方式拓展為采用多個粒空間描述問題的方式，提出了多粒度決策粗糙集模型，多粒度三支決策正是從此發展而來，對多粒度決策粗糙集模型進行良好的語義解釋。一般來說，多粒度三支決策模型存在兩種形式，一種稱為樂觀多粒度三支決策模型，另一種稱為悲觀多粒度三支決策模型［9］。

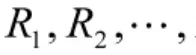
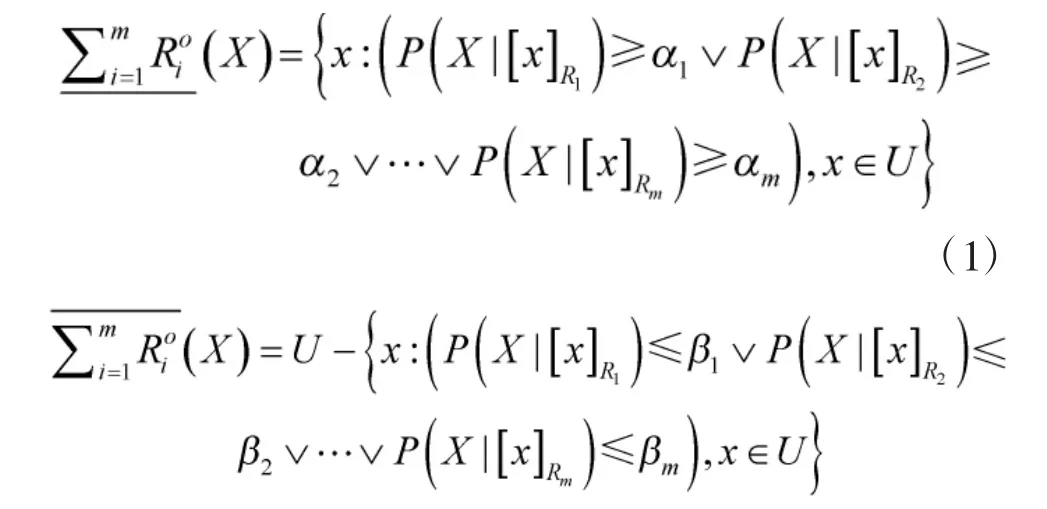
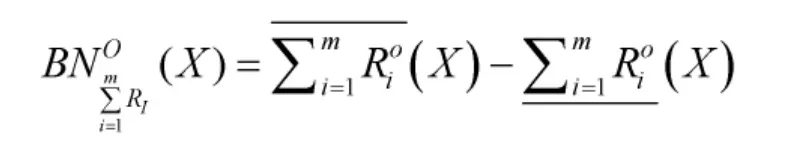
類似于經典三支決策對決策粗糙集的語義描述，樂觀多粒度三支決策模型為：

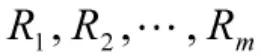
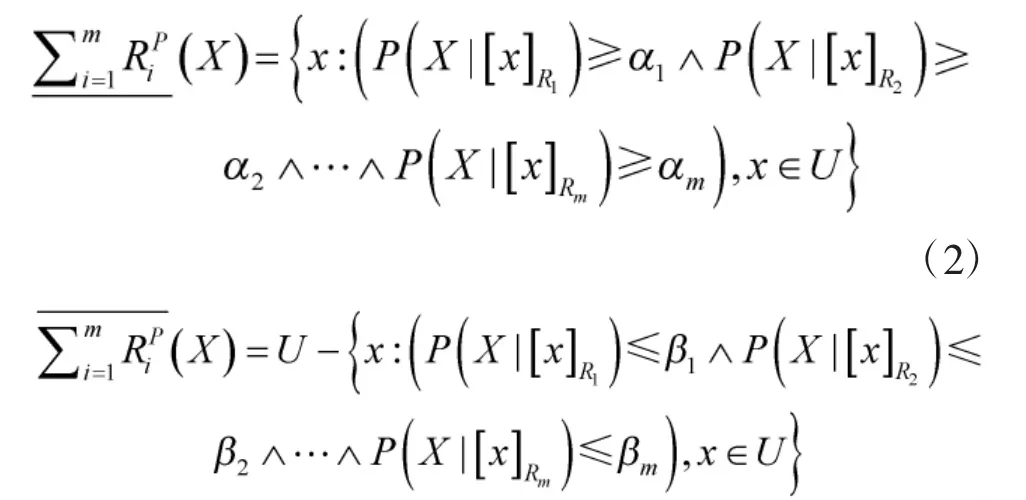
對比定義1和定義2可以得出，樂觀多粒度三支決策的正域要求至少存在一個粒空間在等價類與近似目標間的條件概率大于其相應的閾值，在決策過程中指的是：每個決策者根據自己的粒空間進行決策，而不反對其他決策者所給出的粒空間的決策，是一種“求同存異”的決策策略；悲觀多粒度三支決策的正域要求所有粒空間在等價類與近似目標間的條件概率大于其相應的閾值，在決策過程中指的是：所有的決策者使用共同滿意的方案進行決策，是一種“求同排異”的決策策略。

1.2 直覺模糊三支決策模型

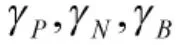
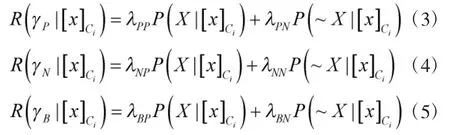
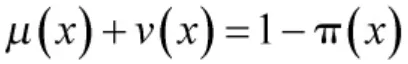
接受事件對象的期望風險：

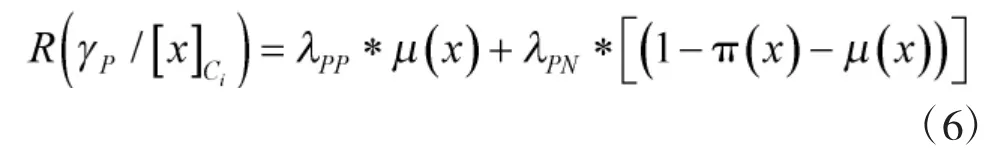
延遲決策事件對象的期望風險：

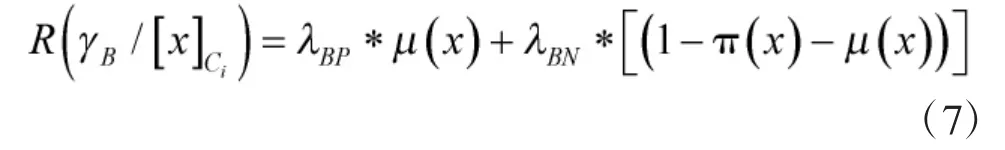
拒絕事件對象的期望風險：

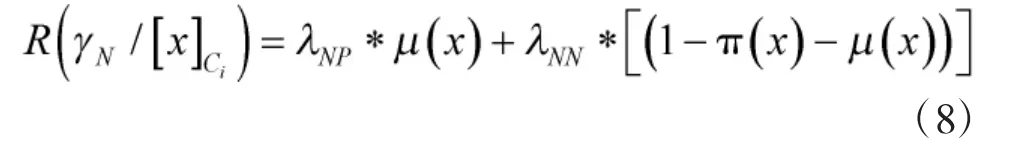
將新的期望風險代入到三支決策的三條決策規則中：

對于規則（P）：

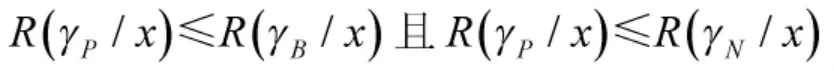
即

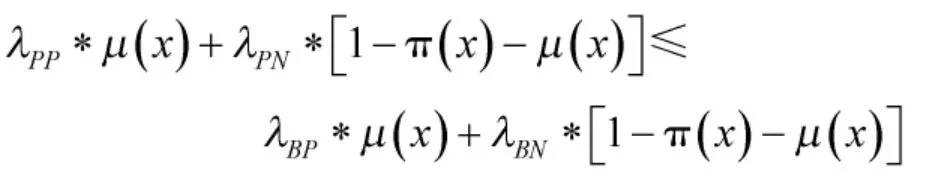
且

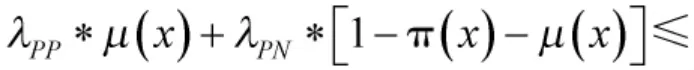
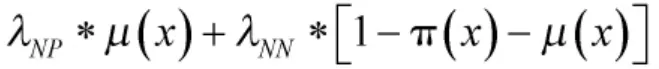
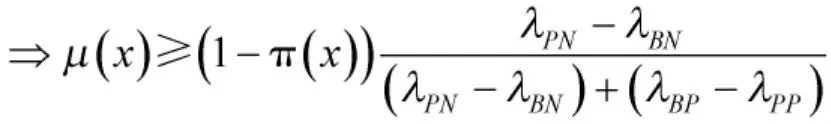
且

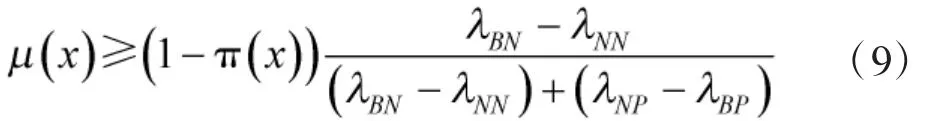
最后將規則進行改寫，得到直覺模糊三支決策模型：

2 多粒度直覺模糊三支決策

2.1 多粒度直覺模糊三支決策模型

由于多粒度三支決策與直覺模糊三支決策之間具有優勢互補的效果。一方面，多粒度理論可以擴充直覺模糊三支決策語義描述并豐富其統計特性，而不僅僅局限于單個粒度空間；另一方面，直覺模糊理論可以解決多粒度三支決策往往忽略了決策過程中人的猶豫度問題。為此本文根據技術路線圖，如下頁圖2所示。

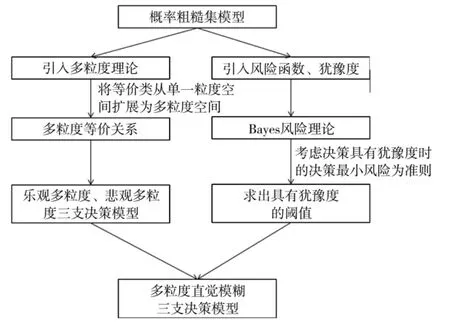
圖2 模型構建的技術路線圖

結合多粒度三支決策以及直覺模糊中的猶豫度，提出一種多粒度直覺模糊三支決策模型，該模型具有樂觀多粒度直覺模糊三支決策模型和悲觀多粒度直覺模糊三支決策模型兩種形式。

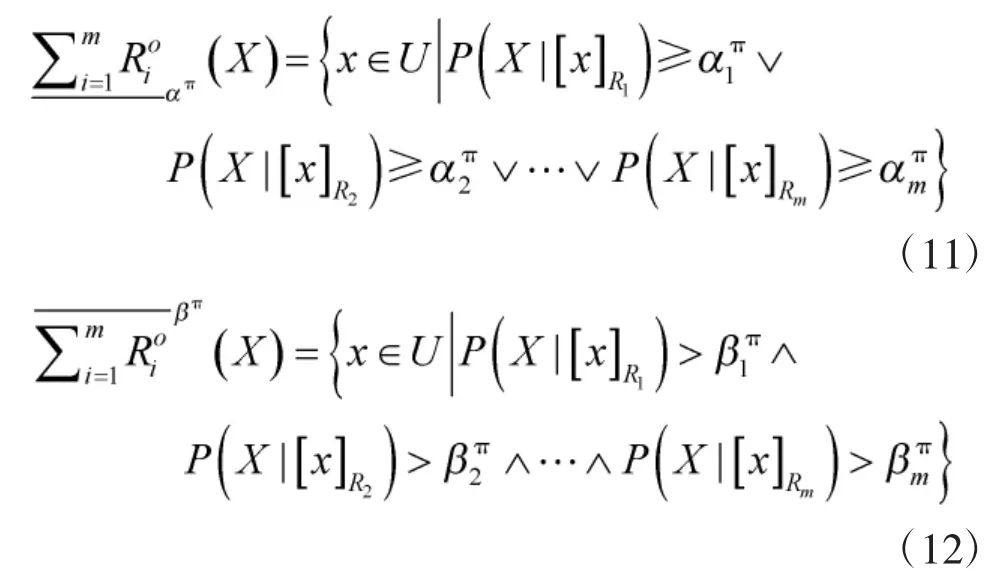
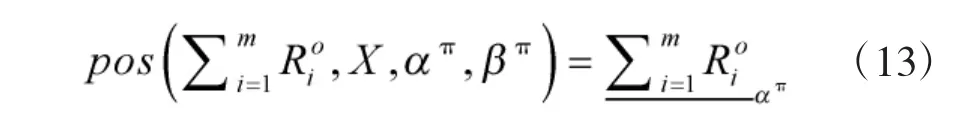
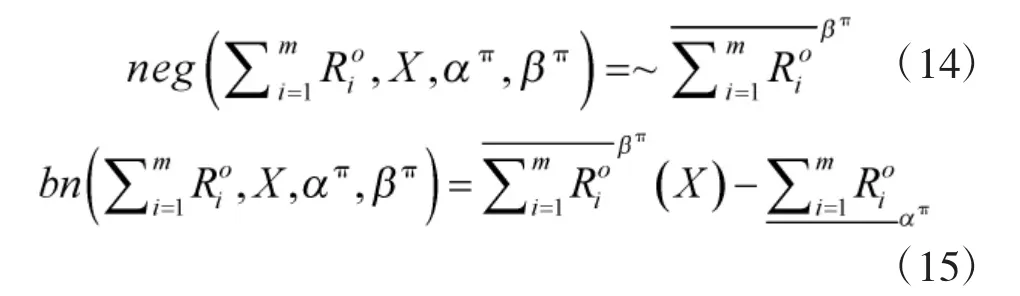
類似于經典三支決策對決策粗糙集的語義描述，樂觀多粒度直覺模糊三支決策模型為：

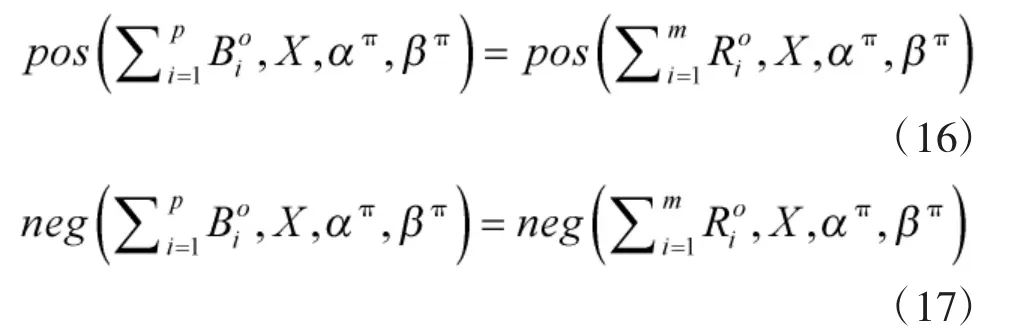
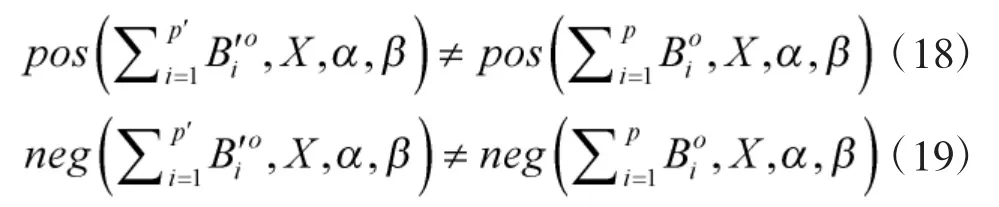
則稱A為AT的樂觀屬性約簡。

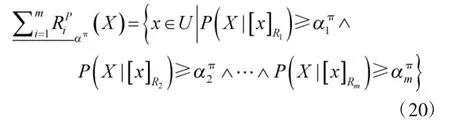
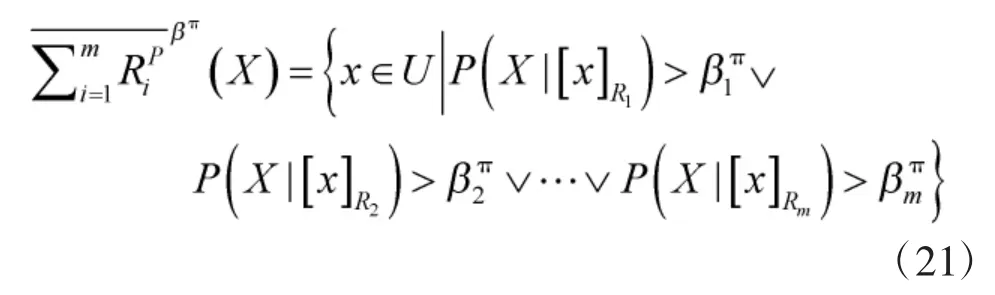
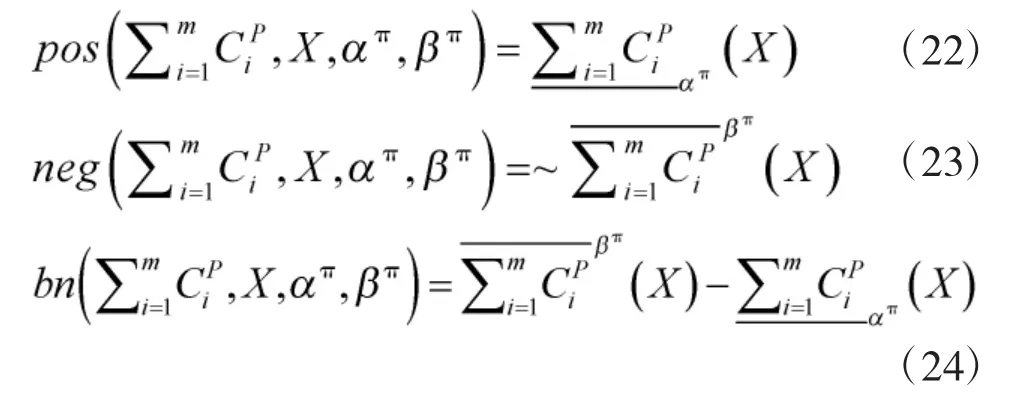
悲觀多粒度直覺模糊三支決策模型為：

從定義4和定義6中可以看出，兩種模型的上下近似算子定義中均包含了猶豫度，因此，更加符合人們的決策過程；同時兩種模型很好地保留了在多粒度空間上描述目標概念的特點，并且兩種下近似算子仍然秉持了“求同存異”、“求同排異”兩種不同的決策風格。

2.2 多粒度直覺模糊三支決策模型中閾值的確定

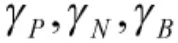
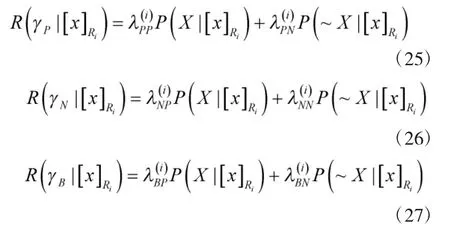
表1 初始決策規則表

對于樂觀多粒度直覺模糊三支決策模型與悲觀多粒度直覺模糊三支決策模型中的決策條件，本文根據貝葉斯最小風險決策準則，選擇風險最小的行為，最后得到決策規則如表1所示。

其中

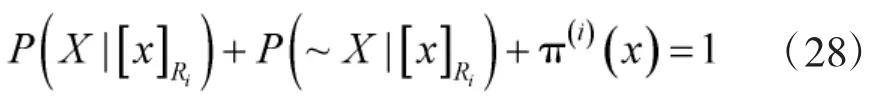
并且考慮到現實中接受正確事物的損失不大于延遲接受正確事物的損失且均小于拒絕正確事物的損失；同理，拒絕錯誤事物的損失不大于延遲拒絕錯誤事物的損失且均小于拒絕正確事物的損失。因此，

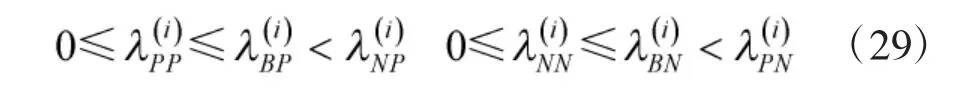
結合式（28）、式（29）將表1中決策規則P、N、B進行化簡，化簡后結果如表2所示。

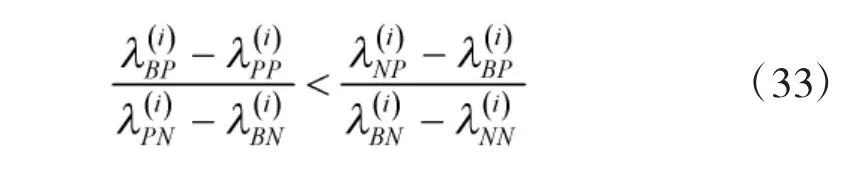
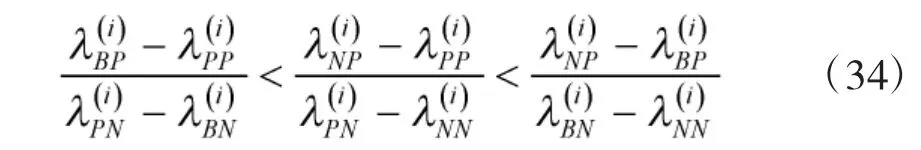
結合式（30）～式（32）對表2中決策規則P、N、B改寫，結果如下頁表3所示。

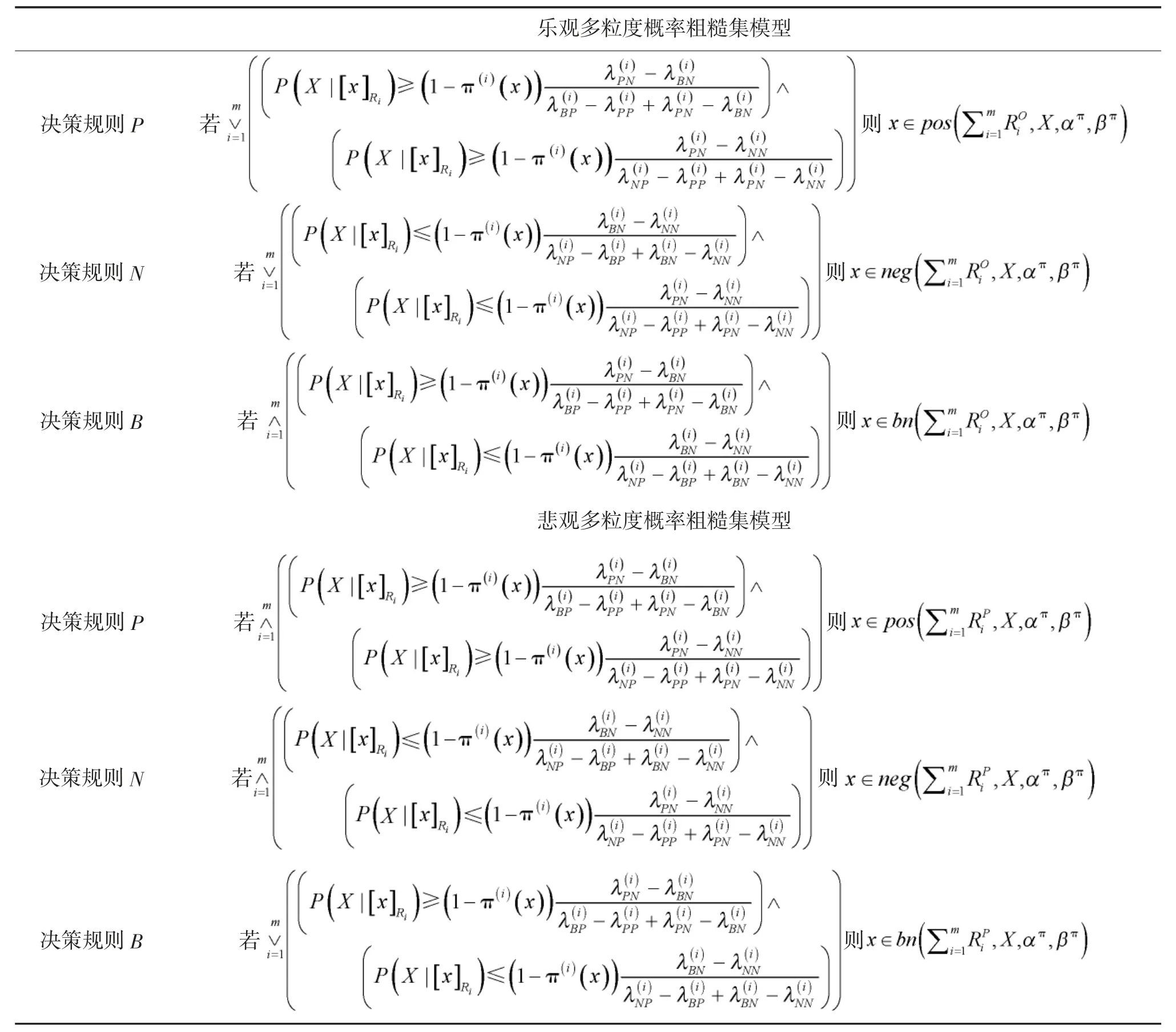
表2 化簡后決策規則

表3 改寫后決策規則表

從表3可以看出，兩種模型很好地保留了在多粒度空間上描述目標概念的特點，并且兩種模型在決策過程中仍然秉持了“求同存異”、“求同排異”兩種不同的決策風格。

3 目標識別應用實例

我方雷達在彈道導彈中段探測到10批目標的目標群，這些目標群構成論域U，如表4所示。其中，C1表示與二面角相似參數，C2表示與球體相似參數，C3表示與水平偶極子相似參數，C4表示與圓柱體相似參數，C5表示與右螺旋體相似參數，C6表示與左螺旋體相似參數。d=1表示彈頭，d=2表示誘餌。

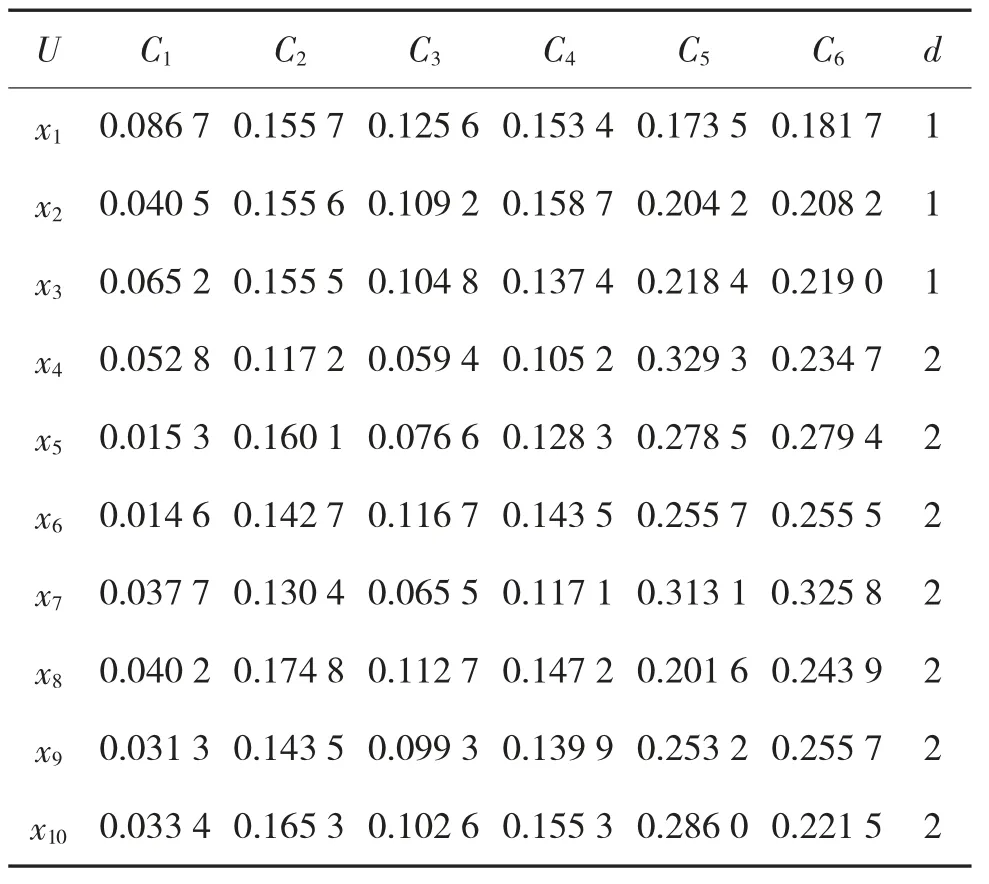
表4 目標決策信息表

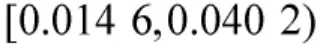
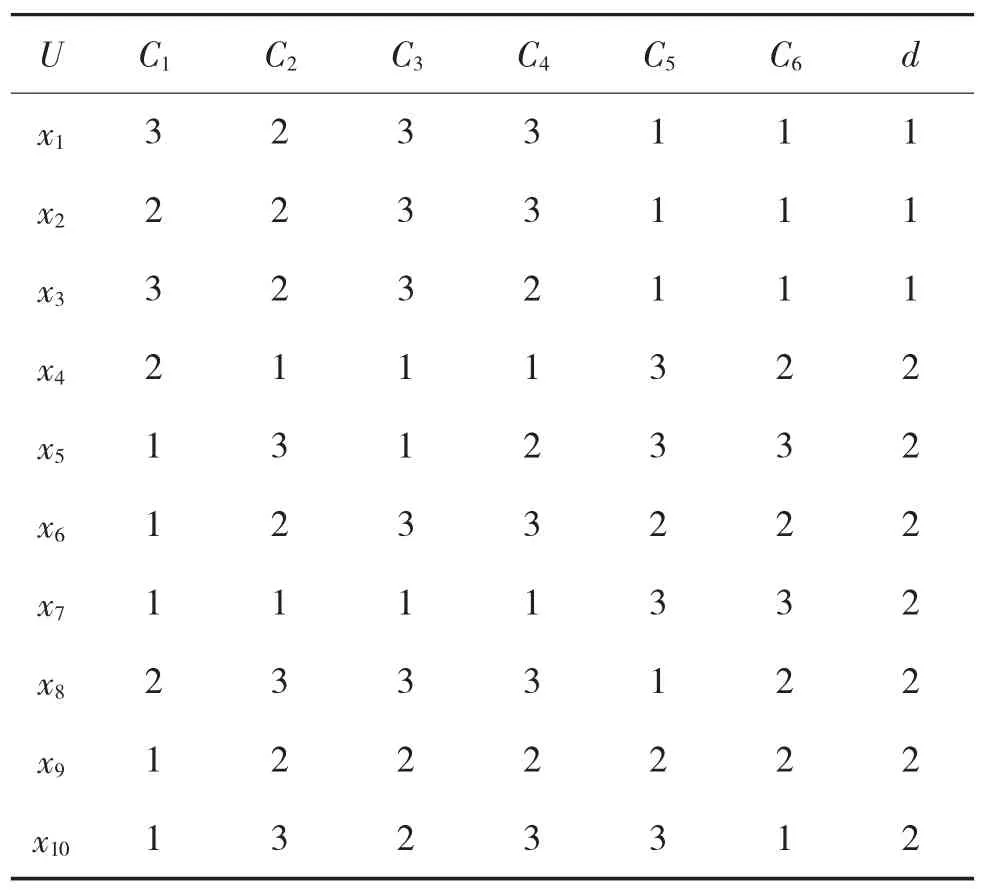
表5 離散化的目標決策信息表

在粒空間R1下劃分得到的集合為：

若取

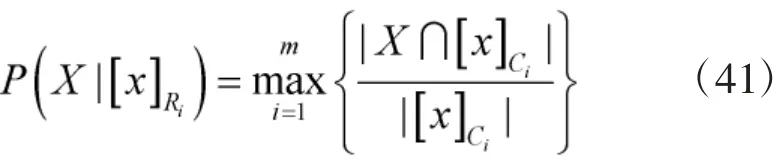
因此，樂觀多粒度直覺模糊三支決策模型劃分結果為：

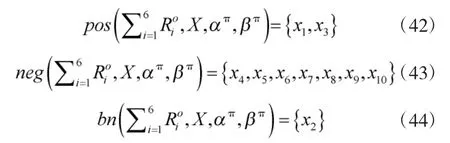
設ri為決策規則，則產生彈道導彈目標決策如表6所示：

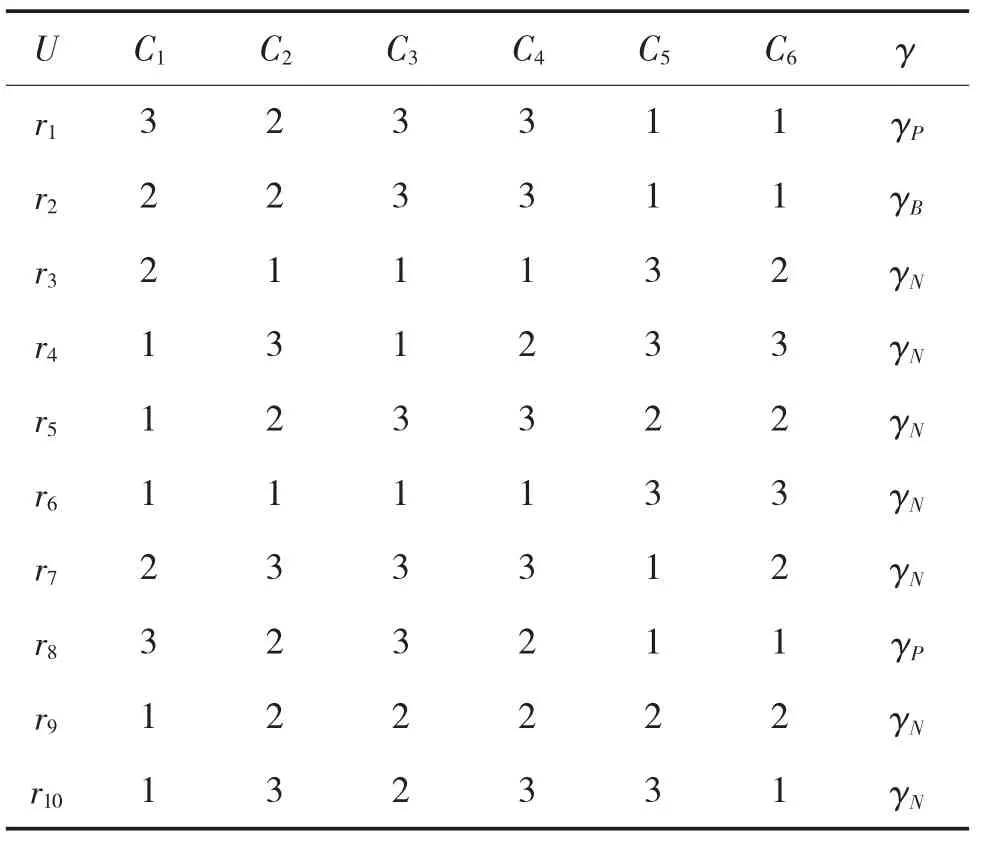
表6 彈道導彈目標決策規則表

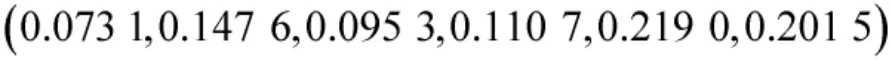
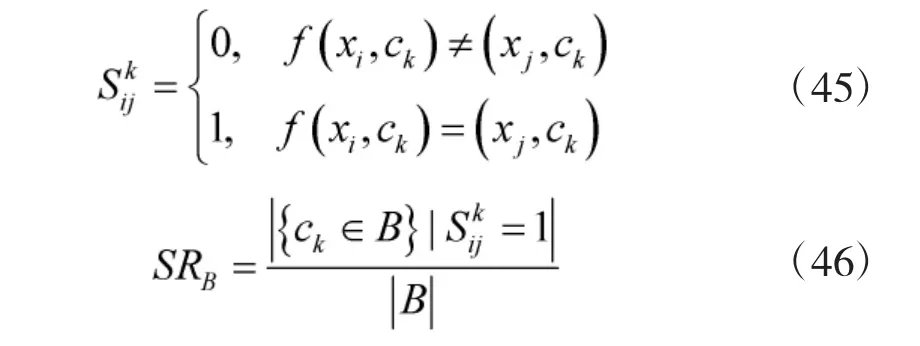
通過式（45）、式（46）計算相似率，發現與規則r1、r8進行匹配時相似率最大為2/3，因此，決定對該目標采取決策行為rp。

4 結論

多粒度直覺模糊三支決策模型從粒計算的多粒度處理問題的思想出發來描述問題，使問題能夠更加全面地展示出來；多粒度直覺模糊三支決策模型具有多粒度三支決策模型與直覺模糊三支決策模型二者優點，能夠更全面細致地反應問題。最后，利用Bayes最小風險決策理論確定樂觀多粒度直覺模糊三支決策模型和悲觀多粒度直覺模糊三支決策模型中的參數，實例證明該模型可應用于彈道導彈目標識別問題。