基于動態網格密度的SNN聚類的ET-GM-PHD濾波算法*

彭 聰，王杰貴，朱克凡

(國防科技大學電子對抗學院， 合肥 230037)

0 引言

在經典的多目標跟蹤算法中，由于雷達等傳感器分辨率較低，通常目標視為點目標進行跟蹤，此時只考慮跟蹤目標的運動信息，而未包含目標的外形信息。近年來，隨著傳感器技術的提升，運動目標在一個采樣周期里不再只返回一個量測值，這種在同一時刻能夠得到至少一個量測值的目標稱為擴展目標。擴展目標可以由運動狀態(位置、速度和加速度等)和擴展形態(大小、形狀和朝向)共同表征，擴展目標跟蹤就是基于傳感器得到的信息，利用相應的信號處理方法，對擴展目標的運動狀態和擴展形態進行精確估計的過程。

傳統的多目標跟蹤算法如聯合概率數據關聯算法、多假設跟蹤算法等都依賴于數據關聯，這類算法會帶來“組合爆炸”問題[1]，復雜的多維計算會增加算法的運行時間，影響跟蹤性能。基于隨機有限集的多目標跟蹤算法規避了數據關聯，有效的解決了“組合爆炸”問題。隨機集理論是Matheron于上世紀七十年代提出的，主要應用于幾何方面，在上述基礎上， Mahler提出了有限集統計特性理論，它是隨機集的一種特例，將隨機變量的統計理論延伸到了隨機集合(random finite set, RFS)，并率先將RFS理論應用于多目標跟蹤領域。RFS框架下的多目標跟蹤利用Bayes法則傳遞目標的概率密度，但是算法中的積分為集值積分，很難求解。做為一種近似的濾波方法，概率假設密度(probability hypothesized density, PHD)濾波器被提出來，它傳遞的目標概率密度的一階統計近似矩。2009年，Mahler將PHD濾波技術應用于擴展目標領域，并給出了擴展目標PHD(extended target PHD, ET-PHD)濾波器的更新方程[2]。2010年，Granstrom等學者給出了ET-PHD的高斯混合實現形式，即ET-GM-PHD濾波[3]。

擴展目標跟蹤面臨的首要問題就是量測集的劃分，文獻[4]中提出了一種基于距離的劃分方法，該方法對空間上距離較遠且量測比較密集的情況跟蹤效果較好；文獻[5]提出k-means劃分方法，其劃分準確度好于距離劃分，但是本質上，以上兩種劃分方法都是基于距離劃分的，在量測密度差距較大的環境下，兩者劃分效果不理想。針對此問題，文獻[6]提出了一種基于SNN相似度的量測劃分方法，該方法對量測密度不敏感，但存在計算量偏大的不足。

本文在文獻[6]的基礎上，提出了基于動態網格密度的SNN相似度劃分算法，該算法首先通過動態網格計算量測集的密度分布情況，利用雙閾值對量測集進行雜波濾除；然后根據SNN相似度對處理后的觀測數據進行劃分，以達到節省計算時間，提高跟蹤穩定性的目的。

1 ET-GM-PHD濾波技術

1.1 ET-PHD濾波技術

ET-PHD濾波算法的預測步和標準的PHD濾波算法預測步一致，其更新方程是預測強度vk|k-1(x)和一個量測偽似然函數LZ(x)的乘積形式，下面給出ET-PHD濾波算法的具體形式[7]。

1)預測部分

設k-1時刻的后驗強度為vk-1，則ET-PHD預測強度為：

βk|k-1(xk|xk-1)]vk-1(xk-1)dxk-1

(1)

式中：γk(xk)表示k時刻新生目標的RFS的強度函數；pS,k(xk-1)為目標在k時刻存活的概率；fk|k-1(xk|xk-1)為k時刻單目標的轉移概率密度；βk|k-1(xk|xk-1)表示衍生目標的強度。

2)更新部分

假設k時刻的預測強度vk|k-1(x)和量測集Zk，且量測個數服從Poisson分布，ET-PHD更新方程為：

vk(x)=LZ(x)vk|k-1(x)

(2)

LZ(x)是量測的偽似然函數：

LZ(x)=1-(1-e-γ(x))pD(x)+

(3)

式中:γ(·)表示擴展目標所產生的量測值的均值；pD(·)為目標被檢測概率；p∠Zk表示p為量測集合Zk的一個劃分子集；ωp為劃分p的權值；|W|為子集W內元素的個數；dW為觀測子集W的非負系數；φz(x)為擴展目標量測的似然函數；λk為單位空間內的雜波個數；ck(zk)為雜波的分布函[8]。

1.2 ET-GM-PHD濾波技術

由于ET-GM-PHD濾波算法和標準的GM-PHD濾波算法的預測步和更新步一致，因此文中只給出標準GM-PHD濾波算法的預測和更新方程。

GM-PHD濾波器滿足以下假設條件:

1)每個目標的運動模型和量測模型均為高斯線性的，即：

fk|k-1(x|xk-1)=N(x;Fk-1xk-1,Qk-1)

(4)

gk(z|x)=N(z;Hkxk,Rk)

(5)

2)目標的生存概率和檢測概率與目標狀態相互獨立，即：

pS,k(x)=pS,k

(6)

pD,k(x)=pD,k

(7)

(3)新生目標的RFS強度為高斯混合形式，即：

(8)

基于以上假設，GM-PHD濾波器的預測步可表示為：

(9)

更新步可表示為：

(10)

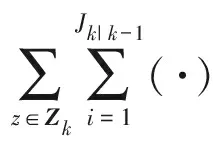
1.3 擴展目標量測劃分問題

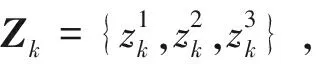
從上述例子可見，量測值的增加將使得量測集的劃分數迅速增加，影響跟蹤的實時性，因此尋找準確快速的量測劃分方法是ET-GM-PHD濾波中的重要一步。針對這個問題，提出了基于動態網格密度的SNN相似度的量測劃分算法。

2 基于動態網格密度的SNN相似度量測劃分方法

在SNN算法的基礎上，利用動態網格技術對量測數據進行預處理，從而達到減小算法運行時間，提高跟蹤精度的效果。

2.1 基于動態網格密度的量測集預處理

定義1：網格單元：數據空間中的每一維均勻的分成若干等分，從而將數據空間劃分成若干個互不相交的超矩形單元，這樣的單元稱為網格單元。采用動態網格劃分，根據每一時刻數據點的數量來決定網格的劃分數[9]：

K=(Nz,k(1-γ))1/d

(11)

式中:Nz,k表示k時刻量測集的個數z，γ表示數據壓縮率，d表示數據的維數。

定義2：網格單元的中心與重心。設一個網格中有m個數據點b1,b2,…,bm，該單元的中心點Uc是一個d維的向量(uc1,uc2,…,ucd),uci=(li+hi)/2,li和hi分別表示網格單元第i維的最小值和最大值；重心點Ub是一個d維的向量(ub1,ub2,…,ubd)，ubi=(b1i+b2i+…+bmi)/m。

定義3：網格單元密度。網格單元中數據點的個數用den(C)表示。

2.1.1 改進的密度閾值的選取

密度閾值的選取是區分量測和雜波的關鍵，在利用式(11)對數據空間進行動態網格劃分后，選擇合適的密度閾值，對量測劃分結果的影響很大。傳統的方法中主要利用單密度閾值來判斷高低密度網格，該方法具有明顯的不足：密度閾值選取偏大時，會將量測和雜波一同濾除；密度閾值選取偏小時，則會認定雜波為量測。鑒于此，文中借鑒平均密度的思想，采用雙密度閾值對量測和雜波進行區分，在原有密度閾值的基礎上，添加一個核心密度閾值[10]。

假設G為生成的網格數量，den(Ci)為網格單元密度，max(den(Ci))表示密度最大的網格單元，min(den(Ci))表示密度最小的網格單元，有如下定義，密度閾值ε：

(12)

核心密度閾值ε′：

(13)

定義den(Ci)≥ε′的網格為核心網格，den(Ci)≥ε的網格為高密度網格，den(Ci)≤ε的網格為低密度網格，核心網格也是高密度網格。在濾除雜波的過程中，將含有核心網格的高密度網格區域認定為量測，不包含核心網格的高密度網格區域和低密度網格區域認定為雜波[11]。

2.1.2 移動網格邊界優化技術

為了使量測值和雜波劃分結果更準確，需要對邊界信息進行處理。問題描述如圖1(a)，單元中C點和B點同屬于量測值，但由于密度閾值的設置，處于低密度網格中的C點將被當作雜波被濾除。為了避免這種情況發生，文中采用移動網格邊界優化技術[12]，對低密度網格以及不含核心密度的高密度區域中的數據點進行處理。掃描需要處理的網格中的數據點，以網格重心為中心，依據式(11)劃分的網格邊長建立新的網格，若新建網格的密度den(Cj)≥ε′，則保留網格中的數據點，將其歸為量測值。如圖1(b)中所示，以C點為中心建立新的網格，此時den(Cj)≥ε′，故將C認定為量測，避免了上述問題中將邊界量測點C歸為雜波的情況。為了保證算法的運行效率，移動網格邊界優化步驟只執行一次。

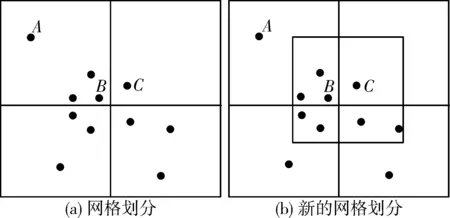
圖1 移動網格邊界優化

2.1.3 雜波濾除預處理

基于動態網格密度量測集預處理的步驟如下：

步驟2:將全部數據映射到已劃分的網格單元中，計算網格的密度；

步驟3:根據式(12)、式(13)得到的密度閾值和核心密度閾值對網格進行雜波濾除；

步驟4:利用移動網格邊界優化技術，對邊界值進行提取，保留符合要求的邊界值。

為驗證動態網格雜波剔除效果，進行了雜波濾除仿真實驗，圖2是在γ=0.5的情況下得到的雜波剔除仿真圖。圖2(a)是量測圖，有3個高密度區域為量測點集合；圖2(b)是經過雙密度閾值濾波后得到的效果圖，從圖中可以看到，由于右下角量測集網格密度小于核心密度，被視為雜波剔除了；圖2(c)是經過移動網格邊界優化技術處理后的仿真圖，原來被視為雜波處理的量測集經過移動網格邊界優化后，重新被認定為量測值。經過動態網格濾波后，雜波占比由原來的37.7%降低至8.1%，雜波剔除效果比較明顯。

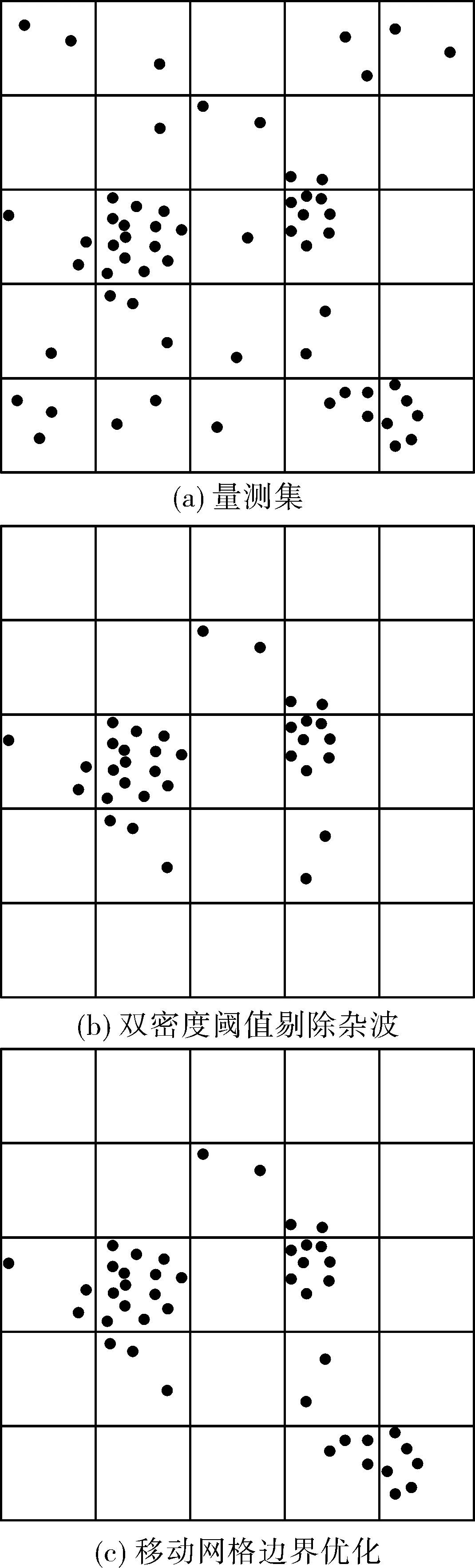
圖2 動態網格雜波剔除

2.2 基于SNN相似度的量測劃分算法

2.2.1 SNN相似度

針對不同擴展目標產生量測密度差異較大的情況，引入共享最近鄰(SNN)相似度的概念，以SNN相似度為劃分指標，對擴展目標量測集進行量測劃分。

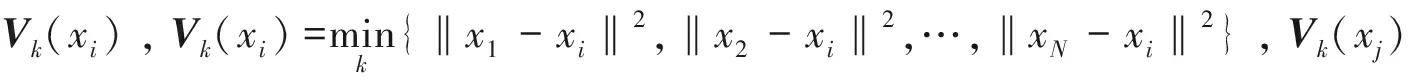
各詩家的詩選本無疑都蘊含著自己的詩學理想和個人偏向，沈德潛選詩自然也不例外。沈德潛作詩主張“格調說”，“格調說”由明前后七子提倡，在當時及清初都備受批判，沈德潛重新關注并發揚光大，成為了影響世人創作的重要思想主張。“格調說”提倡“格高調響”，在創作上提倡發揚詩教傳統，對“溫柔敦厚”“教化人倫”“合乎風雅”之詩格外看重。《別裁》作為沈德潛的代表作，必然浸潤著“格調說”的種種主張。在初刊本的序中，沈德潛提到了詩選本的重要性：

簡而言之，當兩個量測點共同包含一定數目的最近鄰點時，則認定這兩個量測點相似。

SNN相似度劃分算法中需要對K值進行設定，K值的設定范圍是依據實驗結果統計得到的，文中采用文獻[4]的統計結果，如表1所示：

表1 參數K的設定范圍

SNN相似度的具體計算步驟如下：

初始化k；

令Xun=X；

計算數據集X的距離矩陣；

IfXun≠?，則

{任意選擇一個x∈Xun;

計算x的k-鄰域Vk(x)={x1,x2,…,xk},

其中x1,x2,…,xk是x的k-鄰域中的數據點

Fori=1,i≤k

{ifx∈Vk(xi) 則

SNN(x,xi)=Vk(x)∩Vk(xi);

else SNN(x,xi)=?;}

Xun=Xun-Vk(x);}

End If

2.2.2 基于SNN相似度的劃分算法具體實現步驟

SNN相似度代表了兩量測點的k-鄰域之間共同量測點的個數，基于SNN相似度的量測集劃分方法將SNN相似度大于一定相似度閾值sl的量測歸于同一簇中，實現步驟如下：

步驟1：量測集經過預處理后，統計量測集內每兩個量測點之間的歐式距離；

步驟2：根據步驟1得到的統計結果，找到每個量測值的K個最近鄰點，計算每兩個量測點之間的SNN相似度；

步驟3：根據SNN相似度，建立n維的SNN相似度矩陣N，n為量測點的個數，如圖3所示。

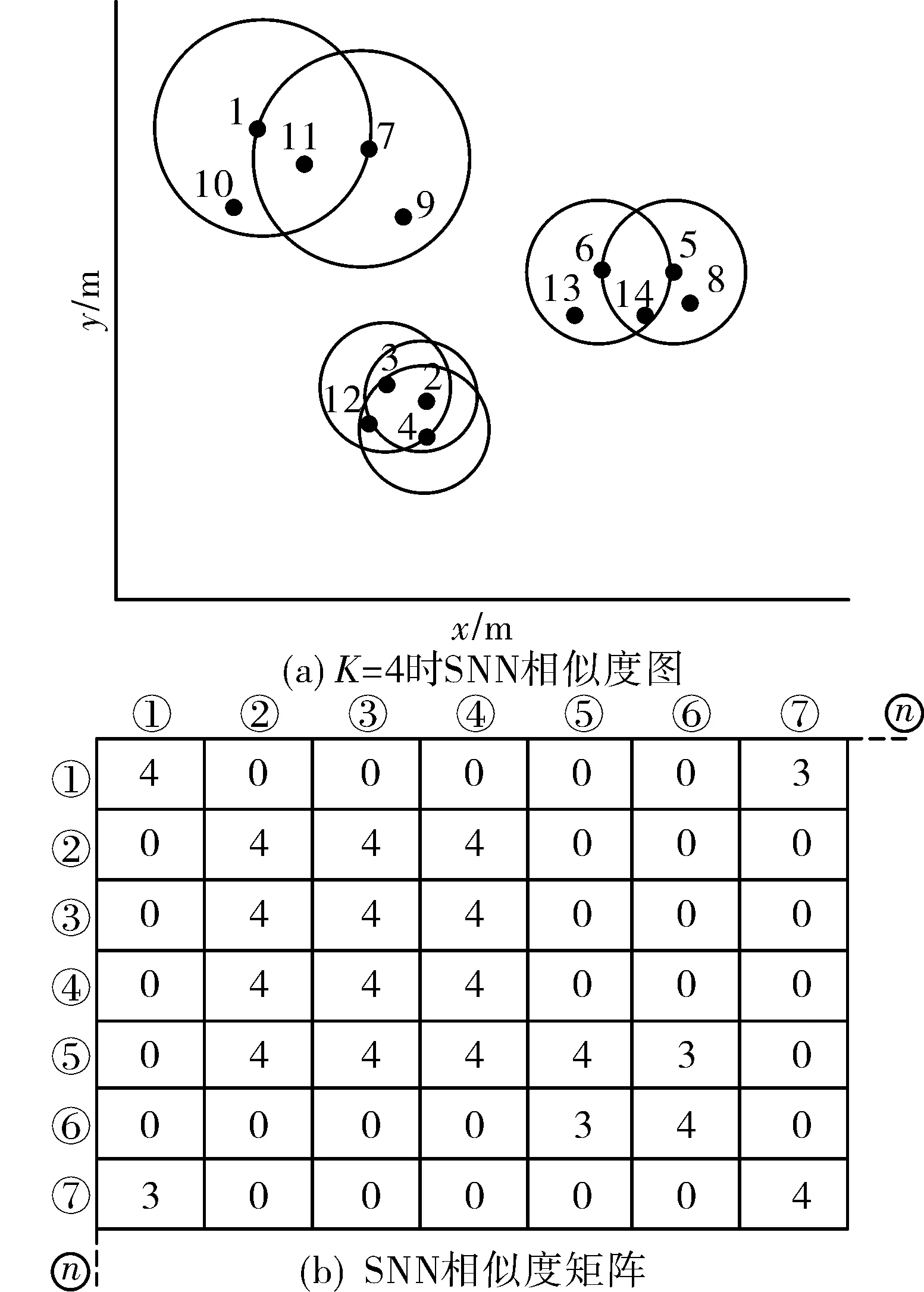
圖3 構建SNN相似度矩陣

步驟4：選擇相似度閾值sl，sl從0到K-1內選取，選取不同的閾值sl得到不同的劃分結果，共K種劃分結果。文中未討論如何選取sl得到正確的劃分結果，根據實驗仿真劃分統計結果，選取K/2作為相似度閾值sl。

步驟5：保留≥sl的SNN相似度，用1表示，其余的用0表示，形成矩陣Sth，對于圖2(b)，選取sl=2，可表示為圖4，將矩陣Sth中同一個的1連通域對應的量測置于同一個簇，連通域的個數即為簇的個數。

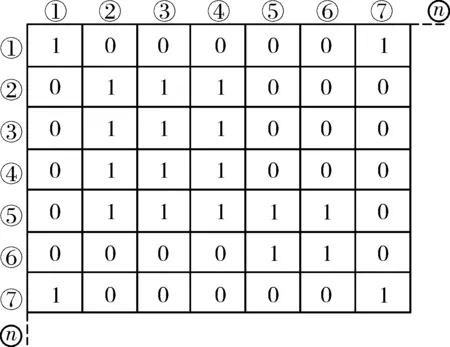
圖4 SNN相似度矩陣Sth

圖5分別是采用k-means算法和基于SNN相似度劃分算法的結果。從圖5(a)中可以看到，k-means算法將目標1劃分成了兩個簇，并且和目標2混淆了；圖5(b)是基于SNN相似度劃分的劃分結果，與正確的劃分結果一致，參數K=6，sl=3。

圖5 k-means劃分和SNN相似度劃分效果圖

3 仿真實驗與分析

文中采用ET-GM-PHD濾波器，對量測密度相差較大的幾個擴展目標進行跟蹤，對提出的基于動態網格密度的SNN相似度劃分算法和傳統的k-means劃分算法進行跟蹤性能的比較。

3.1 仿真場景設置

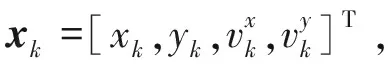
(14)

擴展目標的量測方程可表示為：

(15)

式中：量測噪聲vk是均值為0，協方差Rk=(20 m/s)2I2的高斯白噪聲，且目標產生的量測互不相關。

3.2 仿真結果分析

為了驗證文中提出的算法的特性，本次實驗進行100次蒙特卡洛仿真，和傳統的基于k-means劃分的多擴展目標PHD濾波進行對比，PHD濾波器采用高斯混合的實現形式。仿真結果如下。

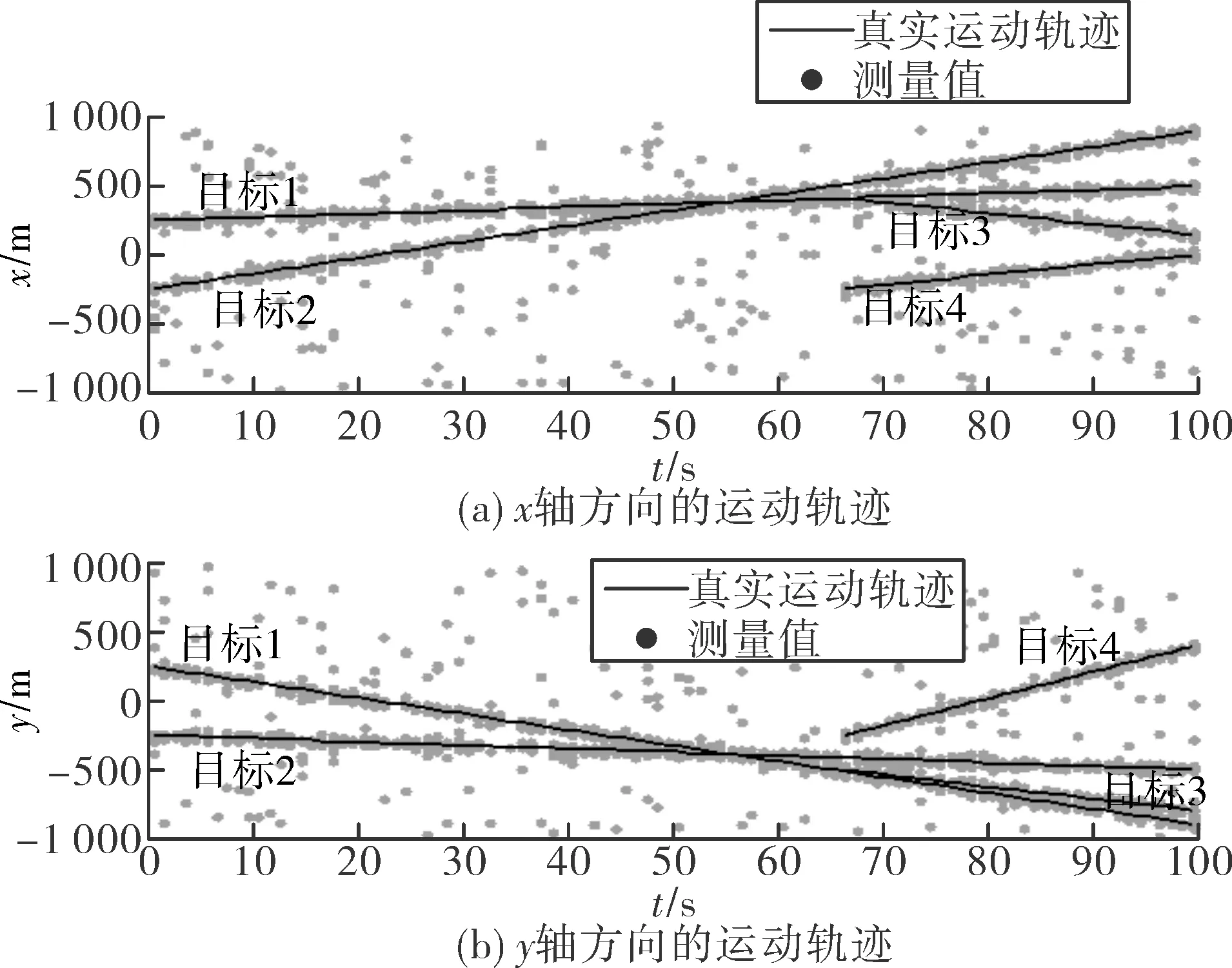
圖6 目標和雜波態勢圖

圖6顯示的是目標和雜波的態勢圖，目標產生量測個數和雜波個數均服從泊松分布，仿真場景中共4個目標，目標1，2的量測密度服從λ=10的泊松分布，目標3，4的量測密度服從λ=30的泊松分布，目標初始狀態和始末時間如表2所示，雜波個數服從λ=10的泊松分布。

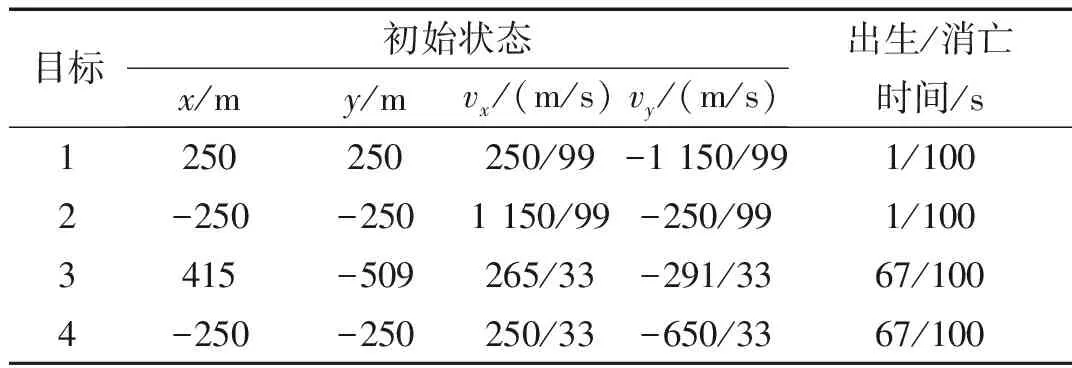
表2 目標初始狀態和始末時間

圖7給出了兩種算法的平均運行時間，從圖中可以看出，相較于傳統的基于k-means劃分的PHD算法，文中提出的算法在運行時間上減少了30%～40%，這是因為在量測劃分階段前進行了動態密度網格濾波，將大量的雜波剔除，減少了計算機對雜波的無效計算時間。

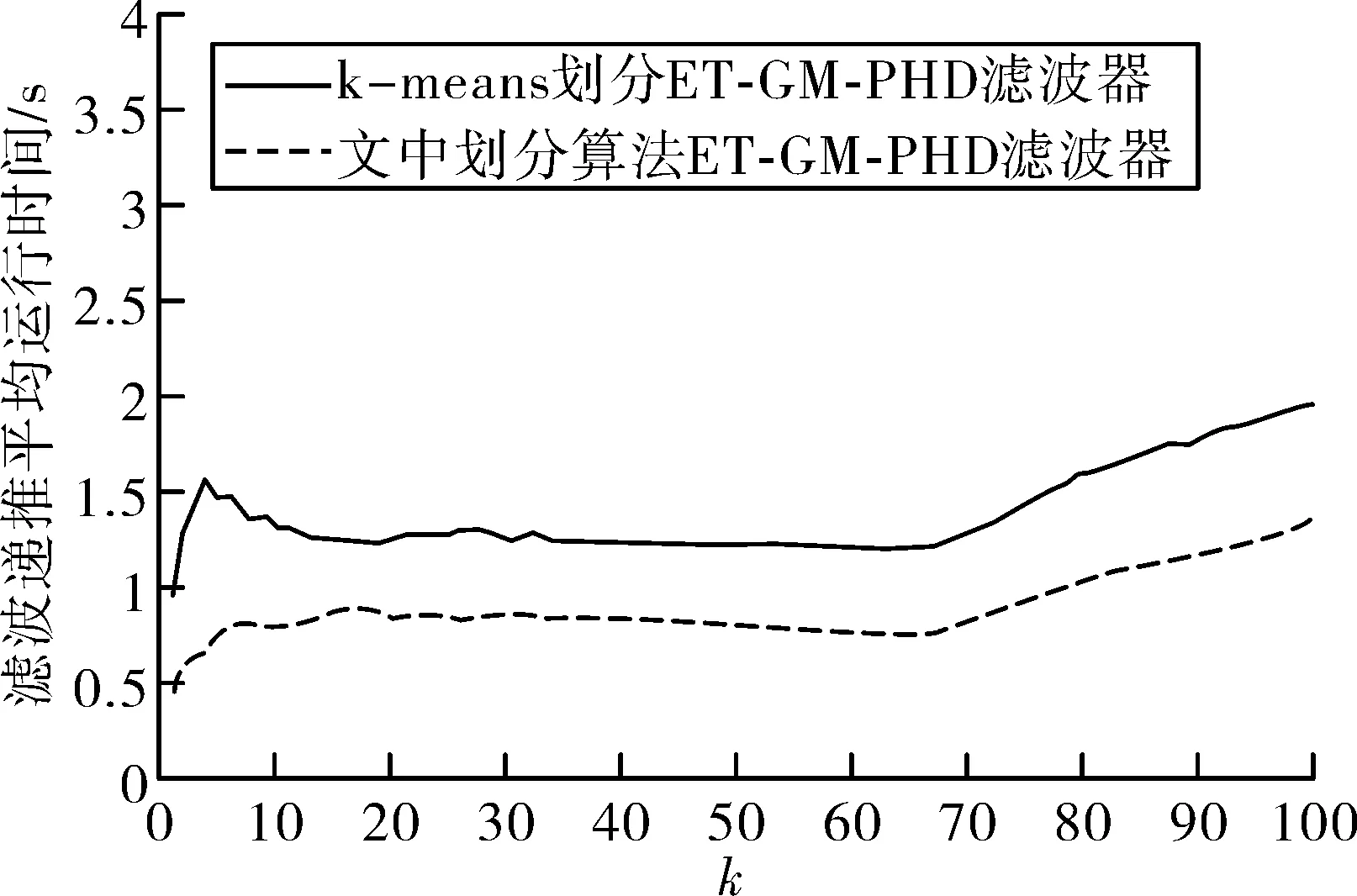
圖7 算法平均運行時間

圖8是兩種算法對目標數估計的仿真圖。如圖中所示，兩種算法在目標交叉，產生新生目標和衍生目標時都會發生目標個數的錯誤估計，但是文中算法發生誤判的時間較短，這是因為基于SNN相似度的劃分算法不再以距離為聚類標準，對于本實驗中密度相差較大的量測集的劃分效果要比k-means算法好，只有在目標極為接近時，才會導致本算法錯誤劃分量測集。

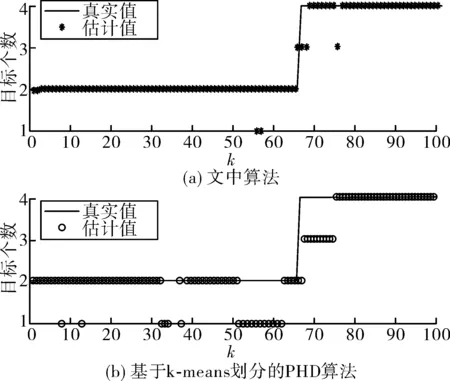
圖8 目標估計個數比較

圖9給出了兩種算法的OSPA距離圖，OSPA距離[15]是隨機有限集框架下的多目標跟蹤算法的性能評價指標,公式定義如下：

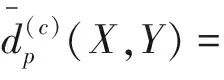
(16)

c為勢誤差與狀態誤差調節因子，p決定了對異常值的敏感性。本實驗中c=10，p=2。如圖9(b)所示，本算法的OSPA距離僅在56 s，67 s，77 s時刻左右出現了較大波動，波動時間較短，而傳統算法的OSPA距離波動次數較多，持續時間較長，這說明文中所提出的算法在對多擴展目標進行跟蹤時，有較好的穩定性。圖中出現較大波動均是在目標數目估計出現誤差的情況下發生的，因此OSPA曲線也可以反應目標數目的變化。

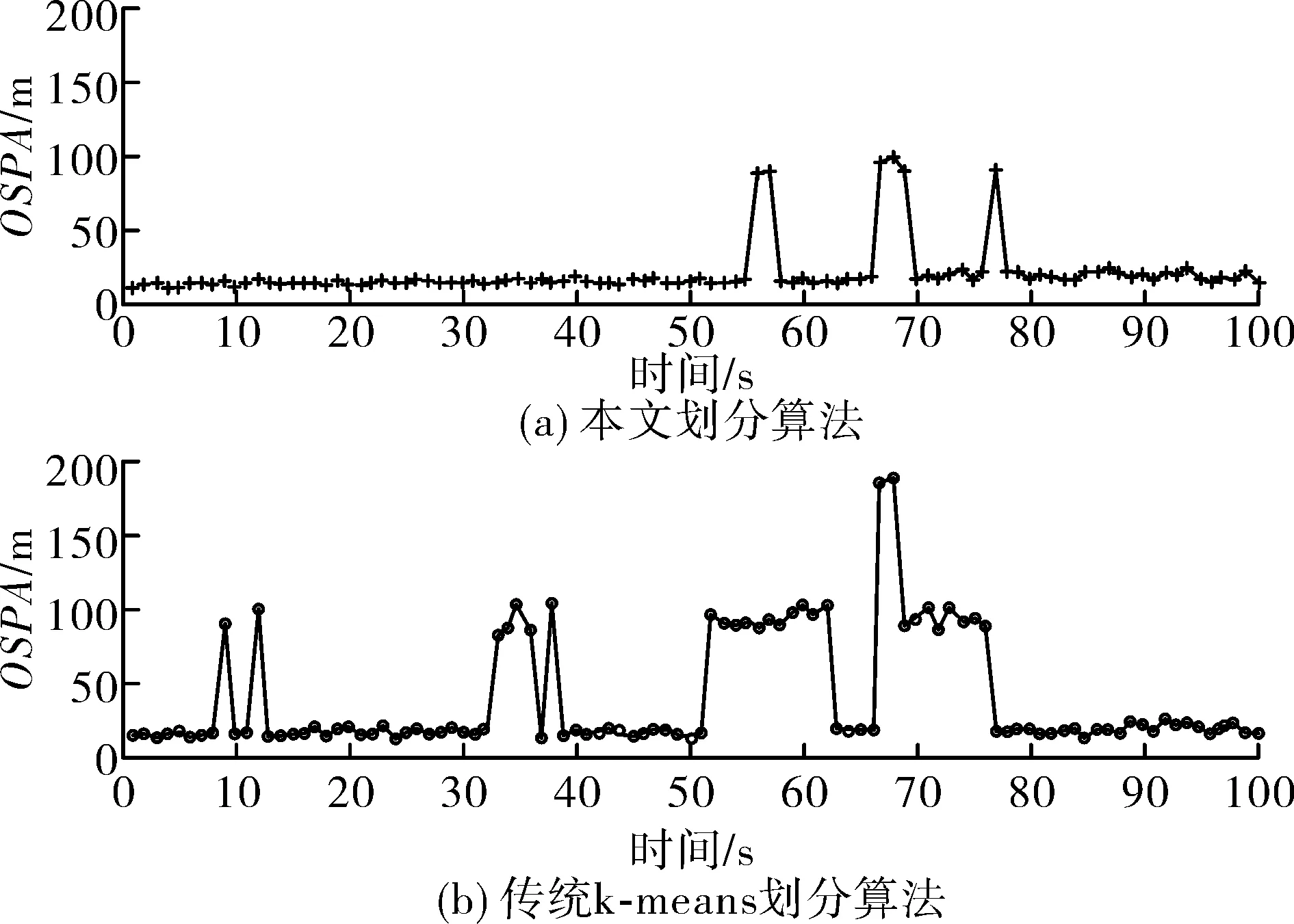
圖9 兩種算法OSPA比較

綜上所述，文中提出的算法在對量測密度差異較大的擴展目標跟蹤時，所用時間節省了30%～40%，跟蹤穩定性也好于傳統算法。

4 結束語

針對擴展目標產生量測密度差異較大的情況，文中提出了一種基于動態網格密度的SNN相似度的劃分算法，對比于傳統的劃分算法，文中算法在降低計算時間的同時，保證了跟蹤過程的穩定性和精確性，為擴展目標PHD濾波算法提供了一種新的劃分方法。下一步將對算法中參數sl的選擇問題進行研究。