高斯過程回歸下的擴展目標(biāo)高斯粒子濾波算法*

遲珞珈，馮新喜，王 泉

(空軍工程大學(xué)信息與導(dǎo)航學(xué)院，西安 710077)

0 引言

在擴展目標(biāo)跟蹤問題中，目標(biāo)已經(jīng)不能簡單地由一個點表示，而需要從量測集中獲得一個擴展形態(tài)。目標(biāo)的擴展形態(tài)可以建模為圓形、矩形、橢圓形、星凸形等一些幾何形狀。2008年，Koch首次提出隨機矩陣法[1]，將目標(biāo)建模為橢圓形，并對目標(biāo)的運動狀態(tài)和擴展形態(tài)進行估計。2012年，Granstrom[2]將隨機矩陣運用于擴展目標(biāo)PHD濾波器中, 提出Gaussian inverse Wishart PHD 濾波器, 隨后又將其運用于CPHD 濾波器, 推導(dǎo)出了Gamma Gaussian inverse Wishart PHD 濾波器[3]。 2008年,Baum提出了基于隨機超曲面的擴展目標(biāo)跟蹤方法[4]。在此基礎(chǔ)上，Baum又將目標(biāo)建模為星凸模型[5]，實現(xiàn)了對形狀不規(guī)則目標(biāo)的跟蹤。2014 年 ，Lan Jian使用多個橢圓的組合對擴展目標(biāo)進行建模[6]，提高了對目標(biāo)外形估計的準(zhǔn)確性。2015年，Wahlstr?m提出采用機器學(xué)習(xí)中的高斯過程回歸來估計目標(biāo)擴展外形[7]，避免了之前算法中由于參數(shù)過多導(dǎo)致計算復(fù)雜的問題，同時實現(xiàn)了對任意未知外形目標(biāo)的精確估計。但由于該算法使用擴展卡爾曼濾波(EKF)對運動狀態(tài)進行估計，因此存在跟蹤穩(wěn)定性差的情況。

針對上述問題，基于高斯粒子濾波器魯棒性強，較好解決粒子退化的特性，文中提出一種高斯過程回歸下的星凸型擴展目標(biāo)高斯粒子濾波算法。該算法提高了目標(biāo)跟蹤的精確性和穩(wěn)定性，同時通過高斯過程回歸實現(xiàn)了對未知形狀目標(biāo)擴展外形的準(zhǔn)確估計。

1 高斯過程下的星凸型擴展目標(biāo)建模

1.1 高斯過程回歸

目前，高斯過程廣泛應(yīng)用于機器學(xué)習(xí)、統(tǒng)計學(xué)和通信處理中來實現(xiàn)對信號的分類與識別[8-9]。簡單來說，高斯過程可以看作是一個分布函數(shù)f(u)，并通過均值函數(shù)μ(u)和協(xié)方差函數(shù)k(u,u′)來定義：

f(u)=GP(μ(u),k(u,u′))

其中：

μ(u)=E[f(u)]

k(u,u′)=E[(f(u)-μ(u))(f(u′)-μ(u′))T]

高斯過程通過輸入的訓(xùn)練數(shù)據(jù)來學(xué)習(xí)未知函數(shù)，現(xiàn)給出以下量測模型：

zk=f(uk)+ek

其學(xué)習(xí)過程主要表現(xiàn)為:給定一組量測z=[z1,...,zN]T以及他們對應(yīng)的輸入u=[u1,...,uN]T，通過高斯過程來學(xué)習(xí)函數(shù)f，使得當(dāng)輸入為uf=[u1，f,...,uNf， f]T時，可以根據(jù)學(xué)習(xí)的函數(shù)估計出對應(yīng)的函數(shù)值f=[f(u1，f),...,f(uNf， f)]T。根據(jù)文獻[7]中推導(dǎo)，可知量測值zk和函數(shù)值f服從聯(lián)合高斯分布:

由以上聯(lián)合高斯分布，可以很容易得到似然函數(shù)和初始先驗概率：

p(zk|f)=N(zk;Hk，ff,Rk, f)

(1)

p(f)=N(0;P0, f)

其中：

Hf(uk)=K(uk,uf)[K(uf,uf)]-1

Rf(uk)=k(uk,uk)+R-

K(uk,uf)[K(uf,uf)]-1K(uf,uk)

P0, f=K(uf,uf)

通過式(1)獲得的似然函數(shù)，建立狀態(tài)空間模型，運用卡爾曼濾波器實現(xiàn)高斯過程回歸。

fk+1=Fffk+Qf,wk, f～N(0,Qf)

(2a)

zk=Hf(uk)fk+ek, f,ek,f～N(0,Rf(uk))

(2b)

f0～N(0,P0, f)

(2c)

其中：

Ff=e-αTI

(3)

Qf=(1-e-2αT)K(uf,uf)

(4)

1.2 高斯過程回歸下的星凸形擴展目標(biāo)建模

目前，通過星凸模型對擴展目標(biāo)進行建模，并結(jié)合高斯過程回歸的學(xué)習(xí)特性，實現(xiàn)對擴展目標(biāo)外形的估計。由星凸模型的定義可知，目標(biāo)的外形可以通過半徑函數(shù)r=f(θ)來表示。當(dāng)傳感器獲得的量測來源于目標(biāo)表面時，將量測方程建模為:

zk,l=ck+sk,lp(θk,l)f(θk,l)+ek,l

(5)

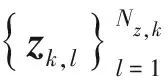
f(θ)=GP(μ(θ),k(θ,θ′))

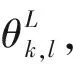
(6)

將式(2)、式(6)代入式(5)中，可以得標(biāo)準(zhǔn)的量測方程，其表達式為：

(7)

其中：

2 高斯過程下的星凸型擴展目標(biāo)高斯粒子濾波算法

高斯粒子濾波器參見文獻[10-11],此處不再贅述。現(xiàn)根據(jù)1.2節(jié)推導(dǎo)，將擴展目標(biāo)建模為:

xk+1=Fxk+wk,wk～N(0,Q)

zk=hk(xk)+ek,ek～N(0,Rk)

x0～N(μ0,P0)

其中：

Rk=diag[Rk,1,…,Rk,n]

hk(xk)=[hk,1(xk)T,…,hk,n(xk)T]T

F=diag(Fn,Ff)

Q=diag(Qn,Qf)

Ff、Qf由2.1節(jié)中式(3)、式(4)確定，F(xiàn)n、Qn與目標(biāo)的運動有關(guān)，具體參數(shù)在仿真實驗中給出。

高斯過程下的星凸型擴展目標(biāo)高斯粒子濾波算法主要思想為：通過高斯粒子濾波采樣獲得目標(biāo)的運動位置ck、運動方向ψk及運動速度c′，并根據(jù)推導(dǎo)的式(7)，采用卡爾曼濾波器實現(xiàn)高斯過程回歸，完成對目標(biāo)擴展外形fk的估計。所關(guān)注的聯(lián)合后驗概率密度為:

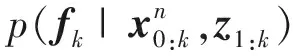
所提算法偽代碼如下所示:

初始化:for all Particles,i=1,...,N do f sample xn,(i)0 set initial weights w(i)0=1N set initial GP statistics f(i)0 end for 迭代:for k=1,...,N do for all particles, i=1,...,N do sample from xn,(i)k using π(xk|z1:k)=N(xk|k-1,Pk|k-1) update f(i)k using a Kalman filter (2) update the weights w～(i)k using w^ik=p(zk|x～ik)(x～ik|z1:k-1)π(x～ik|z1:k)=p(zk|x～ik)N(xk|k-1,Pk|k-1)π(x～ik|z1:k) normalize the weights using wik=w^ik∑Ni=1w^ik end for end for

3 仿真實驗與分析

將所提算法與文獻[7]中的GP EKF算法和文獻[12]中標(biāo)準(zhǔn)的RM算法進行比較分析，對所提算法對擴展目標(biāo)外形估計和跟蹤穩(wěn)定性兩方面性能進行驗證。在外形估計方面，文中選擇交集并集比[13-14](intersection over union, IOU)進行評估；在跟蹤精度及穩(wěn)定性方面，選擇常用的均方根誤差(root-mean-square error, RMSE)進行評估。

3.1 實驗參數(shù)設(shè)置

在這里考慮兩種目標(biāo)的外形：星凸型和橢圓形。實驗一假設(shè)星凸型目標(biāo)的長半軸為0.9 m，短半軸為0.3 m；實驗二假設(shè)橢圓形目標(biāo)長軸為2 m，短軸為1 m。兩個實驗除擴展目標(biāo)外形不同，其余設(shè)定均相同。

仿真中假設(shè)擴展目標(biāo)的運動軌跡為直線和轉(zhuǎn)彎的組合。目標(biāo)首先以2 m/s的速度作直線運動，然后轉(zhuǎn)彎，轉(zhuǎn)彎同時伴隨著目標(biāo)自身的旋轉(zhuǎn)，轉(zhuǎn)彎后繼續(xù)作直線運動。量測在目標(biāo)表面產(chǎn)生，服從泊松分布，泊松率為10，尺度變換因子sk,l～N(0.67,0.05)，雜波泊松率為10。目標(biāo)位置和旋轉(zhuǎn)方向建模為勻速模型為

3.2 仿真結(jié)果與分析

實驗一

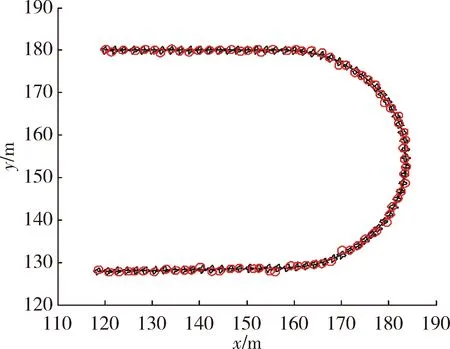
圖1 RM模型濾波結(jié)果

在實驗一中，當(dāng)擴展目標(biāo)外形為星凸型時，RM算法、GP EKF算法及文中所提算法的濾波結(jié)果分別為圖1、圖3、圖5 所示，圖2、圖4、圖6為其對應(yīng)的局部放大圖。在外形估計方面，從圖中可以較為直觀地看出GP EKF算法及文中所提算法對目標(biāo)外形估計較為準(zhǔn)確，而RM算法只能給出目標(biāo)外形的橢圓近似；在跟蹤精度方面，GP EKF算法在目標(biāo)不確定性大的情況下，跟蹤精度及穩(wěn)定性較差，其主要原因在于EKF模型對預(yù)測產(chǎn)生的誤差很敏感。相比之下， RM算法及文中所提算法的跟蹤精度較好且更穩(wěn)定。表1給出了3種濾波算法的平均交集并集比及均方根誤差兩個定量評價指標(biāo)。從表1更直觀準(zhǔn)確的看出文中所提算法在目標(biāo)外形估計及跟蹤精度、穩(wěn)定性方面，均優(yōu)于RM算法及GP EKF算法。

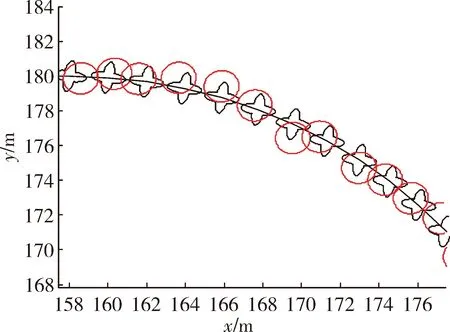
圖2 RM濾波局部放大圖

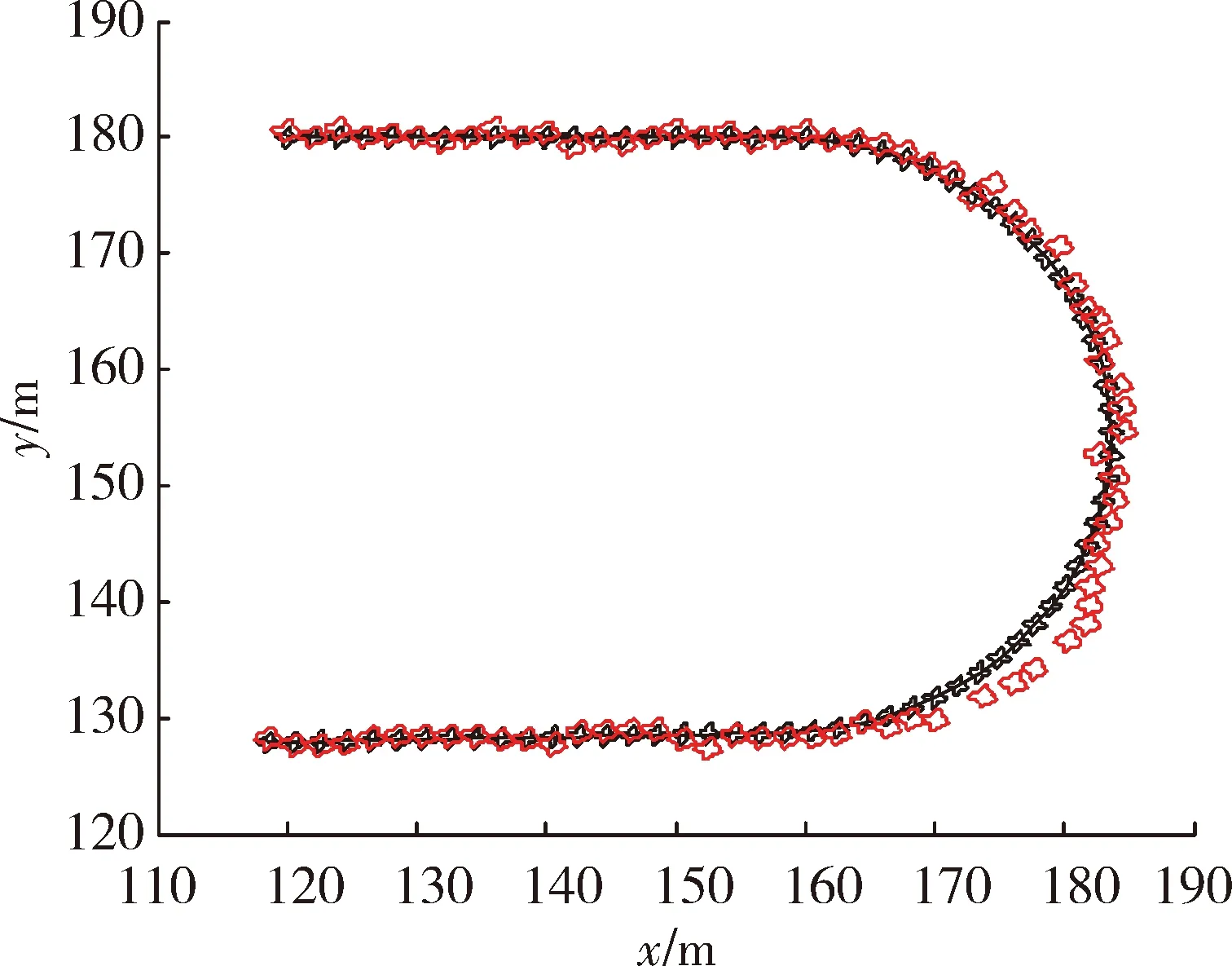
圖3 GM EKF算法濾波結(jié)果

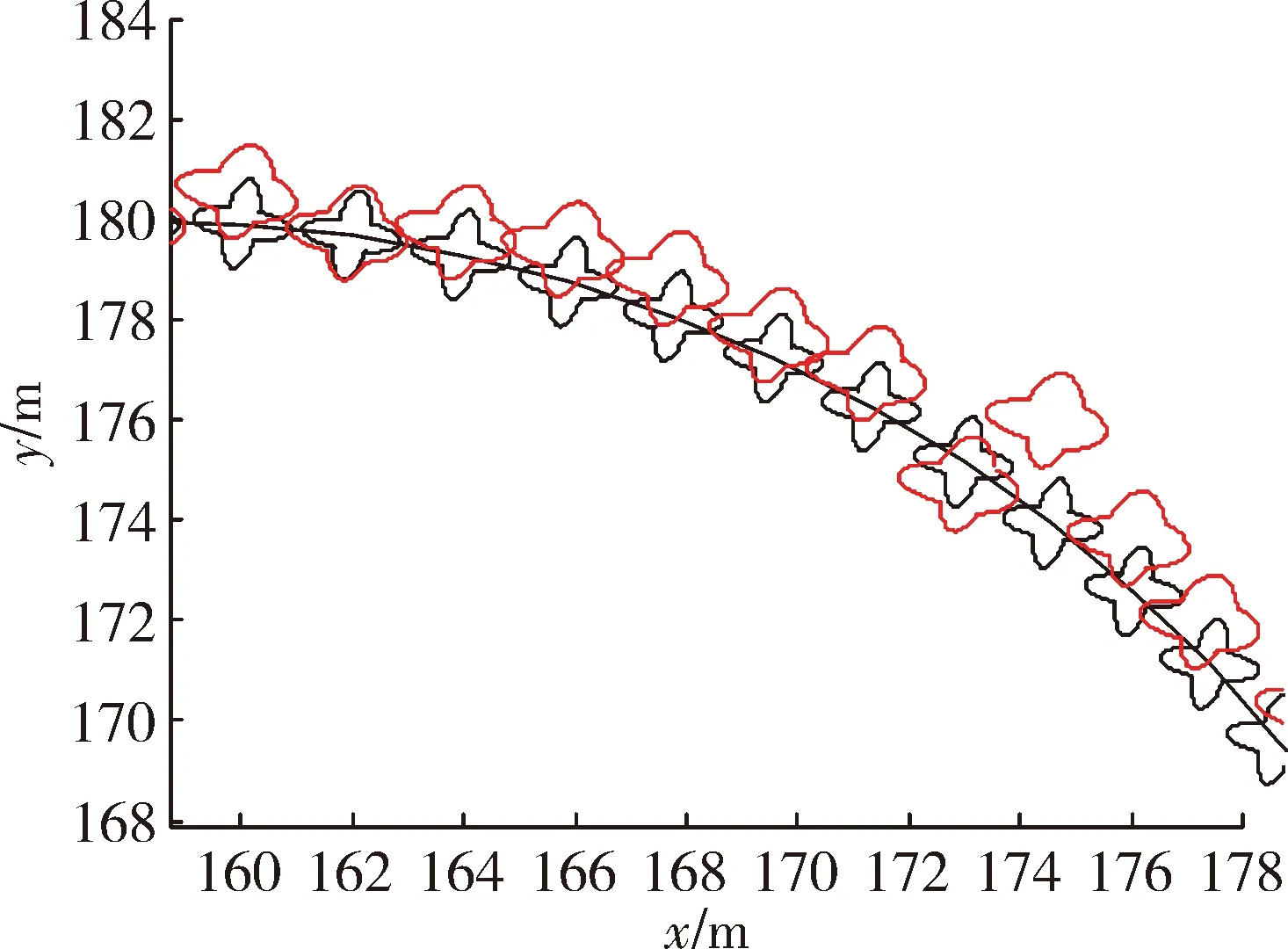
圖4 GM EKF濾波局部放大圖

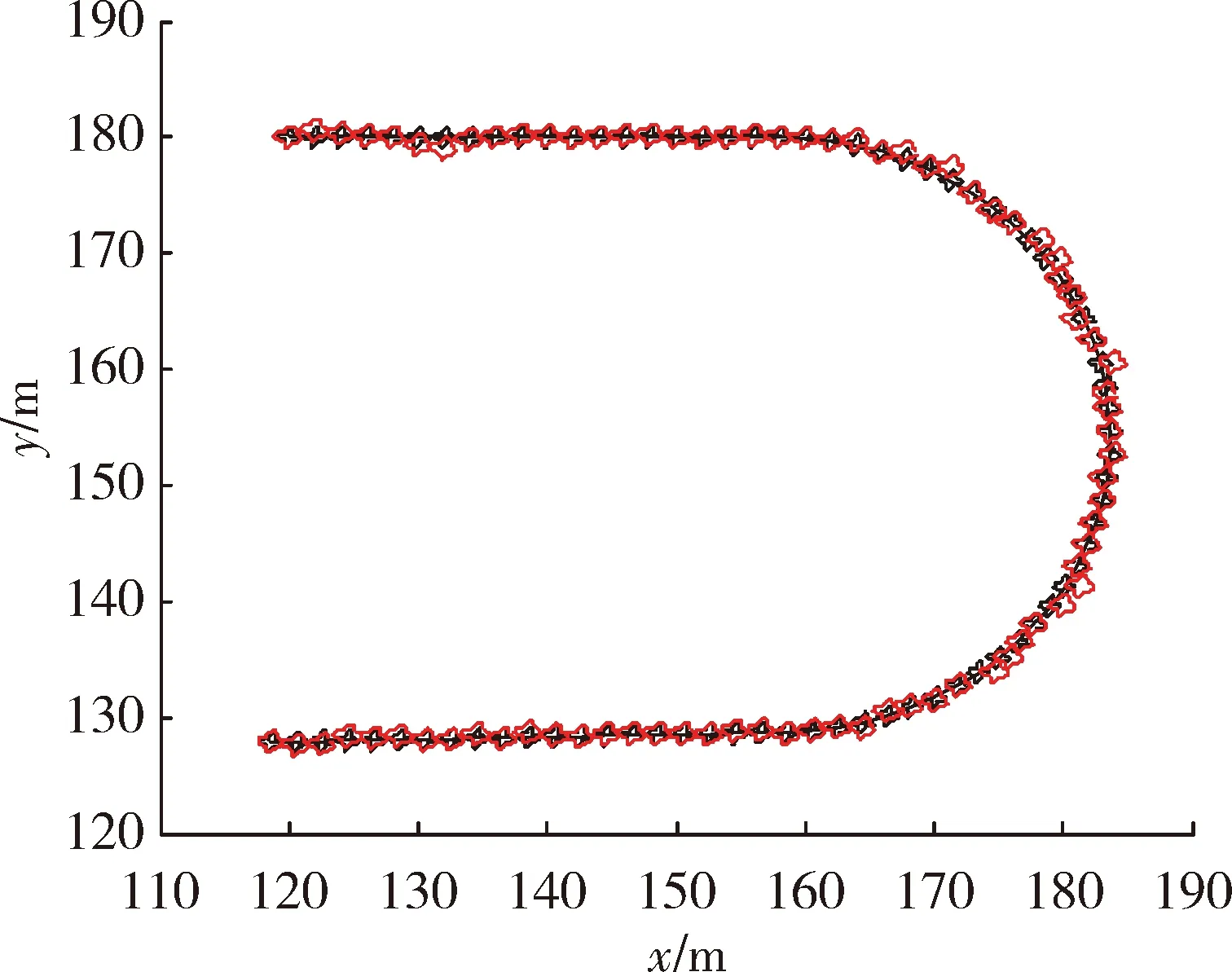
圖5 文中所提算法濾波結(jié)果

圖6 文中所提算法濾波局部放大圖

表 1RMSE與IOU對比

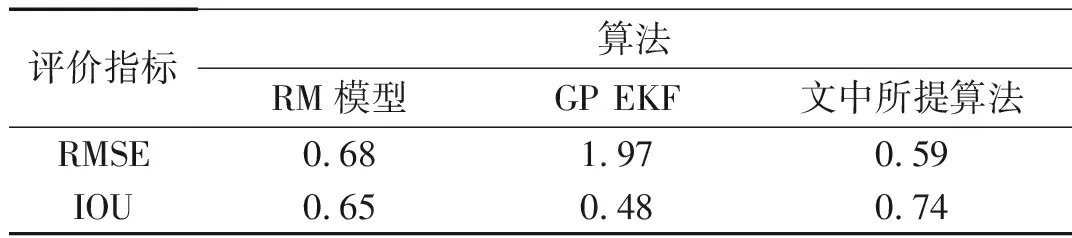
評價指標(biāo)算法RM模型GP EKF文中所提算法RMSE0.681.970.59IOU0.650.480.74

實驗二

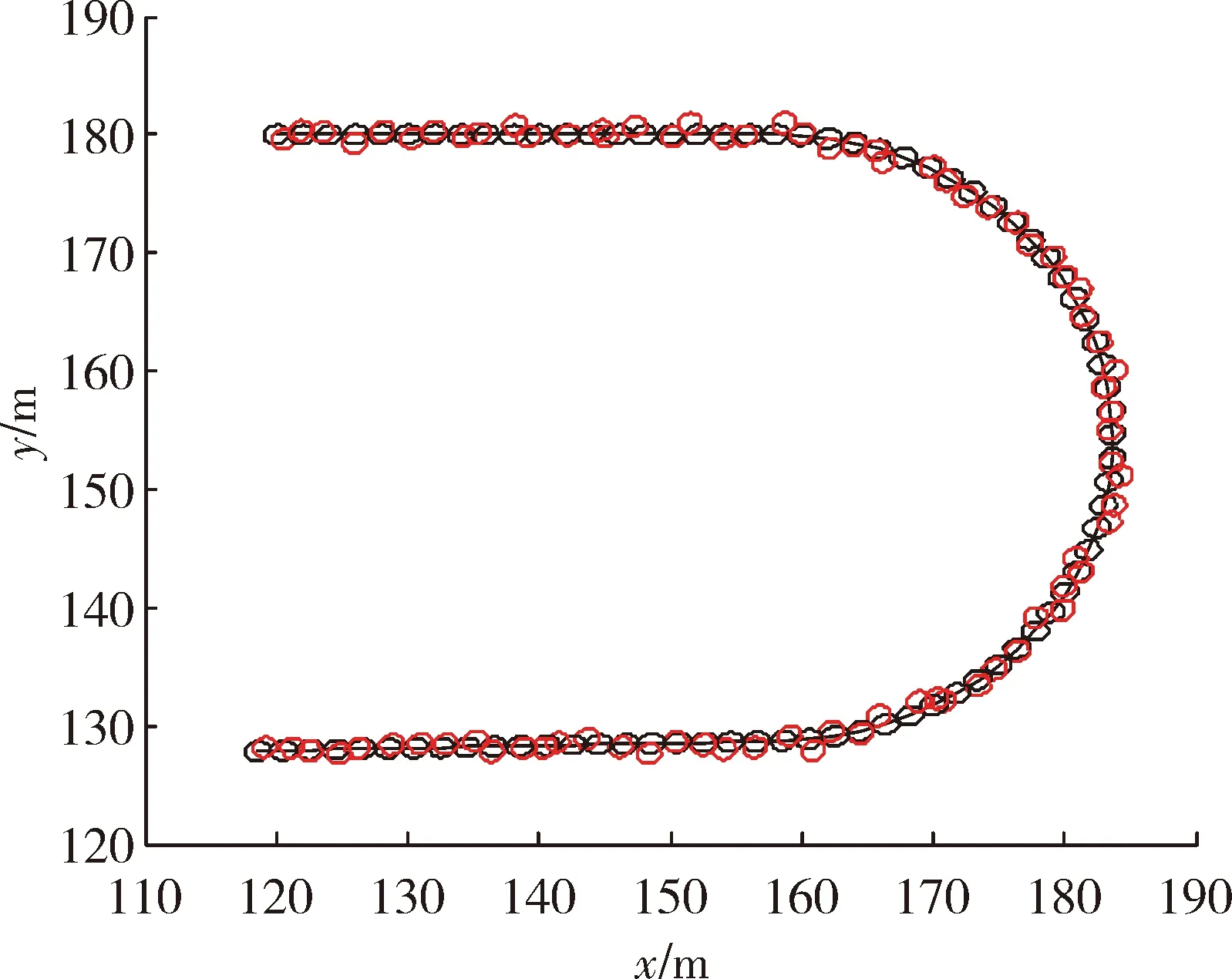
圖7 RM模型濾波結(jié)果

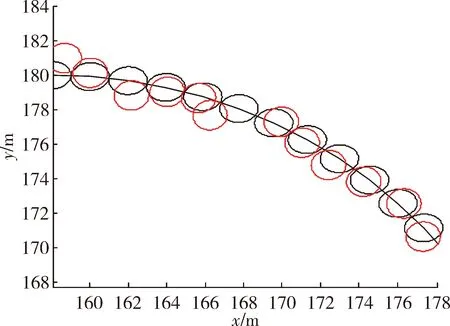
圖8 RM濾波局部放大圖

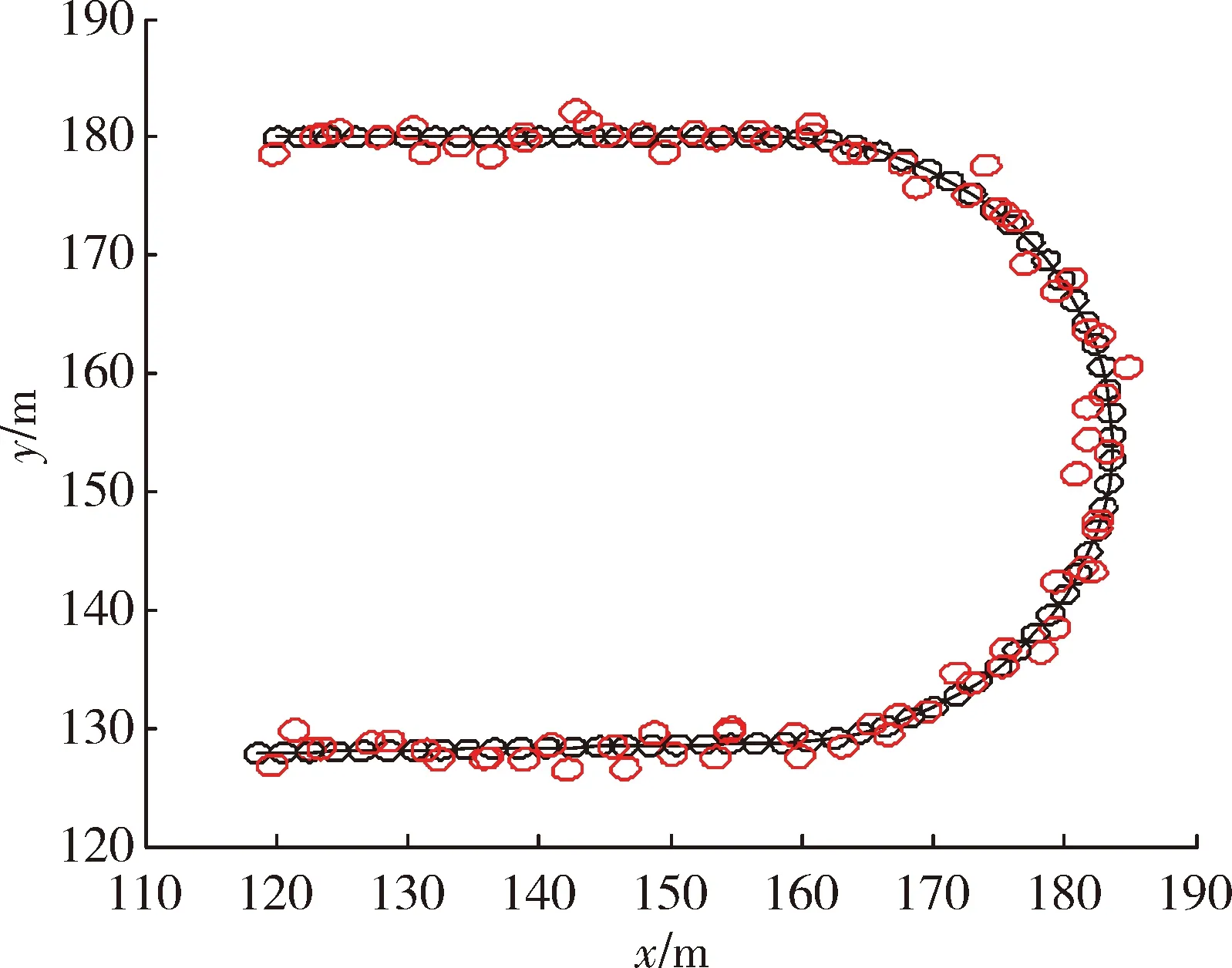
圖9 GM EKF算法濾波結(jié)果

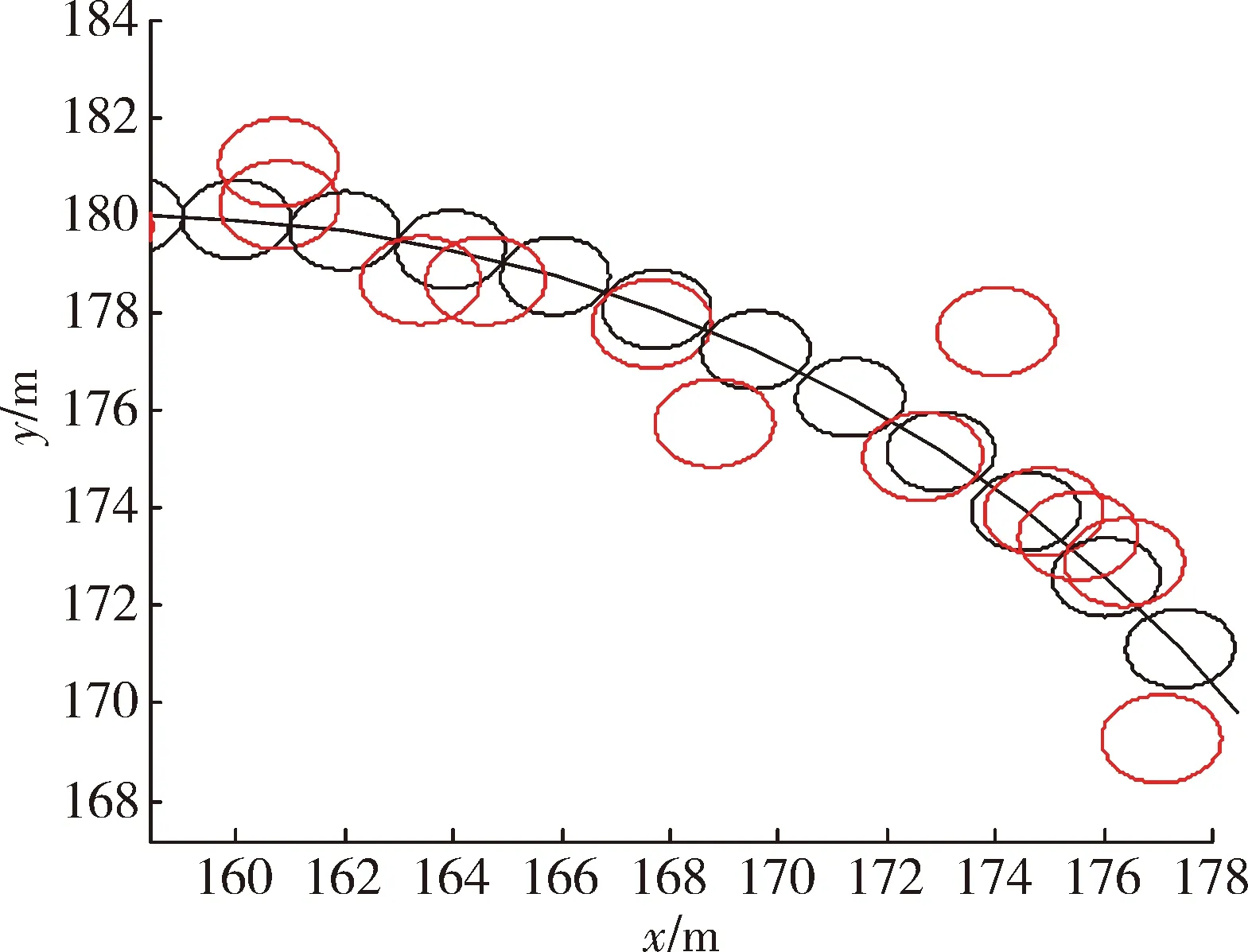
圖10 GM EKF濾波局部放大圖

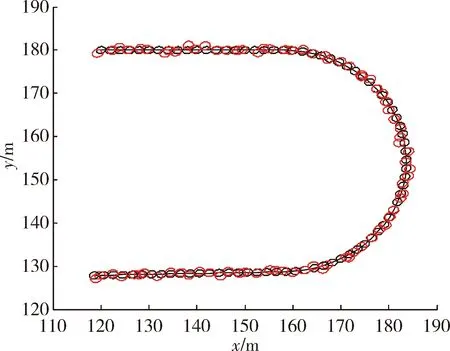
圖11 文中所提算法濾波結(jié)果

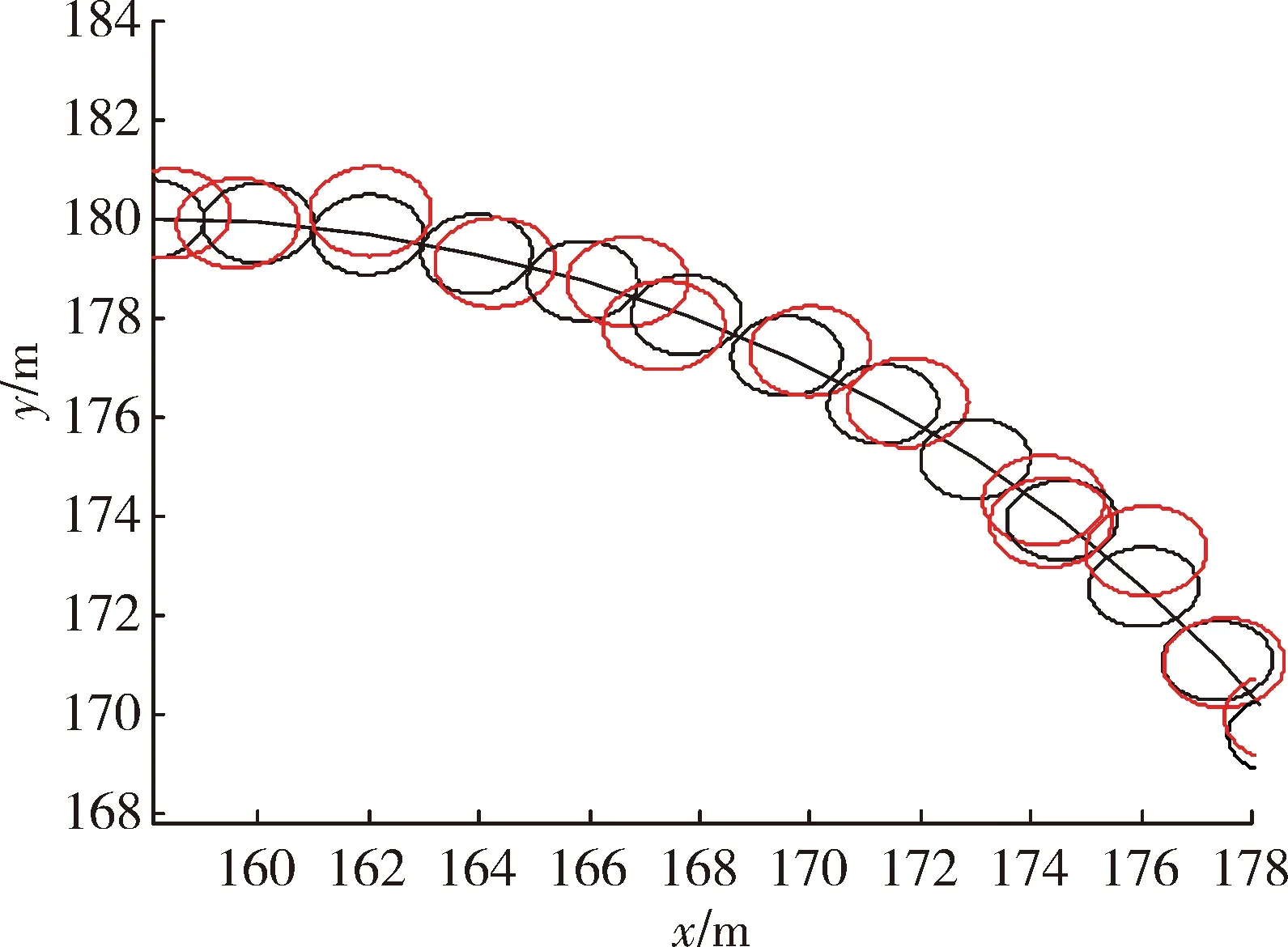
圖12 文中所提算法濾波局部放大圖

在實驗二中，當(dāng)擴展目標(biāo)外形為橢圓形時，RM算法、GP EKF算法及文中所提算法的濾波結(jié)果分別為圖7、圖9、圖11 所示，圖8、圖10、圖12為其對應(yīng)的局部放大圖。表2給出了三種濾波算法的平均交集并集比及均方根誤差兩個定量評價指標(biāo)。與實驗一中結(jié)果類似，在跟蹤橢圓形目標(biāo)時，文中所提算法也能很好地給出其擴展形態(tài)，且具有較好的跟蹤精度及穩(wěn)定性。

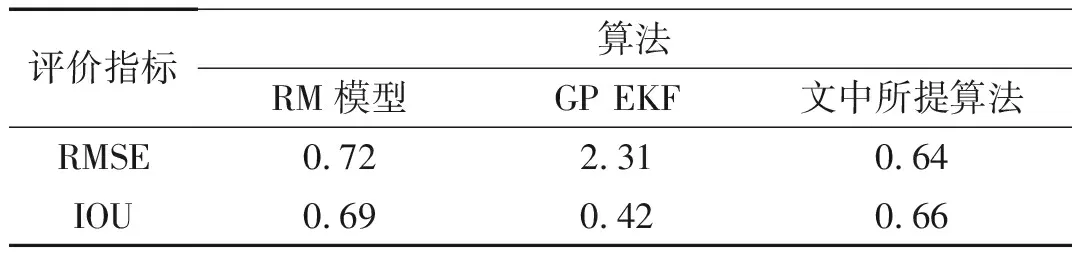
表 2 RMSE與IOU對比

4 結(jié)束語

文中提出一種高斯過程回歸下的擴展目標(biāo)高斯粒子濾波算法，該算法通過機器學(xué)習(xí)中的高斯過程可以很好地學(xué)習(xí)擴展目標(biāo)外形，避免了現(xiàn)有算法中由于參數(shù)過多導(dǎo)致計算復(fù)雜的問題，同時基于高斯粒子濾波魯棒性強，較好解決粒子退化的特性，對擴展目標(biāo)進行跟蹤。文中所提算法是一個通用模型，可以應(yīng)用于其他隨機超曲面模型[15-16]中，下一步將對算法向多個擴展目標(biāo)進行推廣,同時為了減少計算量，在考慮角度非線性變化并不大情況下，可以將旋轉(zhuǎn)角度改用EKF進行更新。