戰術級捷聯慣導方位裝訂的半自主對準*

崔 瀟，秦永元，楊小康，梅春波

(1 西北工業大學自動化學院， 西安 710129； 2 西安現代控制技術研究所, 西安 710065)

0 引言

常規火箭彈采用捷聯慣導進行制導改造后，可顯著增加有效射程、打擊精度大幅提高，制導火箭彈在世界各國得到了廣泛的應用，成為火箭彈發展的主要趨勢[1-2]。

由于戰術條件和彈載捷聯慣導自身器件精度的限制，火箭彈無法單純依靠自身完成初始對準，一種方案可采用依靠發射車裝備的高精度慣導進行傳遞對準[3]，但是需要發射架進行俯仰、回轉機動，對準精度也受到時空同步等因素影響；另一種方案采用方位裝訂，以速度+方位為量測的卡爾曼濾波對準方案[4]。兩種對準方案均涉及濾波器設計，存在收斂時間長以及受初始條件參數影響等影響。因此，研究基于方位裝訂的捷聯慣導快速初始對準具有較大工程應用價值。

1 坐標系定義

為便于分析，定義如下坐標系：

1)彈體坐標系b：原點位于彈體質心，xb、yb、zb分別為沿彈體的前、上、右，xbybzb構成右手直角坐標系；

2)當地水平坐標系H：原點位于彈體所在點，xH為xb在當地水平面內的投影，zH沿當地地垂線，向上為正，yH與xH、zH構成右手坐標系。

3)當地地理坐標系g：原點位于載體所在點，yg軸沿地理垂線指向上，xg、zg軸在當地水平面內且xg沿當地經線方向指向北，zg沿當地緯線切線方向指向東，即“北天東”地理坐標系。

2 水平自對準

2.1 水平姿態矩陣

設對準時刻導彈的航向角為ψ(北偏東為正)，俯仰角為θ，橫滾角為γ，則:

(1)

(2)

圖1 地理坐標系與載體坐標系轉換關系圖

(3)

2.2 T2周期內的水平姿態四元數計算

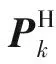
tk=kT2=kNT1

(4)

上述時間周期關系如圖2所示。

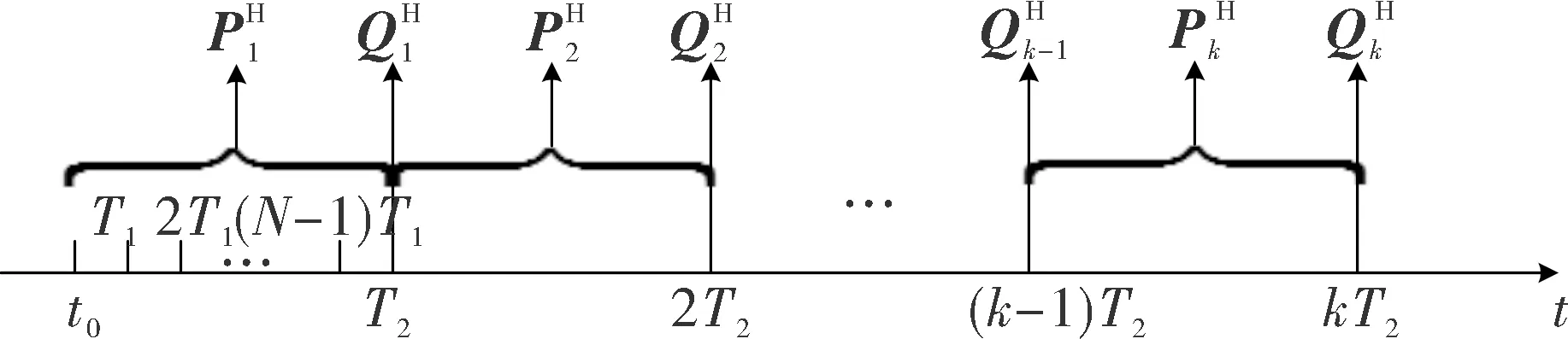
圖2 T1周期、T2周期、水平姿態四元數間的關系

忽略彈體晃動，則加速度計輸出為：

(5)

即

(6)

假設加速度計輸出經過I-F變換。記在第k個T2周期內，第n個T1周期內的加速度計輸出積分為δVxk(n)，δVyk(n)，δVzk(n)，即有：

(7)

則在第k個T2周期內加速度計輸出的積分為：

ΔVxk=NT1gsinθ=T2gsinθ

(8a)

ΔVyk=NT1gcosγcosθ=T2gcosγcosθ

(8b)

ΔVzk=-NT1gsinγcosθ=-T2gsinγcosθ

(8c)

記

(9)

由于加速度計存在測量誤差，彈體存在晃動干擾，所以gk≈g·T2。

記

(10)

則由式(10)得：

(11a)

(11b)

(11c)

(11d)

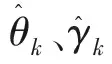
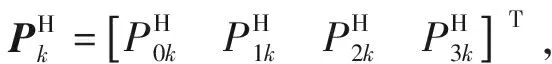
(12)

(13)

(14)

(15)

(16)

(17)

(18)

(19)

(20)

(21)

(22)

(23)

(24)

(25)

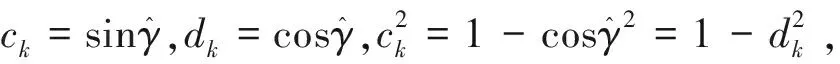
(26)

由式(19)、式(21)、式(23)得：

(27)

2.3 tk時刻的水平姿態四元數計算

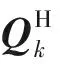
(28)

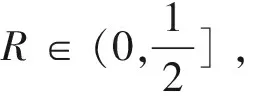
2.4 引入外基準航向后的姿態四元數

設tk=kT2=kNT1時刻水平對準結束，外基準引入的航向角為ψ，則與ψ對應的四元數為：

(29)

由于

(30)

根據姿態陣的矩陣乘與四元數乘之間的關系，得與式(29)對應的姿態四元數為：

(31)

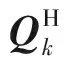
3 陀螺漂移估計

考慮如下四元數更新離散方程：

(32)

由文獻[5]已知：

(33)

則

(34)

式中:Δθx、Δθy、Δθz為在[tk,tk+1]時間間隔內的角增量。

假設陀螺輸出為：

(35)

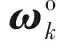
記

(36)

則誤差轉移矩陣ΔΦk可以表示為一個矩陣冪級數，冪級數第n項為Ο(‖δωkΔt‖n) ，如果只考慮一階近似，則:

ΔΦk≈M(δωk)Δt

(37)

式中:

(38)

將式(36)、式(37)代入式(32)，可得:

Qk+1=ΦkQk-ΔtM(δωk)Qk

(39)

定義矩陣:

(40)

則容易得:

M(δωk)Qk=Ξ(Q)δωk

(41)

則式(39)可寫為:

(42)

式中：wk為四元數更新誤差，是陀螺測量誤差的函數。

對于戰術級慣導，陀螺啟動常值漂移很大，若僅僅考慮陀螺儀的常值漂移δωk≈εb，則可得：

(43)

4 仿真分析

為進一步檢驗文中所提的半自對準方法的性能，進行了搖擺基座下對準的仿真。

4.1 仿真條件

1)彈體繞俯仰軸、橫滾軸和方位軸的搖擺運動，可看作由一系列幅值和頻率相近的正弦波來描述：

(44)

式中：θ、γ、φ分別為繞俯仰軸、橫滾軸和方位軸的搖擺角度；θm、γm、φm分別為搖擺角度幅值；ωθ、ωγ、ωφ為搖擺的角頻率；θ0、γ0、φ0為搖擺的初始相位。

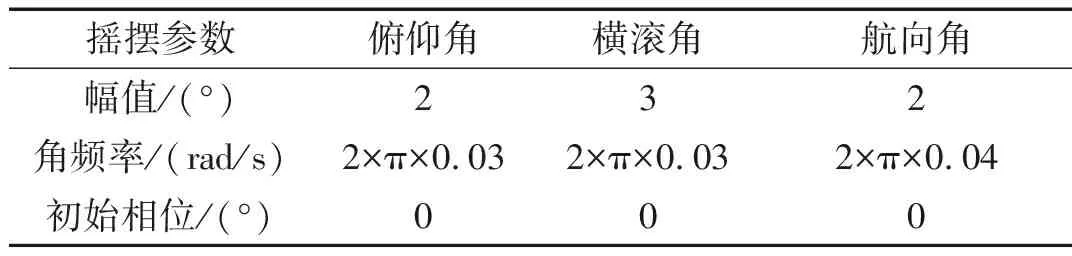
表1 搖擺參數設置

2)慣導參數設置：

表2 慣導參數設置

3)慣導采樣周期：0.01 s(即T1)；T2=0.1 s。

4.2 仿真結果

根據4.1設置的仿真條件，仿真結果如圖3～圖5所示。

圖4 搖擺基座對準估計結果(不同陀螺常值漂移)

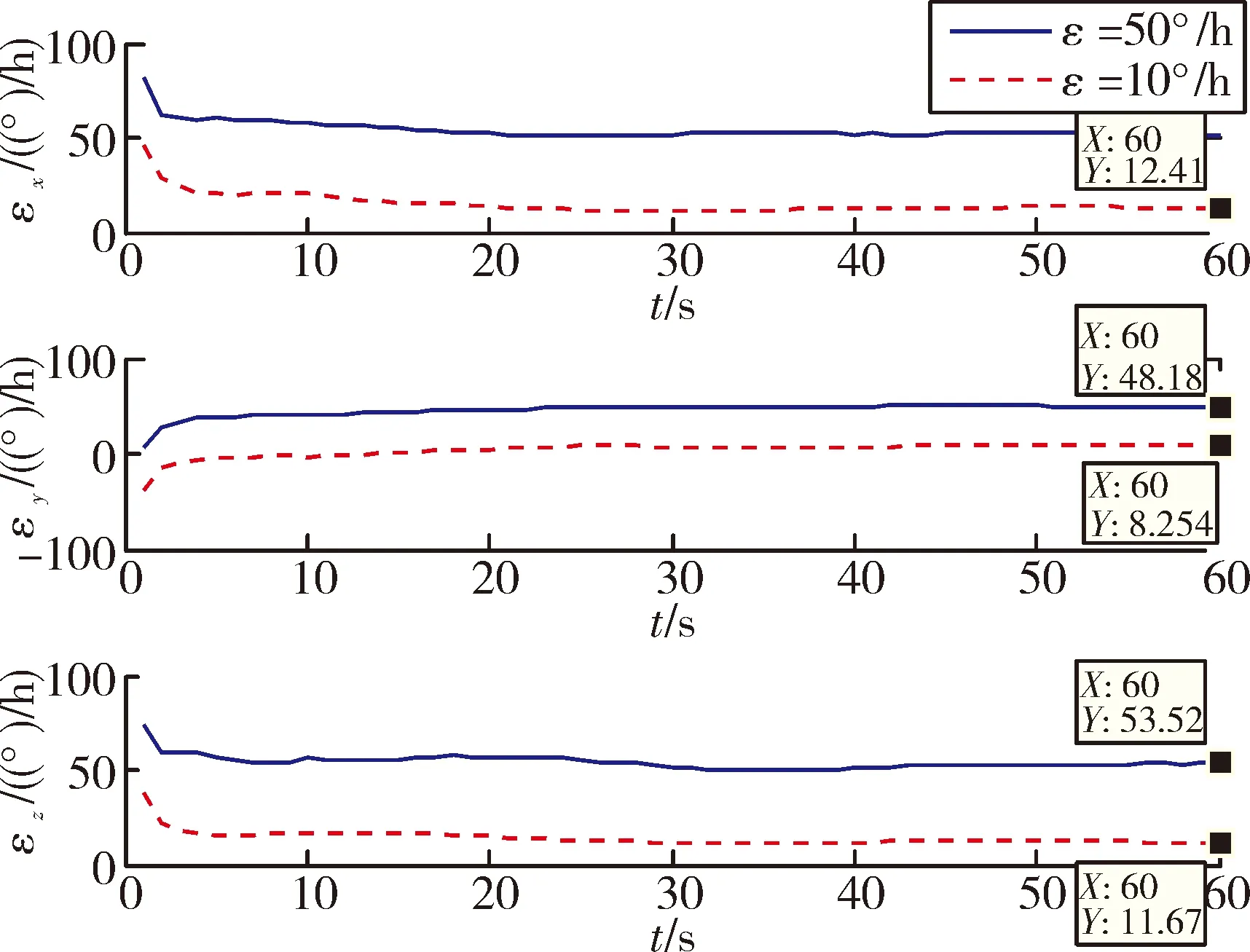
圖5 陀螺漂移估計結果(T2=0.1 s)

圖3中實線表示真實姿態曲線，虛線表示對準結果，從圖3中可以看出，由于航向角由外部裝訂，基本無誤差，水平自對準姿態可以跟蹤真實姿態，只是存在時間延遲，對比不同T2的結果，T2周期越大，造成的延遲也越大，所以，實際工程中，根據加速度噪聲大小、彈體晃動幅度及頻率等因素，適當調整T2周期。

為了驗證不同陀螺常值漂移對算法的影響，圖4給出了不同陀螺漂移下的對準結果，從圖4中可知，陀螺常值漂移不影響水平對準結果，結果和前面的分析一致。圖5給出了在同一更新周期T2下對陀螺漂移的估計結果，可知算法可以對陀螺常值漂移進行粗略估計，估計精度且與漂移大小無關。

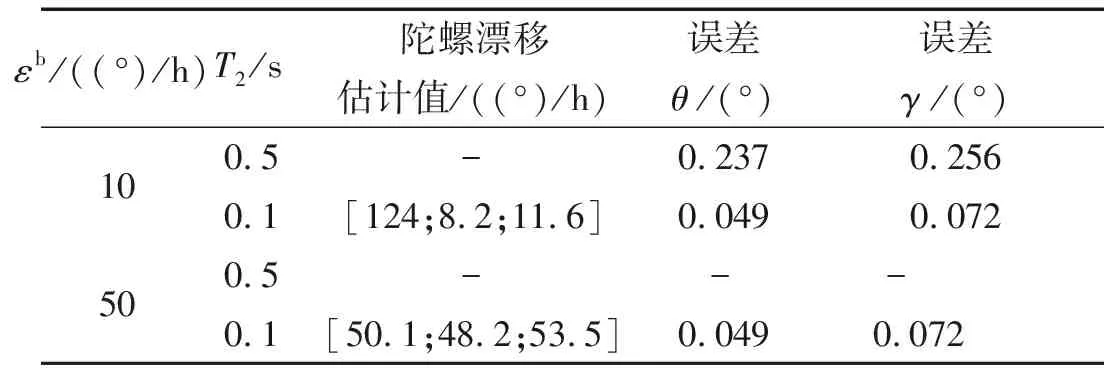
表3 對準結果統計

表3總結了對準結束時刻的對準精度。從表3中可知，減小更新周期T2對準精度也隨之提高，當T2=0.1 s時，對準精度在0.1°以內，而陀螺常值漂移大小不影響姿態對準結果。

5 結論

仿真結果表明：文中給出的戰術級捷聯慣導方位裝訂的半自主對準方法在對準的同時，還可對陀螺常值漂移進行粗略估計，但加速度計零偏無法得到估計。與傳統基于卡爾曼濾波對準方法相比，文中的方法具有運算簡單、計算量小和便于工程應用的優點，為火箭彈的對準提供了參考。