點火增長反應速率方程在LS-DYNA軟件中嵌入及應用
苗飛超,周霖,張向榮,曹同堂
(1.北京理工大學 爆炸科學與技術國家重點實驗室, 北京 100081; 2.安徽東風機電科技股份有限公司, 安徽 合肥 230000)
0 引言
沖擊起爆特性是炸藥的重要性能之一,是作用可靠性和使用安全性評價的重要依據。Lee & Tarver點火增長反應速率方程[1-2]已廣泛用于沖擊起爆的數值模擬,并成功重現了圓筒實驗[3]、拉氏分析實驗[4-6]、飛片沖擊實驗[7]、微通道裝藥爆轟實驗[8]的實驗結果。但點火增長反應速率方程的參數較多(三項式的參數多達15個)且參數間存在關聯[9],這導致點火增長反應速率方程的標定存在較大的困難。為此,Murphy[9]對反應速率方程的形式進行了修改,得到了參數更少,參數間無關聯的反應速率方程。由于改進的反應速率方程保留了Lee & Tarver模型中點火增長的概念,因此兩者在模擬沖擊起爆方面具有相同的功能。盡管改進的反應速率方程具有以上優點,但目前為止,大型商業軟件,包括LS-DYNA、AUTODYN和Abaqus等中并未包含該反應速率方程。
因此,本文將改進的點火增長模型以自定義狀態方程的形式嵌入LS-DYNA軟件中,并采用此模型對DNAN基熔注炸藥的沖擊起爆過程進行了數值模擬,通過對比計算壓力曲線和實驗壓力曲線標定了改進的模型參數。
1 改進的點火增長反應速率方程
1.1 模型簡介
三項式的Lee & Tarver反應速率方程[2]的表達式為
(1)
式中:F為反應分數;p為壓力;ρ和ρ0分別是當前時刻和初始時刻的密度;I、b、a、x、G1、c、d、y、G2、e、g、z、Figmax、FG1max和FG2min為15個可調參數;等號右側3項分別為點火項、慢速增長項和快速完成項。Murphy[9]保留Lee & Tarver反應速率方程中點火增長的概念,對上述反應速率方程進行了改進。改進的反應速率方程表達式為

(2)
式中:η=ρ/ρ0-1;Freq、figmax、Ccrit、Eeta1、Grow1、Es1、em、Grow2、Es2、en為10個可調參數。與Lee & Tarver反應速率方程相比,改進的點火- 增長反應速率方程具有以下優點:
1)慢速增長項和快速完成項的系數相關性弱。改進的點火增長反應速率方程用sin(πFEs)代替了Lee & Tarver反應速率方程慢速增長項和快速完成項的(1-F)mFn(m為c或e,n為d或g)。顯然,Es只影響sin(πFEs)曲線的形狀,峰值大小始終為1.0,而m和n的大小同時影響(1-F)mFn曲線的峰值和形狀。換言之,調整曲線的形狀時,Lee & Tarver模型需要同時改變2個參數(m和n),而改進的模型只改變1個參數(Es),簡化了參數的標定過程。
2) 反應速率方程的參數較少。改進的反應速率方程的參數有10個,比Lee & Tarver反應速率方程少5個,進一步降低了參數標定的難度。
1.2 模型嵌入LS-DYNA軟件
鑒于改進的點火- 增長反應速率方程具有上述優點,本文將改進的點火- 增長反應速率方程以自定義狀態方程的形式嵌入LS-DYNA軟件中。下面對自定義狀態方程計算中,未反應炸藥和爆轟產物的混合法則、狀態方程形式和各物理量的求解過程進行介紹。其中狀態方程混合采用Cochran等[10]的算法。
部分反應炸藥是未反應炸藥和爆轟氣體產物的混合物,假設兩種組分處于壓力p和溫度T平衡狀態,即
(3)
式中:下標m代表部分反應炸藥;下標s代表未反應炸藥;下標g代表爆轟氣體產物。部分反應炸藥的相對體積Vm和內能Em,滿足加和特性,
(4)
式中:相對體積V=v/v0,v和v0分別是當前時刻和初始時刻的比容;內能E=e/e0,e和e0分別是當前時刻和初始時刻的比內能。
未反應炸藥和爆轟產物均采用含溫度的JWL狀態方程[2],其形式為
(5)
式中:*為s或g,分別代表未反應炸藥和爆轟產物;A、B、R1、R2、ω、CV均為可調參數。
溫度、壓力和反應分數等物理量的求解過程如下:
1)溫度的計算。
為簡化計算,將能量方程轉化為溫度方程。溫度方程的表達式為
(6)
式中:Sij為偏應力張量;εij為應變張量;q為人工黏性項;CVm、J以及H分別為
(7)
采用預測- 校正格式對(6)式進行顯示差分計算,可得到ΔTm.
2)真實體積分數和壓力的計算。
定義β=(1-F)Vs/Vm為未反應炸藥的真實體積分數[10],則Vs和Vg可表示為
Vs=βVm/(1-F),
(8)
Vg=(1-β)Vm/F.
(9)
由于未反應炸藥和爆轟氣體產物處于壓力平衡,因此
pg-ps=δ(Tm,Vm,F,β)=0.
(10)
在給定Tm、Vm、F的條件下,采用牛頓迭代法對(10)式進行迭代求解,迭代變量為β. 在迭代過程中,通過(8)式和(9)式計算Vs和Vg,并將Vs和Vg代入單組分狀態方程中計算ps和pg.β通過迭代收斂時,得到pm=0.5(ps+pg)。
3)反應分數F的計算。
反應速率方程可表示為

(11)
式中:R為任意函數。本文采用Cochran等[10]的差分格式計算該方程,該格式兼具顯示格式和隱式格式的優點,其形式為
(12)
式中:上標n代表第n個時間步;Δt為時間步長;
(13)
(13)式中λ的取值方法可保證反應速率方程的差分求解過程是完全穩定的。各物理量在一個時間步長內的迭代求解過程如圖1所示。

圖1 各物理量迭代求解流程圖Fig.1 Flow chart of iteration for updating the variables
2 沖擊起爆數值模擬
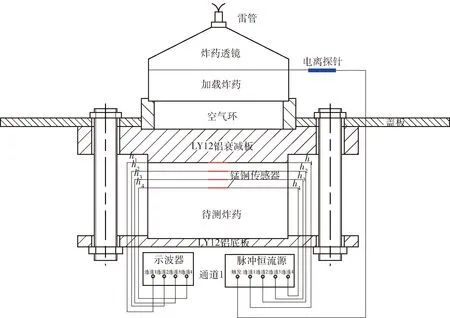
圖2 一維拉格朗日分析測試系統示意圖[5]Fig.2 Schematic diagram of one-dimensional Lagrange analysis and measurement system[5]
Cao等[11]采用如圖2所示的一維拉格朗日分析測試系統,測量了DNAN基熔注炸藥(DNAN 29.5%/RDX 40%/Al 30%/N-甲基-4-硝基苯胺(MNA)0.5%)沖擊起爆過程中的壓力曲線。測試時,由透鏡產生的平面波經空氣隙和鋁板衰減后入射到炸藥中。待測炸藥由3個厚度3 mm藥片和1個厚度20 mm的藥片組成,藥片直徑均為50 mm. 4個錳銅傳感器分別安裝在距離鋁衰減板0 mm(h1)、3 mm(h2)、6 mm(h3)和9 mm(h4)位置處。最終實驗得到圖2中4個傳感器記錄的壓力曲線。本文以該壓力曲線為基礎,標定改進的點火增長模型參數。通過對比計算壓力曲線和實驗壓力曲線,驗證改進的點火增長模型能否正確模擬DNAN基熔注炸藥的沖擊起爆過程。
2.1 幾何模型
為節省計算內存和計算時間,只建立了待測炸藥的幾何模型,并將實驗測得的圖2中衰減板與炸藥界面處(即圖2中h1)的壓力變化歷史作為炸藥的壓力邊界條件。圖3中4個觀測點位置對應圖2中4個錳銅傳感器位置,即h1(0 mm)、h2(3 mm)、h3(6 mm)和h4(9 mm),以便將計算值與實驗值對比。

圖3 數值模擬幾何模型Fig.3 Geometric model of numerical simulations
2.2 材料參數
未反應炸藥和爆轟產物狀態方程參數來自文獻[11]。但文獻[11]中未反應炸藥采用的是Gruneisen狀態方程。考慮到本文采用的是JWL狀態方程,因此需要將Gruneisen狀態方程擬合為JWL狀態方程。本文采用遺傳算法對其進行擬合,具體擬合方法見文獻[12]。擬合結果如圖4所示,擬合參數如表1所示。

圖4 JWL狀態方程參數擬合Fig.4 Fitting result of JWL equation of state
反應速率方程參數通過試錯法優化得到。通過不斷調整反應速率方程參數,減小計算值相對實驗值的偏差。最終,優化得到的反應速率方程參數如表2所示。
2.3 計算結果與分析
采用表1和表2中的參數對圖3的模型計算,得到的計算值和實驗值如圖5所示。從圖5中可以看出,沖擊波到達時間和壓力駝峰對應時間重合度較高,計算值與實驗值吻合較好。但是,h3和h4處計算的壓力峰值與實驗值相差較大。這可能是封裝傳感器的聚四氟乙烯與炸藥的阻抗不匹配導致的。因此,在對計算結果進行評價時,應該更多的關注沖擊波到達時間、壓力變化趨勢和駝峰出現位置與實驗值是否吻合。從圖5來看,改進的點火增長模型能夠較好地描述炸藥的沖擊起爆過程。

表1 JWL狀態方程參數
注:DCJ為爆速,pCJ為爆壓,E0為內能。

表2 改進的點火增長反應速率方程參數

圖5 4個觀測點處的壓力時程曲線實驗值與計算值對比Fig.5 Comparison of experimental and simulated values of pressures at four fixed points
相對于軟件自帶模型,自定義模型可以輸出更多的計算信息,有助于判斷模型嵌入LS-DYNA軟件時采用的壓力更新算法是否可行。壓力更新算法中迭代變量的選擇尤為重要。本文2.2節中,采用牛頓法對(10)式進行迭代求解時取β為迭代變量,并沒有取Vs或Vg作為迭代變量,具體原因結合本次數值模擬計算結果分析如下。
圖6為本文數值模擬計算得到的4個觀測點處未反應炸藥相對體積的變化曲線。圖6中h2位置處,初始時刻Vs為1,到計算結束時約為33,變化范圍較大。因此,如果以Vs作為迭代變量,則迭代次數較多,計算效率低。此外,在傳感器有效記錄時間內,如果入射到炸藥中的沖擊波持續時間較短,則稀疏波的作用時間會比較長,Vs可能達到103量級。此時,在對Vs進行迭代時,容易出現不收斂情況,并且由于計算機存在舍入誤差,在計算時甚至會出現0/0型的錯誤。

圖6 4個觀測點處未反應炸藥相對體積Fig.6 Relative volumes of unreacted explosives at four fixed points
圖7為本文數值模擬計算得到的4個觀測點處爆轟產物相對體積的變化曲線。由圖7可知,Vg的變化范圍較小,將其作為迭代變量似乎可行。但是,在波陣面處,Vg的變化極為劇烈,類似于跳躍間斷點。因此,若將Vg作為迭代變量,在波陣面處進行迭代時很難收斂。

圖7 4個觀測點處爆轟產物相對體積Fig.7 Relative volumes of detonation products at four fixed points
圖8為本文數值模擬計算得到的4個觀測點處迭代變量β的變化曲線。由圖8可知,在整個計算過程中β始終在0~1的范圍內變化,β變化范圍較小。此外,整個計算過程中β光滑過渡,有助于快速收斂。本文計算中,每個網格的迭代次數不超過3次,證明本文所采用迭代算法是高效、可行的。因此,采用β作為迭代變量有利于減少迭代次數,提高計算效率。

圖8 4個觀測點處迭代變量βFig.8 Iterative variables β at four fixed points

圖9 4個觀測點處的壓力與相對體積路徑Fig.9 p-V paths at four fixed points
此外,自定義模型可以輸出更多的流場信息,有助于進一步觀察反應區結構,并對實驗設計提供指導。為了更詳細地描述沖擊起爆過程,可以對圖9中4個觀測點在p-V圖上的路徑與雨貢紐曲線和等熵線的關系進行分析。以h1處觀測點為例,沖擊波入射到炸藥中,壓力從0 GPa升高到7.5 GPa,落在雨貢紐曲線;隨后,炸藥開始反應,反應分數逐漸增加,(V,p)點逐漸向等熵線靠近;當相對體積為1.0(圖10中“+”)時,對應的反應分數為0.64,隨后繼續膨脹。其他3條曲線的過程類似。值得注意的是,h4處觀測點反應分數達到1時,相對體積為0.95. 而Chapman-Jouguet點對應的相對體積為0.72,所以在h4處仍未建立穩定爆轟。因此,如果想在實驗中記錄到穩定爆轟的狀態,可以適當增加最后一個傳感器位置到邊界的距離。

圖10 4個觀測點處反應分數Fig.10 Reaction fractions at four fixed points
3 結論
本文通過自定義狀態方程的形式將改進的點火增長模型嵌入LS-DYNA軟件,對DNAN基含鋁熔注炸藥沖擊起爆進行了數值模擬,并與實驗值進行了對比。得出以下結論:
1)計算得到的4個傳感器位置處的沖擊波到達時間與實驗值相差不超過0.2 μs,改進的點火增長模型能夠很好地描述炸藥的沖擊起爆過程。
2)以β作為迭代變量的壓力更新算法計算效率高。本文計算中,每個網格的迭代次數不超過3次。
3)將Lagrange位置處的壓力與相對體積路徑線與未反應炸藥的雨貢紐曲線、爆轟產物的等熵線畫在一張圖上有助于理解炸藥在沖擊起爆過程中的狀態變化、判斷該Lagrange位置處的炸藥是否達到穩定爆轟和深化對沖擊起爆過程的認識。

