旋轉尾翼彈箭極限圓錐運動穩定判據

陳亮， 劉榮忠， 郭銳， 席滔滔， 李培林， 朱桂利， 楊永亮, 邢柏陽, 高科

(1.中國航天科技集團有限公司 第七研究院 第七設計部， 四川 成都 610100; 2.南京理工大學 機械工程學院, 江蘇 南京 210094)

0 引言

圓錐運動為彈箭基本的角運動形式之一，是指彈軸繞速度線做圓錐擺動的運動過程。在彈箭氣動參數和結構特征參數滿足一定條件的情況下，彈箭發射時的初始擾動以及飛行過程中的不確定因素(如陣風等)均可能導致彈箭形成極限圓錐運動。20世紀60年代中期，美國Nitehawk探空火箭在所進行的50余次飛行試驗中，出現近20次發散的圓錐運動[1]。西班牙140 mm火箭彈在進行的28次飛行實驗中，有9次出現了圓錐運動，導致其飛行速度在1.5 s內降低了60%[2]，這對提高彈箭射程是不利的。

對于以母彈作為掃描探測平臺的掠飛靈巧彈藥而言，角運動規律對其穩態掃描特性及命中概率有顯著影響。當僅受線性空氣動力作用時，掠飛靈巧彈藥僅需滿足線性穩定條件，即可使初始擾動引起的攻角運動幅值隨弧長增長而逐漸被衰減為0°[3-4]，從而保證其在彈道末端具有相對穩定的彈體姿態。而當受非線性空氣動力作用時，掠飛靈巧彈藥在彈道末端可能產生攻角幅值不為0°的極限圓錐運動[5-6]。此時，彈載敏感器在空間和地面形成的掃描線必然隨彈軸的錐進運動而出現振蕩變化，從而影響目標捕獲概率，這是靈巧彈藥研制過程中必須加以避免的。因此，研究彈箭在非線性氣動力和力矩作用下的角運動規律，確定極限圓錐運動形成條件，對彈箭運動穩定性和命中概率研究具有重要意義。

國內外學者圍繞彈箭圓錐運動穩定性問題已取得了豐富的研究成果。Levy等[7]和Clare等[8]基于風洞實驗和理論推導證明了馬格努斯力和力矩等面外力和力矩是彈箭形成極限圓錐運動的直接原因。李臣明等[9]考慮由章動和進動引起的赤道阻尼力矩系數的差異，基于奇點理論和振幅平面法研究了彈箭在非對稱赤道阻尼力矩作用下形成極限圓錐運動的條件，但未考慮非線性靜力矩和非線性馬格努斯力矩的影響。鐘揚威等[10]基于微分方程Hopf分岔理論，研究了當某一參數(如空氣密度)改變對極限圓錐運動特性的影響，但該方法難以獲得具有明確解析關系的理論模型。鄧超[11]基于擬線性法推導了彈箭在非線性靜力矩和非線性馬格努斯力矩作用下的振幅平面方程，并分析了馬格努斯力矩系數線性部分和非線性部分對極限圓錐運動的影響，由于擬線性法需要人為引入附加限制條件，因此限制了其使用范圍。此外，文獻[5-6]對彈箭非線性角運動特性以及彈箭極限圓錐運動特性的相關研究方法、研究成果進行了全面系統的介紹，其中文獻[6]中5.5節基于改進擬線性法推導了旋轉彈箭在非線性靜力矩和馬格努斯力矩作用下的振幅平面方程，給出了形成穩定極限圓錐運動的判據條件以及極限圓錐運動幅值和頻率表達式，并結合攻角方程數值計算結果驗證了所得判據條件的有效性。但研究發現文獻[6]中給出的彈箭極限圓錐運動判定條件在一定條件下并不成立，且相關判據以及極限圓錐運動幅值和頻率表達式不夠明確(不能根據攻角方程中含有的參數，直接判斷極限圓錐運動的穩定性，并計算極限圓錐運動幅值和頻率)，這很大程度上限制了相關成果的適用范圍。

針對現有理論的不足，本文結合文獻[6]的相關研究成果，通過對彈箭在準圓運動狀態下的振幅平面方程進行泰勒展開，并分不同情況對方程解的存在性和穩定性進行詳細分析。在此基礎上，分析了同時在非線性靜力矩和非線性馬格努斯力矩作用下，彈箭形成穩定極限圓錐運動的必要條件，給出了相應的解析判據，并以某型旋轉尾翼彈為例進行算例分析，驗證了理論模型的正確性。

1 穩定極限圓錐運動形成條件分析

1.1 非線性攻角方程改進擬線性解

旋轉彈箭在非線性靜力矩和非線性馬格努斯力矩作用下的齊次攻角方程為

Δ″+(H-iP)Δ′-(M+iPT)Δ=0，

(1)

式中：H為俯仰阻尼力矩系數；P為陀螺穩定項，其值主要由彈箭滾轉速度及轉動慣量決定；M為靜力矩系數，M=M0+M2δ2，δ為攻角，M0為靜力矩系數線性項，M2為靜力矩系數非線性項；T為馬格努斯力矩系數，T=T0+T2δ2，其中T0為馬格努斯力矩系數線性項，T2為馬格努斯力矩系數非線性項。各參數的具體計算式可參見文獻[6]。

文獻[6]采用改進擬線性代入法對(1)式進行了推導求解，得到了旋轉彈箭在非線性靜力矩和非線性馬格努斯力矩作用下做準圓運動時的振幅平面方程，即

(2)

此時對應的彈箭做準圓運動時的頻率為

(3)

(4)

(5)

在實際研究中，已對上述公式推導過程的正確性做了充分的驗證，為節約篇幅，本文不再對上述表達式的推導過程作詳細介紹，而是在其基礎上，對旋轉彈箭形成穩定極限圓錐運動的判據作進一步分析。

1.2 非零奇點存在性條件

(6)

于是，彈箭準圓運動振幅平面方程(2)式的第1式可表示為

(7)

(8)

(9)

當PT2≠0時(包括PT2<0、PT2>0兩種情況)，由(9)式可得

(10)

(11)

進一步對(9)式進行整理得

(12)

當M2≠0時，有m2=M2/0≠0，將代入(12)式可得

(13)

令A=PT2/(H0m2)、B=P(2T0-H0)/(2H0)，則(13)式可簡化為

(14)

對(14)式左右平方，并進行整理，可得

(15)

當彈箭形成穩定極限圓錐運動時，要求(15)式具有實數解，即必須有

(2AB+0)2-4A2(B2+0)>0，

(16)

0(4AB-4A2+0)>0.

(17)

將A和B表達式代入(17)式，可得

(18)

當滿足(11)式、(18)式時，可得(8)式的解為

mc=mc1或mc=mc2，

(19)

式中：

1.3 非零奇點的穩定性條件

(20)

(21)

(22)

(23)

由此解得

(24)

(25)

(25)式成立的條件為

(26)

(27)

2 穩定極限圓錐運動形成判據

旋轉彈箭形成穩定極限圓錐運動需要同時滿足奇點存在性和穩定性兩方面的條件，當PT2≠0且M2≠0時，即需同時滿足(11)式、(18)式、(24)式以及(27)式。下面通過進一步分析，給出PT2和M2的不同取值情況下，旋轉彈箭穩定極限圓錐運動判據。

2.1 PT2<0且M2≠0情況

由(11)式中的第1式和(27)式可得

(28)

由(28)式可知，當H0≤0時，此不等式時不成立，因此必須有H0>0，于是(28)式可進一步解得

(29)

由(29)式可知，當PT2<0，必有H0>0是形成穩定極限圓錐運動的必要條件。

對(24)式進行整理得

(30)

將(30)式與(29)式聯立，可得

(31)

由(31)式可解得

(32)

綜上所述，當PT2<0時，彈箭在非線性馬格努斯力矩和非線性靜力矩作用下形成穩定極限圓錐運動的條件可表示為

(33)

式中：J1、J2、J3、J4、J5為便于分析所定義的5個判定參數，

此時有對應的極限圓錐運動幅值和頻率為

(34)

(34)式中mc即為由(19)式解出，且同時滿足(33)式所有判據條件的解。

2.2 PT2>0且M2≠0情況

由(11)式中的第2式可得

(35)

此時無法直接確定H0的符號，考慮到通常彈箭具有正阻尼，因此這里只考慮H0>0的情況。在此條件下，必有

(36)

由(24)式可得

(37)

由(37)式可以看出，當H0>0時，為使(37)式成立必須有M2<0，即T2和M2不能同時大于0，這是因為二者同時大于0時，靜力矩和馬格努斯力矩非線性項均是促使攻角幅值增大的，此時無法形成穩定的極限圓錐運動。由(37)式還可以解得

(38)

由(35)式與(38)式聯立可得

(39)

為使(39)式成立，必有

(40)

由此可解得

(41)

綜上所述，結合(18)式、(24)式、(35)式及(41)式可得，當H0>0且PT2>0時，彈箭在非線性馬格努斯力矩和非線性靜力矩作用下形成穩定極限圓錐運動的條件可簡化為

(42)

式中：Q1、Q2、Q3、Q4為判定參數，

此時，對應的極限圓錐運動幅值和頻率為

(43)

式中：mc即為由(19)式解出，且同時滿足(42)式所有判據條件的解。

2.3 PT2=0且M2≠0情況

由(11)式中的第3式可得

(44)

(45)

(46)

(44)式代入(46)式可得

(47)

進一步對(44)式進行求解，可得

(48)

(49)

(48)式代入(3)式可得由3次方靜力矩引起的極限圓錐運動頻率為

(50)

由(50)式可知，當僅考慮靜力矩非線性時，極限圓錐運動頻率表達式可化為極為簡單的形式。

綜上所述，旋轉彈在3次方非線性靜力矩作用下，形成穩定極限圓錐運動的條件為

(51)

由(51)式可知，正阻尼(H0>0)以及負的3次方靜力矩系數(M2<0)是形成穩定極限圓錐運動的必要條件。

2.4 M2=0情況

當僅考慮馬格努斯力矩非線性時(M2=0，T2≠0)，這種情況相對簡單，為節約篇幅這里不做詳細推導。采用與2.3節相似推導過程可得，此時存在穩定極限圓錐運動的條件為

(52)

相應地，可得到形式較為簡單的極限圓錐運動幅值和頻率表達式：

(53)

2.5 綜合判據

由(33)式和(42)式可知，無論PT2<0或PT2>0時，為形成穩定極限圓錐運動都需要滿足兩條完全相同的判據條件，即

(54)

對于PT2=0的情況，將T2=0代入(54)式，可得

(55)

由(55)式可知，當PT2=0時，J1>0恒成立，由J2>0可解得M2<0，這與(51)式給出的判據是一致的。因此，對于PT2<0、PT2>0以及PT2=0的情況，(54)式均是形成穩定極限圓錐運動的必要條件，故定義(54)式為綜合判據。

由(54)式可知，判據J2為關于T2和M2的線性函數，J1可視為關于(T2/M2)的2次函數，且當0<0時，J1關于(T2/M2)的函數圖像是開口向上的2次曲線，當0>0時，J1關于υ=T2/M2的函數圖像是開口向下的2次曲線，利用相關性質可對彈箭極限圓錐狀態進行判斷。

3 算例分析

為檢驗所得理論判據的有效性，以某型旋轉尾翼彈氣動及結構特征參數作為基本參數，以3次方馬格努斯力矩系數T2作為分析變量，對旋轉彈箭極限圓錐運動特性進行算例分析，基本參數如表1所示。

表1 基本參數

由2.4節可知，無論T2取何值(M2≠0時)，彈箭形成極限圓錐運動時，均需滿足綜合判據(54)式。為直觀分析判據J1和J2隨T2對的變化規律，首先，按表1對其余氣動參數進行取值，并由(54)式作出J1和J2關于T2的變化曲線，以確定使判據J1>0和J2>0同時成立時，T2所需滿足的取值范圍。在此基礎上，計算T2在不同取值下其余判據的取值，并預測極限圓錐運動形成情況。最后，將所選取參數組合代入攻角方程，并采用龍格庫塔法進行直接求解，以檢驗理論模型的正確性。

考慮到當M2和0取不同值時，判據J1>0和J2>0解的性質具有一定差異，因此對3種情況進行分析。

3.1 M2<0與0<0情況

圖1給出了按表1參數進行取值時，判據J1和J2隨T2的變化曲線，此時，有M2=-0.35<0，P(2T0-H0)=0.038>0，0=M0-P2/4=-0.019 5<0. 由圖1可知，當T2<1.152或T2>1.562時，判據J1>0成立，當T2<1.326時，判據J2>0成立，為保證J1>0、J2>0同時成立，須有T2<1.152，這是形成穩定極限圓錐運動的必要條件。

圖1 判據J1和J2曲線(M2<0，0<0)Fig.1 Curves of criteria J1 and J2 for M2<0 and 0<0

其余參數保持不變，T2分別取-2.00、-1.00、0、1.15、1.16、1.60. 一方面，根據T2的不同取值，分別由(33)式、(42)式及(51)式計算各判據條件，結果如表2所示。表2中當T2≠0且J1>0時，mc存在兩個可能的取值，即mc1和mc2，其值由(19)式給出。分別將mc=mc1和mc=mc2代入(33)式和(42)式，可得J3、J4及J5(或Q3、Q4及Q5)，進而判斷mc1和mc2中是否存在完全滿足所有判定條件的解。若存在，則將相應的mc值代入(34)式和(43)式中，得到由理論預測的極限圓幅值Kc和頻率φ′c. 表2中狀態項T表示形成了極限圓錐運動，F表示未形成極限圓錐運動。另一方面，將表1和表2給出參數代入攻角方程，并采用龍格庫塔法對攻角方程進行迭代求解，得到T2取不同值時的攻角曲線，結果如圖2所示。

對比表2和圖2可知，在不同T2取值下，數值計算結果與表2預測結果完全一致，即當T2<1.152時，彈箭形成了穩定極限圓錐運動，而當T2>1.152時，彈箭攻角發散，未形成穩定極限圓錐運動，其中，T2=1.15的攻角曲線變化規律已達到臨界狀態(即將發散)，而當T2=1.16時，攻角曲線已出現發散，表明本文給出的穩定極限圓錐運動判據具有很高的靈敏度。由表2的結果可知，當T2=1.60時判據J1>0，存在兩個可能的奇點位置，分別對應mc=mc1和mc=mc2，但這兩個奇點位置均不能使其余判據完全成立，故不能形成穩定極限圓錐運動。由此說明，判據J1>0是保證攻角方程奇點存在性的必要條件，而其余判據則是保證奇點為穩定結點的必要條件，在對彈箭極限圓錐運動狀態進行預測時，必須對所有判據進行檢驗。此外，對比算例T2=-1.00、T2=0、T2=1.15的結果可知，極限圓錐運動幅值和頻率均隨3次方馬格努斯力矩系數T2增加而增大。

表2 極限圓錐運動驗證算例(M2<0，0<0)

Tab.2 Example for verification of limiting conical motion (M2<0，0<0)

表2 極限圓錐運動驗證算例(M2<0，0<0)

T2J1J2其他判定條件狀態mcδcφc-1.001.8×10-38.8×10-3mc1=12.6、J3=-0.42、J4=1.8、J5=0.14Fmc2=1.33×10-2、J3=8.0×10-4、J4=0.32、J5=0.23T1.33×10-21.740.20706.0×10-45.0×10-3^M0+[P(2T0-H0)]2/4H20=5.5×10-3T2.330.2081.153.6×10-77.0×10-3mc1=0.428、Q3=2.8×10-2、Q4=-2.7×10-3Fmc2=0.296、Q3=2.0×10-2、Q4=2.9×10-3T0.2968.240.2281.16-9.9×10-76.0×10-4F1.605.7×10-6-1.0×10-3mc1=-0.153、Q3=-1.4×10-2、Q4=-1.4×10-2Fmc2=-0.427、Q3=-4.0×10-2、Q4=1.7×10-3F

圖2 不同T2下的攻角曲線(M2<0，0<0)Fig.2 Angle-of-attack curves with different T2 for M2<0 and 0<0

3.2 M2<0與0>0情況

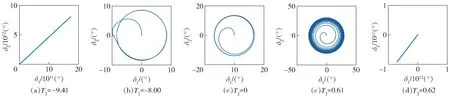
圖3給出了當M0=0.01，其余參數按表1取值時，判據J1和J2隨T2的變化曲線，此時M2=-0.35<0，0=M0-P2/4=0.007 5>0，且有P(2T0-H0)=0.038>0. 由圖3可知，當-9.4880成立，當T2<1.326時判據J2>0成立，為保證J1>0、J2>0同時成立，須有-9.488

圖3 判據J1和J2曲線(M2<0，0>0)Fig.3 Curves of criteria J1 and J2 for M2<0 and 0>0

其余參數保持不變，T2分別取-9.49、-9.48、-9.41、-8.00、-1.00、0、0.61、0.62，按(33)式、(42)式及(51)式進行分析計算，結果如表3所示。按表1和表3給出參數代入攻角方程，并采用龍格- 庫塔法對攻角方程進行迭代求解，得到T2取不同值時的攻角曲線，部分結果如圖4所示。

表3 極限圓錐運動驗證算例(M2<0，0>0)

Tab.3 Example for verification of limiting conical motion for M2<0 and 0>0

表3 極限圓錐運動驗證算例(M2<0，0>0)

T2J1J2其他判定條件狀態mcδcφc-9.49-3.4×10-74.1×10-2F-9.486.3×10-74.1×10-2mc1= -1.05、J3=0.14、J4=-2.8×10-2、J5=2.0Fmc2= -1.08、J3=0.13、J4= -1.6×10-2、J5=1.8F-9.417.3×10-64.1×10-2mc1= -1.03、J3=0.14、J4=-4.1×10-2、J5=2.4Fmc2= -1.12、J3=0.13、J4= -9.0×10-4、J5=1.6F-8.001.2×10-43.5×10-2mc1= -1.02、J3=0.14、J4=-4.5×10-2、J5=2.5Fmc2= -1.56、J3=9.3×10-2、J4= 9.8×10-2、J5=1.1T-1.5610.490.115-1.001.3×10-48.8×10-3mc1= -2.64、J3=4.7×10-2、J4=0.24、J5=0.29Tmc2= -38.6、J3=-0.37、J4= 1.6、J5=0.14F-2.6413.640.16105.6×10-55.0×10-3^M0+[P(2T0-H0)]2/4H20=3.3×10-2T-4.3417.480.2080.619.5×10-72.7×10-3mc1=-12.96、Q3=0.14、Q4=9.1×10-3Tmc2=-21.17、Q3=0.23、Q4=-7.0×10-3F-12.9630.200.3500.62-1.6×10-82.7×10-3F

圖4 不同T2下的攻角曲線(M2<0，0>0)Fig.4 Angle-of-attack curves with different T2 for M2<0 and 0>0

3.3 M2>0與0>0情況

圖5為當取M0=0.01、M2=0.35>0，其余參數按表1進行取值時，判據J1和J2隨T2的變化曲線，此時0=M0-P2/4=0.007 5>0，且有P(2T0-H0)=0.038>0. 由圖5可知，無論T2取何值，均不能使判據J1>0、J2>0同時成立，即在此條件下，無法形成穩定極限圓錐運動。其余參數保持不變，T2分別取-1.0、-0.5、0、1.0對攻角方程進行求解計算，結果表明(見圖6)，數值計算結果與理論分析結果是一致的，即在本文選取的參數條件下，當M2>0、0>0時，T2無論取何值均無法形成穩定極限圓錐運動。

圖5 判據J1和J2曲線(M2>0，0>0)Fig.5 Curves of criteria J1 and J2 for M2>0 and 0>0

圖6 不同T2下的攻角曲線(M2>0，0>0)Fig.6 Angle-of-attack curves with different T2 for M2>0 and 0>0

4 結論

本文通過對彈箭在準圓運動狀態下的攻角運動振幅平面方程，進行泰勒展開處理，進而對其非零奇點的存在性和收斂性進行了分類討論，得到了不同參數條件下，彈箭形成穩定極限圓錐運動的判據條件，及其極限圓錐運動幅值和頻率表達式，并以某型旋轉尾翼彈參數為例對相關結果進行了驗證。通過上述研究，得出以下結論：

1)本文給出的判據條件與現有研究相比具有更明確的解析關系，且所考慮的參數范圍更為全面。算例分析結果表明，本文推導得到的旋轉彈箭在非線性馬格努斯力矩和非線性靜力矩作用下形成極限圓錐運動的判據條件，能準確預測彈箭極限圓錐運動形成情況，驗證了理論模型的正確性。

2)當M2≠0時，對于PT2<0、PT2>0以及PT2=0的情況，彈箭形成穩定極限圓錐運動均需滿足本文給出的僅與攻角方程初始參數有關的兩條綜合判據條件J1>0和J2>0. 雖然判據J1>0和J2>0僅是形成穩定極限圓錐運動的必要條件，但算例分析結果顯示，當攻角方程各參數滿足這兩條判據時，在大多數情況下彈箭均會形成穩定極限圓錐運動，根據這兩條判據可方便快捷地對彈箭的極限圓錐運動特性進行初步判斷。

3)對于本文分析的4種參數取值情況均有僅當T2和M2中至少一個為負值時，才可能形成穩定極限圓錐運動，這是因為正的T2和M2均是促使角運動發散的因素，當二者均為正時彈箭準圓運動無法收斂。此外，對于PT2<0且M2≠0、PT2=0且M2≠0、M2=0 3種情況均可由理論推導嚴格證明具有正阻尼H0>0是旋轉彈箭形成穩定極限圓錐運動的必要條件，而對于PT2>0且M2≠0這一情況無法嚴格證明這一結論，因此本文結合掠飛靈巧彈藥氣動特性，在假設H0>0的條件下，推導了穩定極限圓錐運動形成判據。