鍋爐水循環系統的無模型自適應控制研究
朱明山,劉劍敏,胡小虎,余 數,徐順寵,葉志暉
(浙江中煙工業有限責任公司 寧波卷煙廠, 浙江 寧波 315504)
如何提高鍋爐熱效率是動力供應部門需要面對的重要問題。目前,鍋爐余熱回收控制系統在PID控制算法基礎上有所發展。李素真等[1]采用監督預測控制算法對余熱鍋爐建立燃料量對主蒸汽壓力的控制模型,實現了階梯式控制策略,提高了控制速度。付一鳴等[2]采用線性擴張觀測器對余熱鍋爐水位二階化系統總擾動進行實時估計與補償,設計了具有串級形式的自抗擾控制器,實現了水位誤差快速收斂。顧蓉等[3]在PID反饋控制的基礎上加入自適應變參數的前饋控制,用于控制干熄焦余熱鍋爐的主蒸汽溫度,取得了較好的效果。王曉明等[4]提出了帶擾動補償控制的無模型自適應控制算法,將其應用于鍋爐汽包水位控制系統,克服了汽包水位系統中蒸汽流量的外在擾動,實現了無靜差控制。無模型自適應控制(MFAC)算法[5]是一種典型的數據驅動控制算法,利用被控系統的輸入輸出數據設計出性能穩定的控制器。MFAC由于其高效的控制性能被應用于許多領域。文獻[6]提出了一種新穎的無模型自適應控制算法,用于多輸入多輸出非線性的離散系統控制。為提高高速無刷直流電機系統的可靠性、降低功耗,文獻[7]給出了一種基于無模型自適應控制(MFAC)的無位置傳感器的驅動器,能夠在整個運行速度范圍內獲得理想的整流效果。文獻[8]將滑模控制和無模型自適應控制相結合用于離散非線性過程控制中,確保了跟蹤誤差的快速收斂性。文獻[9]引入非周期神經網絡權值更新法估計無模型自適應控制器參數,應用于非線性離散系統的事件觸發數據驅動控制問題。文獻[10]將神經網絡模型辨識和無模型自適應控制相結合應用于碳捕獲過程控制中,有效地將排放源產生的二氧化碳收集起來。但是該控制算法有4個參數需要人工設定,這會影響控制算法的性能。針對以上情況,很多國內學者對其參數進行了優化。黃偉[11]采用改進的人工魚群算法對無模型自適應控制算法進行參數優化。楊延西[12]利用量子粒子群優化對無模型自適應控制算法控制參數尋優,確定了控制參數。費盛[13]通過遺傳算法對無模型自適應控制算法進行參數優化。馮增喜[14]采用單純形法實現了MFAC參數尋優設計。然而,這些優化算法過于復雜,需要進行大量的額外運行,不適合在控制系統中應用。模式搜索法優化具有簡單、快速收斂的優點,鑒于此,本文采用模式搜索法優化無模型自適應控制算法的4個參數,使其控制性能達到最優,然后用于鍋爐余熱控制系統中,以求最大限度地利用燃料熱量提高鍋爐熱效率。
1 問題分析
吸收鍋爐尾部煙氣的熱量是提高鍋爐熱效率的有效措施,其主要過程是在鍋爐排煙線路上安裝煙氣熱交換器,采用低溫軟水去吸收煙氣換熱器的多余熱量后流入到保溫水箱,回收的熱水可再次用作鍋爐補水,既提高了鍋爐的補水溫度,又降低了排煙溫度,實現了提高鍋爐熱效率、降低產品生產成本和節能環保的目的。換熱器的軟水流動性直接影響熱交換的效率,阻礙軟水流動性的原因在于:軟水從鍋爐軟水箱進入換熱器被加熱,再到保溫水箱,當保溫水箱液位到達設定值時,為避免保溫水箱中軟水溢出,軟水供應會停止,從而導致換熱器中無軟水流動,使部分軟水在換熱器中滯留,被過度加熱而引發安全隱患,且不能充分吸收尾部煙氣熱量。
為進一步提高鍋爐給水溫度,降低排煙溫度,提高鍋爐熱效率,節省企業生產成本,根據設定的目標對鍋爐給水系統及尾部煙氣余熱回收系統進行方案優化,對可能的方案進行研究論證,并最終對鍋爐水循環系統進行改造安裝。
改造后的鍋爐水循環系統如圖1所示。為充分吸收鍋爐尾部煙氣的熱量,用鍋爐軟水箱到保溫水箱的低溫軟水去吸收這部分熱量。軟水從鍋爐軟水箱進入換熱器被加熱,再到保溫水箱,當保溫水箱液位到達設定值時,為避免保溫水箱中軟水溢出,軟水供應會停止,從而導致換熱器中無軟水流動,使部分軟水在換熱器中滯留被過度加熱而引發安全隱患,也影響尾部煙氣熱量的充分吸收。因此,在保溫水箱進口處設電動三通閥,利用保溫水箱液位通過PID控制軟水送回軟水箱的流量,及時調整保溫水箱進水調節閥開度,以保證軟水的流動性和煙氣熱量的充分吸收。
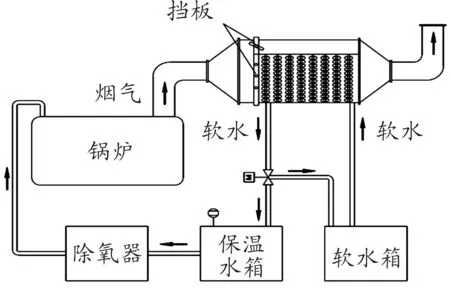
圖1 改造后的鍋爐水循環系統
目前,保溫水箱的進水調節閥采用PID控制算法。受系統時滯和非線性等因素影響,常規PID控制器進行保溫水箱進水閥調節時容易出現初期流量超調和后期控制精度低等問題。為了進一步實現精確控制,本文建立了一種基于模式搜索優化的無模型自適應控制方式,提高了保溫水箱進水閥的控制能力,提升了鍋爐余熱利用率。
2 設計方法
2.1 系統辨識
本文的鍋爐水循環系統是一個單輸入單輸出非線性系統,輸入量是保溫水箱的液位,輸出量是進水調節閥開度,輸入量和輸出量之間有如下關系:
y(k)=f(y(k-1),…,y(k-ny),
u(k-1),…,u(k-nu))
(1)
在控制之前,需要對保溫水箱的液位和進水閥開度數據進行系統辨識,以得到被控對象的模型。
由于保溫水箱的液位和進水閥開度是工藝過程數據,產生的數據量比較大,而且需要快速得到輸入輸出之間的關系,因此本文采用收斂較快的批量最小二乘法進行系統參數辨識。
將式(1)寫成如下最小二乘形式:
y(k)=-a1y(k-1)-…-anay(k-na)+
b1u(k-1)+…+bnbu(k-nb)+ξ(k)=
φT(k)θ+ξ(k)
(2)
式中:φ(k)為數據矢量;θ為待估計參數矢量,即
φ(k)=[-y(k-1),…,-y(k-na),
u(k-1),…,u(k-nb)]T
θ=[a1,…,ana,b1,…,bnb]T
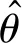
(3)
式中:Y=[y(1),y(2),…,y(M)]T∈RM×1;Φ=[φT(1),φT(2),…,φT(M)]T∈RM×(na+nb+1)。
2.2 無模型自適應控制
對于保溫水箱的液位和進水閥開度模型,本文采用無模型自適應控制的緊格式動態線性化方法(CFDL)進行控制。該模型關于控制輸入u(k)的偏導數是連續的,因此式(2)可以等價表示為如下CFDL模型:
y(k+1)=y(k)+Δy(k+1)=
y(k)+φ(k)Δu(k)
(4)
式中:Δy(k+1)=y(k+1)-y(k);φ(k)為偽偏導數。
接著,定義一個控制性能指標函數:
J(u(k))=[yr(k+1)-y(k+1)]2+
λ[u(k)-u(k-1)]2
(5)
式中:yr(k+1)為期望輸出信號;λ>0為權重因子。
將式(4)代入式(5),得到新的指標函數:
J(u(k))=[yr(k+1)-y(k)-
φ(k)(u(k)-u(k-1))]2+
λ[u(k)-u(k-1)]2
(6)
可見,u(k)影響了指標函數J(u(k))的性能。為了得到最佳的u(k),用J(u(k))對u(k)求導:
2(λ+φ(k)2)(u(k)-u(k-1))
(7)
為了得到最優的控制律,即求取上式的極值,令式(7)值為零:
-2φ(k)(yr(k+1)-y(k))+
2(λ+φ(k)2)(u(k)-u(k-1))=0
得到如下控制律:
(8)
為了使控制律更具有泛化性,另外加入參數ρ>0來調節控制律,則新的控制律變為
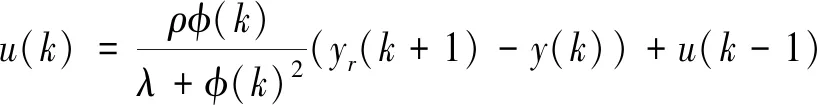
(9)
由于偽偏導數φ(k)一般是時變的,因此需要重新估計φ(k)的值。設計一個關于φ(k)的估計準則函數:
(10)
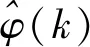
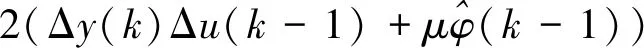
(11)
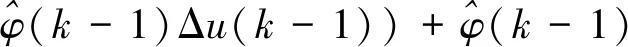
(12)
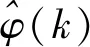
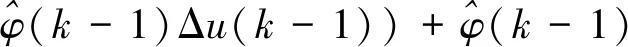
(13)
2.3 模式搜索優化算法
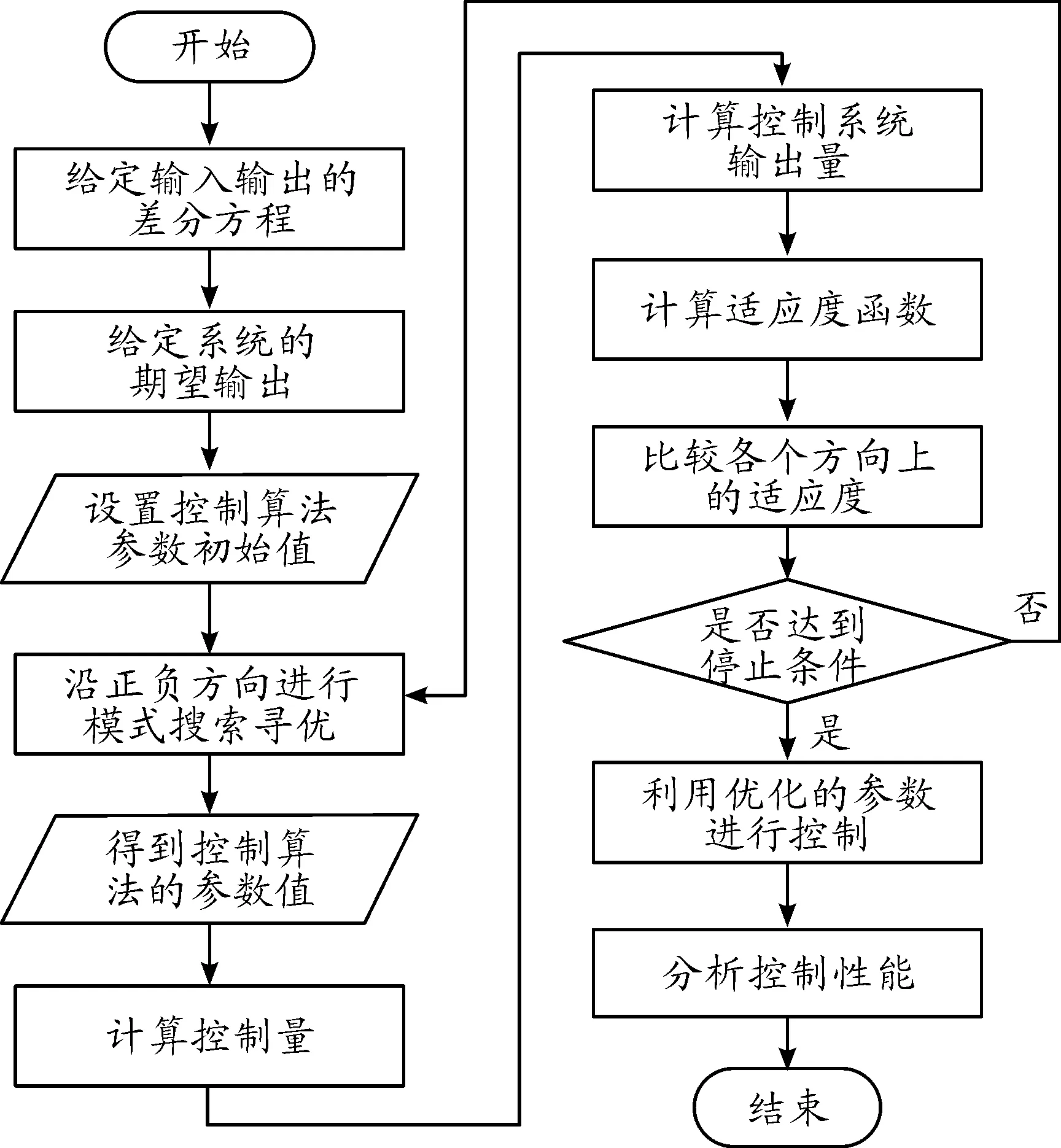
模式搜索算法是一種不依賴于導數的直接搜索算法,可求解不可微分或不連續的最優化問題,且計算速度較快,符合控制速度的要求。模式搜索算法主要由探測移動和模式移動兩種移動過程組成。探測移動主要探測使得目標函數下降的坐標位置,因此沿著坐標軸移動;模式移動用于找到兩個相鄰探測點之間的最優值,因此沿著兩個相鄰的探測點連線的方向移動,兩種移動方式交替進行。模式搜索算法原本用于多維無約束優化問題,由于需要優化的4個參數都是正數,因此只需要修改搜索算法,使其在正數范圍內搜索。下面是改進的優化模式搜索算法計算步驟:
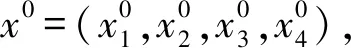
步驟2令y=xk。
步驟3從y出發,依次作平行于單位矢量ej(j=1,2,3,4)的軸向探測移動。
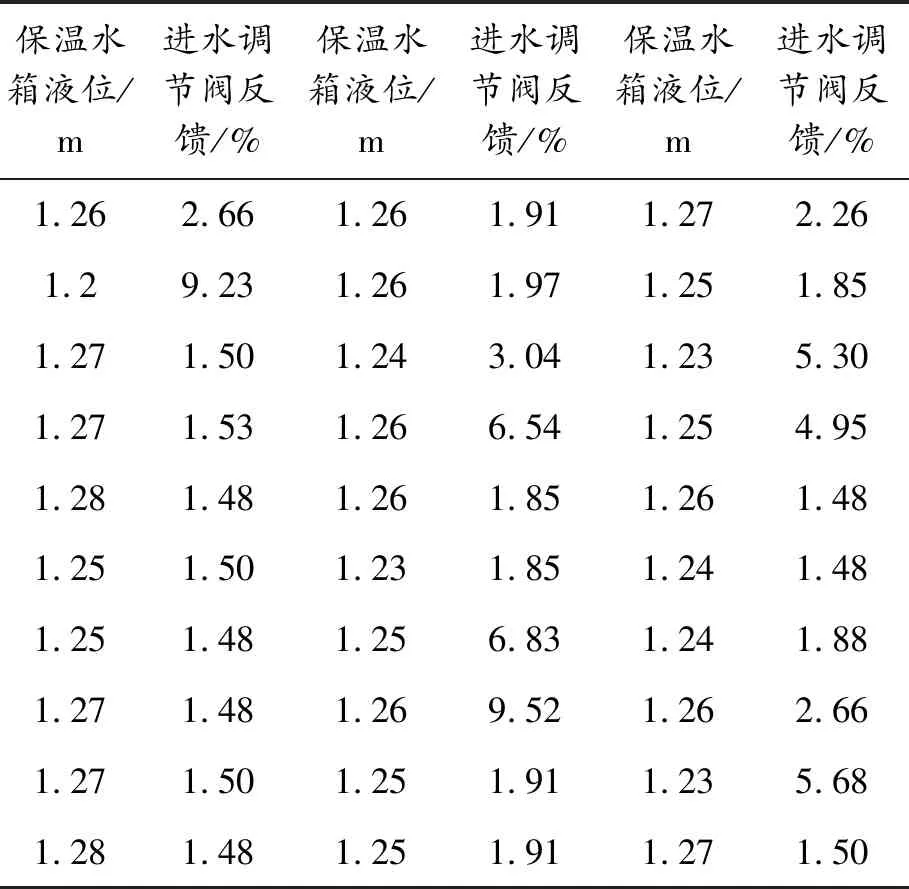
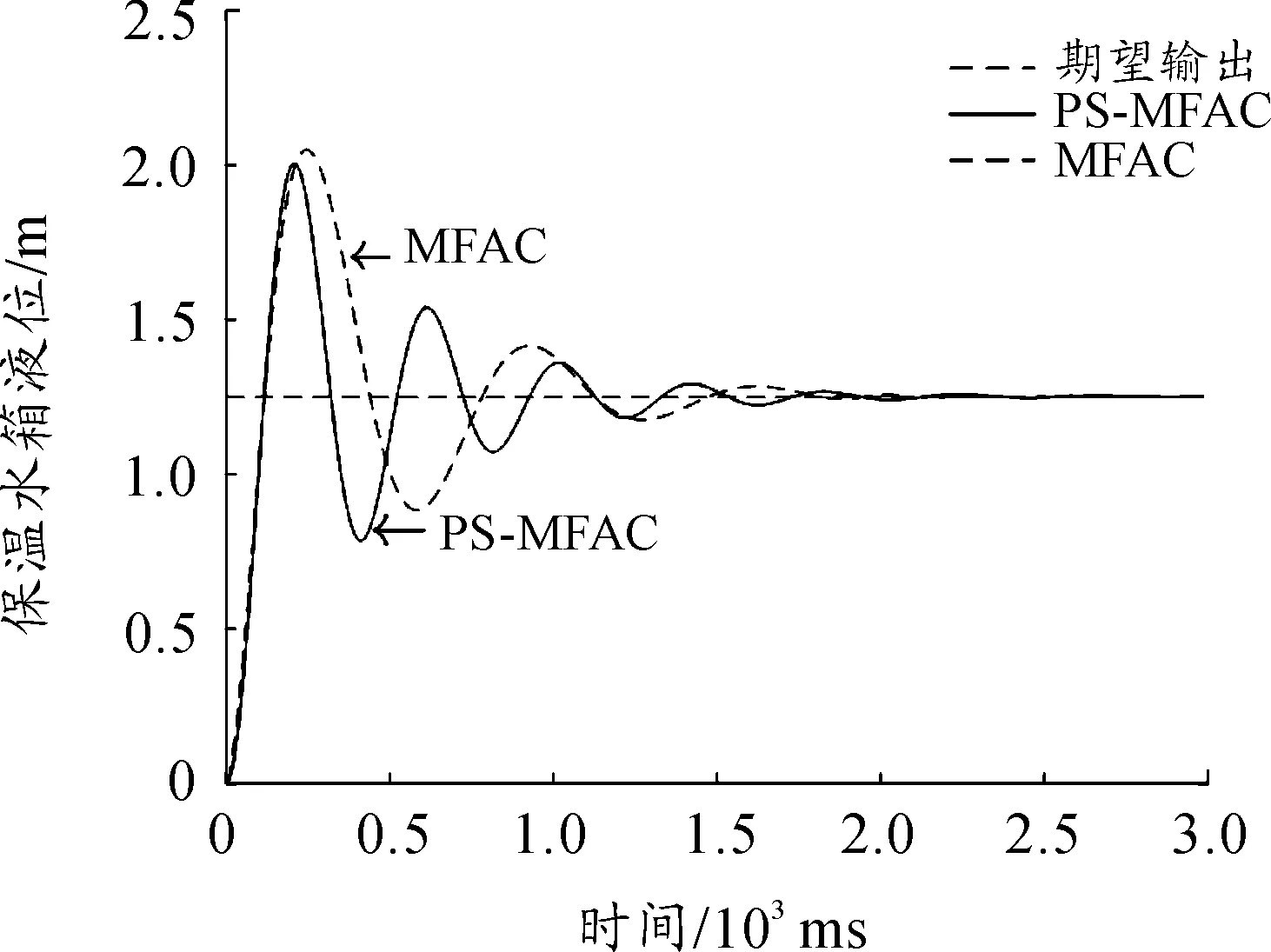
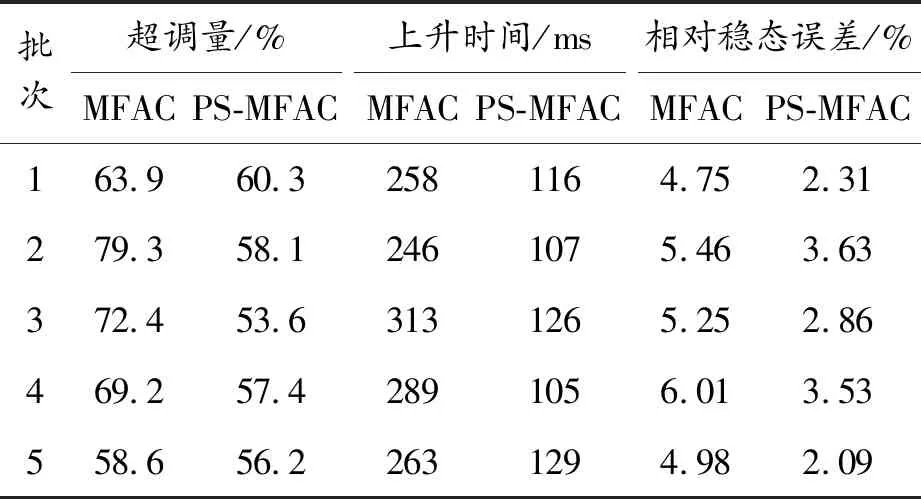
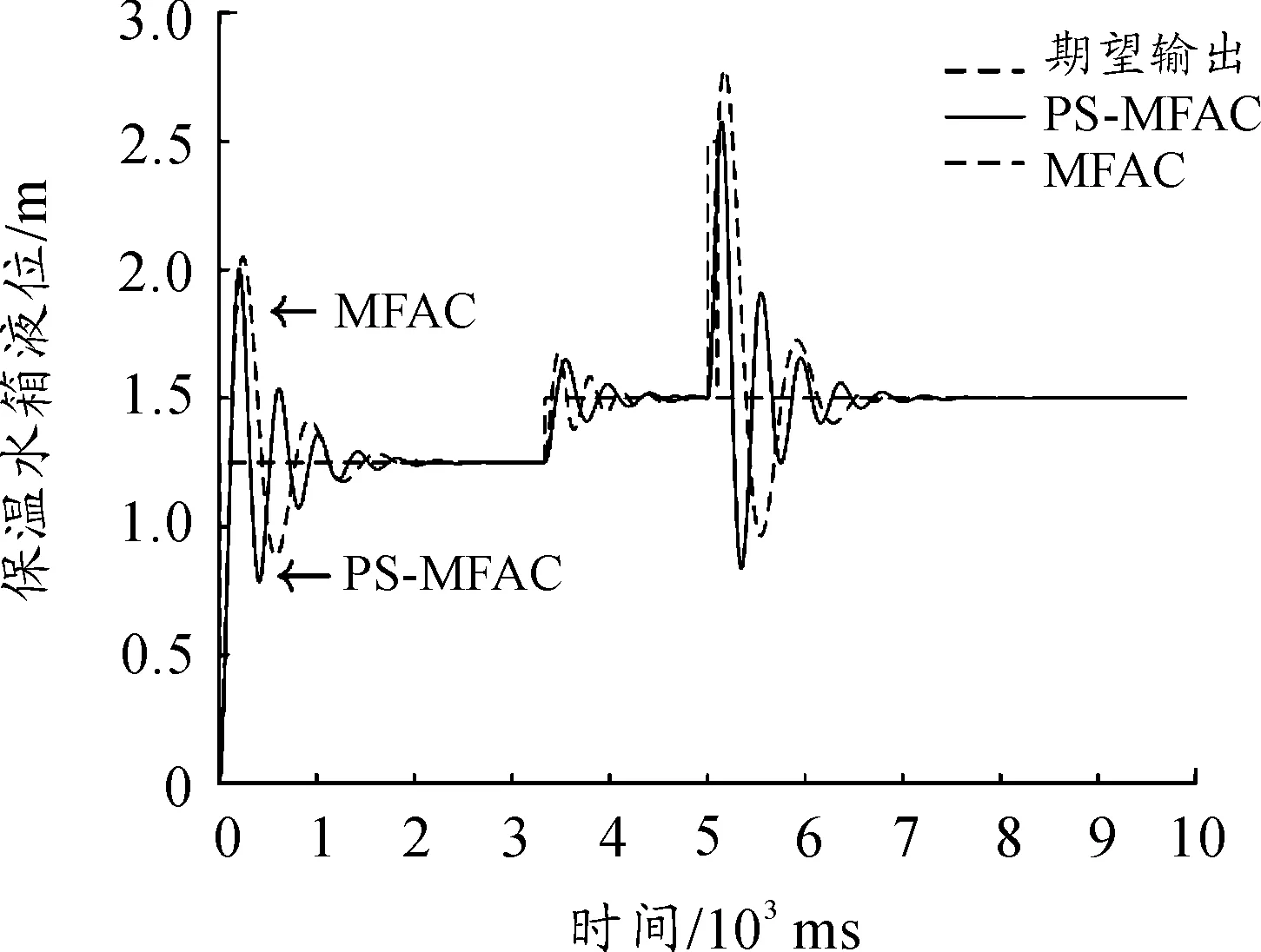
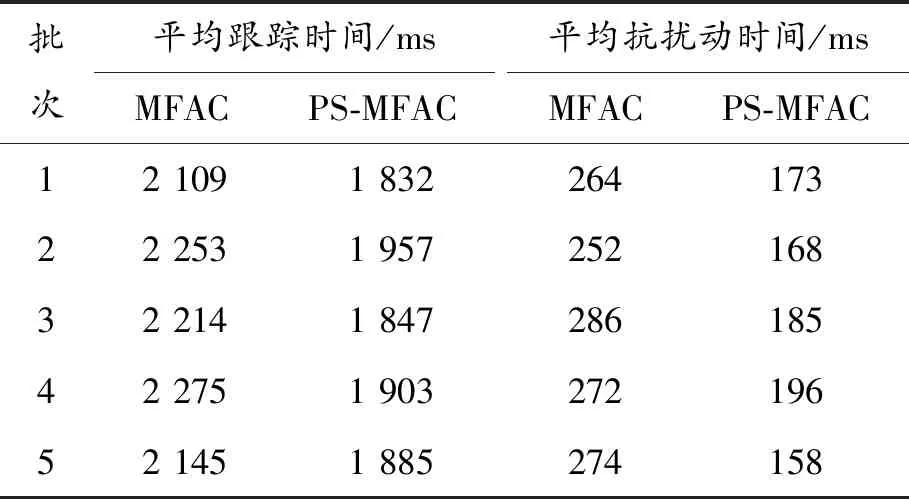
步驟4令xk+1=y,若f(xk+1) 步驟5若|δk|<ε或者k=iter,則停止迭代,輸出xk;否則當xk+1≠xk時,令y=xk+1,δk+1=δk,k=k+1,轉至步驟3,當xk+1=xk時,令y=xk+1δk+1=θδk,k=k+1,轉至步驟3。 為了尋找MFAC算法的最優參數,需設計一個適應度函數。該適應度函數應主要考慮控制誤差,其次應限制系統輸入和輸出的波動幅度,以避免在控制過程中出現過度震蕩。因此,本文設計了如式(14)的適應度函數。 F(ρ,λ,η,μ)=(yr(k+1)-y(k+1))2+ (u(k)-u(k-1))2+(y(k)-y(k-1))2 (14) 把模式搜索優化和無模型自適應控制相結合,整體尋優流程如圖2所示。由于模式搜索優化算法從初始值出發自動搜索尋優,因此一旦設置了MFAC的初始參數,在迭代過程中就不需要再設置初始值,這也是模式搜索算法的優點之一。 圖2 模式搜索尋優流程 采用OPC客戶端軟件對工藝數據進行實時采集,每1 s采集1次鍋爐保溫水箱的液位和進水調節閥反饋量,共收集5個批次數據,部分數據如表1所示。 表1 保溫水箱部分時段的工藝參數 首先,利用上述數據進行系統辨識,辨識算法即最小二乘法。取滯后時間為2 s,即na=2,nb=2,得到如式(15)所示的保溫水箱的液位和進水閥開度輸入輸出模型: y(k)=-0.603 2y(k-1)-0.390 5y(k-2)+ 0.002 2u(k-1)+0.000 8u(k-2) (15) 為便于比較控制算法性能,考慮到PID算法受參數整定的影響性能不穩定,采用兩種控制算法進行比較。兩種控制算法分別是標準的無模型自適應控制算法和本文提出的基于模式搜索優化的無模型自適應控制算法。 模式搜索優化的初始化值為:初始點x0={0.14,0.15,0.12,0.13},初始步長δ0={0.1,0.1,0.1,0.1},加速系數γ=1.4,收縮系數θ=0.2,精度ε=0.01,最大迭代次數iter=100。 標準的無模型自適應控制算法的4個參數{η,μ,ρ,λ}值為{0.34,0.65,0.82,0.53}。 3.3.1超調量 超調量σ是刻畫響應峰值和穩態值之間相對偏差程度的指標,σ越小表示系統震蕩越小。 (16) 式中:y(tp)為響應峰值;y(∞)響應穩態值。 3.3.2上升時間 上升時間τ是指響應曲線從穩態值的10%上升到90%所用的時間,τ越小表示響應速度越快。 3.3.3相對穩態誤差 相對穩態誤差e是響應曲線最終趨于穩定時系統響應和系統期望之間的相對偏差,e越小說明系統越穩定。 (17) 式中:yr為期望輸出;y(∞)為響應穩態值。 3.3.4平均跟蹤時間 平均跟蹤時間T(t1→t2)是系統從一個穩態過渡到新的穩態所需的時間總和的平均值。T(t1→t2)越小說明系統切換到新目標所需的時間越少。 3.3.5平均抗擾動時間 平均抗擾動時間T(v)是系統受擾動作用重新恢復平衡所用的時間總和的平均值。T(v)越小說明系統抗干擾性能越強。 首先分析對比2種控制算法的靜態性能指標:超調量、上升時間和相對穩態誤差。保溫水箱水位設定為1.25 m,比較2種控制算法的靜態性能。 圖3 兩種控制算法的響應曲線 批次超調量/%MFACPS-MFAC上升時間/msMFACPS-MFAC相對穩態誤差/%MFACPS-MFAC163.960.32581164.752.31279.358.12461075.463.63372.453.63131265.252.86469.257.42891056.013.53558.656.22631294.982.09 從圖3和表2可以看出:采用模式搜索優化的無模型自適應控制系統的靜態性能較高,有效地降低了超調量,縮短了上升時間,減少了相對穩態誤差。 接著對比2種控制算法的動態性能指標:平均跟蹤時間和平均抗擾動時間。為了進行跟蹤性實驗,在3 300 ms時增加鍋爐燃燒量,提高煙氣溫度,提高保溫水箱的水位設定值。為了進行抗擾動性實驗,在5 000 ms時,再次加大鍋爐燃燒量,由于煙氣溫度陡然升高,造成保溫水箱水位突然上升,控制系統對其做出恢復水位高度的控制處理,使其迅速回到設定的水位。 圖4 兩種控制算法的響應曲線 批次平均跟蹤時間/msMFACPS-MFAC平均抗擾動時間/msMFACPS-MFAC12 1091 83226417322 2531 95725216832 2141 84728618542 2751 90327219652 1451 885274158 從圖4和表3可以看出,采用模式搜索優化的無模型自適應控制系統動態性能更優,有效地降低了平均跟蹤時間和平均抗擾動時間。 無模型自適應控制是一種簡便而有效的控制策略,但由于其關鍵參數多憑經驗設定,在某些控制領域性能受到影響。在眾多的優化算法中,本文采用模式搜索算法進行參數優化,既搜索到了最優的參數值,又滿足了控制系統對速度的要求。這種優化控制策略被應用到鍋爐水循環控制回路中,首先采用批量最小二乘法辨識出鍋爐水循環系統中的保溫水箱部分的輸入輸出關系,然后采用基于模式搜索的無模型自適應控制算法通過保溫水箱進水閥調節保溫水箱的液位,提升了控制系統的靜態性能和動態性能,保證了鍋爐水循環系統的高效運行,提高了鍋爐余熱的回收效率。2.4 基于模式搜索優化的無模型自適應控制
3 仿真實驗
3.1 數據采集
3.2 控制算法參數選擇
3.3 控制指標選擇
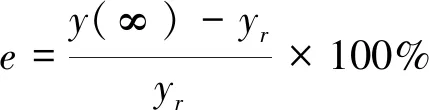
3.4 數據分析
4 結束語

