基于K最近鄰算法的城市路段行程時間短時預測
涂 銳,秦江靈,趙志平,徐建川,陳順舉,夏 立
(1.重慶市公安局渝北區分局交通巡邏警察支隊, 重慶 401120;2.重慶大學 計算機學院, 重慶 400044)
隨著經濟社會發展,我國各大中城市的汽車保有量近年開始急劇攀升,隨之帶來的環境污染、交通事故尤其是交通擁堵問題也日趨嚴重[1]。發展智能交通系統是解決城市道路交通擁堵、環境污染等問題的有效方法之一[2],而城市道路行程時間短時預測作為智能交通系統中的一個重要研究領域,能夠實現交通誘導,有效緩解城市道路的交通擁堵問題[3-4]。
短時交通流預測相關研究的數據來源主要包括GPS浮動車數據[5-6]、固定環形線圈檢測器數據[7]和汽車電子標識數據,但目前國內外的行程時間短時預測問題大多集中于基于GPS浮動車和固定環形線圈檢測器的數據,GPS浮動車只包含了出租車和公共汽車的數據但不包含,大量的私家車的出行數據,具有樣本量小的缺點。而固定環形線圈檢測器通常只部署在十字交叉路口,在空間上不具有廣泛性的特點。而對于汽車電子標識數據,多用于短時交通流預測的相關研究,具有一定的新穎性,同時由于包含了私家車在內的所有車輛的出行數據,具有樣本量大的優點,在空間分布上也具有廣泛性的特點。
短時交通預測的方法主要包括線性回歸模型[8](linear regressive)、時間序列模型[4](time series)、卡爾曼濾波模型[9](Kalman filtering),以及神經網絡模型[10-11](neural network)、組合預測模型[12-13](nonparammetric regress model)等,而K最近鄰(KNN)算法相比于以上方法的主要優點在于沒有復雜的參數估計,模型訓練時間短,適合處理海量歷史數據來實現實時預測。
目前已有文獻將KNN算法應用于短時交通流預測。Wenxin Qiao等[14]利用藍牙數據,將KNN算法與傳統的預測模型進行對比,并提出了改進的KNN-T模型。SH Lim等[15]利用高速公路收費數據,將KNN算法應用于行程時間的實時預測。Steve Robinson等[7]提出了KNN算法中選擇局部估計方法和k值的策略,并就提出的策略進行了實驗分析。
綜上可以發現:目前的研究大多基于GPS浮動車數據和固定環形線圈檢測數據,同時較少對城市道路進行相關研究。針對上述問題,本文提出了基于汽車電子標識數據和KNN算法的城市道路行程時間短時預測方法,重點研究了基于汽車電子標識數據的路段行程時間的估計和KNN算法中特征向量的構建。
1 基于汽車電子標識數據的路段行程時間估計
1.1 汽車電子標識數據采集
汽車電子標識(electronic registration identification of the motor vehicle,簡稱ERI)將車牌號碼等信息存儲在射頻標簽中,能夠自動、非接觸、不停車地完成車輛的識別和監控,是RFID技術在智慧交通領域的延伸[16]。RFID技術即射頻識別(radio frequency identification)技術[17],其工作原理為通過利用無線射頻方式進行非接觸式雙向通信的識別,以實現自我識別的功能。RFID技術具有高保密性、讀寫距離遠、可識別如汽車等高速運動的物體、能進行非接觸式雙向通信等優點,并且能在惡劣的環境下工作。目前,RFID技術與通信技術、互聯網技術等相結合,已大范圍應用于物聯網、智能交通和商品防偽等領域。
電子車牌是指安裝于機動車上具有電子信息識別功能和車牌數字號碼圖案的車牌標識,同時具有普通車牌和電子車牌的功能。將RFID技術應用到電子車牌中,相比于傳統的車牌具有能存儲信息、進行非接觸式自動識別、通過唯一的ID獲取車輛信息等特點。RFID電子車牌系統主要由標簽閱讀器(reader)、電子標簽(tag)以及交通信息中心3部分組成,見圖1。

圖1 RFID電子車牌系統
基于RFID電子車牌數據采集的工作原理是:將閱讀器部署在城市的主要交通干道,并與交通信息中心通過網絡相連接;當安裝有電子標簽的車輛進入到閱讀器的識別區域內時,電子標簽通過吸收閱讀器發出射頻的能源而變為激活狀態,激活后通過電子標簽內的天線采用某種調制方式將其攜帶的信息發射出去;閱讀器收到電子標簽發射的應答信號后,解碼其中的信息并將結果發送至交通信息中心。交通信息包含了車輛的電子標簽ID、車輛類別、車輛通過時間等信息,通過這些采集到的RFID電子車牌數據可以獲取到車流量、平均速度、行程時間等重要的交通流參數,為城市道路交通的研究提供了數據來源。
1.2 路段行程時間估計
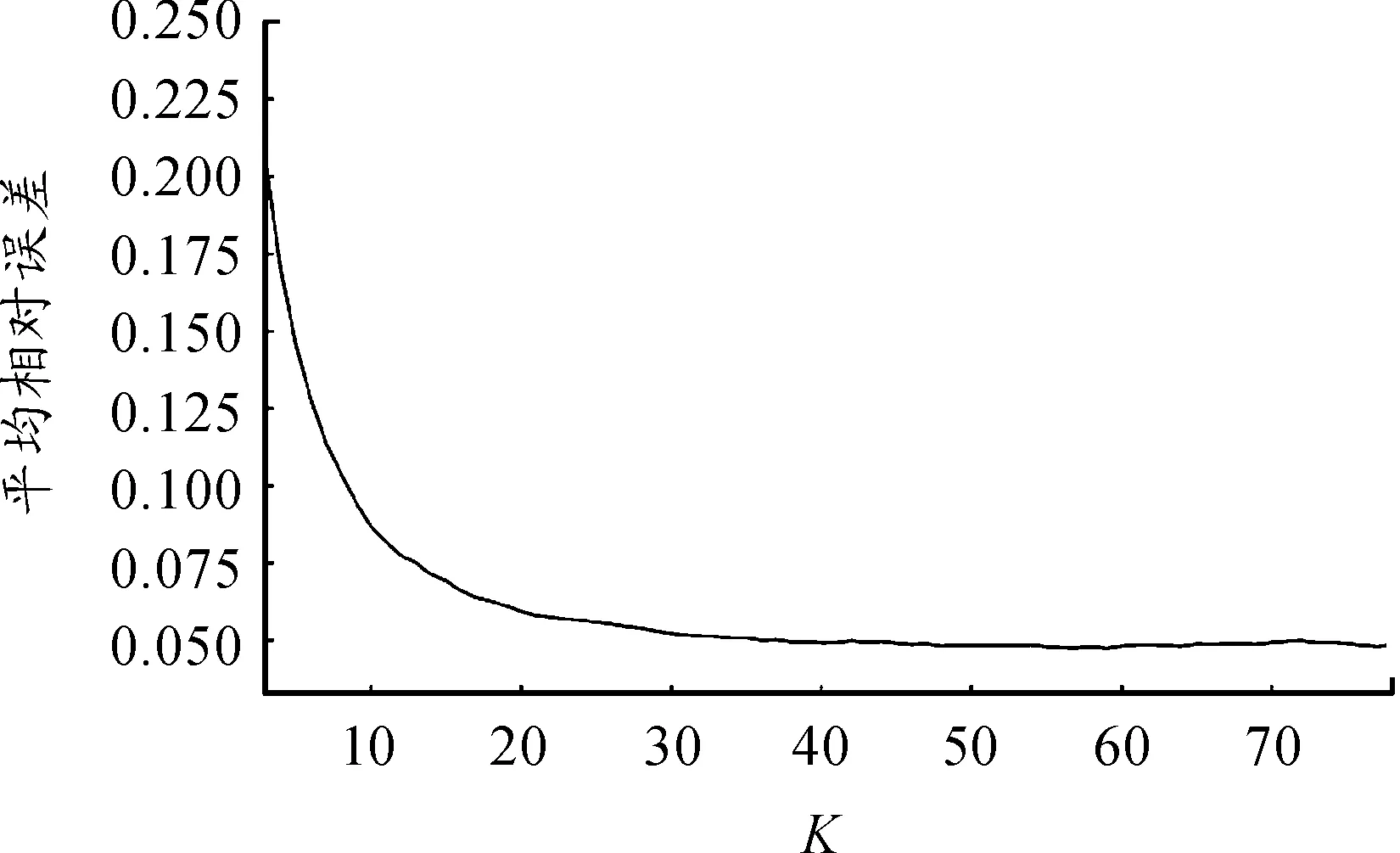
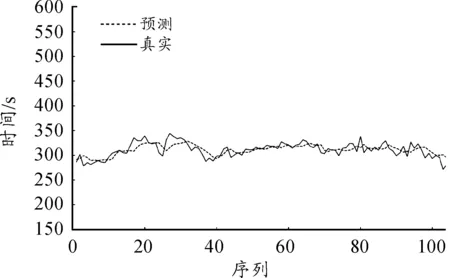
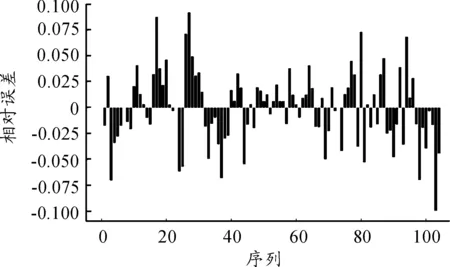
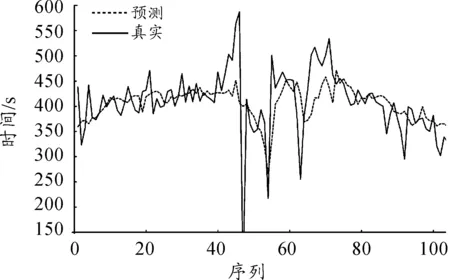
考慮圖2中在A、B兩個RFID采集點之間的道路,記為路段r。在觀測數據的一段時間間隔p內,車輛標識分別為i=1,…,N的共N輛車分別在時間為s1 {(si,Xi),i=1,…,N} (1) {(tj,Yj),j=1,…,M} (2) 在式(1)和(2)中,存在的Xi=Yj,則表明同一輛車x在一段時間p內通過了RFID采集點A和采集點B,用tj減去si的值即可得到車輛x通過路段r的行程時間Tx。對于式(1)和(2)中所有存在的Xi=Yj,執行上述操作即可得到時間段p內所有通過了路段r的行程時間,如式(3)所示。 {Tx=tj-si|Xi=Yj} (3) 設在式(3)中得到的車輛通過路段r的行程時間序列長度為L,即在時間段p內通過了路段r的車輛數目為L,因此得到了L個行程時間值的序列: {Tx,x=1,…,L} (4) 本文使用時間段p內所有通過路段r車輛的平均路段行程時間作為路段r在時間段p內的行程時間來估計Trp,即求式(5)中這L個值的均值,得到 (5) K最近鄰(KNN)算法的基本思想是:將當前輸入變量與具有相似輸入變量的歷史數據值相匹配,其中輸入變量通常稱為特征向量[14]。每個特征向量描述被稱為特征空間的多變量空間中的一個點,如果特征向量包含n個屬性值,則該特征空間是n維的。KNN算法的輸出值被定義為與輸入特征向量具有相似特征向量的已知輸出歷史記錄相關的函數。 設Yt是t時段的一個待求解的預測值,用Xt表示t時段的預測值所對應的特征向量。KNN算法中對于給定的輸入特征向量Xt,在歷史數據集中搜索與輸入特征向量Xt距離最近的K個歷史特征向量Xh1,Xh2,…,Xhk,然后將這K個特征向量通過加權估計的方法求解預測值Yt。 本文城市路段行程時間短時預測使用的數據集為重慶市的汽車電子標識數據。對于城市道路,在凌晨時的車流量較小,通常處于自由流狀態,因此沒有預測的必要。所以,預測的時間段選定為06∶00—23∶59。 設路段r為待進行路段行程時間預測的一條城市路段。根據路段r的歷史汽車電子標識數據,將一天的早上06∶00到凌晨00∶00共18 h,按每10 min作為一個時間段,即06∶00至06∶10作為一個時間段,06∶10至06∶20作為一個時間段,以此類推,共劃分為128個時間段。如果路段r有n天的歷史數據,那么共有n×128個歷史數據的時間段需要計算路段行程時間。然后計算路段r歷史數據在各個時間段的路段行程時間估計值,并將計算結果進行存儲。 特征向量的組成與路段行程時間需要有一定的相關性,同時能體現同一路段在不同時間的差異性,為了能夠滿足實時預測的需求,特征向量還需要能夠較容易地從歷史數據集中計算得出。由于交通流的特征,行程時間在時間序列中具有一定自相關性,所以一般都選擇當前時間段的前幾個時間段的路段行程時間作為特征向量的一部分。對于歷史時段p,選取p時段的前10個時間段(p-1,p-2,…,p-10)進行相關性分析,結果表明:當前時間段p與前4個時間段的相關性相對較高,因此選擇當前時間段的前4個時間段的行程時間(tp-1,tp-2,tp-3,tp-4)作為p時段的特征向量的一部分。 一段時間內通過RFID采集器的車流量也反映了當前的道路的通行情況,與當前道路的行程時間有極大相關性。對于一段道路兩端的2個采集點A、B,假設時間段p內(例如10 min內)通過采集點A、B的累計車流量分別為VA(p)和VB(p),則p時間段的前4個時間段內通過采集點A、B的車流量作為p時段特征向量的一部分。于是可以得到p時間段特征向量的表達式: [tp-1,tp-2,tp-3,tp-4,vA(p-1),vB(p-1),…, vA(p-4),vB(p-4)] (6) K值是KNN算法中的唯一參數,其值的選定直接關系到預測結果的準確性。本文采用交叉驗證的方式來確定最優K值,具體步驟如下: ① 選取K的最小值和最大值分別為Kmin和Kmax。 ② 將路段r的歷史數據集以天為單位隨機平均分為M份,得到數據集集合D1,D2,…,DM,然后依次將數據集Di(i=1,2,…,M)作為測試數據集,其他的M-1份數據集作為歷史數據集。 ③ 取K=K0,K0在最小值Kmin和最大值Kmax之間,計算測試數據集Di的平均絕對誤差百分比。 (7) 式中:Np為測試數據集中Di中的樣本量;Ar為測試數據集Di中第r條記錄的真實值;Ap是當K取值K0時,測試數據集Di中應用預測方法得到的預測值。 ④ 當K取K0時,分別按式(7)計算M個數據集對應的平均絕對誤差百分比,并對這M個值求均值: (8) 對于式(6)的特征向量,由于包括行程時間和車流量兩個不同維度的數據,因此采用歸一化的歐幾里德距離公式,將特征向量中的值歸一化到區間0~1。然后利用式(9)進行特征向量間的距離計算。 (9) 應用局部估計方法之前,首先在歷史數據中尋找與預測值的特征向量之間距離最近的K個特征向量,然后對這個特征向量所對應的值進行加權估計得到預測值。由于當歷史數據的特征向量與待預測值的特征向量更接近時,該歷史數據的行程時間對待預測值具有更大的影響,則通過加權的方式得到路段r在時間段p的路段行程時間預測值TP(p)。 (10) 式中:TP(p)為待要預測的路段行程時間值;TK(u)為K個鄰近歷史特征向量中特征向量Xu(u=1,2,…,k)所對應的路段行程時間值;ω(XP(p),XH(u))為用于加權估計的函數, (11) 式中:XP(p)為路段r在時間段p對應的特征向量;XH(u)表示K個最鄰近的歷史特征向量中的一個;d(XP(p),XH(u))表示XP(p)和向量XH(u)按特征向量相似性度量方法求得的向量之間的距離。 本文實驗環境的硬件配置為16 GB內存、1TB的硬盤和一個3.60 GHz 的CPU,操作系統為Windows 7, 64位。實驗中應用Java8進行數據預處理和預測模型的實現,使用MySQL5.1數據庫進行數據的存儲,同時應用Python3.4對實驗的結果進行可視化展示。 本文實驗選取路段按照城市道路劃分標準,選取城市快速路、主干路各一段,并通過百度API計算路段的行車距離,具體的道路信息如表1所示。 表1 選擇的城市道路的詳細信息 為了對模型的預測效果進行評估,需要對預測結果的誤差進行分析。按式(12)計算平均絕對誤差(mean absolute error,MAE)MMAE,按式(13)計算平均相對誤差百分比(mean absolute percentage error,MAPE)MMAPE。 (12) (13) 在KNN算法中,由于K值的選定對于實驗結果影響很大,不同路段、不同時間的最優K選定均不相同。所以本小節首先就K值的標定進行了相關實驗。首先是對于快速路,選定K值在3~80,計算實驗結果的平均相對誤差,得到的結果如圖3所示。可以發現,K在取值20時平均相對誤差的值便收斂趨于穩定,在K取值31時,平均相對誤差的值最小為0.052。 圖3 快速路平均相對誤差隨K值的變化 通過交叉驗證方式計算,對于不同路段的最優K值選定如表2所示。 表2 不同路段的最優K值選定 取K值為31,通過歷史數據對快速路在2016-03-05和2016-03-06的路段行程時間進行預測,預測結果和實際行程時間的對比如圖4、5所示。 圖4 快速路在2016-03-05的行程時間預測 圖5 快速路在2016-03-06的行程時間預測 對快速路行程時間預測的誤差分析表明,2016-03-05預測結果的平均相對誤差值為0.022,2016-03-06預測結果的平均相對誤差值為0.028。結果表明:行程時間預測模型較好地適應了快速路的情況。具體的相對誤差如圖6和圖7所示。 取K值為23,通過歷史數據對主干路在2016-03-05和2016-03-06的路段行程時間進行預測,預測結果和實際行程時間的對比如圖8、9所示。 圖6 快速路在2016-03-05的行程時間預測相對誤差圖 圖7 快速路在2016-03-06的行程時間預測相對誤差圖 圖8 主干路在2016-03-05的行程時間預測 圖9 主干路在2016-03-06的行程時間預測 對主干路行程時間預測的誤差分析表明:2016-03-05預測結果的平均相對誤差值為0.092,2016-03-06預測結果的平均相對誤差值為0.071。通過主干路的行程時間預測可以發現,尤其是在對3月6日的結果預測中,對少數行程時間相對很長的時間段(即嚴重擁堵時段)的預測結果誤差很大,說明預測模型對突發的路段嚴重擁堵情況的適應情況不是很好。 綜合上面的實驗結果,得到預測模型的預測結果誤差如表3所示。 表3 實驗結果誤差 為了對比基于KNN算法的行程時間預測模型的效果,本節將基于KNN算法的預測模型與常用的歷史平均模型以及自回歸移動平均模型(ARIMA模型)的結果進行對比。得到對快速路和主干路的預測結果,如表4、5所示。 表4 不同模型在快速路的預測結果 表5 不同模型在主干路的預測結果 由表4、5的結果容易發現:基于KNN算法的行程時間預測模型在快速路的預測結果要明顯優于歷史平均模型和ARIMA模型的預測結果。 本文基于汽車電子標識數據集,提出了基于KNN算法的城市路段行程時間短時預測方法,結果表明:在城市快速路和主干路都取得了較好的預測效果。本文的預測結果可為大量的城市駕車出行車的道路選擇提供參考信息,以讓出行者避免擁堵而減少通勤時間;另一方面可為城市交通管理者提供相關的決策信息。 在下一步研究中,一方面可考慮實時處理汽車電子標識流數據,提高短時行程時間預測的實時性,同時可增大實驗的數據集,并將歷史數據集按是否擁堵、是否為周末等進行分類,分別對相應的數據集構建預測模型,以進一步提高預測結果的精確性。2 基于KNN的城市路段行程時間預測模型
2.1 K最近鄰算法
2.2 數據準備
2.3 構造特征向量
2.4 K值確定
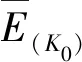
2.5 特征向量相似性度量
2.6 局部估計方法
3 實驗
3.1 實驗環境

3.2 評價指標
3.3 實驗結果與分析





3.4 對比實驗


4 結束語

