CFRP反射器型面主動控制和作動器位置優(yōu)化

伍科，張華振，蘭瀾,周陽

1. 西安空間無線電技術(shù)研究所，西安 710100 2. 上海躍盛信息技術(shù)有限公司，上海 200240

高精度、大空間反射器的研究越來越受到人們的關(guān)注。提高反射面精度的方法是人們對高精度反射器研究的重要方向。國外已有了許多高精度反射器研究的方法和案例。

Pearson等[1]研究了一種大型高精度充氣薄膜反射器的設(shè)計和分析方法。Lang等[2]設(shè)計了一種高精度殼體反射器結(jié)構(gòu)，并提出了一種殼體反射器的結(jié)構(gòu)優(yōu)化和型面調(diào)整方法。Shi等[3]提出了一種對于空間索網(wǎng)反射器網(wǎng)面的幾何生成方法。Yuan等[4]提出了一種可提高大型可展開網(wǎng)格反射器表面精度的設(shè)計方案。Soykasap和Tan[5]設(shè)計并分析了一種高精度采用偏置加筋彈簧支撐的碳纖維增強(qiáng)復(fù)合材料(CFRP)反射器。雖然被動的方法對提高反射面精度做出了很大努力,但主動型面控制方法仍是提高反射面精度的最有效途徑之一。

智能材料和結(jié)構(gòu),諸如聚偏氟乙烯(PVDF)、鋯鈦酸鉛(PZT)、宏觀壓電纖維復(fù)合材料(MFC)、形狀記憶合金(SMA) 作動器/傳感器廣泛應(yīng)用于主動型面/振動控制。Tabata和Natori[6]研究了空間可展開天線的反射器主動型面校正方法以及其可行性。Fang等[7]提出了一種運用PVDF作動器對大型高精度薄膜反射器進(jìn)行自適應(yīng)控制的系統(tǒng)設(shè)計方案。Wang等[8]提出了一種求解壓電作動器控制電壓的方法，并將其用于空間反射器的型面調(diào)整。Stein和Gorinevsky[9]開發(fā)了一種利用大型封裝PZT作動器陣列對反射面進(jìn)行主動形狀控制的技術(shù)。Andoh等[10]提出了一種利用有限個數(shù)的作動器對反射器型面進(jìn)行控制的方法。Lu等[11]采用SMA作動器,來提高圓形薄膜結(jié)構(gòu)的型面精度，建立了薄膜結(jié)構(gòu)的分析模型和求解方法，并利用有限元方法驗證了典型熱載荷下分析模型的有效性。Desmidt等[12]研究了一種主動繩索控制系統(tǒng)及其可行性,并將其應(yīng)用于控制由熱載荷引起的反射器型面的全局誤差。Wu等[13]提出了利用PZT和MFC作動器同時進(jìn)行主動控制，分別用來降低CFRP格柵反射器的全局型面誤差和局部型面誤差。宋祥帥等[14]運用影響系數(shù)矩陣法研究了格柵反射器的作動器電壓配置問題，得到了使型面均方根誤差最小的電壓值和相應(yīng)的均方根(RMS)誤差，但對于作動器數(shù)量的限制和位置的優(yōu)化配置問題并沒有進(jìn)行研究。

大型空間反射器結(jié)構(gòu)由于在發(fā)射過程中受結(jié)構(gòu)重量和體積的限制而無法使用過多數(shù)量的作動器。因此，為了提高反射器結(jié)構(gòu)型面主動控制效率，研究在有限數(shù)量作動器的條件下，作動器位置優(yōu)化分布至關(guān)重要。

目前已經(jīng)有較多的研究針對振動或者型面控制中作動器的幾何尺寸、空間分布位置和加載電壓進(jìn)行了優(yōu)化。但大多數(shù)研究集中于研究梁、板結(jié)構(gòu)的振動和形狀控制。

Suleman和Goncalves[15]優(yōu)化了矩形懸臂組合梁的驅(qū)動器的尺寸和位置,其目標(biāo)是使結(jié)構(gòu)的位移最大、質(zhì)量和電壓最小。Adali等[16]采用一維搜索的優(yōu)化算法來確定層合梁結(jié)構(gòu)的作動器位置。Aldraihem等[17]優(yōu)化了執(zhí)行器的長度和位置,其目標(biāo)函數(shù)是使進(jìn)行加權(quán)后可控性最大。Barboni等[18]通過最優(yōu)性條件的解析解，優(yōu)化了振動控制中簡支梁執(zhí)行器的長度和位置。Bruant等[19]采用基于梯度的優(yōu)化方法對3根梁組合結(jié)構(gòu)中作動器的長度和位置進(jìn)行了優(yōu)化，其目標(biāo)為使機(jī)械能最小以及系統(tǒng)的可觀測性最大。

以上這些方法的共同特點為優(yōu)化迭代的前進(jìn)方向基于目標(biāo)函數(shù)對優(yōu)化變量的梯度。其優(yōu)點為對于凸規(guī)劃問題能夠精確地逼近目標(biāo)函數(shù)的最優(yōu)解。但是，對于復(fù)雜的大型空間結(jié)構(gòu)或大型離散變量的優(yōu)化問題，精確獲取目標(biāo)函數(shù)的梯度十分困難，且基于梯度的優(yōu)化方法容易陷入局部最優(yōu)解。

隨機(jī)搜索算法是研究結(jié)構(gòu)振動或者形狀控制問題中的另一種優(yōu)化方法。Dong和Huang[20]研究了基于多點近似函數(shù)和遺傳算法(GA) 的桁架拓?fù)鋬?yōu)化問題。An等[21]采用兩級多點逼近法研究了自適應(yīng)桁架的作動器分布的優(yōu)化問題。Liu和Lin[22]通過模擬退火算法對于懸臂板的形狀控制問題優(yōu)化了作動器分布和相應(yīng)控制電壓。

隨機(jī)搜索算法的優(yōu)點在于不需要獲得目標(biāo)函數(shù)的梯度,對于復(fù)雜優(yōu)化問題和離散變量的優(yōu)化問題具有明顯的優(yōu)勢。但隨機(jī)搜索算法所得到的最優(yōu)解的精度可能低于基于梯度的方法。

本文研究了基于PZT作動器的CFRP主控格柵反射器的型面控制問題。首先，采用了一種具有獨立電壓自由度的梁單元，以及考慮高階剪切變形的板單元，并運用能量變分哈密爾頓原理推導(dǎo)出了主控格柵反射器的有限元控制方程，根據(jù)推導(dǎo)的有限元控制方程，給出了反射面型面殘余RMS誤差最小的電壓最優(yōu)控制方法。

對于型面控制中的作動器位置優(yōu)化分布問題，基于控制后殘余RMS誤差最小，提出了一種將自適應(yīng)遺傳算法和梯度投影方法相結(jié)合的改進(jìn)優(yōu)化方法，以解決在限定作動器數(shù)量的條件下，作動器幾何位置的優(yōu)化問題。這種方法采用遺傳算法獲得作動器的幾何分布，采用罰函數(shù)法約束作動器的個數(shù)，然后運用梯度投影方法求解約束二次規(guī)劃問題中作動器的電壓。通過數(shù)值算例得到并驗證了提出算法的正確性和有效性。制作了大型主控格柵反射器的實驗樣機(jī)，在高精度光學(xué)平臺上針對CFRP格柵反射器的制造誤差運用PZT作動器進(jìn)行了型面控制實驗。

1 有限元模型

主控CFRP格柵反射器的幾何模型如圖1所示。反射器所使用的CFRP材料鋪層方向為[0°/45°/-45°/90°]s。PZT作動器的總數(shù)為72個，通過預(yù)緊螺母安裝在每一個小格柵的開鑿處。反射器約束的位置為格柵中心交叉處，約束方式為鎖定中心處6個自由度的位移。格柵反射器的設(shè)計幾何尺寸如表1所示。

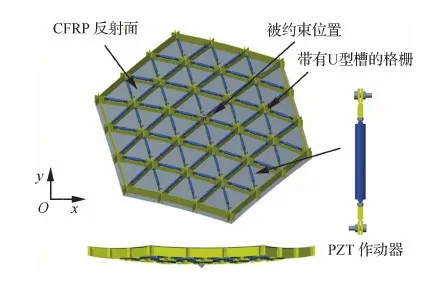
圖1 主控CFRP格柵反射器的幾何模型Fig.1 Geometric schematic of active CFRP rib reflector

表1 主控格柵反射器的結(jié)構(gòu)參數(shù)Table 1 Structural parameters of active rib reflector

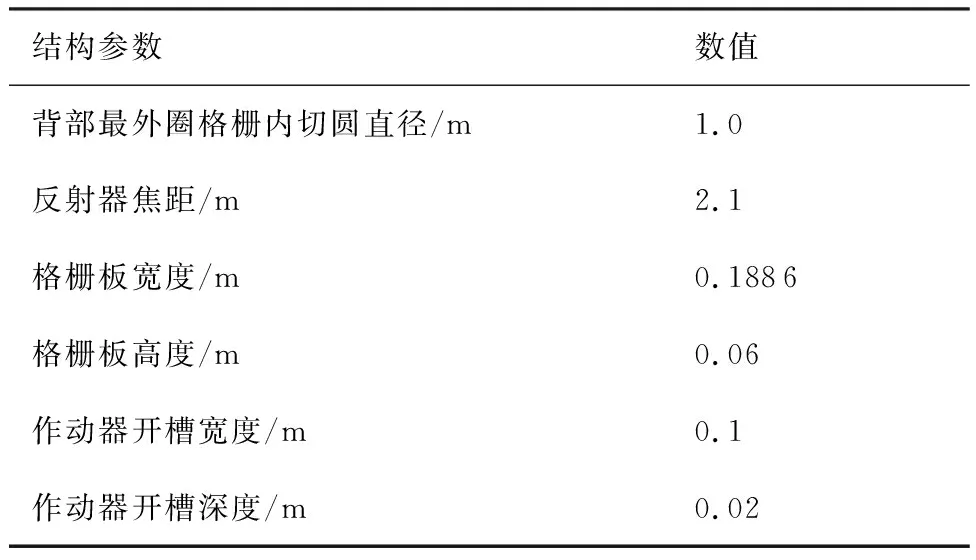
結(jié)構(gòu)參數(shù)數(shù)值背部最外圈格柵內(nèi)切圓直徑/m1.0 反射器焦距/m2.1 格柵板寬度/m0.1886 格柵板高度/m0.06 作動器開槽寬度/m0.1 作動器開槽深度/m0.02

1.1 位移和應(yīng)變假設(shè)

Reddy[23]提出了一種考慮高階剪切形變的層合板單元，它相比普通層合板單元具有更高的計算精度。本文使用這種考慮高階剪切變形的層合板單元來對CFRP層合板進(jìn)行建模。假設(shè)其位移可以寫為

u(x,y,z)=u(x,y,0)+zφy(x,y,0)-

(1)

v(x,y,z)=v(x,y,0)+zφx(x,y,0)-

(2)

w(x,y,z)=w(x,y,0)=w0(x,y)

(3)

式中：u、v、w為板單元沿x、y、z方向的位移；φx和φy分別為在yOz和xOz平面內(nèi)的轉(zhuǎn)角；h為層合板的厚度。坐標(biāo)系為定義在板單元幾何中心處的單元局部坐標(biāo)系，平面z=0為層合板厚度方向中心面所在的平面，層合板的幾何方程為

(4)

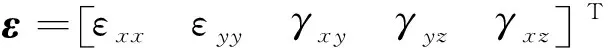
對于PZT作動器，運用三維梁單元對其進(jìn)行建模，假設(shè)其位移可以寫為

u′=u′0(x,0,0)+yφ′z(x,0,0)+zφ′y(x,0,0)

(5)

v′=v′0(x,0,0)

(6)

w′=w′0(x,0,0)

(7)

式中:u′、v′和w′為PZT梁單元沿x、y以及z方向的位移；φ′y和φ′z分別為在xOz和xOy平面內(nèi)的轉(zhuǎn)角。其坐標(biāo)系為位移梁單元節(jié)點處的單元局部坐標(biāo)系。三維梁單元的幾何方程可以表示為

(8)

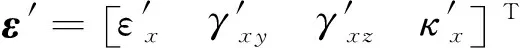
1.2 本構(gòu)方程

正交各向異性板單元的本構(gòu)方程為[23]

(9)

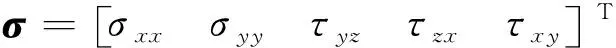
(10)

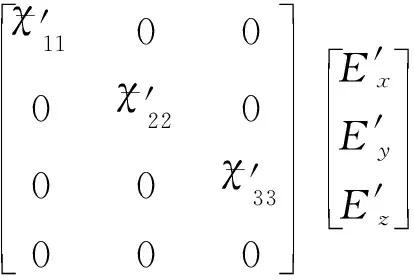
(11)

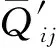
1.3 插值形式

使用4節(jié)點的二維板單元對碳纖維層合板進(jìn)行建模，板單元的每個節(jié)點具有7個自由度。運用Hermite插值函數(shù)[24]對單元內(nèi)部區(qū)域進(jìn)行插值。對于板單元,其單元位移向量可以表示為

(12)

單元的節(jié)點位移向量de可表示為

(13)

i=1,2,3,4

(14)

式(12)～式(14)中:N為3×28的運用Hermite函數(shù)進(jìn)行插值的板單元型函數(shù)矩陣，其具體形式見附錄;節(jié)點位移向量de為28×1的行向量。將式(12)代入式(4)，板單元的應(yīng)變向量可表示為

(15)

式中:B為板單元的應(yīng)變矩陣。

對于PZT壓電梁單元，其位移插值形式可以表示為

(16)

應(yīng)變向量可以表示為

(17)

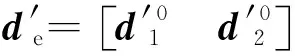
(18)

梁單元的型函數(shù)N′的形式見附錄A[25]。

1.4 變分形式

運用廣義Hamilton變分原理來推導(dǎo)主控系統(tǒng)的平衡方程。廣義Hamilton變分等式可以表示為

(19)

式中:K為系統(tǒng)的動能;P為系統(tǒng)的勢能;W為外力功;t1和t2分別為起始和終止時間。對于靜力學(xué)分析，K=0。對于本文研究的主控格柵反射器，其勢能包括彈性勢能和電勢能，其一般形式為

(20)

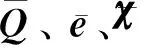
對于PZT壓電梁單元，其電場可表示為

(21)

式中:U′e為壓電梁單元的加載電壓;l為作動器的長度;L為線性算子。將式(16)和式(21)代入式(20)，壓電梁單元的總勢能進(jìn)一步可表示為

(22)

(23)

(24)

(25)

式中:K′m、K′me和K′ee分別為力學(xué)剛度矩陣、機(jī)電耦合矩陣以及電勢矩陣。

對于CFRP層合板單元，壓電常數(shù)矩陣和介電常數(shù)矩陣均為零矩陣，單元的勢能可以表示為

(26)

式中:Km為CFRP層合板單元的單元剛度矩陣。系統(tǒng)的外力功可以表示為

(27)

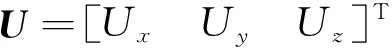
(28)

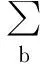
將每個單元中局部坐標(biāo)系通過乘以相應(yīng)的雅可比矩陣轉(zhuǎn)換為整體坐標(biāo)系，在整體坐標(biāo)系下，對單元節(jié)點平衡方程進(jìn)行組裝可以得到在整體坐標(biāo)系下所有節(jié)點平衡方程的矩陣形式。由于變分量的任意性，變分方程式(28)可以轉(zhuǎn)化為整體坐標(biāo)系下的代數(shù)方程：

(29)

式中：d為全局坐標(biāo)系下的單元節(jié)點位移向量；Km、Kme和Kee分別為全局坐標(biāo)下總力學(xué)剛度矩陣、總機(jī)電耦合矩陣以及總電勢矩陣；U為所有壓電單元的電壓向量；F為節(jié)點的外力向量；Q為作用在壓電單元上的外電荷。通過解式(29)，可以得到系統(tǒng)的節(jié)點位移和作動器的電壓。

2 最優(yōu)控制器設(shè)計

對于研究的主控格柵反射器，本節(jié)基于所建立的有限元模型，設(shè)計了反射器型面控制的最優(yōu)控制器。對于反射器在空間環(huán)境下所承受的任意力和位移載荷，當(dāng)作動器數(shù)量給定時，均能給出當(dāng)前數(shù)量作動器的最優(yōu)位置分布以及相應(yīng)的加載電壓，使得控制后殘余RMS誤差最小。

2.1 型面最優(yōu)控制數(shù)學(xué)模型

反射面的幾何示意圖如圖2所示，整體坐標(biāo)系的原點位于拋物面反射器的頂點。y坐標(biāo)軸通過拋物面的焦點，反射面上節(jié)點的RMS誤差被定義為

(30)

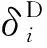
PZT作動器的安裝位置為反射器小三角格柵的開鑿處，預(yù)留的待選位置總共有72個，考慮到作動器的重量，實際使用的作動器個數(shù)應(yīng)少于72。在優(yōu)化模型中，為了表示一定數(shù)量的作動器的分布情況，用一個72位的二進(jìn)制0，1編碼的向量代表該處有沒有作動器，1代表該處裝有作動器，0代表該處無作動器。因此，根據(jù)所建立的主控反射器系統(tǒng)的有限元模型(式(29))，主控反射器型面最優(yōu)控制的數(shù)學(xué)模型可以寫為

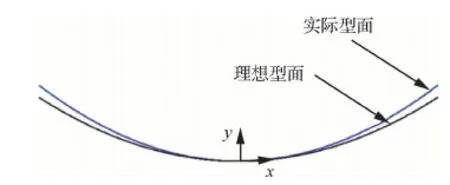
圖2 反射器的實際型面和理想型面Fig.2 Actual and desired shapes of reflector

(31)

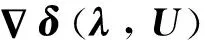
2.2 求解方法

改進(jìn)的優(yōu)化方法的具體步驟為

步驟1 由遺傳算法隨機(jī)生成一定數(shù)量的二進(jìn)制向量λ個體作為初始種群，表示作動器分布。

步驟2 對于種群每一個個體，λ為已知二進(jìn)制向量，交由梯度投影方法求出每一個個體的加載電壓以及相應(yīng)的殘余RMS誤差，將殘余RMS誤差作為個體的適應(yīng)度。

步驟3 保留最優(yōu)個體，直接到下一代中，不參與交叉和變異。

步驟4 根據(jù)個體適應(yīng)度，通過輪盤賭進(jìn)行選擇，將所選個體運用自適應(yīng)交叉和變異算子進(jìn)行篩選并重新插入種群中。

步驟5 更新每一個個體的二進(jìn)制編碼λ，返回步驟2進(jìn)行迭代，直至種群最優(yōu)個體適應(yīng)度變化小于設(shè)定值或達(dá)到最大迭代次數(shù)。

步驟6 輸出迭代結(jié)束時，種群中的最優(yōu)個體對應(yīng)的二進(jìn)制編碼λ，代表作動器的位置分布；相應(yīng)的電壓向量U和相應(yīng)的殘余RMS誤差值。

對于步驟2中，當(dāng)λ確定時，相應(yīng)電壓后殘余RMS誤差的求解方法為：假設(shè)系統(tǒng)的節(jié)點總位移個數(shù)為p，反射面上節(jié)點在y方向的位移個數(shù)為q，總電壓自由度個數(shù)為r。將式(31)中目標(biāo)函數(shù)f寫為

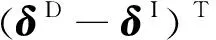
(32)

(33)

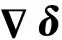
(34)

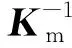
Ks(F-KmeU)(δD-δI)+

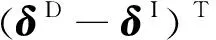
(35)

式(35)可以進(jìn)一步簡化為

f(U)=UTAU-bTU+c

(36)

式中:

(37)

(38)

(39)

A為r×r維的正定方陣;b為r維的列向量;c為常數(shù)。同樣，優(yōu)化模型中第3個約束不等式也可以寫成矩陣形式。因此，優(yōu)化模型式(31)可以轉(zhuǎn)化為如下有邊界約束的二次規(guī)劃的形式：

(40)

優(yōu)化模型式(40)可以通過約束二次規(guī)劃問題中梯度投影法(GPM)進(jìn)行求解。

將求得的目標(biāo)函數(shù)即RMS誤差作為對應(yīng)個體的適應(yīng)度，繼續(xù)進(jìn)行步驟3中的選擇、交叉和變異，當(dāng)?shù)瓿蓵r，即可求出相應(yīng)載荷下，一定數(shù)量作動器的最優(yōu)位置分布、相應(yīng)電壓以及殘余RMS誤差。特別地,為了防止在步驟4中，種群中個體在交叉和變異過程中，代表作動器位置的編碼向量λ中作動器個數(shù)超出限定個數(shù)，采用罰函數(shù)對作動器超出規(guī)定個數(shù)的個體對應(yīng)的目標(biāo)函數(shù)進(jìn)行懲罰。作動器數(shù)量超出的個數(shù)越多，罰函數(shù)懲罰的力度越大。動態(tài)罰函數(shù)的表達(dá)式為[26]

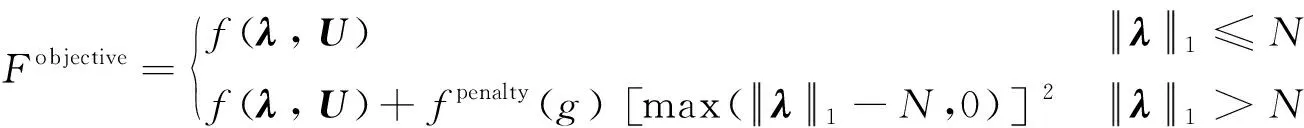
(41)

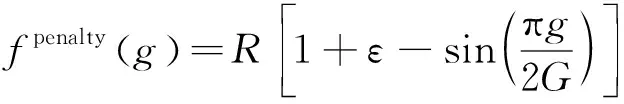
(42)

式中：fpenalty(g)為隨種群迭代次數(shù)變化的動態(tài)懲罰因子;R為反函數(shù)比例系數(shù);ε為正的參數(shù);g和G分別為當(dāng)前的迭代次數(shù)和總共的迭代次數(shù)。在迭代過程中，產(chǎn)生的新個體作動器數(shù)量超過規(guī)定數(shù)量越多，懲罰的力度越大；并且開始迭代時采用較大的處罰因子，隨著迭代次數(shù)的增加，逐漸減小，用以提高種群的迭代效率，加速收斂的過程。遺傳算法中的交叉、變異算子采用自適應(yīng)交叉和變異。自適應(yīng)交叉和變異算子的表達(dá)式為

(43)

(44)

式中:Pc1、Pc2為最小以及最大的交叉概率;Pm1、Pm2為最小以及最大的變異概率；f′為種群中個體的適應(yīng)度；f′max為種群每代個體迭代最大適應(yīng)度;f′ave為種群每代的平均適應(yīng)度。

圖3為對作動器位置進(jìn)行優(yōu)化運用的優(yōu)化算法流程圖。首先隨機(jī)生成72個代表作動器位置的隨機(jī)二進(jìn)制串，作為優(yōu)化變量；根據(jù)每一個二進(jìn)制變量代表的作動器位置分別建立有限元模型；然后，運用上述方法將型面最優(yōu)問題轉(zhuǎn)化為式(40) 所述的二次規(guī)劃問題，求出相應(yīng)作動器分布情況下對應(yīng)的電壓和殘余RMS誤差，并將RMS誤差作為其種群中個體的目標(biāo)函數(shù)值；根據(jù)每一串二進(jìn)制變量代表的作動器個數(shù)是否超出準(zhǔn)許范圍，運用式(41)和式(42)進(jìn)行懲罰，從而得到種群中每一個個體的適應(yīng)度；根據(jù)個體的適應(yīng)度進(jìn)行選擇、交叉和變異操作，從而進(jìn)化出新的種群，重新進(jìn)行迭代。保留每一代種群中的最優(yōu)個體，直到滿足結(jié)束迭代的條件，將最優(yōu)個體二進(jìn)制變量作為作動器分布方式，并求出相應(yīng)的作動器電壓。

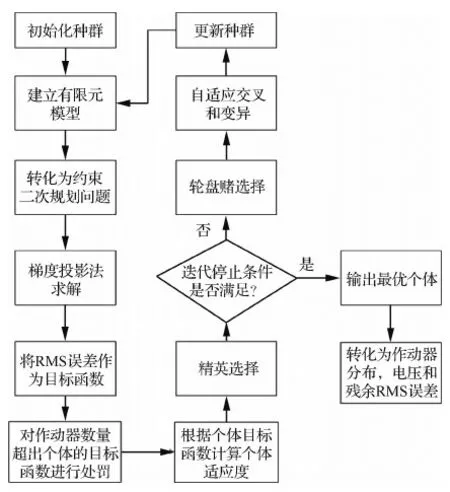
圖3 作動器分布位置優(yōu)化流程Fig.3 Flow chart of actuator placement optimization

2.3 數(shù)值算例

式(29)中剛度矩陣可借助于有限元軟件ANSYS 14.0進(jìn)行建立并提取。優(yōu)化以及控制算法采用MATLAB 2013b進(jìn)行編制，迭代的過程在MATLAB中進(jìn)行，完成時給出相應(yīng)的作動器分布、配置電壓以及殘余RMS誤差。以下給出了兩組算例。反射器的約束位置為如圖1所示的節(jié)點處，其6個自由度被約束。

1) 反射器受整體彎矩作用

施力方式為反射器邊緣對稱角點處等大反向的10 N垂向作用力，作用點距離為1.1 m，產(chǎn)生的整體彎矩為11 N·m。反射面的初始RMS值為266.5 μm，其位移誤差云圖如圖4所示。

運用本文提出的優(yōu)化方法，對此工況下作動器的位置分布以及相應(yīng)電壓進(jìn)行優(yōu)化。假設(shè)N=14,即作動器數(shù)量限制為14個。遺傳算法的迭代曲線如圖5所示。圖6為優(yōu)化后的作動器位置和相應(yīng)電壓大小。

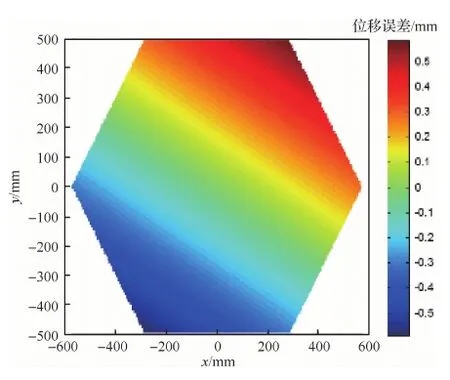
圖4 反射面受彎矩作用位移誤差云圖Fig.4 Contour of displacement error of reflector surface under a bending moment

由迭代曲線圖5可以看出，所提出混合優(yōu)化算法收斂速度很快，80次迭代以后目標(biāo)值保持不變。控制后的殘余RMS誤差為44.1 μm。

2) 反射面上節(jié)點位移取Zernike多項式線性組合的形式

取六邊形域內(nèi)前5階正交Zernike多項式組成的線性組合，作為反射面型面節(jié)點的位移誤差，其表達(dá)式為[27]

(45)

式中:Sd(ρ、θ)為反射面上坐標(biāo)為(ρ、θ)點的位移；Zi(ρ、θ)為第i階Zernike多項式。將反射面上節(jié)點的坐標(biāo)代入式(45)，可以得到反射面上所有節(jié)點的位移誤差云圖，如圖7所示。運用改進(jìn)優(yōu)化算法對其進(jìn)行優(yōu)化，作動器數(shù)量的限制分別設(shè)為10、20以及35。圖8為3種作動器數(shù)量限制時遺傳算法的迭代曲線。當(dāng)作動器數(shù)量限制為10個時，殘余RMS誤差為7.25 μm；當(dāng)作動器數(shù)量限制為20個時，殘余RMS誤差為5.1 μm；當(dāng)作動器數(shù)量限制為35個時，殘余RMS誤差為4.9 μm。相應(yīng)的作動器位置分布情況、電壓大小以及殘余型面誤差云圖如圖9所示。在當(dāng)前型面誤差情況下，當(dāng)作動器數(shù)量限制從4個一直到72個變化時，將每次優(yōu)化的最終RMS誤差用曲線連接，如圖10所示。從圖10可以看出，隨著作動器數(shù)量增加，殘余誤差逐漸減小，當(dāng)作動器數(shù)量達(dá)到臨界點(40個)時，控制誤差到達(dá)最小飽和值。

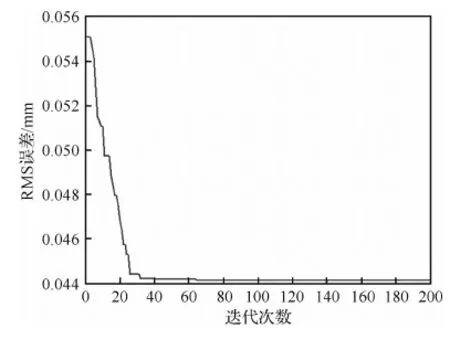
圖5 優(yōu)化迭代曲線(14個作動器)Fig.5 Iteration curve of optimization (14 actuators)

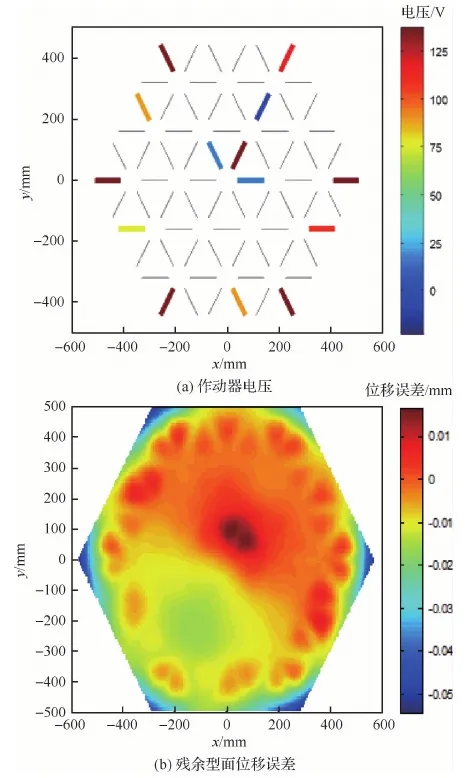
圖6 作動器電壓以及殘余型面位移誤差Fig.6 Voltages of actuators and residual surface displacement error

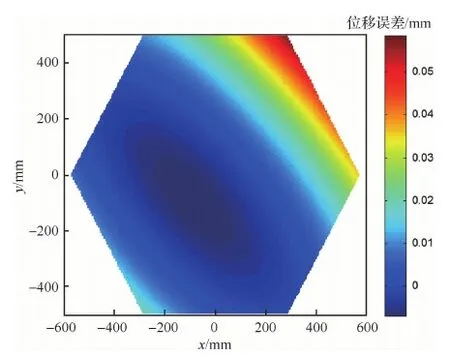
圖7 Zernike多項式線性組合的位移誤差云圖Fig.7 Contour of displacement error of linear combination of Zernike polynomials

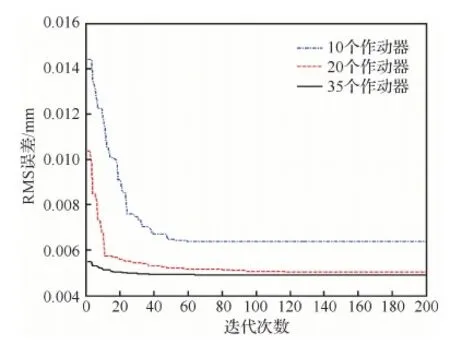
圖8 作動器數(shù)量分別為10、20和35時的迭代曲線Fig.8 Iteration curves with 10, 20, and 35 actuators

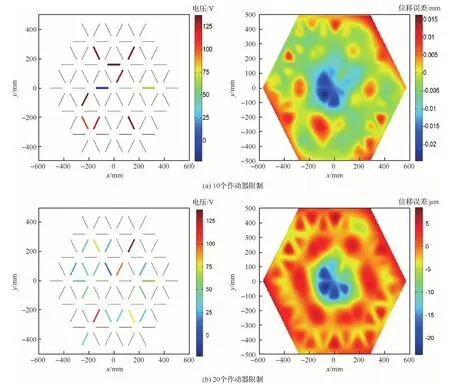
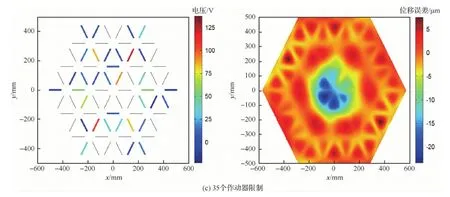
圖9 3種情況下作動器電壓以及相應(yīng)殘余誤差云圖Fig.9 Voltages of actuators and corresponding residual surface errors contours in three cases

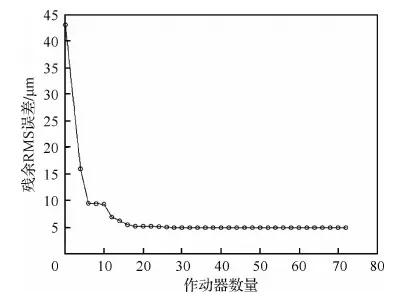
圖10 殘余RMS誤差隨作動器數(shù)量的變化Fig.10 Variation of residual RMS error with number of actuators

3 樣機(jī)制作與實驗驗證

制作了CFRP復(fù)合材料格柵反射器，外沿直徑為1.2 m，有效區(qū)域為內(nèi)切圓直徑1.0 m的正六邊形區(qū)域，焦距為2.1 m。格柵反射器的型面主動控制實驗系統(tǒng)在恒溫恒濕實驗室中的高精度光學(xué)平臺上搭建并完成。實驗環(huán)境以及主控高精度格柵反射器樣機(jī)照片如圖11所示。每節(jié)格柵上安裝一個PZT作動器以實現(xiàn)反射器的型面控制，PZT作動器的總數(shù)為72支。反射器背部格柵中心處用夾具進(jìn)行固定并將夾具底座完全固定于光學(xué)平臺上。圖12為作動器電壓控制器軟件和硬件設(shè)施。

反射面上靶點的位移采用V-STARS攝影測量儀進(jìn)行測量，作為輸入電壓的反饋。V-STARS攝影測量系統(tǒng)組件如圖13所示。它是一種利用光學(xué)三角定位法進(jìn)行標(biāo)定的高精度攝影測量工具。主控反射器系統(tǒng)實驗測量現(xiàn)場如圖14所示。

測量靶點共469個，位于反射面上均勻分布。對測量得到的靶點坐標(biāo)進(jìn)行定焦擬合，可得到固定焦距下反射面的型面誤差。

圖11 實驗環(huán)境和主控格柵反射器樣機(jī)Fig.11 Experimental environment and prototype of active rib reflector

圖12 電壓控制系統(tǒng)軟、硬件Fig.12 Hardware and software of voltage control system

圖13 V-STARS攝影測量系統(tǒng)組件Fig.13 Components of V-STARS photogrammetry system

圖14 主動型面控制實驗測量系統(tǒng)Fig.14 Experiment measurement system for active shape control

3.1 單個PZT作動器線性度驗證

首先對PZT作動器給定電壓輸入時，反射面產(chǎn)生位移的線性度進(jìn)行驗證，確保分析和實驗基本假設(shè)的正確性。對反射器上某一內(nèi)圈作動器分別加載25、50、75、100、150 V電壓，并測量反射面上節(jié)點相應(yīng)的位移。5個靶點分別位于圖14中反射器邊緣的沿雙向箭頭方向上，標(biāo)號分別為 1～5。圖15為反射面上5個節(jié)點在不同電壓下的位移曲線，從圖可以看出，反射面上節(jié)點的位移和電壓呈近線性關(guān)系，從而從實驗上驗證了主動控制反射器結(jié)構(gòu)的力學(xué)模型符合線性本構(gòu)關(guān)系的假設(shè)。

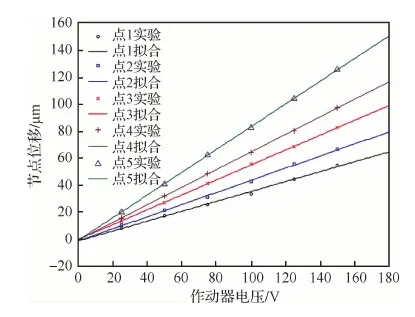
圖15 反射面上5個點的位移Fig.15 Displacement of 5 points on reflector surface

3.2 有限元模型的實驗驗證

由于主控格柵反射器型面最優(yōu)控制器的設(shè)計建立在有限元模型的基礎(chǔ)之上，因此建立的有限元分析模型與真實物理系統(tǒng)的一致性將關(guān)系到型面控制實驗的效果。將分析模型中每個PZT作動器加載50 V電壓計算得到的反射面型面變形與真實樣機(jī)的測試結(jié)果進(jìn)行對比，圖16為其中3個作動器加載50 V電壓時型面變形誤差云圖的計算和實驗結(jié)果。從圖16可以看出，作動器在50 V 電壓下產(chǎn)生的反射面形變云圖計算結(jié)果和實驗結(jié)果很接近。因此，證明了所建立的有限元模型的正確性，為進(jìn)一步實現(xiàn)反射面的型面控制確立了基礎(chǔ)。

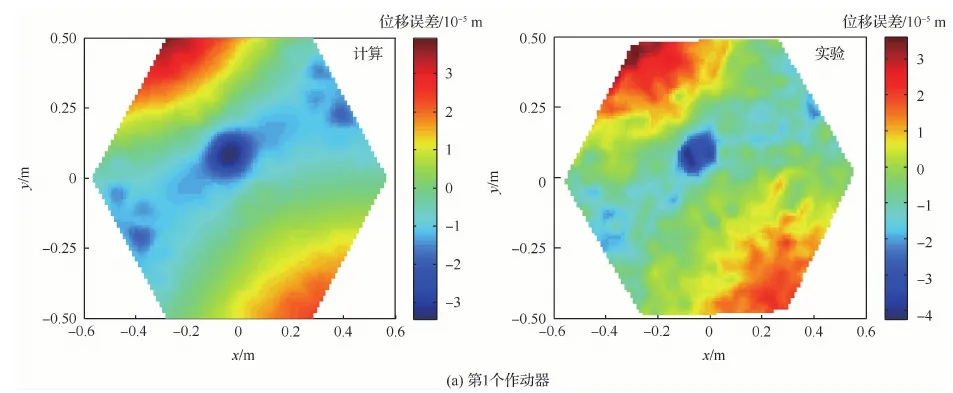
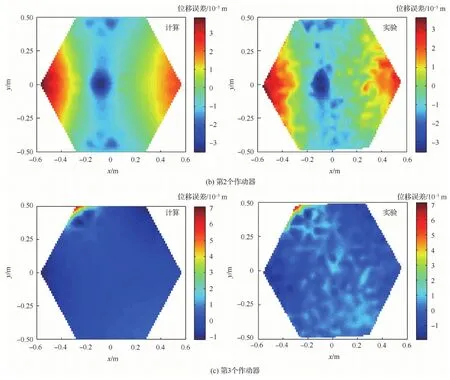
圖16 反射面在不同作動器作用下位移誤差云圖Fig.16 Displacement error contours of reflector surface with different implementations of actuators

3.3 反射面初始制造誤差的型面控制

CFRP復(fù)合材料格柵反射器的初始型面精度受到模具精度、固化成型中產(chǎn)生的應(yīng)力的影響，因此，反射器的型面會存在一定的初始型面誤差。本實驗針對格柵反射器的初始型面誤差，采用PZT壓電作動器進(jìn)行型面的主動調(diào)整。反射器的初始型面誤差云圖如圖17所示。

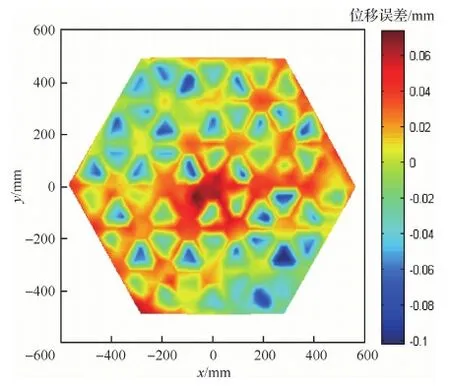
圖17 反射器的初始型面誤差Fig.17 Initial surface error of reflector

反射面的初始RMS誤差為43.4 μm。運用72支PZT壓電作動器對型面進(jìn)行主動控制，控制后殘余誤差的分布云圖計算分析與實驗的結(jié)果如圖18所示。從圖18可以看出，控制后型面的殘余誤差云圖，分析結(jié)果與實驗結(jié)果比較接近。分析的殘余RMS誤差為17.8 μm。實驗測量的殘余RMS誤差為19.5 μm，與計算結(jié)果較為接近，型面控制的效果顯著。72支作動器相應(yīng)的電壓分布如圖19所示。

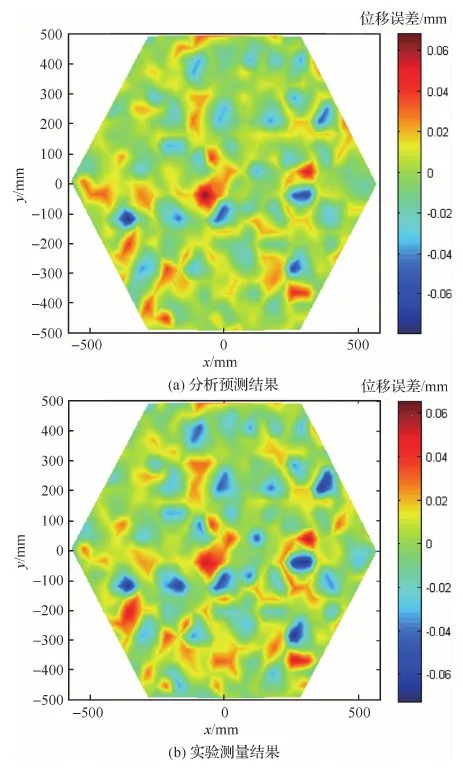
圖18 控制后反射器型面的殘余誤差Fig.18 Residual error of reflector surface after control

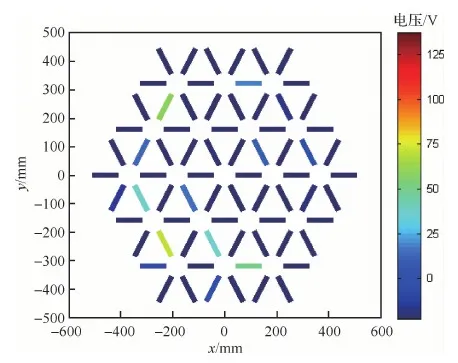
圖19 主動型面控制的電壓分布Fig.19 Distribution of voltages of active shape control

4 結(jié) 論

本文研究了CFRP格柵反射器的型面主動控制問題。從理論上建立了主控格柵反射器的有限元模型，基于建立的有限元模型提出了一種型面控制器的設(shè)計方法，并對PZT作動器的位置分布進(jìn)行了優(yōu)化。最后，搭建了相應(yīng)的實驗系統(tǒng)。進(jìn)行了主控實驗研究。本文的主要創(chuàng)新點可總結(jié)如下：

1) 設(shè)計了一種關(guān)于CFRP格柵反射器型面控制的方案，運用Hamilton變分原理推導(dǎo)了具有電壓獨立自由度、考慮高階剪切形變的反射器有限元模型。

2) 基于平衡方程推導(dǎo)了型面最優(yōu)控制器的表達(dá)式，反射器的型面控制問題轉(zhuǎn)化為約束二次規(guī)劃問題。

3) 對任意形式的載荷，將自適應(yīng)遺傳算法和梯度投影方法相結(jié)合，求解了限制作動器數(shù)量情況下的作動器位置分布和相應(yīng)電壓的問題。

4) 搭建了主控格柵反射器的實驗系統(tǒng)。針對有限元模型的準(zhǔn)確性以及對制造誤差的控制效果進(jìn)行了實驗驗證。

附錄A

1) 板單元

板單元的形函數(shù)表達(dá)式為

(A1)

i=1,2,3,4

(A2)

2) 梁單元

梁單元的形函數(shù)矩陣可表示為

N′=[K′iK′j]

(A3)

子矩陣K′i和K′j可表示為

(A4)

式中:ξ′為梁單元的形函數(shù)參數(shù)；z′和y′為梁單元局部坐標(biāo)系下的坐標(biāo)；l為梁單元的長度。