改進克里金插值算法的井下無線定位指紋庫構建方法*

劉 夏,莫樹培

(1.貴州工業職業技術學院電子與信息工程學院,貴陽 550000;2.中南大學信息科學與工程學院,長沙 410000)

為提高煤礦安全生產保障能力,國家強制要求全國煤礦都必須建立和完善安全避險六大系統,其系統包括監測監控、人員定位、供水施救、壓風自救、通信聯絡、緊急避險等。煤礦井下人員定位系統能夠及時、準確的將井下各個區域人員的動態情況,使管理人員能夠隨時掌握井下人員運動軌跡。當事故發生時,救援人員可根據井下人員定位系統所提供的數據,迅速獲取有關人員的位置情況,提高應急救援工作的效率。目前井下人員定位系統[1]主要采用RFID區域位置監測技術,只能將井下工作人員定位到一個區域,定位精度不高,無法滿足煤礦智能化對人員或設備定位的需求。

為解決煤礦井下人員定位技術難題,學者們研究用慣性導航、UWB、ZigBee和WIFI等技術進行井下人員定位,其中慣性導航[2]需要移動終端設備增加陀螺儀、加速度計和磁力計等傳感器才能進行定位;UWB技術[3]通信距離在10 m左右,不適合將長距離定位;ZigBee技術[4]傳輸效率慢,對信道帶寬要求較高,從而影響定位效果;WIFI技術[5]因帶寬高、傳輸速度快、價格便宜、部署方便等特點,近年來已經成為研究熱點。WIFI定位技術通過獲取無線信號的相關信息估算出目標位置數據,目前主要有DV-Hop定位[6]、到達時間定位、質心定位和指紋定位等方法,其中到達時間定位[7]需要精確測量信號的傳播時間,對無線設備硬件要求高;質心定位[8]必須已知3個以上無線網絡傳感器或AP節點信息才能實現定位;指紋定位[9]一般分為離線采集階段和在線匹配階段,其關鍵點在于離線采集階段建立采集點密集分布的定位指紋庫[10],傳統方法是逐點采集信號,會耗費大量的人力和時間。針對此問題,郭紅成等[11]提出線性插值法構建指紋庫,存在基點處不光滑,插值精度低;LI等[12]提出反距離加權插值法構建指紋庫,未考慮數據在空間分布情況,會造成觀測點權值不對應而造成估計結果產生偏差;王永星等[13]提出克里金插值算法構建指紋庫,采用克里金插值算法進行估算預測點,但隨著距離h不斷增大,空間相關性不斷減弱,變異性不斷增強,從而會使樣本反映的統計特性偏離實際,導致插值準確度降低。

本文在上述方法基礎上,提出利用模擬退火人工蜂群混合優化算法對克里金插值算法中理論變異函數尋找全局最優解,再利用少量觀測點的信號數據,通過改進克里金插值算法估算出預測點的插值數據,構建完整井下指紋數據庫。實驗結果表明,該構建方法進一步提高定位系統的穩定性和定位精度,而人工采集指紋數據的工作量可減少50%。

1 普通克里金插值算法

克里金插值算法[14]是法國統計學家喬治斯·馬瑟倫(Georges Matheron)于1963年提出,其定義為對已知樣本加權平均,估計平面上的未知點,并使得估計值與真實值的數學期望相同且方差最小的地質統計學過程。

克里金插值算法也稱空間局部插值,其建立在變異函數理論和結構分析的基礎上,能夠對區域變量進行線性無偏最優估計。該算法已經廣泛應用在地質學、環境科學、大氣科學等領域。

設預測點RSSI數據的估計值為z*(x0),第i個位置觀測值為z(x)i,其公式可表示為:

式中λi為第i位置觀測值的權重,m為用于估計待預測點的數量。

區域化變量是指在區域內所在位置有關的隨機變量,在本文中是指在區域內不同位置上的信號強度信息RSSI。設在空間中兩個不同的點x和x+h處的特征值z(x)和z(x)+h存在一定相關性,相關度與兩點間的距離h有關。

變異函數能夠反應區域化變量的空間結構特征,其計算公式可表示為

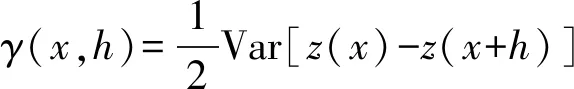
(2)

在區域內滿足二階平穩假設條件下,對任意兩點間的距離h,有E[z(x)]=E[z(x)+h],則變異函數可表示為:

如果γ(x,h)僅依賴于變量h,而于具體的位置x無關,再根據實驗中已測得信號強度信息數據估計出變異函數稱為實驗變異函數,可表示為:

式中M(h)為距離h時的點對數目。

在實驗中采集到樣本有限,對于實驗變異函數γ′(h)在整個區間上隨距離h變化需要通過理論模型來擬合。

理論模型有純塊金效應模型、球狀模型、指數模型和高斯模型等模型,而利用定位區域中無線信息強度求解實驗變異函數是最接近球狀模型的變異函數。球狀模型公式,可表示為:

式中C0為塊金常數,C為供高,C0+C為基臺值,a為變程。

由式(1)可知,要求出z*(x0)的信號強度就必須權值λi的值,λi的值是通過實驗變異函數在無偏性和最小方差條件下,計算得到;由此可以推到出普通克里金方程組為:

(6)

式中μ為Lagrange函數因子。

由式(1)中λi可以通過方程組形式表示為:

式中,γ(xi-xj)的值可以通過球狀模型的變異函數來獲得。式(7)方程組能夠簡寫為:

AW=Z

(8)

式中A,W和Z相應表示式(7)中左、中右矩陣。

權值向量W能夠通過式(8)計算得出:

W=A-1Z

(9)

求解矩陣方程式(9)得到權值λi,待入式(1)可計算出z*(x0),即預測點RSSI的無偏估計插值。

用插值算法可以減少人工采集量指紋的工作量,考慮到井下無線信號強度的空間相關性,克里金插值算法通過整體空間球狀模型變異理論對預測點的作用,當距離h較小時計算出的插值準確度較高;但隨著距離h不斷增大,空間相關性不斷減弱,變異性不斷增強,從而會使樣本反映的統計特性偏離實際,導致插值準確度降低。為此本文提出利用模擬退火人工蜂群混合優化算法對理論變異函數球狀模型參數進行優化,使之能達到全局最優,從而提高插值準確度。

2 模擬退火人工蜂群混合優化算法

人工蜂群算法是模仿蜜蜂行為提出的一種優化方法,可解決多變量函數優化問題,但易陷進局部最小值,且易出現適應值更新停滯現象。為此本文提出利用模擬退火算法來改善人工蜂群算法,結合二種算法優勢,使理論變異函數球狀模型參數能尋到全局最優的解。

2.1 人工蜂群算法

人工蜂群[15-16]ABC(Artificial Bee Colony)算法是由蜂群采蜜行為啟發的算法,通過蜂個體的局部尋優行為,最終在群體中突現全局最優的值。算法中蜂群主要由引領蜂、偵察蜂和跟隨蜂組成,其中引領蜂和跟隨蜂各占整個峰群數量的一半,引領蜂與蜜源兩者之間一一對應,且兩者數量相等。每個蜜源的位置代表優化問題的一個解,蜜源的蜜量對應著算法適應度,適應度值的大小反映蜜源質量,也就是優化問題解的質量,而尋找蜜源任務是由引領蜂和偵察蜂來完成。

人工蜂群算法初期是由引領蜂隨機選擇蜜源位置,并儲存蜜源位置信息,然后根據式(10)在領域內搜索新的蜜源位置,并獲取該蜜源信息。其中式(10)可表示為:

υij=xij+φij(xij-xkj)

(10)

式中υij為新蜜源位置;xij為原來蜜源位置;φij為隨機數,其范圍為[-1,1];j為第j個待優化問題參數維度,j={1,2,…,D},其中D為總維度數;k為隨機選擇的蜜源標號且k≠i。

當所有引領蜂搜索完蜜源后,會用搖擺舞方式將蜜源信息傳遞給跟隨蜂,跟隨蜂根據獲得的蜜源信息選擇蜜源,蜜源量越大被選中的概率也就越大。其概率Pi可表示為:

(11)

式中fiti表示蜜源i的適應度值,N為蜜源的數量。

當某一蜜源未更新的次數達到limit后,舍棄該蜜源,蜜源對應的引領蜂變為偵察蜂,并隨機產生一個新的蜜源位置Sij,產生的公式可表示為:

因為本文需要對克里金插值的理論變異函數進行優化,所以采用的適應度函數[17]為

式中γ′(h)為實驗變異函數,γ(h)為理論變異函數,M為分離距離個數,hm為第m個分離距離。

2.2 模擬退火算法

模擬退火[18]SA(Simulated Annealing)算法是模擬固體退火過程,利用高溫時粒子的無序性,有效地跳出局部最優的陷阱。

將模擬退火算法與人工蜂群算法進行融合,當新蜜源適應度值低于當前蜜源時,按照一定的概率接受新蜜源,從而跳出局部最優的陷阱。其概率PSA可表示為:

式中f(mot)為當前蜜源的適應度值,f′(dau)為新蜜源的適應度值,Tk為當前溫度。

設溫度下降函數為:

Tk=βTk-1

(15)

式中β為降溫系數,β∈[0.75,0.99]。

2.3 模擬退火人工蜂群混合優化算法

根據上述算法公式的建立,模擬退火人工蜂群混合優化[19](SA-ABC)算法實施步驟如下:

步驟1初始化人工蜂群和模擬退火的參數,如蜂群總數SN,蜜源的數量N,蜜源未更新次數limit,初始溫度T0,終止溫度Tmin,退火系數β,最大迭代數Kmax,迭代數k,收斂精度ε等,并把需要優化參數映射到蜜源;

步驟2引領蜂隨機選擇一個蜜源,按式(13)計算當前蜜源的適應度值;

步驟3進入引領蜂階段,引領蜂按式(10)在領域內搜索新蜜源位置,并按式(13)計算新蜜源的適應度值。按照模擬退火機制選擇是否接受新蜜源:若新蜜源更優即f(mot)?時接受新蜜源,否則保留當前蜜源。

步驟4進入跟隨蜂階段,引領蜂用搖擺舞方式將蜜源信息傳遞給跟隨蜂,然后跟隨蜂按式(11)選擇蜜源,并在蜜源領域附近進行搜索新蜜源,并按式(13)計算兩個蜜源的適應度值,按照模擬退火機制選擇是否接受新蜜源。

步驟5當某個蜜源未更新的次數超過limit,則舍棄該蜜源,蜜源對應的引領蜂變為偵察蜂,并按式(12)產生一個新的蜜源,并按式(13)計算該蜜源的適應度值。

步驟6記錄本次迭代的最優解,模擬退火算法按式(15)進行降溫。

步驟7檢查是最優蜜源適應度是否滿足精度要求或迭代次數達到最大迭代次數或當前溫度達到終止溫度,若滿足條件則算法結束,輸出最優的解;否則k=k+1,跳轉到步驟2。

3 SA-ABC-Kriging插值算法流程

模擬退火人工蜂群混合算法優化克里金SA-ABC-Kriging(Simulated Annealing and Artificial Bee Colony optimization Kriging)插值算法流程為:首先由井下采集少量指紋組成采集指紋庫,將該指紋庫信息數據結合Kriging插值構建算法模型;其次對插值算法中的變異函數進行初步擬合,把理論變異函數球狀模型參數映射到模擬退火算法與人工蜂群算法中;再次由模擬退火算法與人工蜂群算法尋優,輸出全局最優的參數;最后完成建立SA-ABC-Kriging插值算法模型,具體流程如圖1所示。

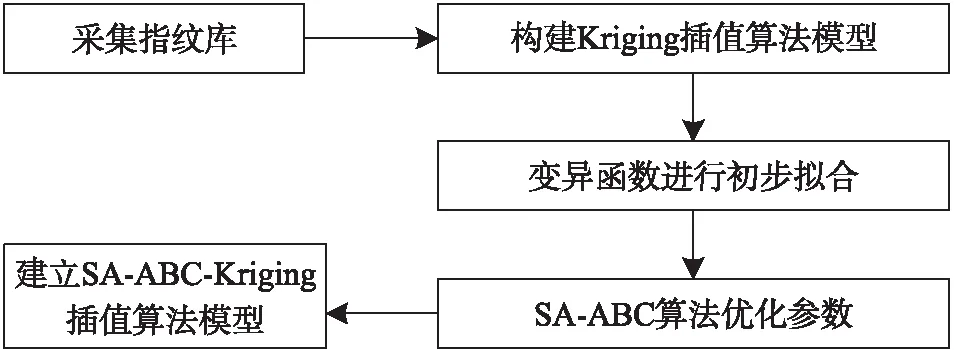
圖1 插值算法流程圖

4 煤礦井下指紋庫構建方法流程

煤礦井下指紋庫構建方法流程需要經過采集階段和插值階段,才能生成插值井下無線定位指紋庫,具體流程如圖2所示。

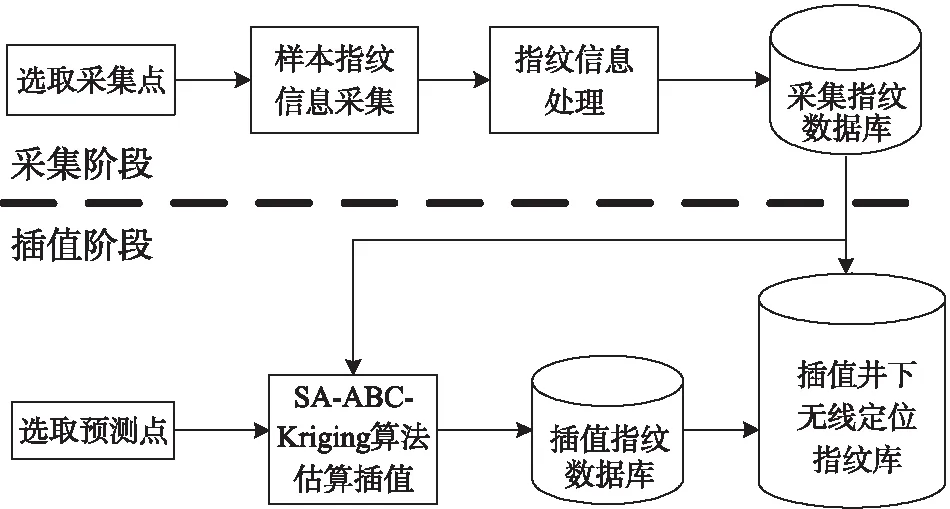
圖2 指紋庫構建流程圖

從圖2中可看出,采集階段首先井下巷道中選取采集點,其次采集點通過無線采集設備掃描各個AP節點的RSSI值傳送回服務器,為保障采集數據準確每個點采集20次,然后由服務器對采集點傳來20次RSSI值求其平均值與采集點的坐標位置進行式(16)組合,最后存放到采集指紋數據庫中,完成采集過程。

采集點的信息數據是按組合的方式存放數據庫中,其組合可以表示為:

xi={Xi,Yi,Ri1,Ri2,…,RiP}

(16)

式中P為AP節點數目,RiP表示第i個采集點接收到第P個AP節點的RSSI值,Xi,Yi為第i個采集點坐標位置。

插值階段首先根據采集指紋數據庫選取預測點,其次根據采集指紋數據庫生成SA-ABC-Kriging插值算法,再次調用所需觀測點的RSSI值,利用SA-ABC-Kriging插值算法對預測點RSSI值進行估算,并存放到插值指紋數據庫中,然后將采集指紋數據庫和插值指紋數據庫進行整合,最終生成插值井下無線定位指紋庫。

5 實驗結果分析

5.1 實驗條件及采集方法

實驗條件為貴州某煤礦井下500 m工業以太網已覆蓋的回風巷中,巷道截面寬度在4 m左右,井下實驗區工程平面如圖3所示。

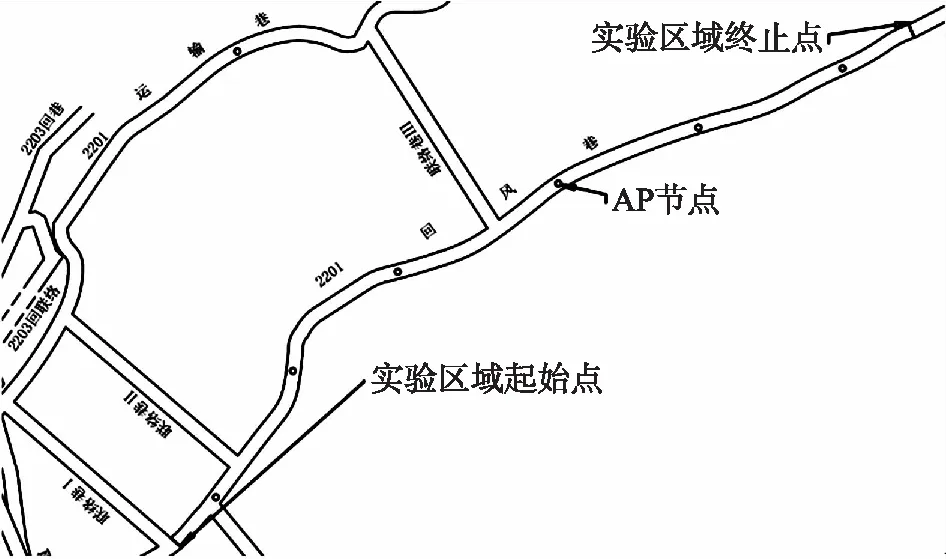
圖3 實驗區域工程平面圖

由圖3可看出,實驗區域為回風巷,在回風巷500 m區域范圍內共放置6個AP終端,AP節點之間距離在80 m內,可實現實驗區域無線全覆蓋。

采集方法:考慮到煤礦井下特殊地理環境,且井下巷道為二維平面。井下回風巷實驗區域長度500 m,井下截面寬度在4 m左右,為此把實驗區域分成為100個4 m×3 m小區域,小區域與小區域間距為1 m。在小區域內共有20個點,具體如圖4所示。

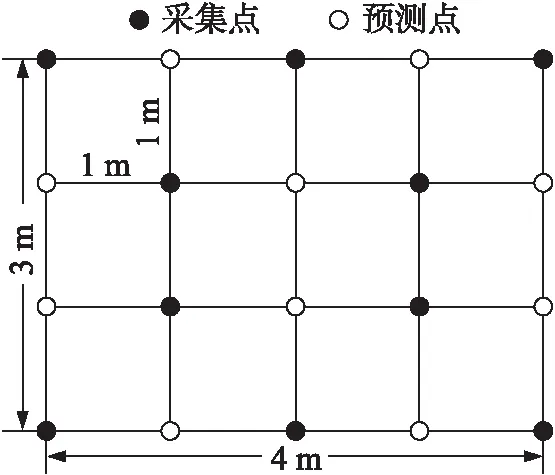
圖4 小區域指紋采集圖

由圖4可知,在小區域內選取10個點為采集點,10個點為插值估算預測點。由此可見整個實驗區域需要用到的采集點應為1 000個點,插值估算預測點應為1 000個點,建立完整井下定位指紋數據庫就需要2000個點的信息數據。

采樣階段:實驗人員佩戴自制無線采集設備到巷道中采集RSSI數據。其自制無線采集設備由主控芯片STC15W4K56S4、液晶顯示模塊LCD1602、無線芯片ESP8266EX和鋰電池供電模塊組成。該設備經過防爆測試,完全到達井下設備本質安全要求。自制無線采集設備工作原理:由主控芯片發送“AT+SCAN”(掃描AP)指令給無線模塊,無線模塊立即掃描當前位置處各個AP節點返回信息數據(包括IP地址,MAC地址和接收的信號強度指示RSSI值),主控芯片對該信息數據進行處理后,通過無線網絡傳輸給服務器。

為檢驗SA-ABC-Kriging插值算法的性能,實驗人員按照式(16)存放方式和逐點采集方法,點與點之間距離1 m,把實驗區域可采集2 000個點的信息數據全部采集完成,并存放到原始井下無線定位指紋庫。再從該數據庫中按照小區域采集方法把1 000個采集點的信息數據提取出來,組成采集指紋庫。

在完成2 000個點的采集任務后,實驗人員又重新隨機采集100組測試數據,存入測試數據庫,為檢驗性能提供數據支撐。

插值階段:首先根據100個小區域選取出1 000個預測點,其次根據采集指紋數據庫生成Kriging插值算法模型,對SA-ABC算法初始化,設置蜂群總數SN=60,蜜源的數量N=30,蜜源未更新次數limit=100,初始溫度T0=600,終止溫度Tmin=0,退火系數β=0.96,最大迭代數Kmax=800,迭代數k=0,收斂精度ε=0.01,然后根據SA-ABC-Kriging插值算法流程建立算法模型。

首先從采集指紋數據庫調用所需采集點的RSSI值。其次利用SA-ABC-Kriging插值算法對每個預測點RSSI值進行20次估算。再次用20次估算出的RSSI值,求出該預測點的RSSI平均值,已確保每個預測點的RSSI值更精確。然后再將預測點的RSSI平均值存放到插值指紋數據庫,并將采集指紋數據庫和插值指紋數據庫進行整合,最終生成插值井下無線定位指紋庫,完成插值過程。

5.2 性能分析

為檢驗樣子本文提出插值算法的插值精度,利用K最鄰近算法[20]KNN(K-nearest neighbor)和加權K最鄰近算法[21]WKNN(WeightedK-Nearest Neighbor)兩種算法驗證原始井下無線定位指紋庫和插值井下無線定位指紋庫的性能。

利用測試數據庫中信息數據,帶到KNN和WKNN算法進行在線定位,其K設為3。經過50次調用測試數據庫中100組測試數據定位運行,統計兩個井下定位指紋數據庫在2 m內的定位誤差累計概率,其結果如表1所示。

表1 指紋庫2 m定位誤差累計概率對比單位:%

從表1可看出,原始井下無線定位指紋庫和插值井下無線定位指紋庫定位精度基本一樣。再利用KNN算法進行定位,設K為5。經過50次調用測試數據庫中100組測試數據定位運行,統計兩個井下定位指紋數據庫在3 m內的定位誤差累計概率,其結果如表2所示。

表2 指紋庫3 m定位誤差累計概率對比單位:%

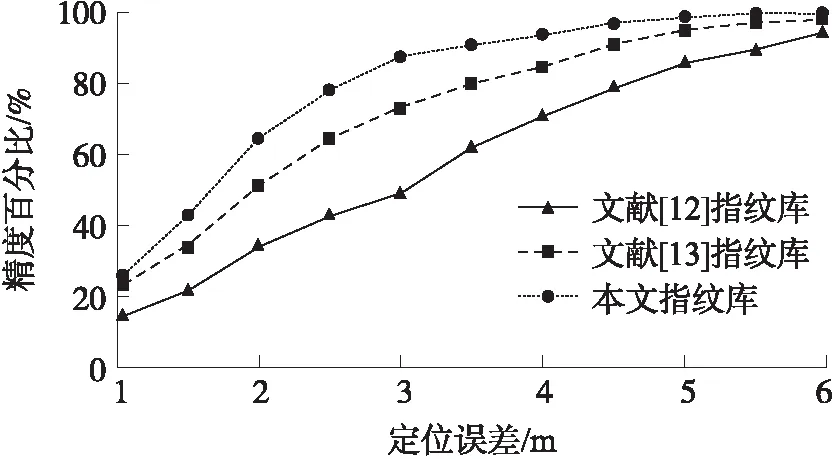
圖5 3種指紋庫定位精度對比圖

從表2可看出,插值井下無線定位指紋庫可以達到原始井下無線定位指紋庫定位精度。由此可見采用本文的方法構建井下指紋庫,可使人工采集信號強度的工作量減少50%,且指紋庫定位精度不變。

將文獻[12]的反距離加權插值法建立文獻[12]指紋庫、文獻[13]的克里金插值算法建立文獻[13]指紋庫、本文提出SA-ABC-Kriging插值算法建立插值井下無線定位指紋庫,三種插值指紋庫采用WKNN算法,設K為3。經過100次調用測試數據庫中100組測試數據對三種指紋庫定位運行,得到其定位性能如圖5所示。

從圖5可以看出,文獻[12]指紋庫采用WKNN算法的定位誤差較大,定位精度函數收斂性差;文獻[13]指紋庫定位性能優于文獻[12]指紋庫,但定位精度函數收斂較慢;而本文指紋庫采用WKNN算法定位精度最優,定位精度函數收斂最快。根據上述實驗結果,對比三種指紋庫定位誤差數據,得到定位誤差對比如表3所示。

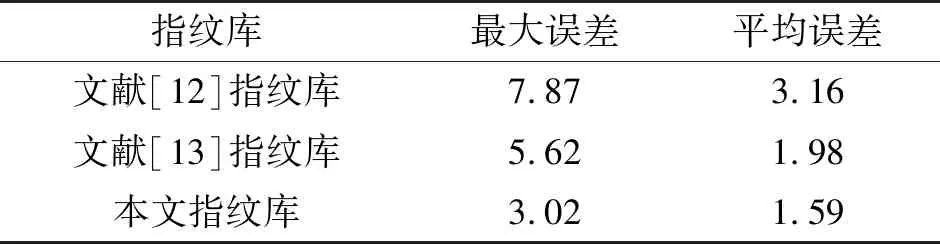
表3 3種指紋庫定位誤差對比表 單位:m

由表3可知,文獻[12]指紋庫定位平均誤差為3.16 m,文獻[13]指紋庫定位平均誤差為1.98 m,本文指紋庫定位平均誤差為1.59 m;所以本文提出SA-ABC-Kriging插值算法建立插值井下無線定位指紋庫比文獻[12]指紋庫定位精度提升49.68%,比文獻[13]指紋庫定位精度提升19.70%。

6 結論

本文針對煤礦井下無線指紋定位技術中離線采集階段構建指紋庫,需要大量采集工作的問題,提出了一種采用SA-ABC-Kriging插值算法構建井下指紋數據庫的方法。在實驗定位區域內采集少量的指紋庫,利用采集指紋數據庫構建Kriging插值算法模型,通過模擬退火人工蜂群混合優化算法對理論變異函數搜索全局最優解,從而建立SA-ABC-Kriging插值算法模型;再利用采集指紋數據庫中觀測點的信息數據通過插值算法模型估算出預測點的信息數據,建立插值數據庫,最后將采集指紋數據庫和插值指紋數據庫生成插值井下無線定位指紋庫,該構建方法提升未測量點的插值精度,大幅減少構建指紋庫所要指紋的采集量。通過實驗表明,本文方法在插值精度和定位精度上都優于傳統Kriging插值算法,在定位精度不變的情況下可將指紋庫采集工作量減少50%。

在接下來工作中,對SA-ABC-Kriging插值算法進行優化,提升算法性能,進一步提高插值精度和定位精度。