復雜網絡關鍵節點組識別問題模型和算法研究*

江 成，張 軍，盧 山

首都經濟貿易大學 信息學院，北京 100070

1 引言

隨著科技進步和全球一體化進程加速，人們日益處于各種復雜網絡中。例如，互聯網網絡、電力和交通網絡、經濟和金融網絡以及社會網絡等。這些網絡中存在一些對結構和功能影響程度更大的特殊節點，通常被稱為關鍵節點。這些關鍵節點在網絡中雖然數量不多，卻可以快速波及并影響網絡中的大部分節點[1]。例如，TOMsInsight團隊針對2014年“冰桶挑戰”形成的社會網絡數據分析發現：53%名人將相關視頻、圖片和文字發布到社交網絡，被傳播展示占比高達99%，而47%非名人被傳播展示占比不到1%[2]。由此可見，社會網絡傳播中的關鍵節點——名人效應是非常顯著的。

關鍵節點組識別問題是指[3]：在資源有限的情況下，從給定的網絡圖G=(V,E)中選擇K個節點（V、E分別代表節點集和邊集，K為正整數），使得移除這K個節點后，剩余網絡的某種衡量指標（如離散程度或傳播效應等）最優化。關鍵節點組識別問題作為復雜網絡微觀層面的重要研究內容，直接關系到信息的傳播速度和影響范圍，吸引了管理學、信息科和物理科學等多個領域學者的共同關注，并得到了廣泛的應用。例如，流行病傳播網絡中，在醫療資源有限的情況下，對哪些關鍵個體優先接種免疫以最有效阻斷病毒大規模傳播的問題[4]；通信網絡中，對哪些影響力重要性用戶重點識別以提升網絡消息傳播效率的問題[5]；恐怖主義網絡中，選擇哪些關鍵恐怖分子使得其被定點清除后網絡的破壞程度最大，即最小化恐怖主義襲擊活動可能性的問題[6]；交通網絡中，選擇哪些關鍵基礎設施重點保護，使得不致于因為意外原因而導致網絡大面積癱瘓的問題[7]。此外，關鍵節點組識別問題在電力系統關鍵部件保護[8]，生物網絡關鍵蛋白和基因的識別[9]，社會網絡意見領袖挖掘[10]等領域也有著重要應用。總結國內外已有研究可見，目前關鍵節點組識別問題研究主要是基于仿真模擬、指標度量和數學建模三種方式開展的。

在仿真模擬方面，已有研究大多借鑒流行病學中的疾病傳播模型來模擬網絡中節點的影響力傳播。因而，在這種類型方法下，復雜網絡關鍵節點組識別問題經常被等同于節點影響力最大化問題[11]。如Saito等基于SIS（susceptible infected susceptible）疾病傳播模型構建了一個多層的圖結構，用于識別社會網絡中最具影響力的節點[12]。Salamanos等通過圖采樣方法來識別復雜網絡中最具影響力的節點，并基于SIS和SIR（susceptible infected recovered）疾病傳播模型進行實驗模擬[13]；王禎駿等提出了一種融合內容信息和動態時間特性的影響力傳播模型，并借助該模型識別社會網絡中最有影響力的用戶[14]；張云飛等針對多個影響力同時傳播且影響力間存在促進傳播關系的情況下，對關聯影響力傳播最大化問題進行建模，并提出基于節點激活貢獻估計的求解算法[15]。

在指標度量方面，基于圖論的指標經常用來評價節點的重要性，例如，節點的中心度[16]、節點的介數[17]、節點的緊度[18]、節點的特征值[19]、K殼分解[20]等。然而這些指標只能反映網絡的單一屬性，忽略了整體結構和功能。為此，Borgatti從網絡的整體結構出發，提出了衡量網絡離散程度的專用度量指標DF，但直接優化DF因計算復雜度高而缺乏實際操作的可行性，因此其采用貪婪搜索方法對DF求解[3]。總體來看，指標度量方法反映了網絡拓撲的局部特性或全局特性，設計容易，簡單直觀。但是，按照指標對單個節點重要性排序結果選擇的前K個節點組合，往往并不是復雜網絡整個最優的K個關鍵節點集合[21]。

近年來，基于數學建模的方法逐漸得到國內外相關學者的關注。例如，Arulselvan等率先提出了整數線性規劃模型，通過最小化剩余網絡中連通分支的個數識別稀疏網絡中的關鍵節點集合，奠定了關鍵節點組識別問題的主流模型地位[22]。由于在求解精度上較基于仿真模擬和指標度量的方法更占優勢，該模型得到了學者們的關注，并且衍生出一些變體模型，例如最大化剩余網絡連通分支的個數[23-24]和最小化最大連通分支中的節點個數[25]等。此外，現有研究已經證明關鍵節點組識別問題是NP難問題[22]，因此基于貪婪搜索[26]、遺傳算法[27]、模擬退火[28]的一些啟發式算法也被提出來用于求解這些識別模型。更多關于關鍵節點組識別的研究方法請參考文獻[29-31]。

根據以上分析可見，現有的關鍵節點組識別方法較多，但各有側重。其中，基于仿真模擬的方法側重于從功能性傳播角度研究節點影響力，而對網絡整體結構的穩定性考慮不足；基于指標度量的方法，因其簡單直觀，計算復雜度較低，成為目前主要的識別方法，但其更適合于節點重要性排序問題[32-34]，對多個關鍵節點集合的識別問題評價不夠全面。而在數學建模方面，盡管已有研究在關鍵節點組識別問題上已經取得了顯著的成果，但是當前模型方法單一，并且現有的整數線性規劃模型本身存在不能夠區分連通分支內部結構的缺陷。

為此，本文從網絡的整體結構和功能出發，對復雜網絡關鍵節點組識別問題模型和算法進行研究，本文的主要貢獻如下：

（1）構建基于0-1二次約束二次規劃的關鍵節點組識別模型，通過最小化二階路徑內連通節點對的個數，實現區分連通分支內部結構的能力。

（2）提出兩種模型求解方法：一種是松弛為半正定規劃模型并利用內點算法求解，這種方法適用于小規模網絡的近似求解；另一種是設計貪婪搜索和局部置換相結合的啟發式算法，用于大規模網絡中的關鍵節點組識別。

（3）進行了大量人工隨機圖和真實復雜網絡數據集的實驗分析，驗證了所建立模型和算法的正確性和有效性。

2 相關工作

Krackhardt構建了用于計算每個連通分支內部連通節點對個數的度量指標[35]，如下所示：

式中，sk表示移除關鍵節點后剩余網絡中第k個連通分支中的節點個數。該指標計算簡單，計算復雜度較低，可以通過枚舉方法求解，但其忽視了連通分支的內部結構。在此基礎上，從網絡的整體結構出發，文獻[3]提出了衡量網絡離散程度的專用指標DF，定義如下：

式中，dij表示節點對i和j之間的最短路徑，DF∈[0,1]，且DF值越大，網絡的離散程度越大。DF指標雖然設計比較完善，但因其計算復雜度高，導致對其直接優化缺乏實際操作的可行性。

在Krackhardt指標基礎上，Arulselvan等建立了最小化剩余網絡連通節點對個數的整數線性規劃模型（integer linear programming，ILP）[22]，以便更好地洞察和深入理解關鍵節點組識別問題。然而，該模型和其衍生出的變體模型均存在不能夠區分連通分支的內部結構的缺陷，這一問題直接導致了實際優化效果并不理想。

3 模型規劃

為解決當前主流的整數線性規劃模型對連通分支內部結構的考慮不足，本文將基于DF指標建立數學模型，并提出新的計算解決方法。

3.1 模型的建立

基于0-1二次約束二次規劃（quadratically constrained quadratic programming，QCQP）建立模型，具體規劃如下：

其中，A是網絡的鄰接矩陣，如果節點i和j是鄰居節點，則aij=1，否則aij=0；vi=1表示節點i作為關鍵節點被移除，否則，vi=0；xij=1表示在移除關鍵節點后剩余網絡中節點i和j是鄰居節點，否則xij=0。此模型的目標函數是最小化剩余網絡中二階路徑內連通節點對的個數；約束（3）重新計算了移除關鍵節點后剩余網絡的鄰接矩陣，即如果節點對i和j在原網絡中是鄰居節點，但節點i或j被作為關鍵節點移除的話，則節點i和j之間的邊消失，并且這兩個節點在剩余網絡鄰接矩陣中對應的值為0；約束（4）表示在資源有限的條件下，被移除的關鍵節點個數不能超過K個。約束（5）約束模型為0-1非線性規劃模型。

3.2 模型與DF指標的關系

（1）當網絡結構為完全圖時，誤差為0；

（2）當網絡結構為星型網絡時，目標引入的誤差也為0；

4 算法求解

由于QCQP是非凸的二次規劃模型，為了高效求解，本文采取兩種求解途徑：一種是將其松弛為半正定規劃模型進行求解；另一種方法通過設計啟發式算法加以求解。

4.1 半正定松弛求解方法

這里對QCQP模型寫成矩陣表示形式，并松弛為半正定規劃模型（semi-definite programming relaxation，SDPR）的形式如下：

這里，W為將QCQP模型寫成矩陣形式的系數矩陣。y=(x11,x12,…,x1n,x21,x22,…,x2n,…,xn1,xn2,…,xnn)。利用商用軟件Matlab調用Gurobi接口中的內點算法，可以快速求解SDPR模型。需要注意的是，這種快速求解的松弛方法只提供了QCQP模型問題最優解的一個下界。當然，可以在此下界的基礎上，進一步設計分支定界算法求取最優解。

4.2 啟發式算法求解

采用貪婪搜索和局部置換相結合的思想，設計了一種新的啟發式算法。

算法1QCQP模型啟發式算法

輸入：網絡圖G和關鍵節點組個數K。

輸出：關鍵節點組集合和目標函數值。

（1）初始化一個空集S。若集合的元素個數小于K值，則最大化QCQP模型目標函數值，貪婪地向集合中逐個增加節點，直到該集合元素個數等于K。

（2）每次從S集合、V-S集合中各選取一個節點嘗試互換，進行2節點交換的局部搜索。如果交換能夠減少目標函數值，則進行互換，否則不互換。直至遍歷所有2節點交換組合。

（3）返回目標函數值最小下的節點組合S，以及相應的目標函數值。

4.3 復雜度分析

松弛求解方法的時間復雜度為O((n3.5)4)，計算成本較高，只適合小規模網絡的關鍵節點組識別。而啟發式算法的計算復雜度為O(n3)，適用于識別較大規模網絡的關鍵節點組識別。如果需要進一步降低算法復雜度，可以結合群體智能算法加以優化。

5 實驗分析

本章選取了多組不同規模的隨機圖和真實網絡數據集進行實驗，其中人工數據集可以通過圖模型隨機生成，而真實數據集可以從佛羅里達大學開源數據庫中下載獲取[36]。由于關鍵節點組識別問題限定在資源有限的條件下，因此本文討論的實驗結果限制在K≤|V|/2條件下。本文采用的松弛求解方法的編程語言為Matlab，調用Gurobi和CVX接口；啟發式算法求解的編程語言為Java。所有編程語言的實驗運行環境是1.70 GHz英特爾驍龍處理器，16 GB內存，Windows操作系統。

5.1 人工網絡實驗

為了驗證模型的魯棒性，本文選取了多種連接結構的網絡圖進行實驗，包括Erdos-Renyi圖[37]、Geometric圖[38]、Sticky 圖[39]、Range因果圖[40]和 Kleinberg圖[41]，并且每種類型網絡都隨機選取了不同的規模。雖然可以比較K≤|V|/2的結果，直至DF=1為止。但由于空間所限，此處僅針對Erdos-Renyi(|V|=14,|E|=36)列出全部結果，如表1所示。其余實驗數據集僅列出K≤5的結果，如表2～表5所示。其中，K為所識別關鍵節點的個數，Obj為移除關鍵節點后的模型目標函數值，T為運算執行時間，度量時間為毫秒（ms），DF指標用來評價識別結果的好壞，上標“*”表示性能比較中占優的一方。以Erdos-Renyi圖為例，從表1中可以看出，盡管本文利用松弛方法只求得QCQP問題的近似解，但在大部分情況下，求解的效果都好于傳統的整數線性規劃模型。例如，表1中第3行表示了一個具有14個節點和36條邊的E-R隨機網絡，當關鍵節點個數為1時，ILP模型及其啟發式算法得到的目標函數值均為79，相應的DF值是0.419 4和0.413 9；而本文提出的SDPR模型及QCQP啟發式算法得到的目標函數值均為386，相應的DF值均為0.435 9。這說明SDPR模型和QCQP啟發式所識別的關鍵節點，被移除后造成的網絡離散程度更大，在識別效果上更為有效。當然，也存在ILP模型和啟發式勝出的少數情形，這是由于本文所提出的近似求解方法只求得SDPR模型的近似解，在某些情況下會略遜于ILP模型求得的最優解。但從表1～表5的整體實驗效果來看，SDPR模型和QCQP啟發式算法在大部分實驗情況下均取得了較好實驗效果。

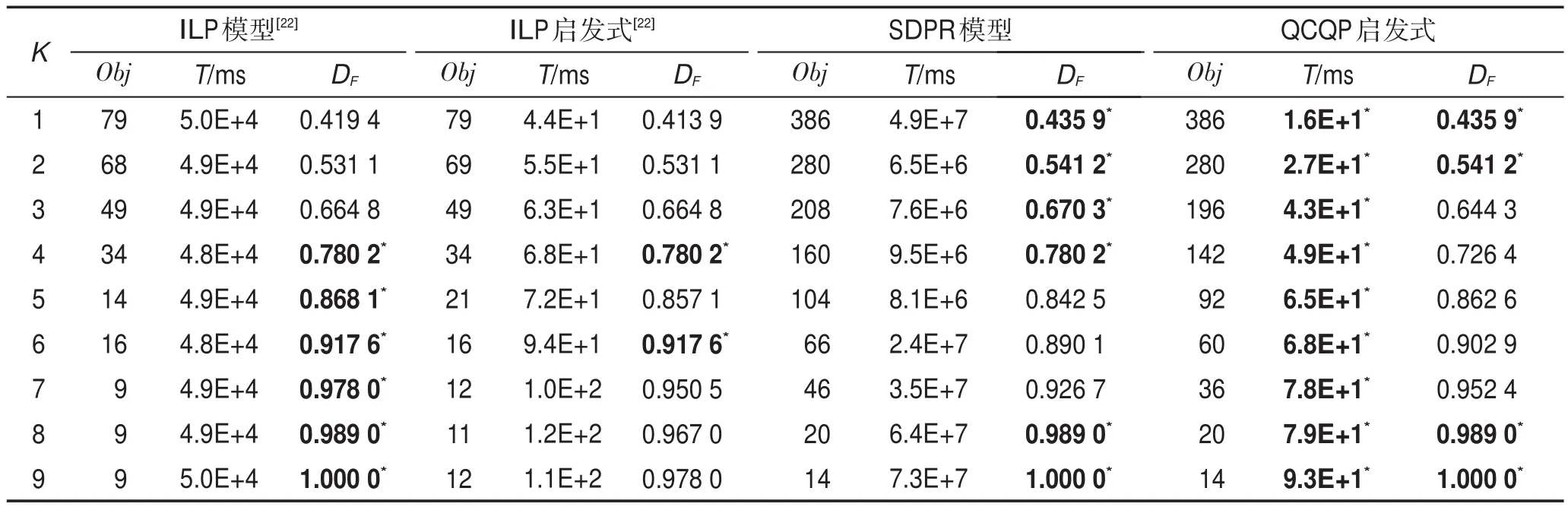
Table 1 Results on Erdos-Renyi(|V|=14,|E|=36)networks表1 Erdos-Renyi(|V|=14,|E|=36)網絡實驗結果

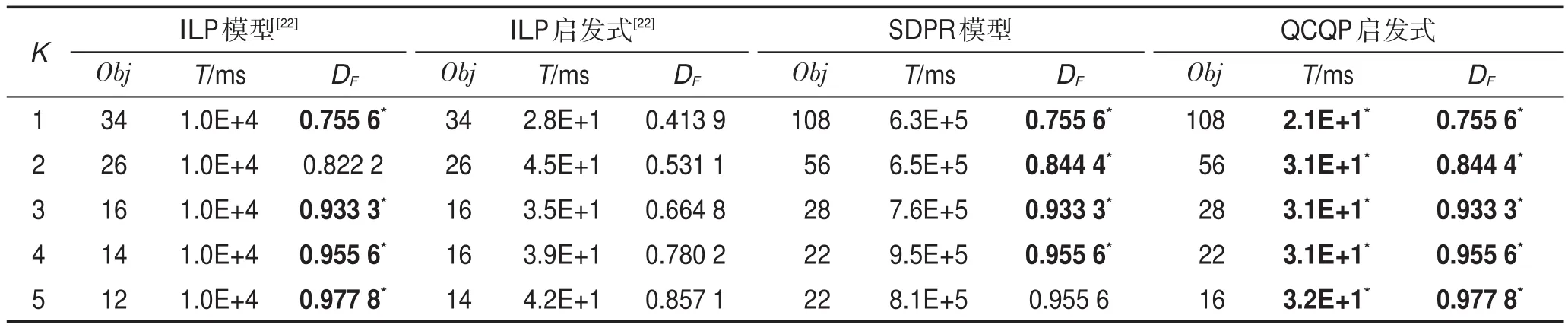
Table 2 Results on geometric(|V|=10,|E|=15)networks表2 Geometric(|V|=10,|E|=15)網絡實驗結果

Table 3 Results on Sticky(|V|=12,|E|=9)networks表3 Sticky(|V|=12,|E|=9)網絡實驗結果

Table 4 Results on Range dependent(|V|=14,|E|=15)networks表4 Range因果 (|V|=14,|E|=15)網絡實驗結果

Table 5 Results on Kleinberg(|V|=16,|E|=47)networks表5 Kleinberg(|V|=16,|E|=47)網絡實驗結果

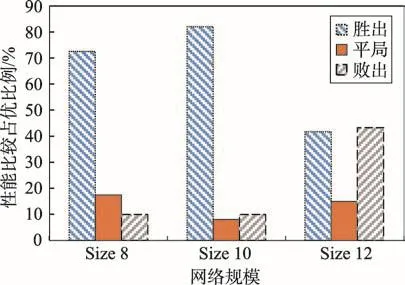
Fig.1 Statistical results on Erdos-Renyi networks圖1 Erdos-Renyi隨機網絡實驗統計結果

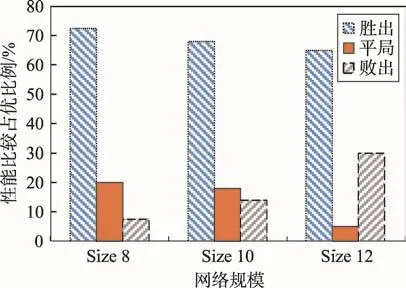
Fig.2 Statistical results on Range dependent networks圖2 Range因果網絡實驗統計結果

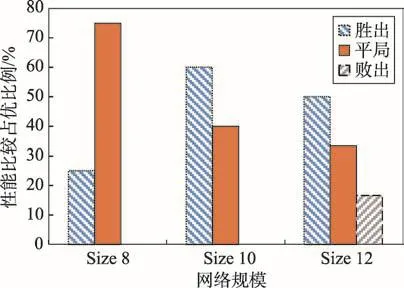
Fig.3 Statistical results on small world networks圖3 小世界網絡實驗統計結果

此外，針對Erdos-Renyi隨機圖、Range因果圖和小世界網絡圖，本文又分別隨機生成不同規模下（節點8、節點10和節點12）的網絡數據集進行實驗，統計分析本文所提出方法與傳統ILP方法比較情況下，勝出、平局和敗出各自所占的比例。圖1～圖3分別展示了在100組Erdos-Renyi隨機圖、Range因果圖和小世界網絡圖在節點規模為8、10和12規模下實驗的統計情況分布圖。從圖中可以看出，本文提出的方法在大多數情況下占優。

5.2 真實網絡實驗

為了驗證本文所提出算法的有效性，本文進一步選取了Can73通信網絡、Football115合作網絡、Jazz198音樂家社交網絡和Celegans453網絡標準數據集進行實驗。由于空間所限，此處僅列出K≤10的結果，從表6～表9可見，本文所提出的QCQP啟發式算法在大多數情況下識別的DF效果好于ILP啟發式算法的DF值，并且在計算時間上占優，QCQP啟發式算法的運行效率大約是ILP啟發式算法的102～103倍。

從表6～表9中可見，本文所提出的QCQP啟發式算法在大部分情況下效果占優。但由于QCQP啟發式求解的是QCQP模型的近似解，因此在個別點也存在不如ILP模型啟發式的情況，后續可以進一步設計精確求解算法。為了能夠進一步從“實際角度”解釋關鍵節點，本文又基于“9?11”恐怖襲擊網絡進行實驗。將本文方法識別出關鍵恐怖分子群組，與“9?11”恐怖襲擊事件調查報告[42]所公布的恐怖分子地位進行比較驗證。實驗結果表明：本文方法所識別出關鍵恐怖分子頭目群組，與“9?11”恐怖襲擊事件調查中利用社交網絡度、介性和緊度分析得到的恐怖分子頭目吻合度較好，具體實驗的結果如表10所示。

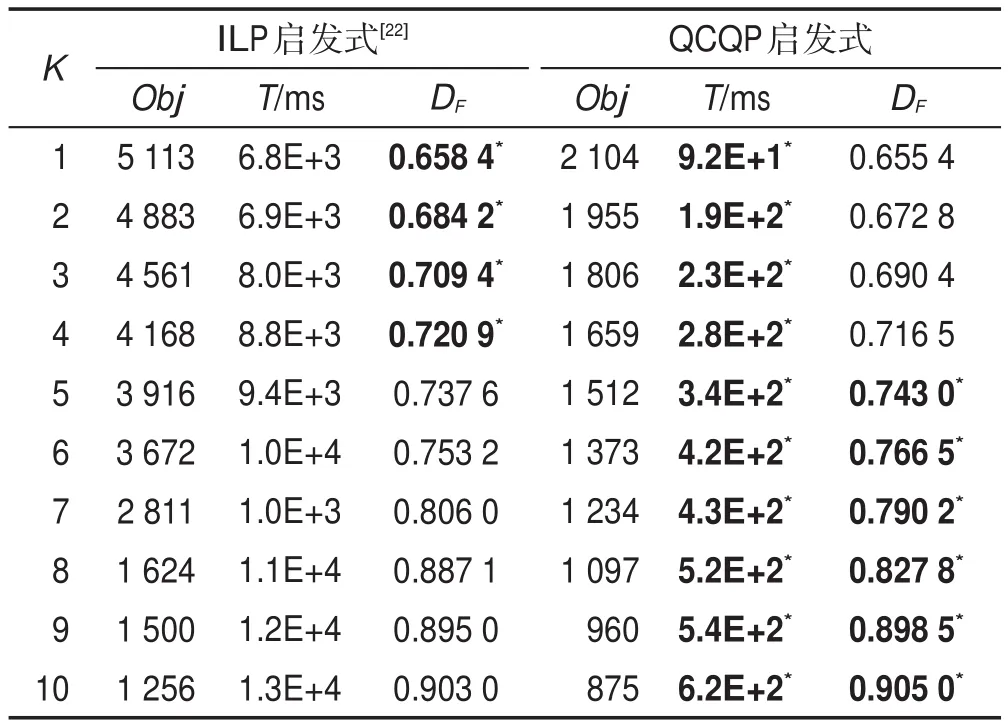
Table 6 Results on Can(|V|=73,|E|=47)networks表6 Can(|V|=73,|E|=47)通信網絡實驗結果

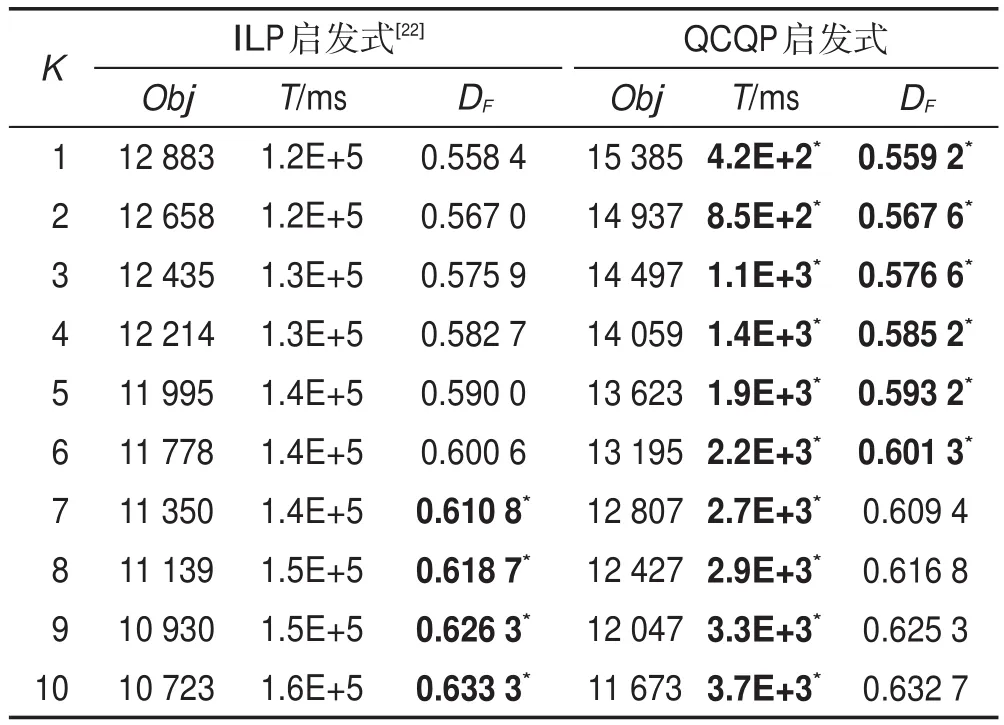
Table 7 Results on Football(|V|=115,|E|=47)social networks表7 Football(|V|=115,|E|=47)社交網絡實驗結果

Table 8 Results on Jazz(|V|=198,|E|=47)social networks表8 Jazz(|V|=198,|E|=47)社交網絡實驗結果

Table 9 Results on Celegans(|V|=453,|E|=2 025)networks表9 Celegans(|V|=453,|E|=2 025)網絡實驗結果

為了展示移除關鍵節點后網絡的變化情況，圖4～圖6以Can73通信網絡為例，分別可視化展示了ILP啟發式方法和QCQP啟發式算法在K=1、K=5和K=10的識別結果。

6 總結與展望

本文從網絡整體結構出發，提出了一種非凸的0-1二次約束二次規劃模型，模型的目標是最小化移除關鍵節點后剩余網絡中二階路徑內的連通節點對的個數，通過這樣的建模方法，實現了區分連通分支內部結構的能力。在此基礎上，本文又設計了兩種模型求解方法：一種是通過半正定松弛的方法識別小規模網絡中的關鍵節點組；另一種是設計了結合貪婪搜索和局部置換的啟發式算法，以適應大規模網絡的關鍵節點組識別。通過在多組不同規模的隨機網絡和真實網絡實驗，驗證了模型和算法的正確性和有效性。在未來的研究中，本文將擴展模型到大規模網絡、有向有權網絡以及動態網絡中進行識別應用。

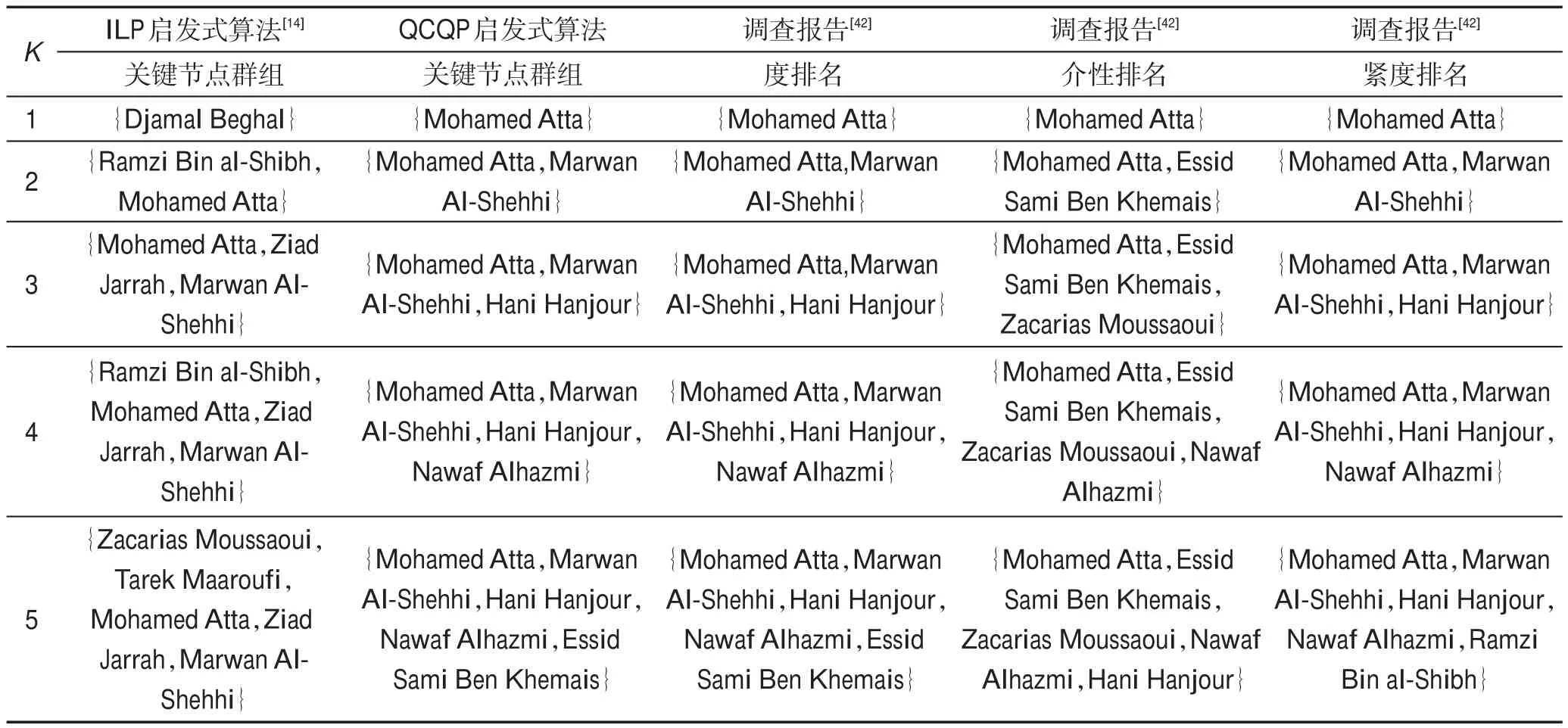
Table 10 Comparisons on“9?11”terrorist attack dataset(|V|=63,|E|=154)表10 “9?11”恐怖襲擊數據集（|V|=63,|E|=154）上的實驗比較

Fig.4 Experimental results on Can73 network for K=1圖4 Can73通信網絡上K=1時實驗結果對比

Fig.5 Experimental results on Can73 network for K=5圖5 Can73通信網絡上K=5時實驗結果對比

Fig.6 Experimental results on Can73 network for K=10圖6 Can73通信網絡上K=10時實驗結果對比