云科學工作流截止期限約束代價優化調度算法*

陳彥橦，裴樹軍，苗 輝

哈爾濱理工大學 計算機科學與技術學院，哈爾濱 150080

1 引言

現代科學在天文學、地球科學、生物信息學等不同研究領域中運行日益繁雜的大規模科學應用，以模擬和分析現實世界的活動，而科學工作流已被證實是建模和管理這些復雜問題的最有效手段[1]。科學工作流通常由一組通過控制和數據依賴鏈接的粗粒度并行計算任務組成。隨著數據生產速度的提升和計算系統的日益復雜化，科學工作流越來越體現為大數據形式，如計算密集型和數據密集型[2]。科學家通常將科學工作流部署在傳統的分布式執行環境，如集群和網格等平臺上，然而系統的建立所付出的代價是非常高昂的，且資源的擴展性較差[3]。近年來隨著云計算技術的發展，其在性能和成本方面為科學工作流提供了相當好的解決方案，云以虛擬機（virtual machines，VM）的形式為用戶提供計算資源，與傳統的分布式執行環境相比，具有無限的計算和存儲資源、資源按需提供以及允許用戶彈性地獲取和釋放資源等優點。雖然云環境有很多優勢，但仍然存在某些需要通過預期調度策略解決的特定問題，例如虛擬機實例采集延遲、虛擬機資源的異構性及動態按需提供等問題。

工作流的調度主要包含兩個層次：一是任務與虛擬機實例之間的映射；二是單個虛擬機上任務的順序執行。調度算法的眾多性能指標中，用戶最關心的兩個指標為工作流的完成時間和執行代價。分布式資源上的工作流時間代價優化調度是一個NP-hard問題，對于這類問題，利用基于啟發式和元啟發式的調度算法能夠取得近似最優解[4]。

相關研究中，文獻[5-7]提出基于逆向分層的截止期限約束費用優化算法TCDBL（temporal consistency based deadline bottom level）和 PBCO（path balance based cost optimization），將截止期限分解到各層，使費用優化問題由全局轉化到局部。在此基礎上提出CACO（communication aware cost optimization）算法，采用動態規劃收集任務與虛擬機匹配時產生的時間碎片，改善費用優化效果，但并未為任務設定優先級來找到最佳調度順序。文獻[8-9]提出了基于部分關鍵路徑的調度算法IC-PCP（IaaS cloud partial critical paths）和CPC（critical path cut），將局部關鍵路徑中的任務都安排在同一個費用最低的VM實例上，避免了任務間的通信成本，但多條部分關鍵路徑分配到不同VM上時，由于任務間的數據傳輸將導致較低的任務調度成功率。文獻[10-11]提出自適應調度算法 MOEA（multi-objective evolutionary algorithms）和UQMM（uncertainty-based quality of service Min-Min），用于在異構多云環境中實現用戶定義約束的任務調度，使算法具有更高的適用性。

近年來，很多學者側重于利用智能搜索算法解決調度問題。文獻[12-13]提出基于蟻群的元啟發式算法，放寬截止期限引導搜索朝著約束方向優化。文獻[14]提出基于粒子群的最優調度算法，利用關鍵路徑進行粒子初始化和搜索階段的篩選處理，提高搜索結果的精度和降低搜索的計算時間。文獻[15]提出一種模擬退火遺傳改進算法SA（simulated annealing），將模擬退火算法與遺傳算法相結合，用以解決工作流的多目標優化問題。雖然這些方法都具有良好的表現，但與其他基于啟發式的方法相比，智能搜索算法在初始化階段耗時過多。

針對異構云環境下科學工作流截止時間約束的代價優化調度問題，本文提出了基于約束關鍵路徑的代價優化算法（cost-optimized scheduling algorithm based on constrained critical path，CSACCP）。算法分為兩個階段：第一階段設定任務的向上權值，根據權值將工作流分解為約束關鍵路徑（constrained critical path，CCP）集合。第二階段在滿足截止期限約束的條件下，通過最小費用增長代價和及時完成的VM選擇策略，結合首次適應插入算法，實現每條約束關鍵路徑與最優VM的匹配。

2 系統模型

2.1 科學工作流模型

科學工作流通常用有向無環圖（directed acyclic graph，DAG）進行描述，表示為G=(T,E)，其中T={t1,t2,…,tn}表示一個含有n個任務節點的有限集，E={eij|ti,tj∈T}表示任務之間數據依賴關系的有限邊集。每條數據依賴邊eij=(ti,tj)代表任務ti和任務tj之間的數據控制依賴關系，其中任務ti稱為tj的直接前驅，任務tj是ti的直接后繼。用pred(ti)表示任務ti的直接前驅集合，succ(ti)表示任務ti的直接后繼集合。|eij|表示兩個任務之間的數據傳輸量。

在一個給定的DAG工作流中，一個不存在任何前驅任務的任務稱為入口任務tentry，一個不存在任何后繼任務的任務稱為出口任務texit。若一個DAG中存在多個入口任務或多個出口任務，則需要增加一個虛擬任務（計算和通信開銷都為0）來保證DAG在進行調度時有唯一的入口任務和出口任務。

一個擁有11個任務的簡單工作流如圖1所示，每個節點代表一個任務，邊上的權值代表兩個任務之間的數據傳輸量。

Fig.1 Sample workflow圖1 工作流示例

2.2 云資源模型

云資源以m種異構的VM形式提供VMSET={VM1,VM2,…,VMm}，每個VM類型，在其CPU性能、內存容量和資源定價等方面都擁有自身配置。資源定價基于Amazon EC2中按需提供的定價模型，用戶根據VM租賃時間間隔（timeinterval）的數量付費。同時當VM租用時，需要一個引導時間對VM進行初始化以便用戶使用，用戶可根據需要部署相應的軟件資源。

由于云服務商提供獨立于VM生存期的存儲服務，例如EBS（elastic block store），因此當輸入數據文件傳輸到相應的存儲資源時，要執行子任務的VM不需要處于活動狀態。此外由于用于存儲輸入輸出數據的存儲資源所需的成本與調度算法無關，因此在此模型中未考慮。假設所有計算和存儲服務都位于同一數據中心或區域，計算服務之間的平均帶寬基本相同，用β表示。當兩個具有數據依賴關系的任務所選的VM實例不同時就會產生通信開銷，則此時兩任務之間通信開銷如式（1）所示：

表1給出了實驗中使用的Amazon EC2所提供的5種VM資源類型的相關參數，其中一個ECU單元相當于1 GHz Xeon CPU的性能。

Table 1 Types of VM表1 VM類型

將VMSET中每個VMk定義為一個二元組(EXT(ti,VMk),Cost(VMk))，其中EXT(ti,VMk)表示任務ti在資源類型為VMk上的預期執行時間，如式（2）所示，Cost(VMk)表示單位時間租賃成本。

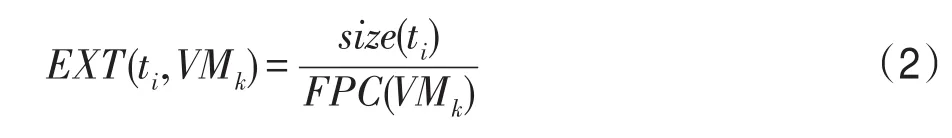
其中，size(ti)表示任務ti的大小，以浮點計算的運行次數度量；FPC(VMk)表示VMk的計算能力，以每秒進行的浮點運行次數度量。

2.3 計算平臺模型

本文使用與文獻[16]中相似的計算平臺模型，如圖2所示。用戶提交工作流及相關的服務質量（quality of service，QoS）要求，例如截止時間期限和資源需求到工作流管理系統。工作流管理系統由三個主要模塊組成：資源調配模塊、工作流調度模塊和執行管理器。資源調配模塊分析工作流結構以預估所需資源量，動態地向云服務商申請資源，并在租賃期結束時釋放資源。工作流程調度模塊與執行管理器協調，完成工作流任務與資源之間的映射，并由資源管理器執行。

Fig.2 Scheduling system model圖2 調度系統模型

工作流管理系統維護一個資源池Active_VMs信息列表，資源池信息列表中存儲每個申請到的資源實例的類型、開始時間和結束時間，如式（3）所示：

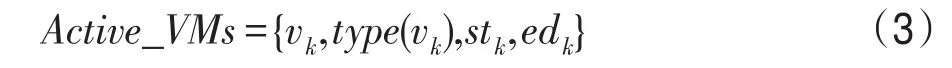
2.4 調度目標

工作流調度目標定義如下：

為工作流G規劃一個時間表S，在總執行時間makespan不超過工作流截止期限D的條件下，最小化運行工作流的執行代價CostTotal，如式（4）所示：

3 CSACCP算法設計

本章首先介紹與算法有關的基本定義，然后設計CSACCP調度算法。算法首先調用Gen_CCPSET將工作流分解成CCP集合，然后通過CheapestMap算法實現每條CCP與最優VM的匹配，以期在異構云環境中在滿足用戶截止期限的約束下盡可能減少執行代價。

3.1 基本定義

定義1MXT(ti)表示任務ti的最小執行時間，定義為其在VMSET中所有資源類型上最小執行時間，其計算公式如下：

定義2EST(ti)表示任務ti的最早開始時間，定義為其所有直接前驅被安排在執行時間最小的VM上，并且所有所需的依賴數據都已傳遞到ti。其計算公式如下：

定義3EFT(ti)表示任務ti的最早完成時間，定義如下：

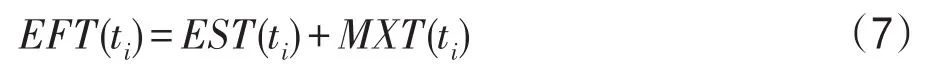
定義4MEXT_G表示工作流最早完成時間，即出口任務的最早完成時間，計算公式如下：

定義5XFT(ti)表示任務ti被調度到VM實例為vq上的預期完成時間，計算公式如下：

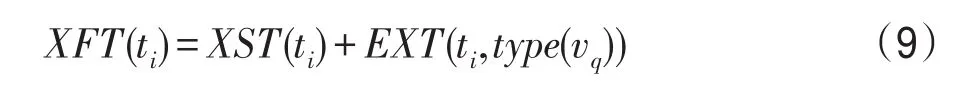
定義6XST(ti)表示任務ti被調度到VM實例為vq上的預期可開始時間，只有在所有直接前驅執行完畢且依賴數據傳輸到vq時才可開始，計算公式如下：

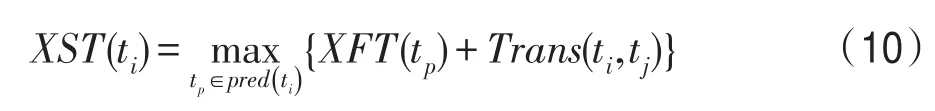
定義7XIDT(vq)表示VM實例vq的預期空閑時間，其中tp為安排調度到vq上的最后一個任務，計算公式如下：

定義8XET(ti,VMk)表示從任務ti之后開始的關鍵路徑在VM類型為VMk上的執行總時間，計算公式如下：

3.2 CSACCP算法

3.2.1 Gen_CCPSET算法生成CCP

通常關鍵路徑是指工作流任務圖中從入口節點到出口節點的最長路徑。路徑的長度為節點的執行時間的平均值和沿該路徑的通信開銷的總和。當關鍵路徑上的任務首先被調度時，將產生有效的調度，但是關鍵路徑上的所有任務并非全都準備就緒。所有直接前驅已經為其調度處理的任務被稱為準備就緒任務。只包含準備就緒任務的一組任務構成了一條約束關鍵路徑CCP。每個CCP可以根據其任務的完成時間分配一個VM實例，將減少依賴數據傳輸時間。

HEFT（heterogeneous earliest-finish-time）[17]中將任務ti的向上權值rank定義為任務ti至texit的關鍵路徑長度，并根據rank的大小決定任務執行的優先級。從出口任務開始向上迭代計算每個任務的rank值，計算公式如式（13）所示：

考慮到出度高的任務若沒有及時執行會影響整個工作流的執行時間，CSACCP算法將向上權值進行改進，計算公式定義如下：

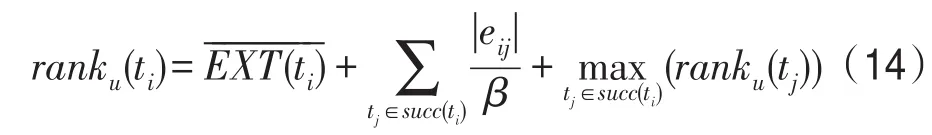
ranku與HEFT中的向上權值的差異在于聚合了任務直接后繼的通信時間，任務的出度越高優先級越高。

算法Gen_CCPSET用于生成CCP集合。首先從降序排列的權值集合中選取最大值任務，查找到其入度為1且權值最大的子任務，繼續向下尋找直到不存在入度為1的子任務，生成一條CCP。從權值任務集合中去除CCP任務，并在邊集合中去除CCP相關有向邊，重復上一步直到集合為空。算法描述如下：

算法1Gen_CCPSET(G=(T,E))

圖1中簡單工作流每個任務在三種VM類型上的執行時間及計算所得向上權值如表2所示。

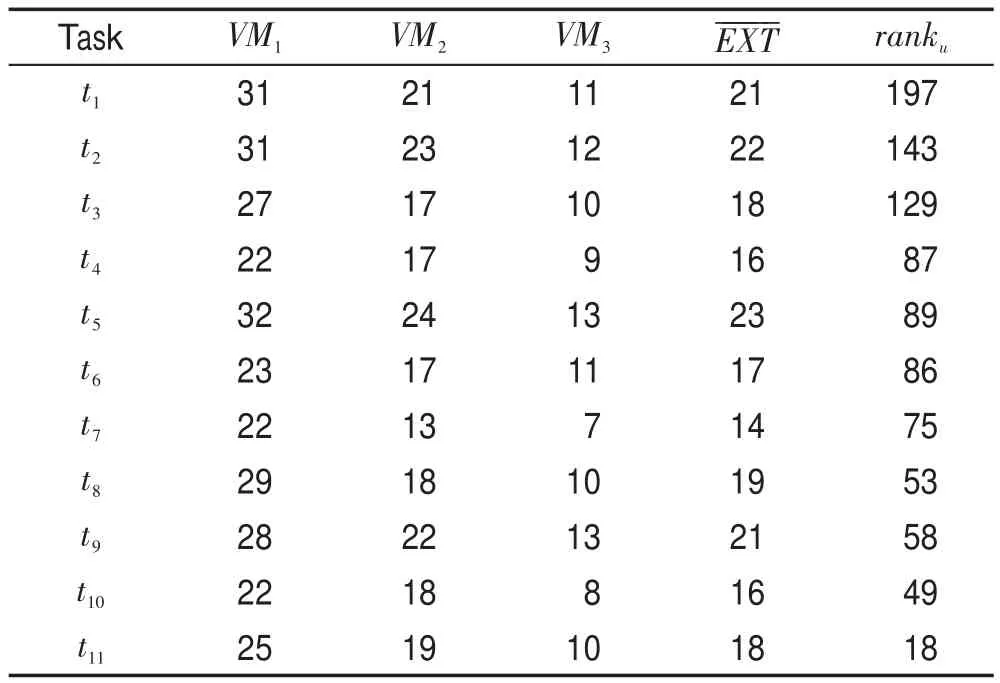
Table 2 Upward rank of workflow表2 工作流向上權值

則經過Gen_CCPSET之后生成的CCPSET為：

CCPSET={{t1,t2},{t3,t6,t9},{t5},{t4,t8},{t7,t10,t11}}

3.2.2 CheapestMap算法

CheapestMap算法接收CCPi及資源集合VMs作為輸入，并返回其最便宜的適用VM實例cheapestvm。

盡管最便宜的VM實例可能在其最晚完成時間之前完成任務，但它可能不是最佳選擇。這是因為任務選擇最便宜的VM實例，而不考慮其對后繼任務的影響，可能會強制后繼任務在更快的VM上執行，從而增加總體成本。因此，本文采用及時完成策略，將最便宜的適用VM實例定義為，在單個VM實例vk上，調度執行此CCPi及從其尾任務ti之后開始的關鍵路徑(最長路徑)，在滿足截止期限D的條件下使得費用增長代價mincost最小。

由于每個任務必須等待其直接前驅的依賴數據，因此在調度任務之間可能會形成空閑時隙。如果空閑時隙過多，則會產生資源浪費。因此為了提高資源的利用率同時進一步降低執行代價，算法首先考慮對空閑時隙的利用，采用首次適應（first fit）的回填策略，在滿足截止期限的前提下，將CCPi插入最合適的空閑時隙，此時最小費用增長代價mincost為0。

對于資源集合VMs中每個虛擬機實例vk，算法由CCPi中每個任務在vk上的XFT(tj)和XST(tj)來計算CCPi的預期結束時間XFTCCP(CCPi)和預期開始時間XSTCCP(CCPi)以及預期執行時間XETCCP(CCPi)，計算公式如下：

若其滿足工作流截止期限D，則計算vk的費用增長代價，最終返回最便宜的虛擬機實例cheapestvm。算法描述如下：

算法2CheapestMap(CCPi,VMs)

3.2.3 CSACCP算法

為了適應VM采集延遲launchdelay，算法將輸入預期的VM采集時間并相應地作出供應決策。由于VM終止延遲不會對工作流程的截止時間限制產生不利影響，因此本算法不考慮終止延遲。

算法首先評估MEXT_G并將其與用戶指定的截止期限D進行比較，如果D大于MEXT_G，算法會繼續尋找適當的調度時間表，否則會提示用戶修改截止期限D。一旦確定了用戶指定的截止期限的可實現性，算法調用Gen_CCPSET生成約束關鍵路徑集合CCPSET，再對集合中每條約束關鍵路徑調用CheapestMap，選取最便宜的VM實例進行匹配。

由于活動資源池Active_VMs并不一定滿足所需，則將VMSET中每種虛擬機類型新實例集合New_VMs與其合并形成備選資源集合VMs用于選取最便宜的虛擬機實例。若最終選取的實例屬于Active_VMs，將其調度到該實例上，并更新活動資源池狀態；若屬于New_VMs，考慮虛擬機實例采集延遲，在XSTCP(CCPi)-launchdelay時刻新建虛擬機實例，將其調度到新建虛擬機實例上并更新資源池狀態信息。算法描述如下：

算法3CSACCP

3.3 時間復雜度分析

為計算時間復雜度，假設工作流G=(T,E)由n個任務組成，數據依賴邊的最大數量為n(n-1)/2，云服務商提供m種異構的VM資源。CSACCP首先計算MEXT_G，判斷用戶定義截止期限的合理性，其時間復雜度為O(n2)。一旦確定用戶定義的截止期限是合理的，算法計算XET矩陣，為后續VM與CCP的匹配做準備，其時間復雜度為O(n2m)。接下來算法通過調用Gen_CCPSET算法生成約束關鍵路徑集合，由于需要計算任務的向上權值，其時間復雜度為O(n2m)。最后CSACCP算法為CCPSET中每條CCP調用時間復雜度為O(n2m)的CheapestMap算法進行虛擬機的匹配，考慮所有依賴性的時間復雜度為O(n3m)。此外由于云服務商提供的VM類型的數量是恒定的并且小到足以忽略，因此CSACCP算法的時間復雜度為O(n2+n2m+n3m)=O(n3)。

4 實驗結果及分析

4.1 實驗設置

工作流采用Juve等人[1]研究的4種不同科學領域中的工作流結構作為測試源，包括天文學領域的Montage、地震科學領域的Cybershake、重力物理學領域的LIGO和生物基因學領域的Epigenomics。每種工作流的大致結構如圖3所示，這些工作流具有不同的組成和結構特性。為了便于評估工作流算法，Bharathi等人[18]開發了一個Pegasus工作流生成器來生成類似于真實科學工作流的人工合成工作流，將諸如任務列表、任務之間的依賴關系、計算時間等信息存儲在XML格式的文件中。選取3種大小的工作流進行了測試：小型（約100個任務）、中型（約300個任務）和大型（約1 000個任務）。由于實驗結果相似，則結果圖表中只顯示大型工作流的實驗結果。為了對所提出工作流調度算法進行評估，本節利用仿真工具CloudSim[19]對由Pegasus生成的不同的工作流進行仿真測試。

Fig.3 Four workflow structures used in experiment圖3 實驗中所用4種工作流結構

假設云服務提供商提供5種不同類型的VM。虛擬機實例配置及處理能力基于Amazon EC2，參數如表1所示，不同虛擬機之間的平均帶寬設置為20 Mb/s，VM的采集延遲設置為97 s[20]。

每個工作流需要一個對應的截止期限來評估所提出的算法，太短的截止期限會導致大部分工作流無法及時完成，如果截止日期非常寬松，則有足夠的時間以較低費用完成工作流的執行。為了設定截止期限，通過式（18）將截止時間分布于嚴格、適度與寬松之間。

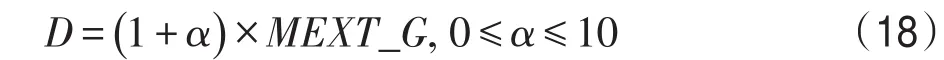
截止期限因子α從1開始考慮非常嚴格的截止期限（通常接近最快執行時間），最高為10的非常寬松的期限，且步長為1。

4.2 對比算法

為了驗證CSACCP調度算法的有效性，選擇ICPCP[8]和RCT（robustness cost time）[21]作對比算法，在考慮所有依賴性的前提下，3種算法時間復雜度均為O(n3)。

IC-PCP算法是針對本問題最常引用的算法之一。算法分為截止期限分布和規劃調度兩個階段，算法將用戶定義的截止期限分布在所有任務上，起始于將關鍵路徑上的關鍵任務在滿足截止期限的前提下，安排在最便宜的VM上執行以消除通信代價，然后通過遞歸計算關鍵路徑上未被調度的后續任務的關鍵路徑，重復以上步驟直到所有任務調度完成。但是IC-PCP算法并未考慮到VM的采集延遲。

文獻[21]中提出了一種健壯性的工作流調度算法RCT，該算法考慮了云環境中資源采集延遲，依據成本和時間的權重設定目標函數。基于部分關鍵路徑PCP（partial critical path），由健壯性類型定義的一定量的松弛時間被添加到PCP執行時間，每個PCP都有可行解集合FS（feasible solution），從FS中選擇適當的VM實例。

4.3 實驗結果分析

4.3.1 性能指標

為了評估被測算法，選擇使用以下性能指標：任務調度成功率SR（success rate）和標準化執行成本NEC（normalized execute cost）。

每個算法的任務調度成功率SR，計算為成功達到預定期限的模擬運行次數nk與模擬運行總次數ntotal之間的比率，定義為：

因為存在多種不同性質的科學工作流，所以需要一種標準化方法統一定義執行成本。本文首先考慮了在最后期限內失敗的成本，因此標準化執行成本NEC定義為：

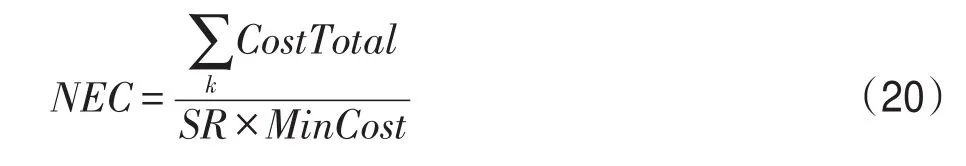
其中，CostTotal是滿足期限工作流的成本，已在式（4）中定義。MinCost為利用貪心策略將所有任務分配到最便宜的VM實例中的執行成本。

4.3.2 算法執行時間

表3具體介紹3種調度算法針對不同類型的4種工作流的平均執行時間。考慮所有任務依賴性的前提下，時間復雜度均為O(n3)，結果表明3種算法的執行時間相差不大。值得注意的是，在LIGO工作流中，CSACCP算法的執行時間相對其他算法有所降低。這是受工作流結構的影響，由于CSACCP算法執行時間主要消耗在為CCP查找最便宜的VM上，CSACCP將LIGO工作流分解為多個結構相似且執行時間較短的約束關鍵路徑，使大量的CCP更容易滿足首次適應的插入策略，減少了每條CCP在查找最便宜的VM時的計算時間。因此執行時間有所降低，在大型工作流中較為明顯。

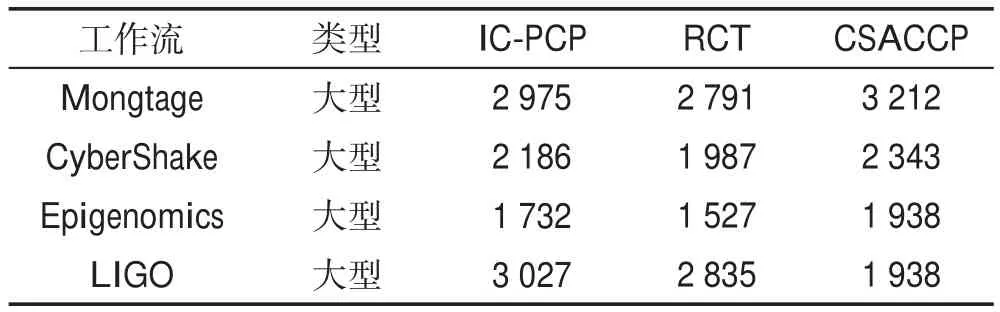
Table 3 Average running time of 3 scheduling algorithms表3 3種調度算法平均執行時間 ms

4.3.3 調度成功率

評估每種工作流在不同截止期限因子的情況下任務調度成功率，結果如圖4所示。

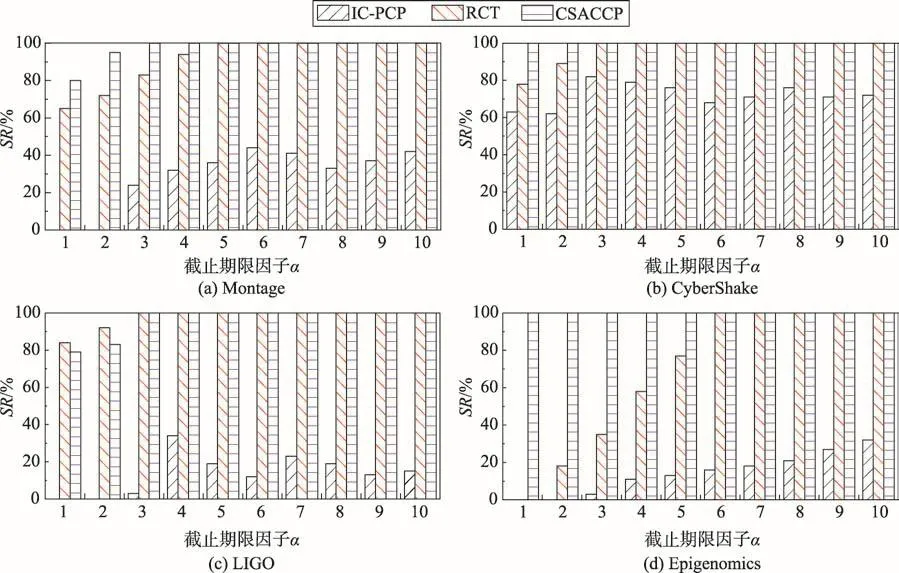
Fig.4 Scheduling success rate圖4 調度成功率

圖4顯示了截止期限因子α從1增加到10，每種算法的調度成功率SR。較低的成功率表明算法無法找到符合截止期限的完成時間。可以觀察到IC-PCP在α為1和2時，在大多數情況下都無法找到滿足截止期限的調度策略。這是因為算法首先遍歷工作流，在忽略任務間通信開銷的前提下，將整條關鍵路徑分配到一個最便宜的VM上。在后續的迭代選取剩余部分關鍵路徑并為其分配VM時，由于分配到不同VM上的任務間需要通信開銷，這將導致在嚴格截止期限下，已分配的關鍵路徑無法在預期的時間內完成，因此整體表現較差。

除Epigenomics之外，RCT和CSACCP在適度和寬松的截止期限內沒有明顯差異，但是CSACCP在嚴格的截止期限內比RCT有更好的表現。這是因為RCT將成本及執行時間設定目標函數，成本的優先級高于執行時間，這將導致在嚴格的截止期限內的表現不如CSACCP。尤其具有高并行度局部關鍵路徑的工作流Epigenomics，每條局部關鍵路徑都具有較長的執行時間。RCT優先考慮對執行成本的影響，在滿足最小費用增長的前提下，將多條局部關鍵路徑分配到一個VM上，忽視了對截止期限的影響，因此在嚴格的截止期限內無法找到合適的調度策略。而CSACCP設定了任務的向上權值，優先調度對工作流執行影響較大的任務，并且降低任務間通信代價，每次在為CCP分配VM時，綜合考慮對費用增長代價和截止期限的影響，因此有較高的調度成功率，在嚴格的截止期限內成功率均高于60%。

4.3.4 標準化執行成本

圖5中的實驗結果表明，工作流調度的成本通常隨著截止期限因子的增加而減少。由于NEC受調度成功率SR的影響，若無法找到合適的調度策略會引起數據值的缺失。在大多數情況下，CSACCP和RCT算法的性能優于IC-PCP算法，在所有工作流的截止期限內實現了最低的總執行成本。如所有啟發式算法一樣，有些方面表現并不是最優，但是這些方面都是少數。例如在Cybershake中，當α＜3時，RCT表現出更少的執行成本，但在此階段CSACCP比RCT有更高的調度成功率，且隨著截止期限因子的增加，CSACCP有著更好的表現。

Fig.5 Normalized schedule cost圖5 標準化執行成本

在Epigenomics工作流中，IC-PCP雖然在α＞3的階段內實現了更低的執行成本，但是該算法在大多數的截止期限內，無法滿足期限約束完成工作流的調度，尤其是在α足夠大的情況下調度成功率也只達到32%，而CSACCP則達到了100%。從圖5中可以看出，Montage和CyberShake在嚴格截止期限內調度產生的執行成本非常高，這是由工作流本身的結構所決定的。在截止期限非常嚴格時，工作流前兩層結構中的任務具有很高的并行度，任務需要并行執行，因此所有算法都需要租用更多的虛擬機實例來完成前期任務，這將導致更高的執行成本。

4.3.5 向上權值對算法性能的影響

CSACCP算法對HEFT中向上權值rank進行了改進，為了分析其對算法性能的影響，設定性能指標執行成本降低率CR（cost reduction rate），計算公式如下：

其中，NECH表示使用HEFT算法中rank的標準化執行成本，NECC表示使用CSACCP算法中ranku的標準化執行成本。

4種不同類型的大型工作流按截止期限因子遞增實驗結果如表4所示。

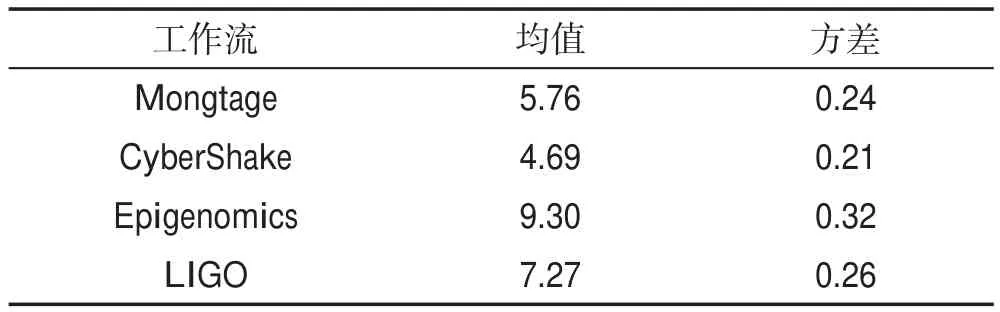
Table 4 Average execution cost reduction rate表4 平均執行成本降低率 %

表4中結果表明，對于大型科學工作流，優先調度出度高的任務，在滿足截止期限約束的前提下，可以有效降低工作流的執行成本，降低率均在4.6%以上。尤其是對于Epigenomics和LIGO工作流，降低率可達到7.2%以上，這與兩種工作流的結構特性有關。兩種工作流中都有大量的高出度任務，聚合任務的通信時間，提高任務的優先級，進一步縮短了工作流的執行時間，提高調度成功率。因此，CSACCP算法對向上權值進行改進，并為工作流設定約束關鍵路徑可有效降低執行成本。

總體來看，CSACCP在大多數情況下均可構造更優的調度方案，僅只在LIGO工作流的截止期限中RCT具有略高的調度成功率。在其他場景中，CSACCP均優于IC-PCP和RCT。

5 結束語

為了解決異構云環境下科學工作流截止期限約束的代價優化調度問題，提出一種基于約束關鍵路徑的代價優化算法CSACCP。算法綜合考慮云環境下資源異構性、數據通信開銷和虛擬機采集延遲等因素。算法對任務設定向上權值，并根據權值將工作流進行分解形成約束關鍵路徑CCP集合，整體分配CCP任務到最便宜實例，并且優先考慮回填策略，進一步提高資源利用率，降低執行代價。實驗結果表明，CSACCP算法不僅可以降低執行代價，還可以得到更高的任務調度成功率。在未來工作中，將考慮可靠性、能耗等QoS約束。另外，進一步結合云資源的付費模式，如Amazon的預留模式和Spot模式，提高本文工作流調度模型的適用性。