分層遞進的改進聚類蟻群算法解決TSP問題*

馮志雨，游曉明，劉 升

1.上海工程技術大學 電子電氣工程學院，上海 201620

2.上海工程技術大學 管理學院，上海 201620

1 引言

旅行商問題（traveling salesman problem，TSP）屬于NP難問題[1]，仿生進化思想的發展為NP難問題提供了新的思路，這其中以蟻群算法（ant colony optimization，ACO）最為顯著。蟻群算法的提出[2]，是源于Marco Dorigo的博士論文，它是一種具有進化思想的啟發式算法，根據正反饋機制實現種群間的信息交流。蟻群算法1992年提出至今，針對算法的不足，研究學者一直進行著改進工作以提高算法的實現效率。Dorigo等人[3]和Stützle等人[4]分別提出了蟻群系統、最大-最小蟻群算法，對傳統蟻群算法在信息素更新方式以及界限進行了改進；對于TSP問題，有n個節點，那么相應的就會有(n-1)!個可行解，對應的時間復雜度就變成了O(n!)。隨著TSP問題規模越來越大，時間復雜度會愈加增大，運算難度就會愈加增大。傳統蟻群算法在解決大規模的TSP問題時，運算時間會增大并且解精度會降低。因此，應對TSP問題，越來越多的學者試著結合多種智能算法的優點去獲得更好的運算性能。文獻[5]提出蟻群算法（ACO）與3Opt并行合作混合方法。利用蟻群算法找到TSP問題的路徑解，然后運用3Opt算法優化找到的路徑解，進一步提高解精度，避免算法陷入局部最優。雖然算法運行時間有所提高，但是為了算法中種群的并行運行，需要不止一臺實驗的仿真設備來完成，這無形中增大了仿真硬件要求。文獻[6]提出粒子群算法（particle swarm optimization，PSO）+蟻群算法（ACO）+3Opt方法，解決不同的TSP問題所需要的參數不盡相同，故利用粒子群算法去優化蟻群算法中的信息素因子α和啟發式因子β，以便蟻群算法可以找到期望的路徑最優解。然后再經3Opt算法優化解路徑。雖然算法提高了某些TSP問題的解精度，但是并沒有縮短算法的運算時間，并且當TSP問題規模增大的時候，提出的改進算法并沒有獲得較好的解路徑值。文獻[7]提出融合遺傳算法、模擬退火、蟻群算法、粒子群算法等多種群技術去解決TSP問題。先通過蟻群算法獲得初始最優路徑解，然后通過遺傳模擬退火算法去優化初始最優路徑，當迭代完成一段時間后，通過粒子群算法去優化各路徑上的信息素，然后再進行迭代運行。該算法在較大規模的TSP問題上獲得了理想的解路徑值，但是由于融合了多種優化算法，算法本身的計算復雜度被提高了，運算時間沒有縮短。文獻[8]提出了基于蟻群算法的改進信息素更新機制以及新的信息素平滑機制去解決TSP問題，利用迭代最優路徑上的信息素確定新探邊的動態最佳路徑變化信息，從而加快算法收斂速度，利用平滑機制對信息素矩陣進行重新初始化，從而擴大種群多樣性，增強算法的全局搜索能力，但是算法的計算復雜度為O(n2)，并沒有較大程度地降低算法的計算復雜度。

本文提出的DP-ACS（density peak clustering algorithm-ant colony system）算法利用分工合作[9]的思想，將大規模的TSP案例進行節點分組歸納，然后運用改進的蟻群算法尋找新形成的二類TSP問題的解路徑，最終切割斷點重組二類TSP問題的解路徑構成原始TSP問題的最優路徑。DP-ACS算法在保證問題解精度的前提下，明顯加快了算法運算時間，并且有效降低了算法的時間復雜度。

2 相關工作

2.1 TSP問題描述

旅行商問題是一個經典的組合優化問題，組合優化是根據數學方法對某離散事件進行整編、分組、排序等。旅行商問題是說一個旅行者要走遍給定數量的城市，但是前提這些給定的城市只允許旅行者拜訪一次，要求找出旅行者走遍每個城市后的最短路徑。給定的城市數量越大，求解問題的空間復雜度、時間復雜度不可避免地會增大，而且呈指數函數增長，因此TSP問題的解不是窮舉就可以得到的，問題的復雜度已經遠遠超出了人們想象。求解TSP問題的算法一般分為兩大類：精確算法和啟發式算法。前者適用于小規模旅行商問題，后者適用于中大型TSP問題。精確算法主要有定界法、規劃法等。啟發式算法有GA（genetic algorithm）、SA（simulated annealing）、PSO、ACO等。其中蟻群算法，由于具備進化思想，為解決旅行商問題提供了新的思路。

2.2 蟻群算法求解TSP問題

在標準的蟻群算法中，螞蟻根據式（1）[3]狀態轉移概率規則，判斷螞蟻下一個去往的城市。

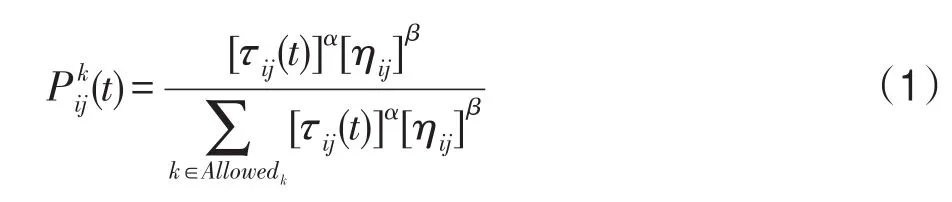
式中，τij(t)是t迭代過程中，城市i與j連接路徑上的信息素值；ηij是城市i與j連接路徑長度的倒數值，是一種啟發式信息，如果城市i與j連接路徑長度越短，那么螞蟻選擇的下一個城市越可能是j；Allowedk表示螞蟻k未走過的城市；α和β分別決定了信息素和啟發因子的重要性。當所有螞蟻完成了一次完整的路徑構建，即完成一次迭代，此時信息素的更新將會按照式（2）進行。

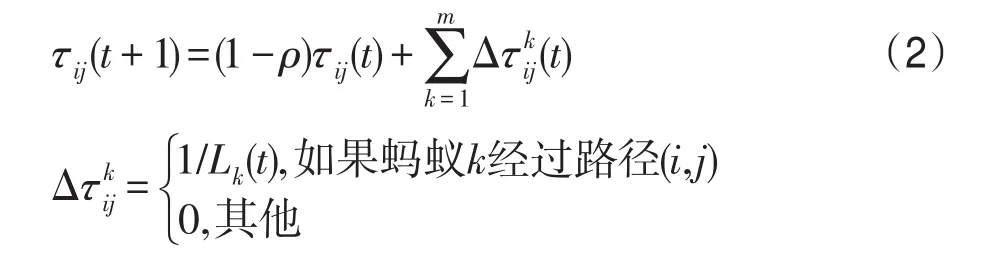
式中，ρ表示信息素揮發參數，m是每次迭代的螞蟻總數量，表示螞蟻k在路徑(i,j)上釋放的信息素值，Lk(t)是螞蟻k旅行路徑長度。通過設置最大迭代次數，當算法運行迭代數達到設定最大值，結束運行，得出算法最優解。如果在迭代過程中出現停滯現象，則初始化處理，從而擺脫停滯，繼續迭代運行，直到達到設定的迭代上界。

2.3 密度峰聚類算法

密度峰聚類算法（density peak clustering algorithm，DPCA）[10]的基本思想是對于一個數據集，聚類中心被一些低局部密度的數據點包圍，而且這些低局部密度的點距離其他有高局部密度的點的距離都比較大。DPCA主要有兩個需要計算的量：（1）局部密度ρi；（2）與高密度點之間的距離δi。密度峰聚類算法是將給出的數據點通過計算點與點之間的歐式距離dij，然后根據ρi以及δi選取出聚類中心，聚類中心的選取衡量標準是具備較大局部密度ρi和較大距離δi。然后將所有非聚類中心的散點歸類到比自身密度更大的最相近的類中心所在的簇中。

2.3.1 局部密度ρi

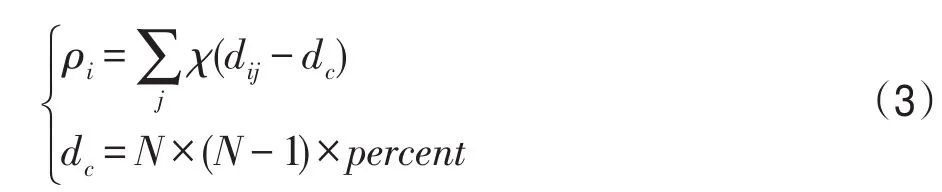
其中，dc是截斷距離，N是數據點總數，percent是比例因子，本文設為2%，ρi是統計數據點i與其他數據點的歐式距離小于dc的個數。

2.3.2 與高密度點之間的距離δi

式中，δi是在所有較數據點i的局部密度ρi都大的數據點中，選出那些點與數據點i的歐式距離的最小值。

2.4 3Opt算法

3Opt[11]是一個應用于優化旅行商問題解質量的局部搜索算法。在本算法中，3Opt主要用于從螞蟻找到全局最優解中任意挑選3對節點，打亂重新組合3對節點的連接，并記錄所有重新組合的8種連接情況。然后評估重新連接的線路質量與最初線路質量的好與差，如果比對出更好的連接線路，則覆蓋之前螞蟻找到的全局最優線路，反之保留起初線路。如果蟻群算法沒有使用3Opt，螞蟻容易陷入局部最小并導致搜尋不到最好的旅行長度，故3Opt進一步遏制了局部最優情況的發生。如圖1所示，左側連接圖有3條邊經3Opt算法處理后可以重新生成更優的連接圖。

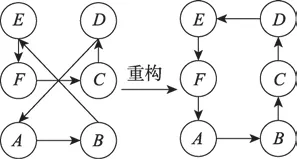
Fig.1 3Opt algorithm implementation圖1 3Opt算法實現

2.5 粒子群算法

粒子群算法[12]是一種基于社會環境的自適應算法，其中設置一組種群粒子去訪問給定域的盡可能的位置，每個位置都有對應的可計算的適應值。在每次迭代中，粒子將隨機地返回到先前的最佳適應位置和種群最佳適應位置。種群中的所有粒子都在分享自身找到的最佳搜索區域的信息。

粒子的運動由式（5）主導，vf表示粒子f的速度，xf表示粒子f的位置。

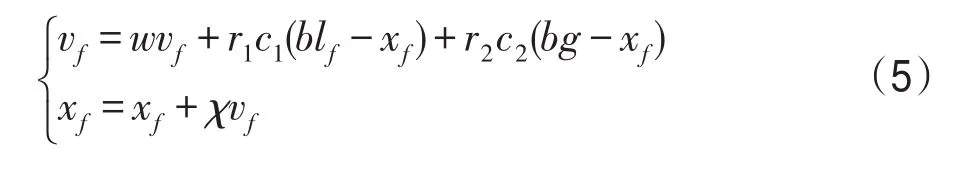
式中，c1、c2是非負整數，分別稱作“認知”與“社會”，前者是粒子本身的思考，后者是粒子間的信息共享與合作，都是學習因子。r1、r2是[0,1]內的隨機數，都是比例因子。w、χ是非負實數，分別稱作慣性權重和收縮因子。blf表示粒子f經過的歷史最好位置，bg表示種群中所有粒子所經過的最好位置。

3 改進算法（DP-ACS）

運用蟻群算法求解TSP問題的過程中，隨著TSP問題規模的增大，蟻群算法的運算復雜度會呈指數上升。當TSP問題中的節點數超過100時，依靠蟻群算法自身很難在運行時間和解精度之間找到平衡性，往往會消耗更多的時間去尋求更高的解精度。文獻[13]提出當TSP問題中的城市節點小于40個時，蟻群算法在運行時間以及求解的精度都獲得最優。文獻[14]提出了K-means聚類算法，這種算法快速、簡單，但是局限于處理數據分布呈球狀的簇。密度峰聚類算法是一種基于密度的聚類算法，尋求被低密度區域分離的高密度區域，能克服基于距離的算法只能發現“類圓形”的聚類的缺點，聚類形狀不受限制。

3.1 改進的密度峰聚類算法

密度峰聚類算法選取聚類中心依靠局部密度ρi和與高密度點之間的距離δi，故定義式（6）中γi為衡量點i是否為聚類中心：

因為聚類中心同時具備較大的ρi和δi，所以γi的值越大，說明點i越有可能是聚類中心，對集合γ進行降序排序，選取集合γ的前8%個點，記為DE（density），對排序后的點重新編號，記為j，然后繪制γ關于j的數據圖，數據圖呈非遞增狀態。

定義ε為拐點，點ε為數據圖中前后兩點的γ值相差過大的點，點ε滿足式（7）給出的條件：

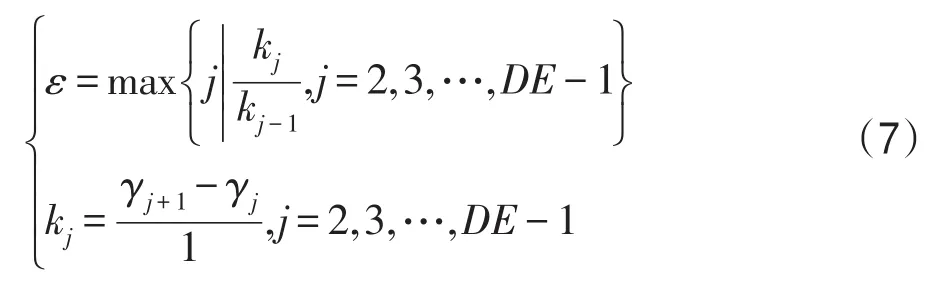
式中，kj表示點j+1與點j構成線段的斜率，當確定拐點之后，由于集合γ是降序排序的，故潛在的聚類中心點均位于拐點的左側。當確定了潛在聚類中心后，按照需要解決的TSP問題規模確定劃分多少個聚類中心。

如圖2，以TSP案例lin105為例，利用Matlab仿真繪制出γ關于j的排序圖，其中橫軸對應的是篩選出的城市節點重新編號，縱軸對應的是原城市節點根據式（6）計算的γ值，圖中數據點旁的標號是原TSP問題的城市編號。從圖2可以得出城市節點51是拐點，故城市節點77、23均為潛在的聚類中心。

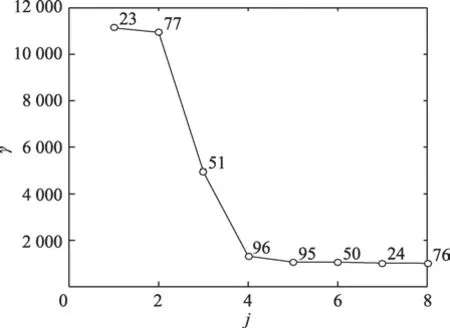
Fig.2 γsorting chart圖2 γ排序圖

3.2 改進的蟻群算法

文獻[2-4]的局部信息素更新都是根據式（8）進行的。

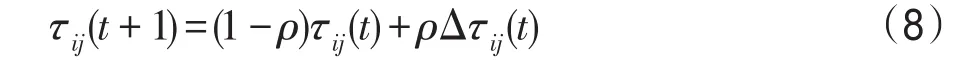
式中，ρ表示信息素揮發參數，取值范圍在[0,1]。一般將ρ的值設為0.1，但是TSP問題不同的數據規模算法需要的運算復雜度是不同的。ρ設為定值將不能滿足問題的解要求，比如kroA200，需要將ρ的值設大一些，以防蟻群算法過早收斂，獲得局部最優解，降低了算法精度。因此提出式（9）自適應地改變信息素揮發值。

其中，k為比例因子，設為0.1；c為歸一化因子，設為2。通過式（9）將信息素揮發參數ρ與信息素τij(t)之間建立線性關系。以e為底的指數函數呈單調遞增的特性，而信息素τij(t)的值隨著算法迭代運行呈上升趨勢。對τij(t)取反處理，這樣經exp函數處理后所得值控制在（0,1）內，從而經式（9）處理，信息素揮發參數ρ隨著信息素τij(t)的增大而增大，并且ρ的值控制在（0.1,0.2）。

算法迭代運行初期，TSP問題中節點構成的路徑上面螞蟻數隨機，信息素相差甚微，路徑與路徑間的受螞蟻的歡迎度相差不大。隨著算法的迭代運行推進，路徑上面的信息素量的差距開始拉大，此時某些受歡迎度高的路徑上的信息素值較高，這時在還沒有找到全局最優路徑的情況下，蟻群算法很容易陷入局部最優。這時根據式（9）的關系，避免了信息素過高帶來的影響，此時信息素揮發參數對應提高，有效遏制了較歡迎路徑上的信息素濃度的進一步提高。反過來，當信息素揮發參數ρ值升高時，必然會造成算法收斂速度的下降。這時候根據式（9）的關系，信息素τij(t)必然會略有提高來應對信息素揮發參數ρ值升高帶來路徑上面的信息素殘余量過少的情況，在一定程度上避免了蟻群算法收斂速度減緩的情況發生。信息素揮發參數ρ與信息素τij(t)之間相互平衡，當ρ過大時，τij(t)相應就會增大，避免算法運算復雜度的上升；當τij(t)過大時，ρ相應就會增大，避免算法過早收斂陷入局部最優。

3.3 改進算法的流程圖

本文DP-ACS算法求解旅行商問題的基本步驟如圖3所示。

由圖3可以看出，本文提出的改進算法（DPACS）先進行設置初始參數值，例如最大迭代次數、城市節點上信息素初始值、信息素揮發參數的初始值、螞蟻數量等，然后根據初始TSP問題數據集給定的節點坐標，運算節點與節點之間的歐式距離，進而根據式（3）截斷距離的定義計算dc，再根據式（3）、式（4）計算出每個節點的局部密度ρi以及與高密度點之間的距離δi。通過改進的密度峰聚類算法確定拐點，根據拐點的位置篩選出潛在的聚類中心，聚類中心的個數由初始TSP問題規模決定。根據選舉出的聚類中心形成簇，每個簇包含一個聚類中心，一個城市節點只能屬于一個簇。由于每個簇包含的節點數不盡相同，故利用粒子群算法去尋找對應不同規模的TSP問題應該設定的蟻群算法的信息素因子α和啟發式因子β。形成的這些簇中的數據節點各自又構成了新的TSP問題，本文稱為二類TSP問題。用具備自適應局部信息素更新的蟻群算法對二類TSP問題求解最優路徑解，當這些二類TSP問題結束運行后，通過近鄰原則選取兩個相鄰簇之間最近的兩個節點，切割斷開經過這兩個節點的相關路徑，通過之前斷開的節點之間的相互連接實現兩簇相連的效果，依此類推，將所有形成的二類TSP問題解路徑重新組合成全局解路徑，這樣二類TSP問題將還原成初始設置的TSP問題，解路徑從區域連接重新融合組成整體。再將重新連接后的全局路徑經過局部優化策略3Opt的處理，以達到進一步優化重新連接后的全局路徑的效果。最后通過算法辨別是否達到了預先設置的迭代次數上限。如果達到了，算法退出運行，輸出運行結果；否則，算法繼續迭代運行。如果算法在運行過程中出現停滯狀況，算法將進行初始化信息素操作，以達到強制算法恢復運行的效果。

Fig.3 DP-ACS algorithm flowchart圖3 DP-ACS算法流程圖

3.4 DP-ACS算法的原理圖

如圖4，以TSP問題lin105為例，改進算法先經過密度峰聚類算法處理，選取出3個聚類中心，分別是初始TSP問題的節點23、51、77，然后對新形成的二類TSP問題經改進的蟻群算法運算，找出各自的最優路徑解。由圖4可知新形成的二類TSP問題構造的是密閉的環形路徑解，需要通過近鄰原則選取節點進行分割。將左側的二類TSP問題的節點39與節點37之間的線段切割斷開，將右側的二類TSP問題的節點2與節點9之間的線段切割斷開，然后將左側的二類TSP問題的節點69與右側的二類TSP問題的節點1相連。因為TSP問題中規定每個被訪問的城市節點只允許訪問一次，考慮到構建的全局最優路徑解最短的要求，所以斷開右側的二類TSP問題的節點1與節點4之間連接的線段，然后將節點4與節點2相連。依此類推，斷開中間的二類TSP問題的節點2與節點18、節點3與節點4、節點19與節點22之間的線段，將左側的二類TSP問題中的節點37與中間的二類TSP問題的節點3相連，將右側的二類TSP問題的節點9與中間的二類TSP問題的節點22相連。同樣考慮到每個被訪問的節點僅允許訪問一次，將中間的二類TSP問題的節點2與節點4相連。最終經過改進的蟻群算法運算的所有二類TSP問題的局部最優路徑重組構成了初始TSP問題的全局最優路徑解，再經過3-Opt算法優化解路徑，最后得到了lin105問題的最優路徑解，即14 379。

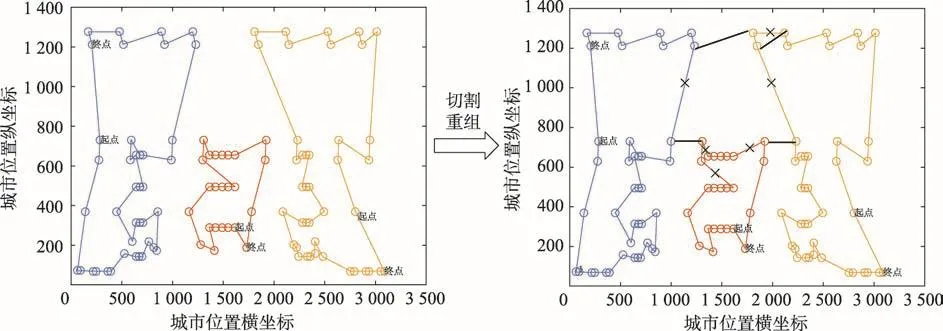
Fig.4 DP-ACS algorithm schematic圖4 DP-ACS算法原理圖

4 仿真實驗與結果分析

本文算法采用Matlab 2014b仿真軟件，基于Intel?CoreTMi5-4200M CPU@2.50 GHz處理器，RAM為16 GB，操作系統為64位的Win10。本文選取了TSPLIB里的典型問題集，這些問題集通常用于測試和優化算法。本文將問題集分為兩組進行實驗，一組是小規模，另一組是大規模。參考文獻[15]可知，密度峰聚類算法處理后的TSP問題形成的二類TSP問題規模在30～40個數據集節點最優。

如表1，利用粒子群算法中的粒子與種群尋找對應不同問題集的蟻群算法的信息素因子α和啟發式因子β。

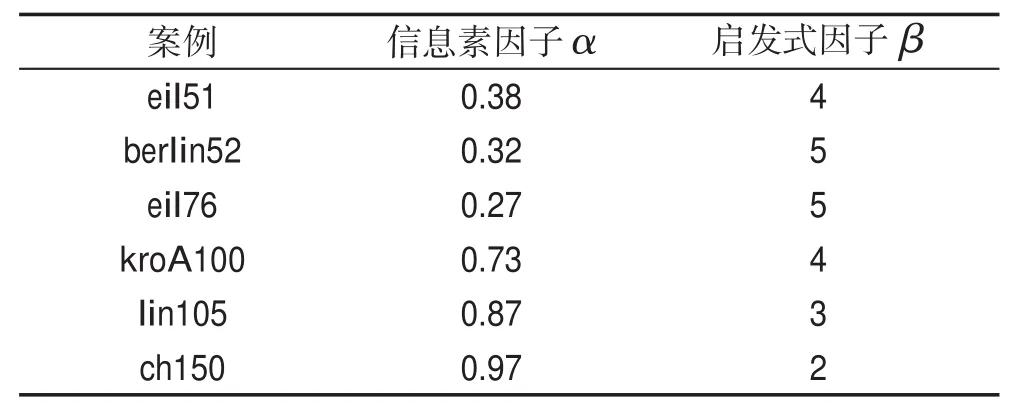
Table 1 Sets of parameters factor values表1 參數因子值集

如表2，設置蟻群算法的初始參數值以及算法運行迭代門限值等。

Table 2 Setting of basic parameters表2 基本參數設置

表2中ρ表示信息素揮發參數，Nmax表示算法運行迭代門限，Q表示螞蟻循環一周釋放的信息素總量，m表示螞蟻數，n表示城市節點數，τ0表示信息素初始參數值。

4.1 DP-ACS算法處理小規模TSP問題

圖5給出的是蟻群算法在迭代運行10次時，添加密度峰聚類算法和不添加密度峰聚類算法進行實驗比較。

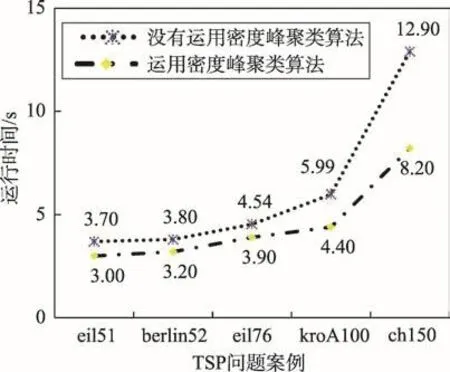
Fig.5 Comparison of algorithm running time圖5 算法運行時間對比

從圖5可以得出，經過密度峰聚類算法處理分割的TSP問題雖然在蟻群算法運算過程中還是需要一些時間，但是問題規模數據集節點的減少，降低了蟻群算法運算時間，并且運算時間減少會隨著問題規模的增大而越發明顯。當TSP案例的城市規模小于100時，算法之間的運行時間差距并不明顯，隨著城市規模增大，運用密度峰聚類算法所顯現出的優勢越發明顯。以kroA100問題為例，算法運行時間開始加快，比不使用密度峰聚類算法降低了1.59 s。以ch150問題為例，算法運行時間明顯加快，比不使用密度峰聚類算法降低了4.70 s。

如表3所示，選取6個規模不同的TSP問題案例，分別添加3Opt算法和不添加3Opt算法進行20次仿真運行，利用式（10）驗證3Opt算法對改進算法的運行時間和運行解精度的影響力。

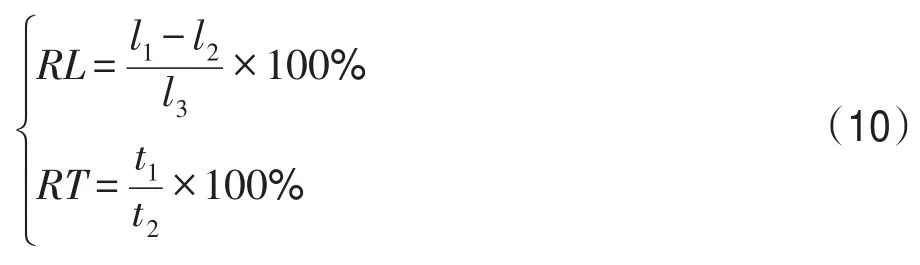
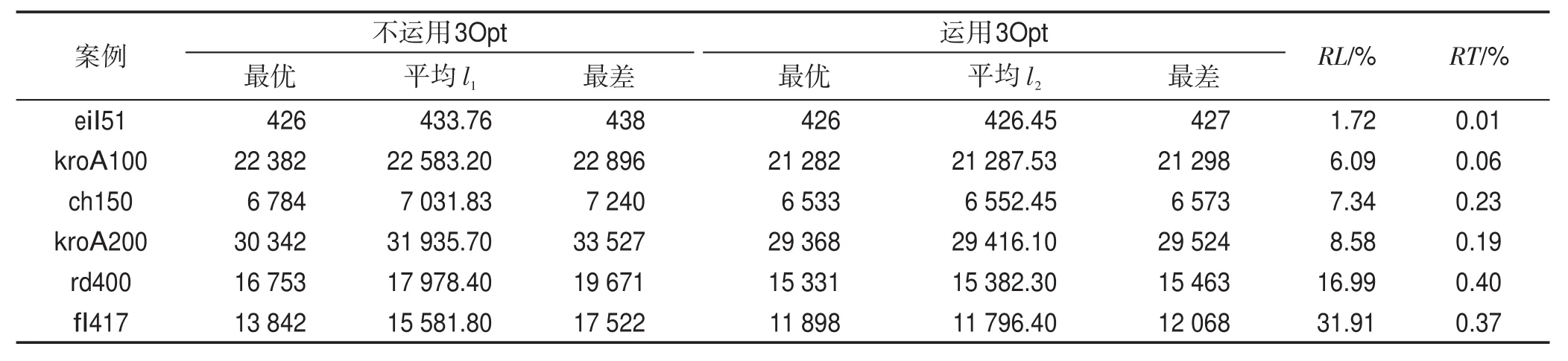
Table 3 Comparison of application of 3Opt algorithm表3 3Opt算法的運用比較

其中，RL表示路徑解相對優化比例，RT表示3Opt算法運行時間占改進算法的總運行時間比例，l1表示改進算法不運用3Opt算法的解長度平均值，l2表示改進算法運用3Opt算法處理后得到的解長度平均值，t1表示3Opt算法的運行時間，t2表示改進算法的總運行時間。

從表3中可以得出，選取的6個案例運用3Opt算法處理對改進算法找到的全局路徑解都起到了一定的優化作用，特別是案例fl417，路徑解相對優化比例達到了31.91%。雖然案例eil51優化力度最小，僅為1.72%，但是RT值最小，僅為0.01%，可以忽略不計。隨著案例規模的增大，運用3Opt算法處理顯現出的優勢越發明顯，并且RT值的增幅放緩。

從圖6可以得出，左側的全局路徑線路圖在未經過3Opt算法處理前，存在3處路徑線路重疊現象，右側的全局路徑線路圖在經過3Opt算法處理后，原先存在的3處重疊不存在了。因此經過3Opt算法的處理，可以將改進算法運算得出的全局路徑線路的邊緣重疊問題消除，減少路徑的總長度，從而得到更好的全局最優解。雖然3Opt算法提供了很好的路徑優化方案，但是運用3Opt算法增加了改進算法整體的運行時間，參考式（11）可以得出3Opt算法的時間復雜度為O(n3)。

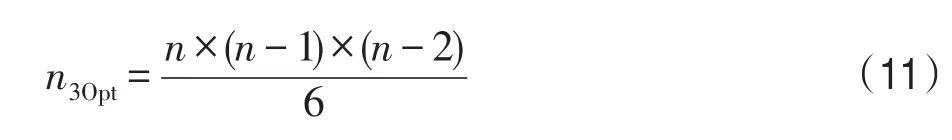
其中,n3Opt表示在3Opt算法中，需要檢查邊節點交換的次數，n表示城市節點數量。

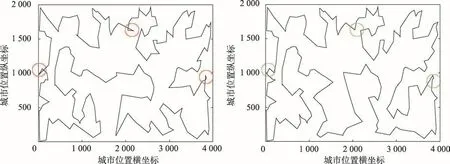
Fig.6 3Opt algorithm optimization case kroA200圖6 3Opt算法優化案例kroA200

為了讓改進算法加快解決TSP問題的時間，必須優化3Opt算法處理進程。3Opt算法是在重復地做著同一件事，比較三邊長短，然后新構造的邊短就會重新更新路徑，否則不會更改。因此通過加速這些單一步驟，整個改進算法的運行時間將會縮短。CPU并行方法是預先將節點與節點間的距離計算好存儲在緩存內存中，這種處理方法會隨著問題規模的增大而降低效率，并且也會受到內存帶寬的限制。故本文參考文獻[16]中的GPU并行方法，利用GPU內存存儲城市的坐標，并且存儲在共享內存的快速片上，需要時就計算兩城市間的距離，從而提高了數據讀取速率。隨著TSP問題規模的增大，GPU處理進程中計算兩城市間的距離的比例會降低，這是由于快速片具有共享性，并且相比于CPU并行方法，GPU并行方法具有更高的峰值內存吞吐量。

從表4可以得出，當TSP問題集選取案例較小時，比如eil51、berlin52，除蟻群算法外，DP-ACS算法與其他兩種算法的實驗結果相差不大，幾乎相同，并且算法均能找到eil51、berlin52問題的最優路徑解，解值分別是426、7 542。雖然說eil51和berlin52問題的城市點數幾乎相同，但是從它們的最優路徑解值可以看出它們各自的城市點位置分布稀疏情況不同，eil51的城市點與點之間更為靠近，berlin52的城市點與點之間更為疏遠。當通過改進的聚類算法對問題集berlin52進行聚類處理后，可以將問題中的城市點進行分類，劃分到一類簇中。然后根據粒子群算法優化后的參數α和β交由改進后的蟻群算法進行運算處理，這樣可以節約螞蟻判斷前往下一個城市的運算時間。因為由蟻群算法狀態轉移規則可知，兩個城市間的間隔越短，螞蟻從當前城市去往間隔短的城市的概率就會越大，密度峰聚類就是把離中心節點最近的城市化為一類，那么在這一類中的節點與節點之間的距離遠遠小于與其他類中的節點距離。

本文選取5組小規模TSP問題集，即eil51、berlin52、eil76、kroA100、ch150，用改進算法進行仿真實驗，每組TSP問題分別實驗20次，并將DP-ACS算法的實驗結果與 ACO[17]、ACO+3Opt[5]、PSO+ACO+3Opt[6]進行比較。蟻群算法中參數α與β值的選取參考表1中的6個小規模TSP問題對應的參數值設置。

從表4可以得出，針對eil51問題，DP-ACS算法在找到問題最優路徑解值的前提下，標準差較ACO[17]降低了3.72，這說明DP-ACS算法更加穩定，實驗仿真結果的波動性更小。針對kroA100問題，DP-ACS算法與其他算法相比，平均值分別降低了1 581.66、28.34、146.64。DP-ACS算法在20次仿真實驗中得出的最優路徑解值更接近問題已知最優解，因此DPACS算法的解精度更高一些，并且較ACO[17]、PSO+ACO+3Opt[6]，DP-ACS算法可以找到問題已知最優路徑規劃。在標準差值中，DP-ACS算法比其他算法低211.73、10.27、54.79，得出DP-ACS算法具有更高的穩定性，算法每次找到的最優路徑解偏差較小，改進算法具有更強的魯棒性能。針對ch150問題，DPACS算法找出的最優路徑解與已知最優解值相差只為5，與已知路徑最優解值幾乎相同，比ACO[17]找到的路徑最優解縮小了115.51，比ACO+3Opt[5]找到的路徑最優解縮小了37，比PSO+ACO+3Opt[6]找到的路徑最優解縮小了5，DP-ACS算法較大程度上提高了算法的解精度，改進算法在平均值和標準差上都比其他算法更優，故DP-ACS算法具有更強的穩定性。

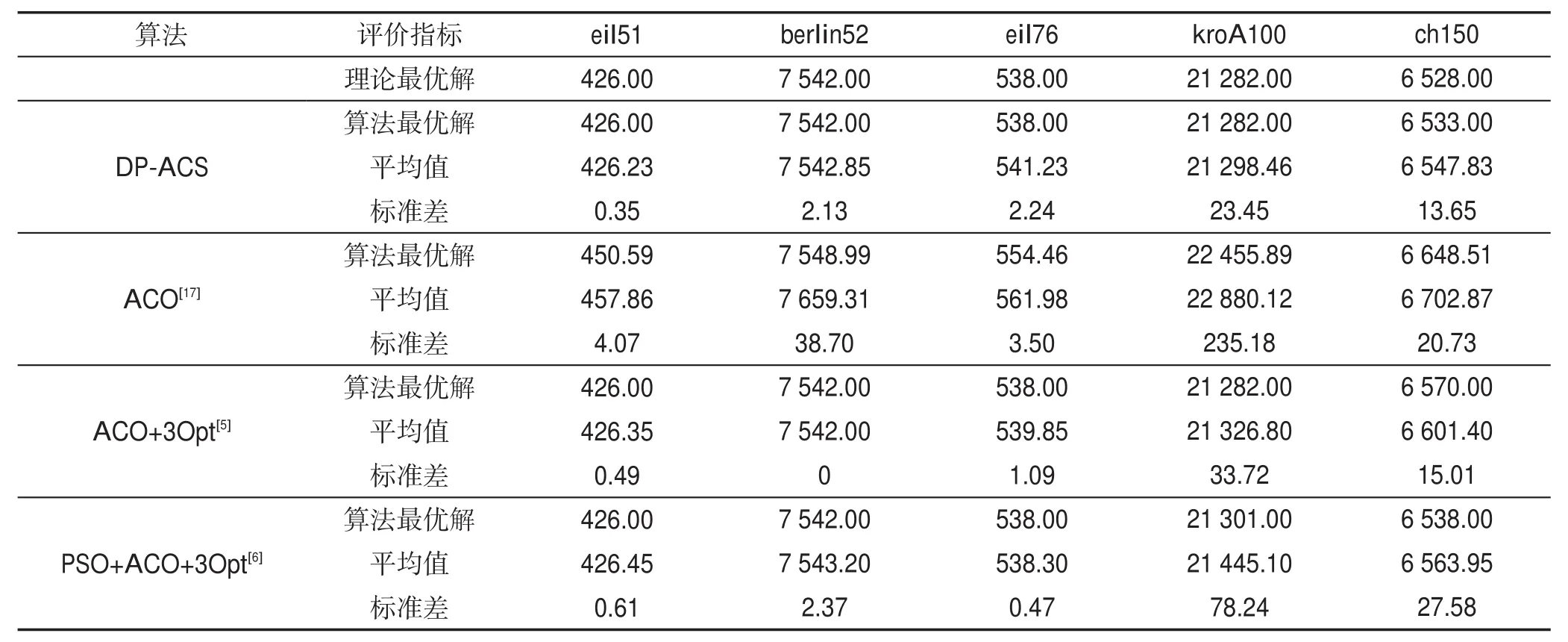
Table 4 Comparison of DP-ACS algorithm with other algorithms on small-scale TSP instances表4 DP-ACS算法與其他算法在小規模TSP案例上的比較

4.2 DP-ACS算法處理大規模TSP問題

本文選取4組大規模TSP問題集，即kroA200、rd400、fl417、d493，用DP-ACS算法進行仿真實驗，每組TSP問題分別實驗20次，并將DP-ACS算法的實驗結果與 ACO+3Opt[5]、PSO+ACO+3Opt[6]進行比較。ACO中參數α與β值的選取參考表1中的TSP問題對應的參數值設置。

對于大規模的TSP問題，通過密度峰聚類算法處理后得到的簇中包含的數據集節點限制在40個以內[15]。然后經過蟻群算法運算后各自形成的二類TSP問題的路徑圖，這些簇與簇之間交流的時間很短，通過找到兩個聚類簇之間最近鄰節點，然后切割重組成初始TSP問題的最優路徑圖。對于大規模的TSP問題，運用密度峰聚類算法和不運用密度峰聚類算法之間的差別是顯著的，特別在算法運行時間上的減少是明顯的。

由表5可以得出，與ACO+3Opt[5]、PSO+ACO+3Opt[6]相比，DP-ACS算法找到了案例kroA200的最優路徑解，并且在平均誤差百分比（平均值與理論最優解的差值除以理論最優解）上降低了0.7%，因此DP-ACS算法運行更加穩定。在案例rd400、fl417上，DP-ACS算法的平均誤差百分比分別降低了1.28%、1.79%、0.66%、0.6%，DP-ACS算法在每個TSP案例中的20次仿真實驗結果精度更高，解路徑值更加接近TSP案例的理論最優解。在案例d493上，DP-ACS算法的運算結果精度有所提高，較其他算法的最優解值，DP-ACS算法找到的最優路徑分別縮短了382、436。

對于大規模的TSP問題，經過改進的密度峰聚類算法處理后，得到的二類TSP問題城市節點數量較初始TSP問題更少，這樣減輕了具備自適應信息素更新機制的蟻群算法的運算復雜度。相對于大規模TSP問題，蟻群算法解決二類TSP問題更容易找到全局路徑最優解，對于螞蟻在尋找自身的局部最優解的時候，城市節點數量越少，蟻群更加容易找到局部最優路徑，密度峰聚類算法的運用加快了蟻群算法在處理二類TSP問題的收斂速度，并且由于城市數量的減少，蟻群算法[18]不易陷入局部最優。當全局路徑線路經過3Opt算法處理后，進一步優化算法已知最優路徑解，有效地提高了解精度，本文在構建局部最優路徑路線的基礎上優化了全局最優路徑路線。

4.3 算法收斂速度與多樣性分析

選取4個TSP問題的基本案例，kroA100、ch150、kroA200、fl417，將 DP-ACS算法與蟻群算法（ant colony system，ACS）、最大-最小蟻群算法（max-min ant system，MMAS）進行仿真實驗對比。

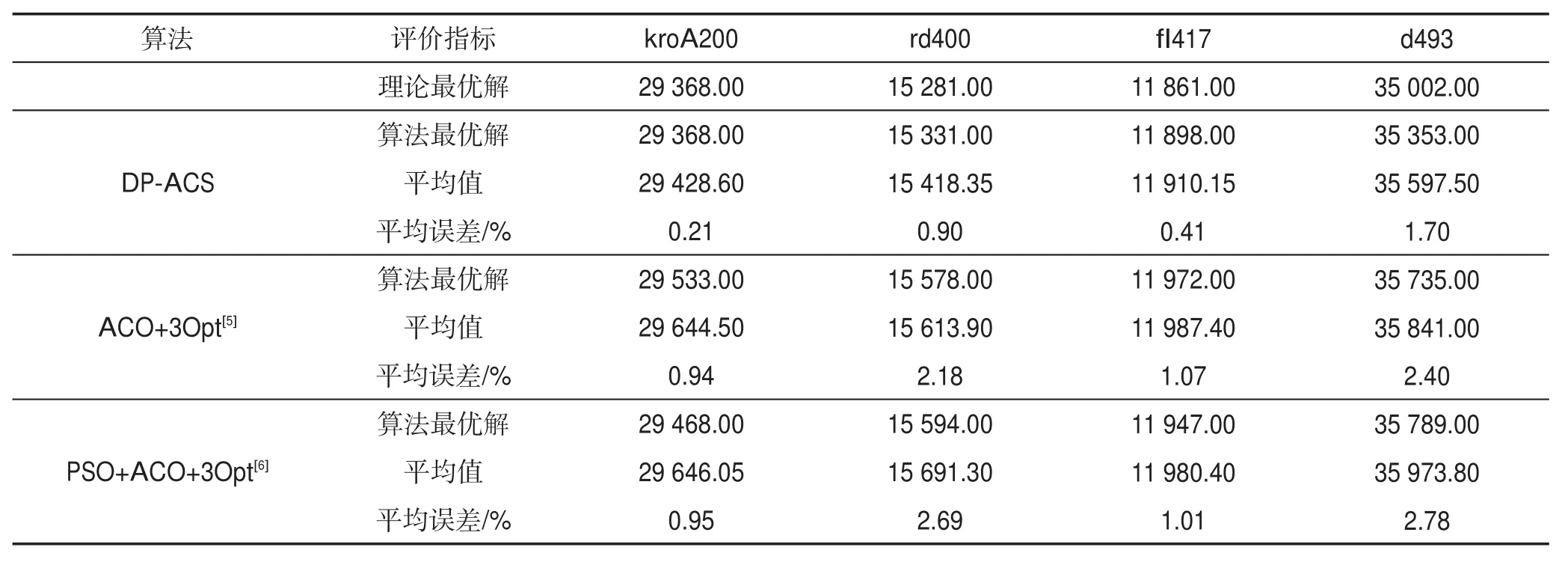
Table 5 Comparison of DP-ACS algorithm with other algorithms on large-scale TSP instances表5 DP-ACS算法與其他算法在大規模TSP案例上的比較

從圖7（a）可以得出，DP-ACS算法在kroA100案例中收斂速度比ACS算法、MMAS算法都快，大約在算法迭代運行了500次后，DP-ACS算法已經收斂到了全局最優解，即21 282。雖然ACS算法多樣性很強，但是ACS算法并沒有找到全局最優解。從圖7（b）可以得出，DP-ACS算法在前180次迭代運行中，路徑解都在不斷經過優化，并且從迭代曲線看，每次迭代優化的數值都較大。而ACS算法自80次迭代運行開始就收斂到了算法找到的最優解，陷入了局部最優，解路徑值沒有再變優。MMAS算法表現出豐富的多樣性，但是找到的路徑最優解較DP-ACS算法還是相差甚遠。從圖7（c）可以得出，DP-ACS算法表現出的全局多樣性更優越，ACS算法收斂速度慢并且算法找到的結果與理論最優解相距甚遠。MMAS算法過早收斂到算法最優解，多樣性較差，并沒有找到理論最優解。從圖7（d）可以得出，當所選TSP案例增大時，DP-ACS較其他算法更加優越，種群多樣性更優，沒有出現過早收斂的情況，而ACS算法、MMAS算法均在300次迭代后陷入局部最優，并沒有有效提高算法的解精度。

圖8（a）、圖8（b）分別是ACS算法與DP-ACS算法在解決fl417問題所表現出的算法多樣性[19]。從圖8（a）可以得出，ACS算法在前200次迭代運行中，前后迭代運算的標準差呈上升趨勢，種群多樣性較好。但是圖8（b）中DP-ACS算法所表現出種群多樣性更好，DP-ACS算法在前700次迭代運行過程中，前后迭代運算的標準差一直呈上升趨勢，這說明DPACS算法一直在不斷優化解路徑。對比圖8（a）和圖8（b），DP-ACS算法每次迭代運算的標準差都較ACS算法的標準差數值大，在第400次迭代時，DP-ACS算法運算出的標準差數值較ACS算法運算出的標準差相差約500，這表明了DP-ACS算法中每次迭代運行中的螞蟻所尋找的路徑解數值相距較大，DP-ACS算法表現出更好的種群多樣性。

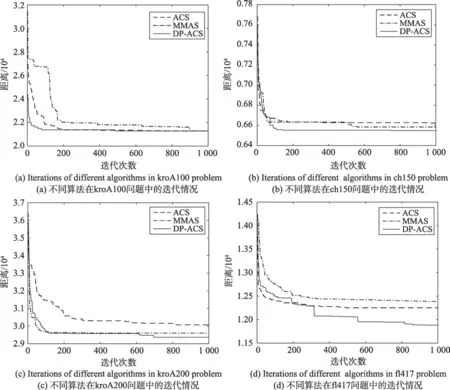
Fig.7 Comparison of algorithm iterations for different TSP problems圖7 不同TSP問題的算法迭代情況比較

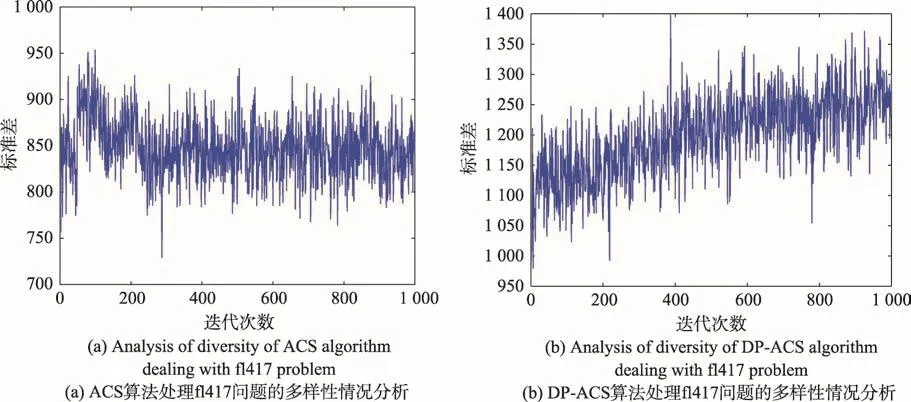
Fig.8 Comparison of algorithm diversity圖8 算法多樣性比較

4.4 分析時間復雜度

如表6所示，選取6個TSP問題案例，然后經過改進算法的運算，統計20次仿真實驗，求取平均運算時間，比較改進算法與ACO+3Opt[5]算法、PSO+ACO+kOpt[20]的平均運算時間。

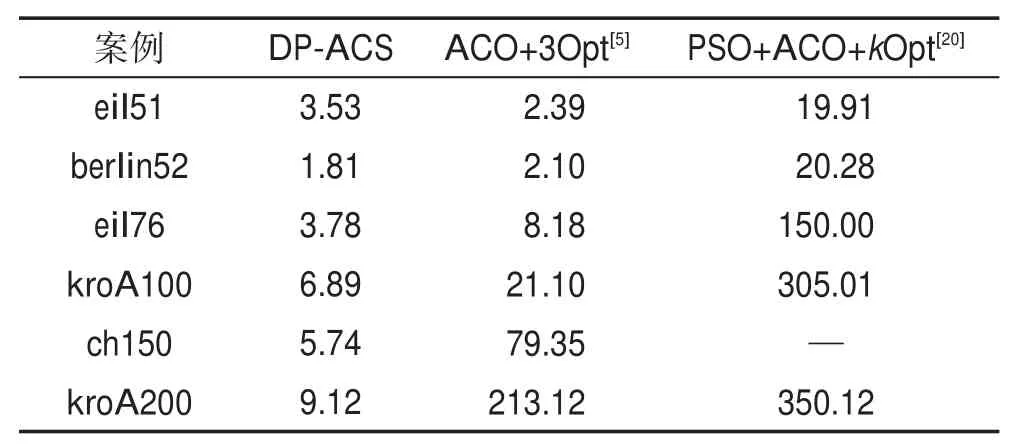
Table 6 Comparison of running time between improved algorithm and other algorithms表6 改進算法與其他算法的運行時間比較 s

從表6可以得出，隨著案例的城市節點數量上升，3種算法的運算時間均在增大。由于ACO+3Opt[5]算法沒有經過聚類[21-22]處理以及沒有運用粒子群算法，因此針對eil51案例，ACO+3Opt[5]算法運算時間更短。但是，隨著案例規模的增大，改進算法的運算時間顯現出明顯的優勢。

DP-ACS算法的運行時間是衡量算法優化TSP問題性能的一個重要指標。對于單純用蟻群算法解決TSP問題，提出式（12）來表達算法的運算復雜度。

其中，Nmax是蟻群算法迭代運行的次數，n表示TSP問題規模，即城市節點總數額，c表示與n成比例的常數。

令nm表示TSP問題經過密度峰聚類算法聚類形成的二類TSP問題所能包含的最大節點數額。本文參考文獻[14]將nm設置為40。提出式（13）來計算DP-ACS算法的時間復雜度。

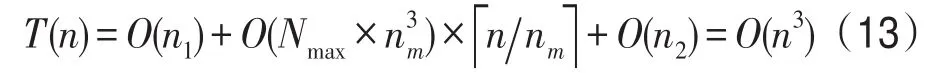
其中，O(n1)是密度峰聚類算法對TSP問題每個節點進行計算處理的時間復雜度，O(n2)是經過3Opt算法進一步優化找到的最優路徑的時間復雜度O(n3)。因為經過密度峰聚類算法處理過的TSP問題形成的二類TSP問題規模大致相同，并且每個二類TSP問題的規模都不會超過nm，所以蟻群算法處理二類TSP問題的時間復雜度為然后再乘以經過向上取整的n/nm，得出經過密度峰聚類算法處理后的蟻群算法時間復雜度O(n)，其中表示聚類算法處理后形成的二類TSP問題的數額。因此，整個改進算法的時間復雜度為O(n3)。

4.5 DP-ACS算法找到的最優路徑圖

如圖9～圖12，分別是DP-ACS算法就TSP問題ch150、lin105、kroA200、fl417處理得到的算法最優路徑解。

Fig.9 Optimal path for ch150 problem(length:6 533)圖9 ch150問題的最優路徑(最短距離:6 533)

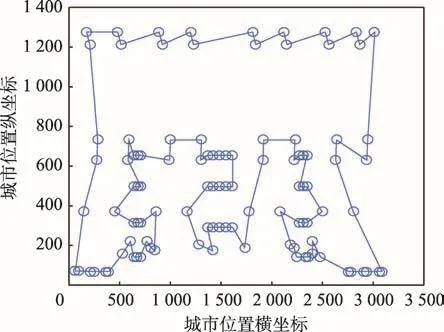
Fig.10 Optimal path for lin105 problem(length:14 379)圖10 lin105問題的最優路徑(最短距離:14 379)

5 結束語

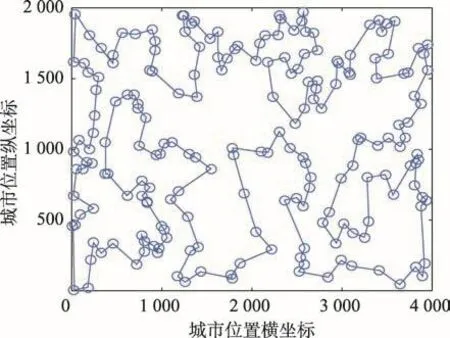
Fig.11 Optimal path for kroA200 problem(length:29 368)圖11 kroA200問題的最優路徑(最短距離:29 368)

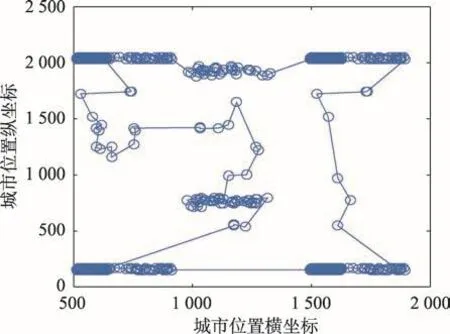
Fig.12 Optimal path for fl417 problem(length:11 898)圖12 fl417問題的最優路徑(最短距離:11 898)

隨著TSP問題規模的增大，蟻群算法在問題解精度以及算法收斂速度上表現不足[23]，提出具有自適應信息素更新策略的聚類蟻群算法（DP-ACS）。利用密度峰聚類算法將原始TSP問題切割成較小的簇，這些簇再由具有自適應信息素更新策略的蟻群算法求解形成解路徑。這些二類TSP問題各自形成的閉合解路徑通過近鄰點切割斷開重組構成原始TSP問題的解路徑回路，再經局部優化策略（3Opt）優化最優路徑解，通過這些改進策略共同作用提高改進算法的性能。實驗結果證明，DP-ACS算法的最優解精度以及收斂速度都較其他的改進蟻群算法更優越，當TSP問題規模增大的時候，DP-ACS算法的優越性更加突出。在接下來的研究過程中，將探討蟻群算法求解二類TSP問題的解精度與算法的迭代運行次數之間的關聯；另一方面，將研究二類TSP問題各自形成的解路徑如何有效地連接在一起構成全局最優路徑。