一種基于改進型EMD的一維雷達距離像信號分析

程占昕 王艷娜

（1.海軍大連艦艇學院信息系統系 大連 116018）（2.92677部隊 大連 116018）

1 引言

一維雷達距離像是雷達目標識別領域的熱點和難點問題。在距離像分析中，用什么樣的特征來表達目標屬性是至關重要的，高分辨距離像的特征提取和特征選擇是雷達目標識別的關鍵環節［1～2］。一維雷達距離像根據散射點模型理論，散射點在距離單元分布可分為三種典型情況：1）距離單元內分布眾多強度相當的小散射點，沒有明顯的特顯點，這類單元的回波起伏比較小，比較穩定；2）距離單元內只包含一個特顯點和眾多強度弱得多的雜散射點，這類單元的回波幅度基本由特顯點確定，眾多弱散射點使回波幅度起伏較小，因此，這類單元回波也比較穩定；3）距離單元內包含少數幾個，特別是2、3個特顯點，同時也會產生較多弱散射點，當目標相對雷達轉動時，特顯點回波的差拍作用使引起這類距離單元回波幅度有大的起伏，特顯點橫距差越大，起伏越快，因此，這類單元的回波幅度隨目標姿態變化起伏通常很大［3］。

與很多關于樣本特征提取和特征選擇方法的研究不同，本文試圖從時頻分析的角度對一維雷達距離像進行分析，通過分量分解以及對應的Hilbert-Huang時頻譜對距離像進行一定的特征分析和探討，力爭能夠從Hilbert-Huang的角度對這一領域進行嘗試探討。

2 傳統的EMD分解概述

EMD的基本模式分量，稱內蘊模式函數（IMF），也可看作類小波擴展［4～5］其滿足如下條件：

1）整個數據序列的極值點與過零點的數量相等，或至多相差一個。

2）任一時刻，由極大值和極小值定義的信號包絡均值為零。

按過零點定義信號的周期，即一個周期只包含一次基本模式的振蕩，不存在復雜的疊加波，因此，IMF不限定于窄帶信號，可以是幅度或頻率調制信號，也可以是非平穩信號。EMD的IMF分量Hilbert變換后進行時頻分析，因此EMD分解+Hilbert變換統稱為Hilbert-Huang變換［6］。

對各分量進行Hilbert變換，獲取時頻分析，稱之為Hilbert-Huang時頻譜［7］，如圖1所示。通過下面公式求瞬時頻率：

其中，z(t)是實信號 f(t)=a(t)cos[φ ( t)]的解析信號，其a(t)為IMF的瞬時幅度。由于微分法對噪聲很敏感，可采用trapezoidal積分算法估計IMF的瞬時頻率［8］。由圖1可見，Hilbert-Huang時頻譜具有很高的時頻聚集性，沒有交叉項，優于Wigner-Ville時頻分析。

對于雷達距離像，不僅特顯點幅度變化劇烈，相位以及頻率等也錯綜復雜，而且還存在一維空間相關性。因此，EMD必須解決如下問題：

1）選取最優插值函數。目前，常用的插值函數包括徑向基函數、樣條插值、三次插值以及三角幾何插值等。對于同一雷達距離像，采用不同的插值函數可能會得到不同的分解結果。

2）確定待插值極值點。對于一些極值點的特殊分布情況，如大寬度特顯點，甚至沒有或極度缺乏的極值點時，幾乎所有的已有EMD方法均失效。

本文提出一種噪聲輔助的EMD雷達距離像特征分析與提取方法。根據白噪聲在EMD下的分解特性，把白噪聲加入到信號中來補充一些缺失的尺度，進而達到更好的分解結果。

3 基于噪聲輔助信號分析的改進型EMD分解

依據零均值白噪聲的特性，本文提出了一種新的噪聲輔助信號分析方法，定義如下：

1）在原信號 f(t)的基礎上加上具有相同方差的隨機零均值高斯白噪聲信號nj(t)（其中j=1，2，…，J），得到輔助信號：

圖1 兩個單分量信號的EMD分解及Hilbert-Huang時頻分析

2）在原信號 f(t)的基礎上減去1）中的零均值高斯白噪聲信號 nj(t)（其中 j=1，2，…，J），得到輔助信號：

3）分別對上式中得到的輔助信號 fn(j+)(t)和fn(j-)(t)進行經驗模式分解：

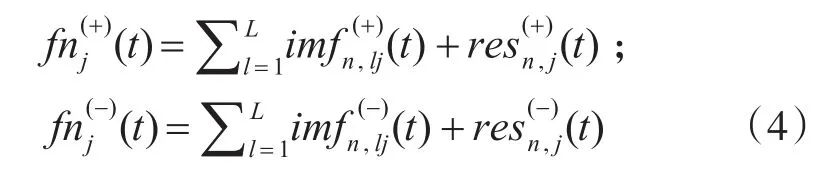
4）均值：

5）得到IMFs和剩余量：

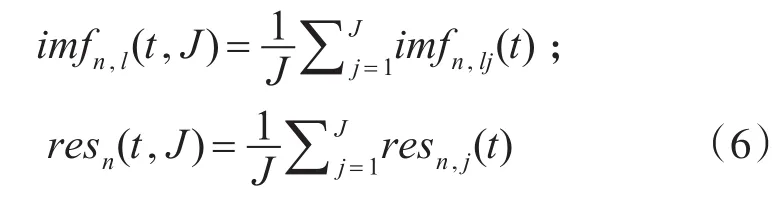
6）得到：

最后，應用式ωi()t=對每個分量進行瞬時頻率求解以及對應的時頻譜分析。

4 基于改進型EMD的距離像性能分析

傳統EMD的缺陷嚴重地影響了算法性能和結果。本文根據傳統EMD的缺陷，提出了上述改進型EMD算法，并應用到一維雷達距離分析中去。其中主要的問題主要包括以下幾方面。

4.1 IMF分量對方位敏感性分析及抑制

經驗模式分解對于極值點分布比較敏感，這一點毋庸置疑，但是，同時考慮到散射點不發生MTRC的方位角范圍內，目標的散射點模型基本不變［9～10］。因此，為了抑制IMF分量對方位敏感性，我們提出了分數階相位平移下的Hilbert變換對應的分解方法：即首先把信號進行Hilbert變換獲取90°相移后的信號；第二，應用分數階角度的概念把Hilbert變換獲取90°相移后的信號進行任意角度的相移，這樣就可以獲取0°～360°范圍內任意相移下的信號。第三，對這些不同相移后的信號進行經驗模式分解，然后進行反向相移。最后，把所有獲取的結果進行加權求平均，即為最終結果。該方法可以有效地抑制方位敏感性，獲得可靠的結果。多次試驗結果證實，10到20次相移后的結果可以獲取較好的效果，同時又不會增加過多計算量。

4.2 IMF分量對平移敏感性分析

經驗模式分解對于極值點分布比較敏感，這一點導致了IMF分量對平移的敏感性。但是，只要各個極值點相對位置不變，IMF也就保留了穩定的特性，只要把IMF分量進行相應的逆向平移對準，所有的平移問題就可以解決［11］。

這個問題相對簡單。一般來說，在進行經驗模式分解前我們就可以把平移問題解決，這樣經驗模式分解對于平移敏感性問題就可以不用考慮。

4.3 IMF分量對強度敏感性分析

正如前述，經驗模式分解最為敏感的問題是極值點分布位置（包括相對位置）以及極值點個數等等。各個IMF分量的強度大小的變化如果不足以改變極值點個數和相對位置，那么這種變化對于經驗模式分解來說就不會產生IMF分量變化的敏感性（當然除了強度外）。

這一點正好與一維雷達距離像的局部能量波動相對應。很多情況下，由于各種原因，一維雷達距離像中的各個分量只是能量產生了小的波動，這種波動既沒有改變主要極值點個數，也沒有改變極值點相對位置，因此通過經驗模式分解，IMF分量個數不會產生大變化，同時每個IMF分量對應的頻率也幾乎不會產生變化［12］。結果是，小的能量波動不會產生頻率和個數的變化。因此，這一特性說明了在一定量的強度變化范圍內，IMF沒有強度敏感性。

4.4 新特征量的定義和選取

基于4.3的分析，我們可以得出結論，采用Hilbert-Huang時頻譜作為特征分析不失為一種選擇。但是，采用Hilbert-Huang時頻譜只能夠提供各個分量瞬時頻率和瞬時能量的分布，因此，為了進一步有效應用各個分量的瞬時頻率與瞬時能量，這里我們提出另外一個指標和Hilbert-Huang時頻譜一道使用，平均瞬時頻率，定義為

其中，L為IMF分量個數。

平均瞬時頻率/能量比具有以下特性：

1）可以反應出信號的主要頻率分布

假定這里只有兩個IMF分量，且ωimf1(t)=100，imf1(t)=cost，ωimf2(t)=1，imf2(t)=sint，則可以得到：

也就是說，信號的主要頻率是ωimf1(t)=100，幾乎可以把ωimf2(t)=1忽略不計。

2）可以獲得特顯點發生的主要時刻

特顯點具有特別強的能量，因此，通過平均瞬時頻率的求解，可以近似獲取特顯點對應的時刻。這種特顯點的時刻估計與時域內的估計方法相比由于通過平均意義的算術運算獲得的，因而具有更強的魯棒性。同時，也告訴我們，特顯點除了在時域內估計外，還可以通過時頻分析進行估計。這種方法補充了特顯點的估計方法，充實了特征提取的內容，增加了工程可靠性。

3）可以獲得主要特顯點發生的個數

由于特顯點具有特別強的能量，因此，每一個特顯點必然對應一個大的凹點或者凸點，通過對這種變化劇烈的凹凸點進行統計，就會近似獲取特顯點的個數。這種特顯點的個數估計與時域內的估計方法相比由于通過平均意義的算術運算獲得的，因而同樣具有較強的魯棒性。同時，特顯點個數除了在時域內估計外，還可以通過時頻分析進行估計。這種方法補充了特顯點的個數估計方法，充實了特征提取的內容，同樣會增加工程的可靠性。

5 結語

本文提出了一種改進型EMD分解算法并把其應用于一維雷達距離像的數據分析中。改進型EMD分解算法克服了傳統EMD分解算法的一些主要缺陷，可以更好地對非線性、時變信號進行分析。結合一維雷達距離像的特點，提出了平均瞬時頻率和Hilbert-Huang時頻譜結合應用的試驗分析，該種方法在一維雷達距離像分析中具有重大的潛力。