大girth多進制陣列準循環LDPC碼

劉 冰 任席闖 崔 潔

（中國人民解放軍91469部隊 北京 100841）

1 引言

1998年，Davey和Mackay重新發現了多進制LDPC（Low-DensityParity-Check）碼［1］，并提出了用于譯碼的多進制和積算法（Q-arySum-ProductAlgorithm，QSPA），相比于二進制LDPC碼來說取得了明顯的編碼增益，多進制LDPC碼的出現為LDPC碼的研究開拓了一個新的領域，也有許多關鍵問題亟待進一步研究。多進制LDPC碼除了具備二進制LDPC碼的一般特性外，還具有獨特的優勢，如當碼長較短時具有更好的糾錯能力，更強的抗突發錯誤能力，且適合高速率傳輸系統。

Tanner圖中環的大小和分布是影響多進制LDPC碼性能的重要因素之一，特別是短環的存在會破壞變量節點和校驗節點信息傳遞的獨立性假設，使相關信息在兩類節點之間傳遞，影響碼字的迭代收斂過程，造成譯碼性能急劇下降。一般構造碼字之初就會考慮消除4環，而且此類研究成果已經非常豐富［2～5］。Tanner圖中最短環的長度稱之為 girth（圍長）。小girth（最小環）會對低碼率、長度較短的碼字影響較大，消除這類碼的短環或減少其分布可以帶來明顯的性能改善。另一方面，Tanner圖的girth還與碼的最小距離有關，一般girth越大，最小距離也將隨之增大，但最小距離并不隨girth增大而無限增大，一味地增大girth并不能提高碼字的性能［6］。因此，構造大girth（girth≥8）的多進制LDPC碼是多進制LDPC碼的一個研究方向。

對于迭代譯碼的準循環（Quasi-Cyclic，QC）LDPC碼來說，短環的存在不利于算法的收斂，性能損失的一部分原因歸咎于小girth的存在。目前，大多數構造方法都考慮了消除4環，即girth至少為6。構造出girth為8，甚至更大girth且具備低復雜度的多進制QCLDPC碼是當前的研究熱點之一［7～10］。構造大girth的主要方法有直接構造法和短環刪除法，其中直接構造法是根據設計的規則使得校驗矩陣達到大girth的特性。本文從大girth指數矩陣出發，提出了在不同域上廣義多進制位置向量和廣義二維擴展方法，采用直接構造法確定短環線性約束方程，與大girth陣列碼結合構造出了大girth多進制陣列LDPC碼。

2 大girth多進制準循環LDPC碼

2.1 大girth指數矩陣構造

陣列碼是一種準循環的LDPC碼，其校驗矩陣是由許多個的循環置換矩陣陣列所組成，形式為

其中，P是大小為 p×p的循環置換陣，p為素數，陣列行序號 a0，a1，…，ar-1是取值范圍為 [0，p-1]的不同整數。H的指數矩陣定義為

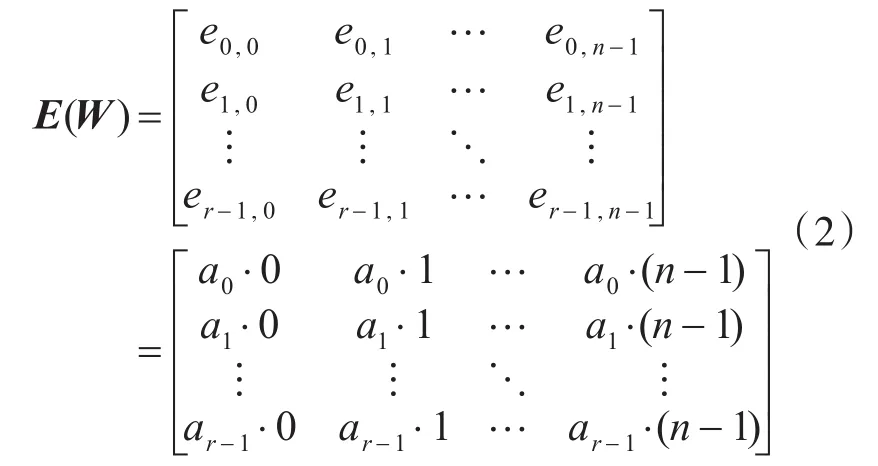
其中，ei，j=ai·j，0≤i≤r-1，0≤j≤n-1，W 表示校驗矩陣H 的基矩陣。如果序列a0，a1，…，ar-1形成 等 差 數 列 ，即 對 于 i=0，1，…，r-2 ，ai+1-ai=d≠0，稱對應的碼為等差陣列碼。如序列a0，a1，…，ar-1未形成等差數列，則稱之為非等差數列碼。

校驗矩陣girth的控制主要放在指數矩陣層面上。任何奇偶校驗矩陣H中長度為2i的閉環可形成陣列行和陣列列的序號對(r0，n0)，(r0，n1)，(r1，n1)，(r1，n2)， …，(ri-1，n0) ， 其 中 ，rk≠rk+1，nk≠nk+1，ri-1≠r0， ni-1≠n0，k=0，1，…，i-1。通過閉環可得到一個重要的定理。

定理1［4］：矩陣 H 對應的Tanner圖的girth至少為2(i+1)充要條件是

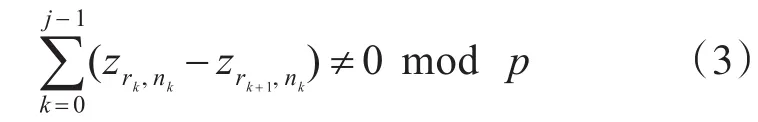
其中，2≤j≤i，0≤rk，rk+1≤m-1，0≤nk≤n-1，且r0=rr，rk≠rk+1，nk≠nk+1。 可 見 ，要 使 得girth≥2(i+1)，必須消除Tanner圖中環長小于或等于2i的環。對于陣列碼來說，由于存在r0，r1，n0，n1，r0≠r1，n0≠n1，則 (ar0-ar1)(n0-n1)≠0 ，進而得，根據定理1可知陣列碼的girth至少為6。

考慮校驗矩陣girth為8和10的兩種情況，列重分別選取3和4。對于等差陣列碼，由式（3）可化為

為了得到大girth，要盡量消除短環或減少短環的數量。首先對等差陣列碼進行分析，考慮girth為8的情況，由于陣列碼不存在4環的情況，只需從去除6環開始考慮。首先確定6環存在的條件。如果行重 r=3 ，陣列行序號 r0，r1，r2∈{0，1，2} ，由于r0，r1，r2，n0，n1，n2互不相等，存在6環的陣列列選擇必定位于不同陣列列的序號上。不失一般性，取r0=0，r1=1，r2=2，由定理1可得如表1所示第一行存在6環的約束方程，只要在校驗矩陣H選取的序列中，避免存在滿足約束方程的序列即可消除相應的環長。

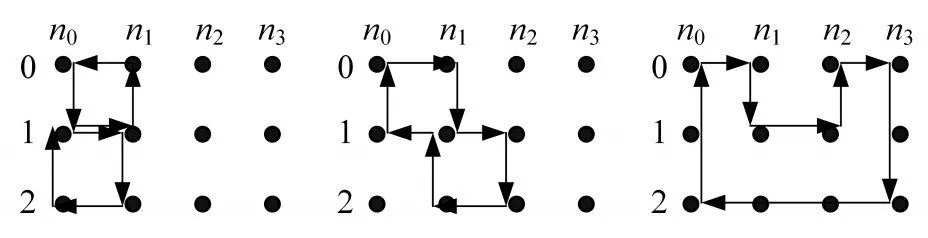
圖1 存在8環的示例

對于表1中約束方程的計算，以存在8環，行重為 3 的 情 況 為 例 ，由 于 r0，r1，r2，r3∈{0，1，2} ，n0≠n1，n1≠n2，n2≠n3，n3≠n0，n0，n1，n2，n3是兩兩不相同的，因而矩陣中存在的環路需分3種情況：列號取值范圍分別為2列、3列和4列。對應的示例圖如圖1所示。

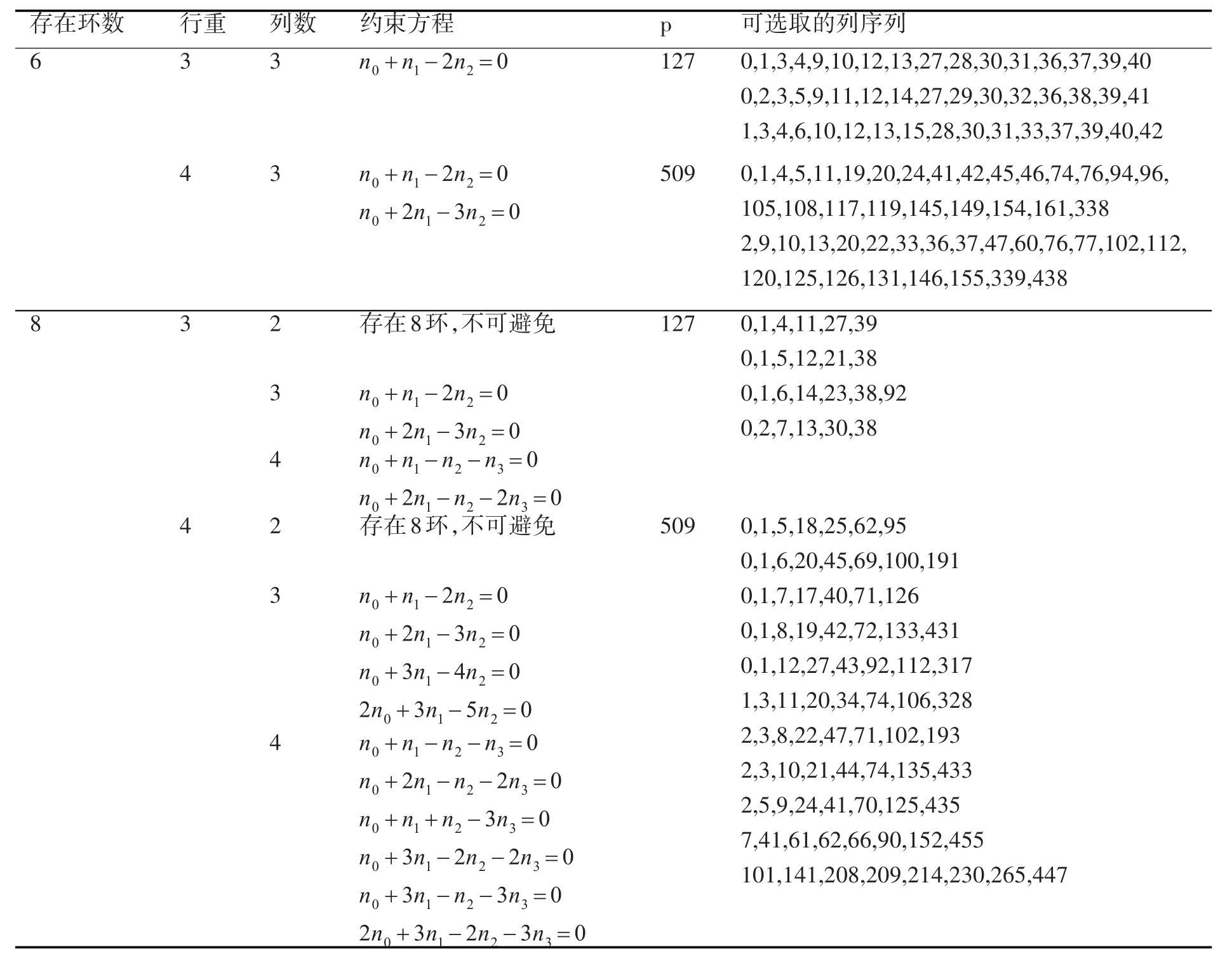
表1 6環和8環存在的約束方程和避免6環和8環的列序列

對于2列的情況，假設n0=n2，n1=n3，存在8環的約束方程為

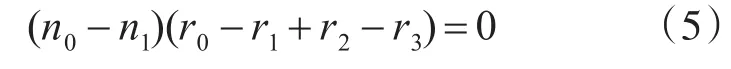
由于n0≠n1，滿足約束方程的充要條件是r0-r1+r2-r3=0。當 r0=0，r1=1，r2=2，r3=1時，其充要條件r0-r1+r2-r3=0總是會滿足的。在2列的情況下，這種8環是無法避免的。

對于3列的情況，可假設n0=n2或n1=n3，不失一般性，這里僅考慮n0=n2。存在8環的約束方程為

n0(r0-r1+r2-r3)-n1(r1-r2)+n3(r3-r0)=0（6）

由于陣列行序號 r0，r1，r2，r3∈{0，1，2}，表2給出了3列情況下存在8環不重復的約束方程。

表2 列數為3存在8環的約束方程

對于4列的情況，存在8環的約束方程為n0(r0-r1)+n1(r1-r2)+n2(r2-r3)+n3(r3-r0)=0（7）

由于陣列行序號 r0，r1，r2，r3∈{0，1，2}，表3給出了4列情況下存在8環不重復的約束方程。

表3 列數為4存在8環的約束方程

對于其他情況，分析方法與存在8環，行重為3的情況是類似的。具體的環約束方程和避免相應環的部分可選取序列如表1所示。

從上述分析可知，等差陣列碼的girth不會大于8，在兩個陣列列中，當r0=0，r1=1，r2=2，r3=1時，8環是不可避免的。而采用非等差數列碼可以在兩個不同的陣列列中避免這種8環的存在。

對于非等差數列碼，式（3）變為

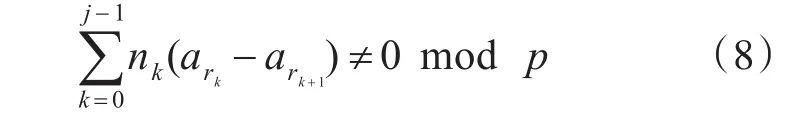
如同等差數列碼的分析，對于2列的情況，假設n0=n2，n1=n3，存在8環的約束方程為

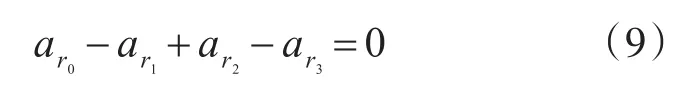
由于 ar0，ar1，ar2，ar3的集合域不在等差數列范圍內選取，因而會帶來一些優勢和問題：選擇的范圍擴大，環約束的方程相應增多，搜索序列的復雜度會相應增加；可得到girth為10或12這樣更大girth的碼字。其分析與大girth等差陣列碼中尋求陣列序列方式相同，如表4所示給出了列重為3、陣列行序號 ar0，ar1，ar2，ar3∈{0，1，3}、環長為 6和 8的約束方程以及避免相應環的列序列。

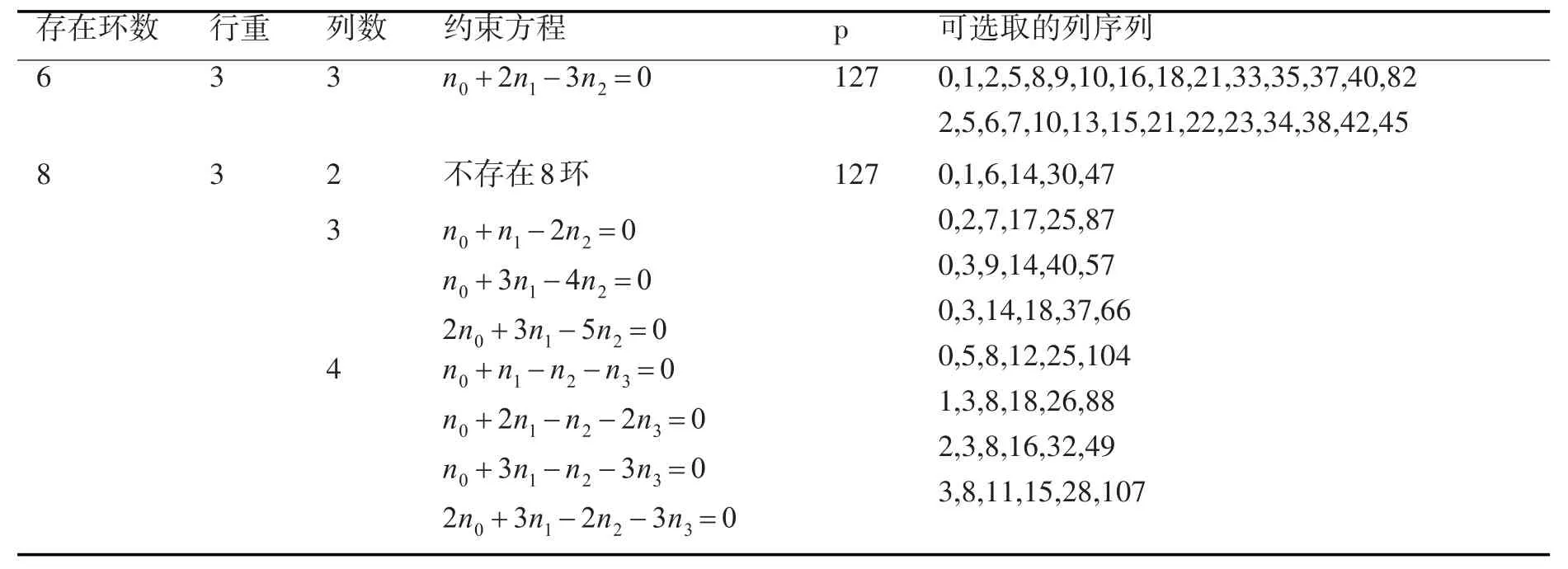
表4 非等差數列碼6環和8環存在的約束方程和避免6環和8環的列序列

2.2 大girth多進制陣列碼

根據上節約束關系選出的指數矩陣E(W)，可以保證多進制奇偶校驗矩陣H的girth都為8和10，分別避免了環長6和8。也可產生出更大girth的校驗矩陣，只是選取列序列受控的約束方程會更多，搜索的難度增大。無限增大girth最終對性能的提高也不會太大，并且陣列碼無法避免長度為12的環［11］。

對于多進制陣列LDPC碼校驗矩陣的構造將從指數矩陣E(W)出發進行擴展，且循環陣中不存在零陣。廣義多進制擴展方法基于兩個不同域：GF(p)和GF(2l)。多進制LDPC碼校驗矩陣非零值的位置由GF(p)域決定，非零值的數值由GF(2l)域決定。這兩個域的具體關系如下：(2l-1)·(rt-1)＜p＜(2l-1)·rt，其中，l∈Z，rt=

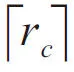
為GF(2

l

)域中所有非零元素重復的周期數，不足一個周期的，記為一個周期，并計入r

t

中，r

c

是重復周期的帶分數表示，整數部分表示的是重復的整數周期數，分數中分母表示一個周期的長度，分子表示不足一個周期的剩余長度。l與 p值的具體關系由下式表示：

其中，

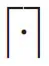
表示向上取整。

廣義二維擴展包括水平擴展和垂直擴展。首先給出水平擴展的方式，即為提出的廣義多進制位置向量。令 β是GF(2l)域的本原元。將基于GF(p)和GF(2l)域的廣義多進制位置向量定義為z(I)=(z0，z1，…，zp-1)，其中 zi=βimod(2l-1)，i∈I ，其它所有分量為0。集合I是廣義多進制位置向量中非零值所在的位置序號，多進制位置向量的重量等于集合I的勢Card(I)。定義向量的數值取值范圍是GF(2l)域中的2l-1個非零元素。當 z(I)是GF(2l)域上重量為1的 p重向量時，構造出校驗矩陣的子陣列為廣義循環置換矩陣，此時矩陣的非零位置數由指數矩陣決定；當z(I)是GF(2l)域上重量不為1的 p重向量時，構造出校驗矩陣的子陣列為廣義循環矩陣，此時非零位置數將由一個集合來決定。接著給出垂直擴展方式。令I是任一由GF(p)域中的元素組成的集合，廣義多進制位置向量z(I+1)定義為位置向量z(I)向右循環移一位，移位后第1列至第 pm-1列的元素乘以β分別得到第2列至第 p列元素，而第 p列元素則乘以βrt(2l-1)-(p-1)后得到第1列元素。根據廣義多進制位置向量的擴展規則，多進制位置向量z(I+γ)定義為集合I中元素依次加γ∈GF(p)后擴展得到的廣義多進制位置向量，在GF(2l)域上可形成以I，I+1，…，I+p-1的廣義位置向量為行的多進制p×p大小的循環矩陣PI。

二維 p重擴展可由上述垂直擴展和水平擴展兩部分組成，對于任一集合 I，dispv(I)=[I，I+1，…，I+p-1]T為該集合的垂直擴展，而disph(I)=z(I)為該集合的水平擴展，其中無論集合I中元素取GF(p)域內何值，循環矩陣PI都不會為全零矩陣。集合I與循環置換矩陣PI是一一對應的關系：

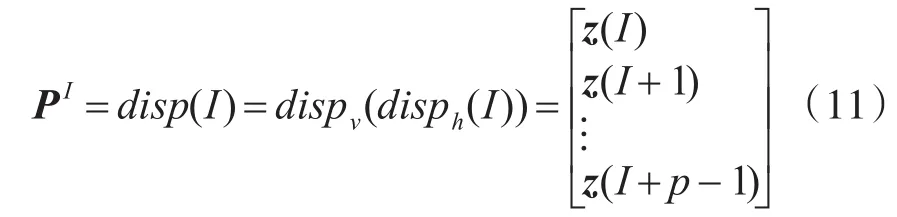
通過式（11）可從指數矩陣（對應于廣義循環置換矩陣）或相應集合（對應于廣義循環矩陣）構造出具有廣義循環特性的多進制校驗矩陣H。由于多進制校驗矩陣非零值位置和數值的選取分別建立在GF(p)和GF(2l)兩個不同的域上，構造出的二維 p重矩陣PI非零元素的分布具有兩種情形：1）當rt=1時，在GF(2l)域上只具有部分域元素循環（rc＜1）或循環（rc=1）的特性；2）當 rt≥2時，所有GF(2l)域非零元素個數一般在矩陣中分布不均，但是當2l-1=rcp時，非零元素分布將是均勻的。為了便于表示，PI簡化記為 Hi，j，由擴展的性質知Hi，j是廣義循環矩陣，因此其可分解為一個非奇異的對角矩陣Y和一個循環矩陣之積。將 Hi，j表示為兩個 p×p矩陣Y和的 乘 積 ，即，其中是一個 GF(2l)域上不具有乘 β性質的移位循環矩陣，如果單獨來看，它是一個二進制矩陣，非零元素取值選自GF(q)域中的某個非零值，Y是一個以部分周期循環元素β0，β，…，β2l-2，β0，β，… 為主對角線，其余為 0 的p×p大小的方陣，記為Y=diag(β0，β，…)。設 c為碼字向量，則，可知，與是等價的。所以說，矩陣和的零空間給出的碼字是一樣的。因此，通過可以找到具有系統或部分系統形式的生成矩陣，以實現有效的線性復雜度編碼［10］。可以說通過廣義位置向量擴展生成的多進制LDPC碼充分考慮了編碼和譯碼的實現復雜度，在編碼上，由于校驗矩陣是廣義QC形式的矩陣，繼承了QC矩陣的特性，可采用QCLDPC碼的有效編碼方法；在譯碼上，通過廣義二維擴展，數值域建立在2的冪次上，使得譯碼可以采用高性能低復雜度的軟判決譯碼算法，利于工程應用。

3 仿真結果及性能分析

本節將對構造的大girth多進制陣列LDPC碼進行仿真比較，仿真中的信號均采用BPSK調制，且在雙邊功率譜密度為N02的AWGN信道中傳輸。譯碼采用FFT-QSPA算法且最大迭代次數設置為50，仿真中的誤碼率是在檢測50幀錯誤的條件下得出的。為了便于比較，對于等差陣列碼和非等差陣列碼，取 p=127，其子陣列的大小為127×127，選擇的列重都為3，行重都為6，因此，r=3，n=6。根據碼的性質、girth和等差陣列碼的數值域選擇的不同構造出8種不同的多進制LDPC碼。在構造出的LDPC碼中，從構造性質的角度，有等差陣列碼和非等差陣列碼；從girth的角度，有girth為8和10的碼；從數值構造域的角度，有128進制、64進制和32進制LDPC碼。

仿真中等差陣列碼陣列行序號選{0，1，2}，非等差陣列碼陣列行序號選{0，1，3}。girth大小的選擇按照表1和表4中給出的序列來抽取指數矩陣中相應的列。對于數值域GF(2l)選擇如下：當l=7時，rt=1，rc=1，此時矩陣中元素分布是均勻的；當 l=6時，rt=3，；當 l=5時，rt=5，。根據三種GF(2l)域選擇構造出不同的多進制LDPC碼，但是選擇的指數矩陣都是相同的。等差數列情況，R3G8碼（3表示列重，8表示girth值）的指數矩陣為

R3G10碼的指數矩陣為

非等差數列情況，R3G8碼的指數矩陣為

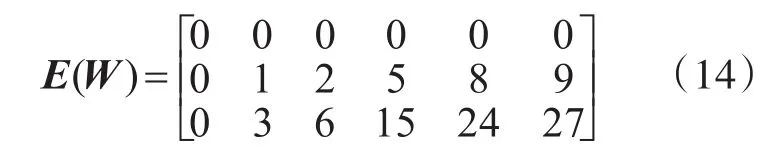
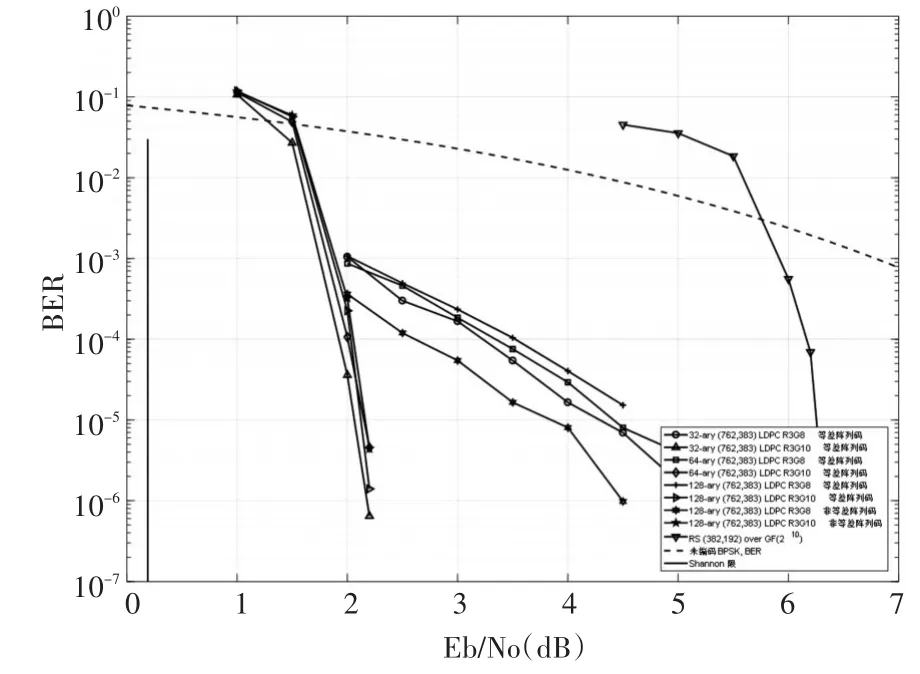
圖1 不同參數的多進制（762，383）陣列LDPC碼的誤碼性能比較

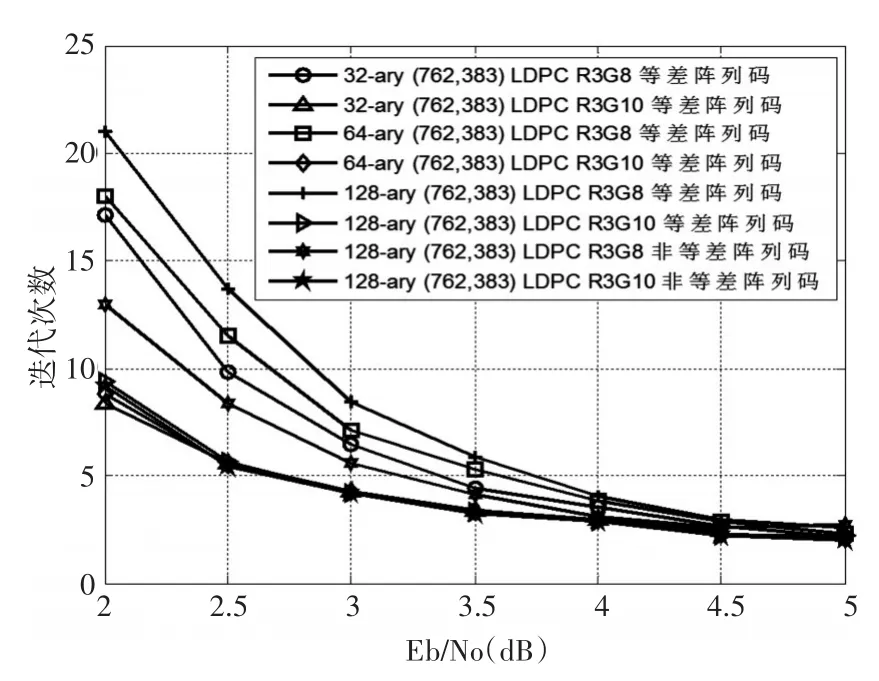
圖2 不同參數的多進制（762，383）陣列LDPC碼的迭代性能比較

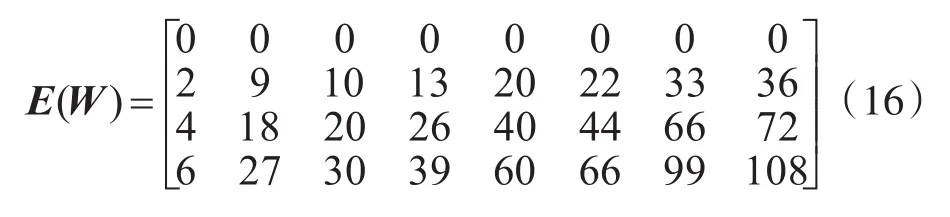
R3G10碼的指數矩陣為

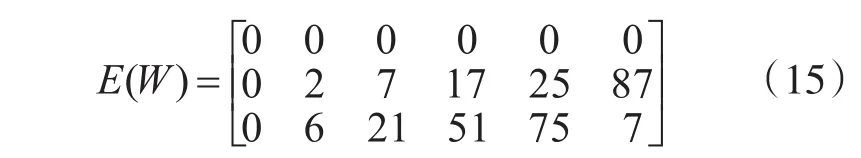
8種多進制（762，383）陣列LDPC碼的誤碼性能和迭代性能分別如圖1和圖2所示。其中等差陣列R3G10碼是存在8環的，但是通過列陣列的選取還是可以消除大部分存在的8環。為了便于比較，圖1也給出了RS碼BM算法的誤碼性能，在誤比特率（BitErrorRate，BER）為 10-5處，32進制（762，383）R3G8LDPC 碼相對于 GF(210)域（382，192）RS碼來說，取得了大約4.24dB的編碼增益。從圖1和圖2還可以得出：1）非等差陣列碼在girth為8時取得的性能優于等差陣列碼，但是girth為10時，其優勢就不太明顯了；2）盡管有的碼只是部分消除了8環，但是girth為10的碼比girth為8的碼取得了更大的編碼增益；3）等差陣列碼中，隨著進制數的減少，其性能越好，收斂越快，但是之間的差距并不大。進制數的減少同時也能降低譯碼的復雜度。對于結論3）這種現象Mackay也曾指出［1，12］：隨著域階數的增加，其誤碼性能并不總是單調提升，這一現象的產生與校驗矩陣的構造密切相關。

下面考慮列重為4的大girth多進制LDPC碼的性能。參數選取如下：p=509，l=6，這樣構造出的廣義多進制準循環校驗矩陣位置和數值的選擇分別基于GF(509)和GF(64)域，列重為4，行重為8，子陣列的大小為 509×509，rt=9，。

R4G8碼的指數矩陣為

R4G10碼的指數矩陣為

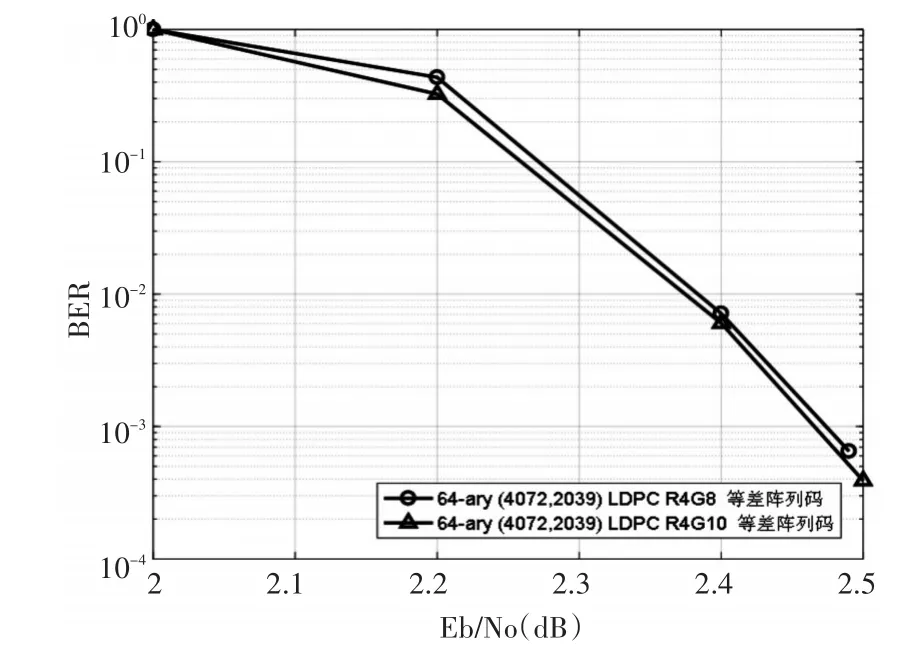
圖3 64-ary（4072，2039）陣列LDPC碼的誤碼性能曲線

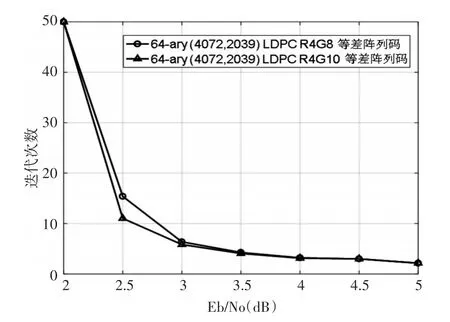
圖4 64-ary（4072，2039）陣列LDPC碼的迭代性能曲線

由上述兩個指數矩陣構造的校驗矩陣大小都為2036×4072矩陣的秩同為2033，其零空間給出了碼率為0.5007的64-ary（4072，2039）陣列LDPC碼，其誤碼性能和迭代性能分別如圖3和圖4所示。從仿真結果來看，girth為10的碼取得性能略優于girth為8的碼。

4 結語

大girth及其分布是保證碼字性能的一個重要因素之一。為了構造大girth多進制LDPC碼，從指數矩陣出發，選出避開短環的陣列列，并將廣義二維擴展方法應用于指數矩陣，構造出不存在短環的校驗矩陣。仿真結果表明，基于廣義二維擴展方法的多進制大girth陣列LDPC碼能取得良好的性能，利于有效的編譯碼，可減少存儲空間。構造出的校驗矩陣在一定程度上增大girth能明顯提高碼字的性能，保證信息的可靠傳輸，滿足無線通信的高頻帶利用率。