渡槽排架結構環境激勵模態試驗

顧培英，劉冬梅，鄧 昌，湯 雷

(1.南京水利科學研究院材料結構研究所，江蘇 南京 210029； 2.水利部水科學與水工程重點實驗室，江蘇 南京 210029；3.南京科技職業學院建筑與藝術設計學院，江蘇 南京 210048)

國內外對混凝土壩與橋梁工程安全評價、混凝土結構老化病害評估與損傷診斷已開展大量研究，筆者對大體積混凝土結構整體安全性進行了初步探討[1-5]，但國內外對渡槽結構安全評價的研究較少。筆者提出了基于振動診斷技術的大跨度高架渡槽結構安全評價技術，已對渡槽結構典型破壞特征有了較為全面的了解[6]，根據模態頻率、振型、阻尼模態參數分析結果[7]，評價結構安全狀況。模態試驗分析是獲得模態參數的主要手段，模態參數識別方法有頻域法和時域法，其中時域法應用較廣泛。

模態試驗按輸入輸出方式可分為單輸入單輸出(single input single output, SISO)、單輸入多輸出(single input multiple output, SIMO)、多輸入單輸出(multiple input single output, MISO)和多輸入多輸出(multiple input multiple output, MIMO)。從某種意義上講模態試驗方法可劃分為SIMO、MIMO兩大類[7]。

實際大型結構往往在風力、水流、交通等自然力或工作狀態下能激勵出識別模態參數的振動響應，無需且往往現場也無法施加人工激勵。本文從未考慮渡槽槽身的排架入手，通過單向SIMO法、雙向MIMO法環境激勵模態試驗，提出排架類結構環境激勵模態試驗建議方法。

1 增強頻域分解法

頻域分解(frequency domain decomposition，FDD)法是根據結構在環境激勵下的振動響應，得到反映真實動力特性的模態參數[8]，該方法由峰值拾取法發展而來[9]。FDD 方法最早由 Brincker 等在復模態指示函數的基礎上提出，在滿足白噪聲激勵假設和小阻尼假設時，能夠識別模態頻率和模態振型[8]。Brincker等隨后提出了增強頻域分解法(enhance frequency domain decomposition，EFDD)，將經奇異值分解后的單自由度功率譜進行傅里葉逆變換，得到對應的自相關函數，從而通過對數衰減法獲得模態頻率和阻尼比[9]。

設x(t)是未知不能測量的激勵，第k個離散時間點測量的響應數據為y(k)，對欠阻尼的情況，有

Gyy(jω)=H*(jω)Gxx(jω)HT(jω)

(1)

式中:Gxx(jω)、Gyy(jω)分別為輸入、輸出功率譜密度函數矩陣；H(jω)為頻響函數矩陣；ω為頻率；上標*表示復共軛，下同。

輸入與輸出功率譜密度函數矩陣均為共軛對稱矩陣。當所關心頻段內假設輸入為一白噪聲，具有平直譜，則Gxx(jω)為一實常數對角矩陣，用符號D表示該對角矩陣。交通和風引起的地脈動等寬帶隨機激勵，或自然界的脈沖激勵，均可認為具有平直譜[10]。

H(jω)也可用留數表示：

(2)

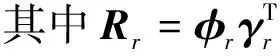
式中：Rr為第r階模態留數矩陣；φr、γr分別為第r階模態振型和模態參與向量；λr為第r階極點；n為模態階數。

將式(2)代入式(1)，響應譜矩陣變換為

(3)

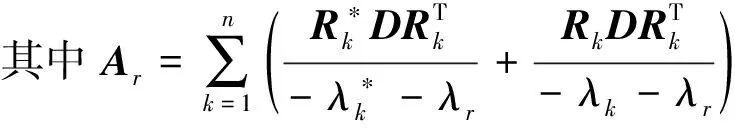
式中：Ar為相關的留數項；上標H表示共軛轉置，下同。

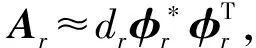
(4)

式中：Ψ為特征矢量矩陣;diag(·)表示對角矩陣。

Gyy(jω)為共軛對稱矩陣，對其進行奇異值分解，有

(5)

式中：U為奇異值向量組成的酉矩陣；V為奇異值構成的實數對角矩陣。

奇異值向量與模態振型相對應，而奇異值則等于2dr除以頻率點到極點距離的實部。最大奇異值所在位置即為該階模態頻率。

頻域分解法核心是對響應功率譜進行奇異值分解，將功率譜分解為對應多階模態的單自由度系統功率譜。該方法識別精度較高，抗干擾能力較強。但3個假設必須同時滿足：①激勵為白噪聲；②結構阻尼為小阻尼；③當有密集模態時，模態必須正交。

2 試驗方案

將渡槽排架柱與橫梁統稱為渡槽排架結構，根據新疆某渡槽，主要構件按1∶15幾何比尺制作2榀小型渡槽排架鋼筋砂漿結構[7]，記為1號排架、2號排架。

環境激勵模態試驗裝置一般包括傳感及信號放大設備、信號采集設備、信號分析系統。選用CA-YD-107加速度傳感器、INV-8 多功能抗混濾波放大器、INV306U-6260智能信號采集處理分析儀、DASP智能數據采集和信號分析系統。共布置37個測點，其中測點1為參考點，分多組測試，部分試驗照片及測點位置編號如圖1所示。對于本小型排架結構，由于模態頻率較高，室內試驗環境安靜，仍需借助錘擊模擬環境激勵，盡量避開模態節點，在測點6附近激勵，但不需測試激勵信號。

圖1 部分試驗照片及測點位置編號

3 模態試驗結果及分析

3.1 縱向模態識別結果及分析

3.1.11號排架

1號排架環境激勵下縱向模態響應功率譜奇異值曲線如圖2所示，盡量在峰值處收取模態主峰，收取了11階模態。

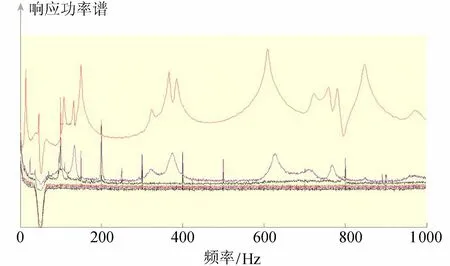
圖2 1號排架環境激勵下縱向模態響應功率譜奇異值曲線

1號排架環境激勵下縱向模態振型相關MAC矩陣校驗如圖3所示。采用MAC矩陣非對角線元素平均值、最大值作為評價指標，二者數值越小越好。孫正華等[11-12]提出，工程上一般當MAC矩陣非對角線元素小于0.25時，可近似認為兩個模態正交，因此0.25可作為閾值普遍應用于傳感器優化布置研究中。本文將0.25作為兩模態識別效果好壞的閾值。

根據圖3，大多數非對角線元素很小，接近于0，90.9%的非對角線元素小于0.25，平均0.115 5，說明大多數模態振型具有較好的正交性，識別精度較高。MAC0607、MAC0809(式中下標06、07分別代表第6階、第7階模態，其余類推)分別為0.263 5、0.310 4，略大于0.25，識別效果尚可；MAC1011最大，為0.732 5；MAC0810、MAC0910次之，分別為0.430 2、0.440 7。這說明第10階與第11階模態正交性較差，第8階與第10階、第9階與第10階次之。

圖3 1號排架環境激勵下縱向模態振型相關MAC矩陣校驗

前11階模態振型如圖4所示。根據圖2、圖4，1號排架縱向模態除第5階譜峰較小，第5階、第10階、第11階模態振型較差外，其他模態識別效果較好。

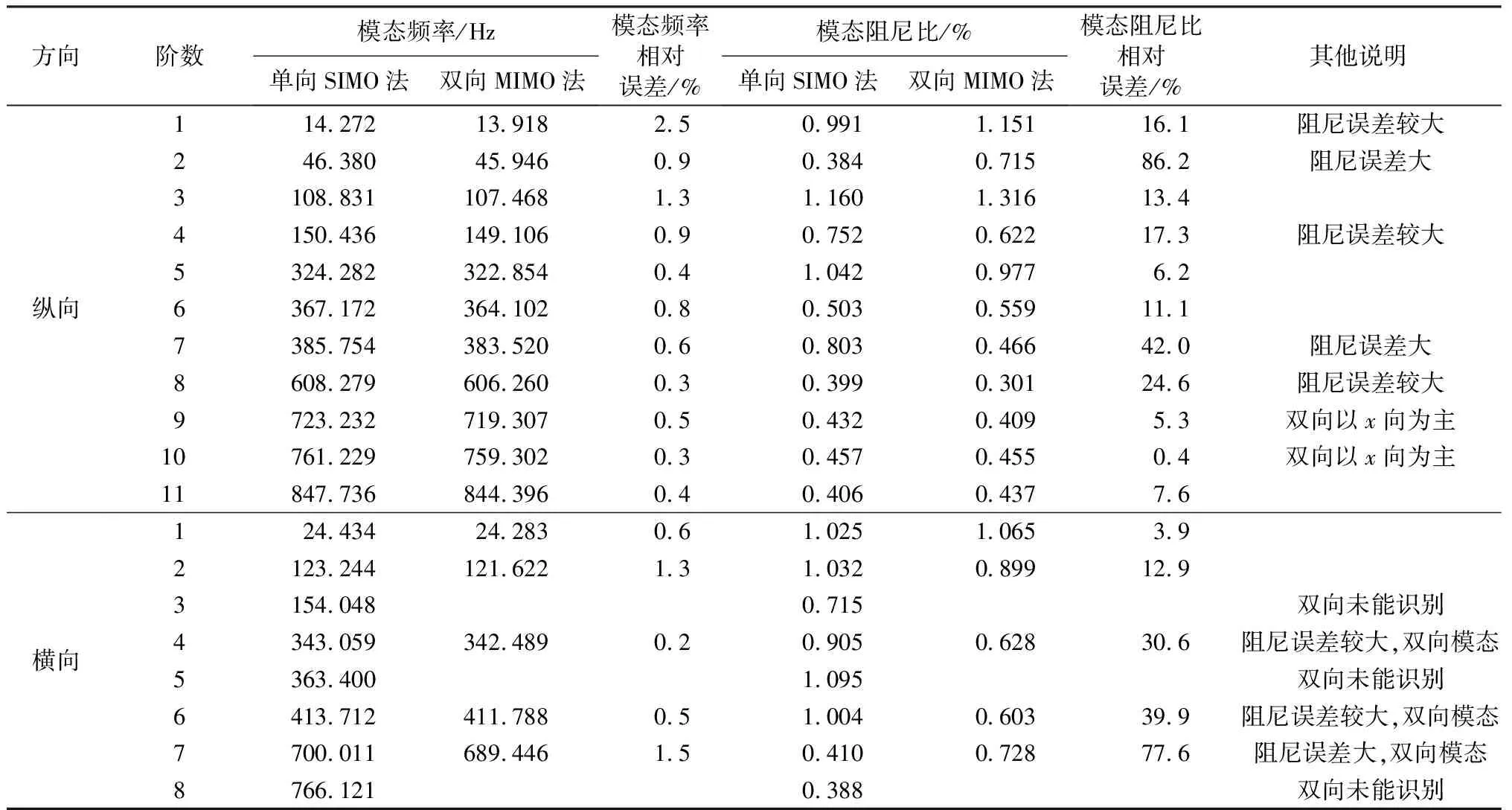
1號排架環境激勵下縱向模態參數識別結果見表1。由表1可知，1號排架縱向模態阻尼比為0.384%～1.160%，平均0.666%，阻尼偏小，但仍在正常范圍內[7]。柯國軍等[13]試驗得到普通混凝土阻尼比在0.9%～2.0%之間，輕骨料混凝土阻尼比小于普通混凝土，一般小于1.0%。同一材料，不同結構形式、不同模態振型、不同截面形式，阻尼比可能相差很大。本模型為砂漿結構，阻尼偏小。一般情況下阻尼識別精度較低、離散性大，本文對模態阻尼不作重點分析。

3.1.22號排架

2號排架縱向模態試驗分析結果與1號排架相似，也識別出前11階模態(圖略)。

同樣，根據模態振型相關MAC矩陣校驗圖(圖略)，大多數非對角線元素很小，接近0，89.1%非對角線元素小于0.25，平均0.120 6，大多數模態振型具有較好的正交性，識別精度較高。MAC0607、MAC0507分別為0.288 7、0.304 8，略大于0.25，識別效果尚可；MAC1011最大，為0.801 8；MAC0810、MAC0809、MAC0910次之，分別為0.365 0、0.392 0、0.455 9，表明第10階與第11階模態正交性較差，第8階與第10階、第8階與第9階、第9階與第10階次之。

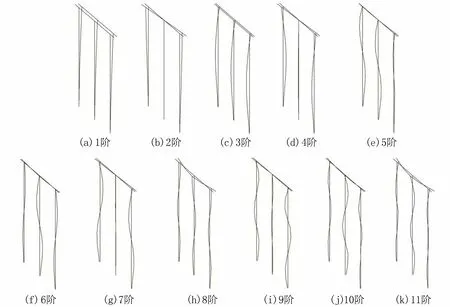
圖4 1號排架環境激勵下縱向前11階模態振型

方向階數模態頻率/Hz單向SIMO法雙向MIMO法模態頻率相對誤差/%模態阻尼比/%單向SIMO法雙向MIMO法模態阻尼比相對誤差/%其他說明縱向橫向114.27213.9182.50.9911.15116.1阻尼誤差較大246.38045.9460.90.3840.71586.2阻尼誤差大3108.831107.4681.31.1601.31613.44150.436149.1060.90.7520.62217.3阻尼誤差較大5324.282322.8540.41.0420.9776.26367.172364.1020.80.5030.55911.17385.754383.5200.60.8030.46642.0阻尼誤差大8608.279606.2600.30.3990.30124.6阻尼誤差較大9723.232719.3070.50.4320.4095.3雙向以x向為主10761.229759.3020.30.4570.4550.4雙向以x向為主11847.736844.3960.40.4060.4377.6124.43424.2830.61.0251.0653.92123.244121.6221.31.0320.89912.93154.0480.715雙向未能識別4343.059342.4890.20.9050.62830.6阻尼誤差較大,雙向模態5363.4001.095雙向未能識別6413.712411.7880.51.0040.60339.9阻尼誤差較大,雙向模態7700.011689.4461.50.4100.72877.6阻尼誤差大,雙向模態8766.1210.388雙向未能識別

注：表中x向代表渡槽縱向。

2號排架環境激勵下縱向模態參數識別結果見表2。由表2可知，模態阻尼比為0.381%～1.554%，平均0.796%，阻尼總體略大于1號排架，仍偏小，但仍在正常范圍內。此外，2號排架縱向各階模態頻率略低于1號排架，除1階相差較大(約13.3%)外，其余較小，在2.5%～6.0%之間，平均4.0%。

3.1.3排架縱向模態規律

綜合分析得出排架縱向模態有以下規律：

a. 識別出11階縱向模態，響應功率譜奇異值曲線絕大多數譜峰明顯，大多數模態識別效果較好，尤其是低階模態。

b. 排架結構以排架柱彎曲振動為主，低階模態橫梁以平動或轉動剛體振動為主，高階模態橫梁以彎曲振動為主。

c. 除第10階與第11階模態正交性較差，第8階與第10階、第9階與第10階次之，2號排架第8階與第9階模態正交性也稍差外，大多數模態振型具有較好的正交性。

3.2 橫向模態識別結果及分析

3.2.11號排架

1號排架環境激勵下橫向模態響應功率譜奇異值曲線如圖5所示，收取了8階模態。

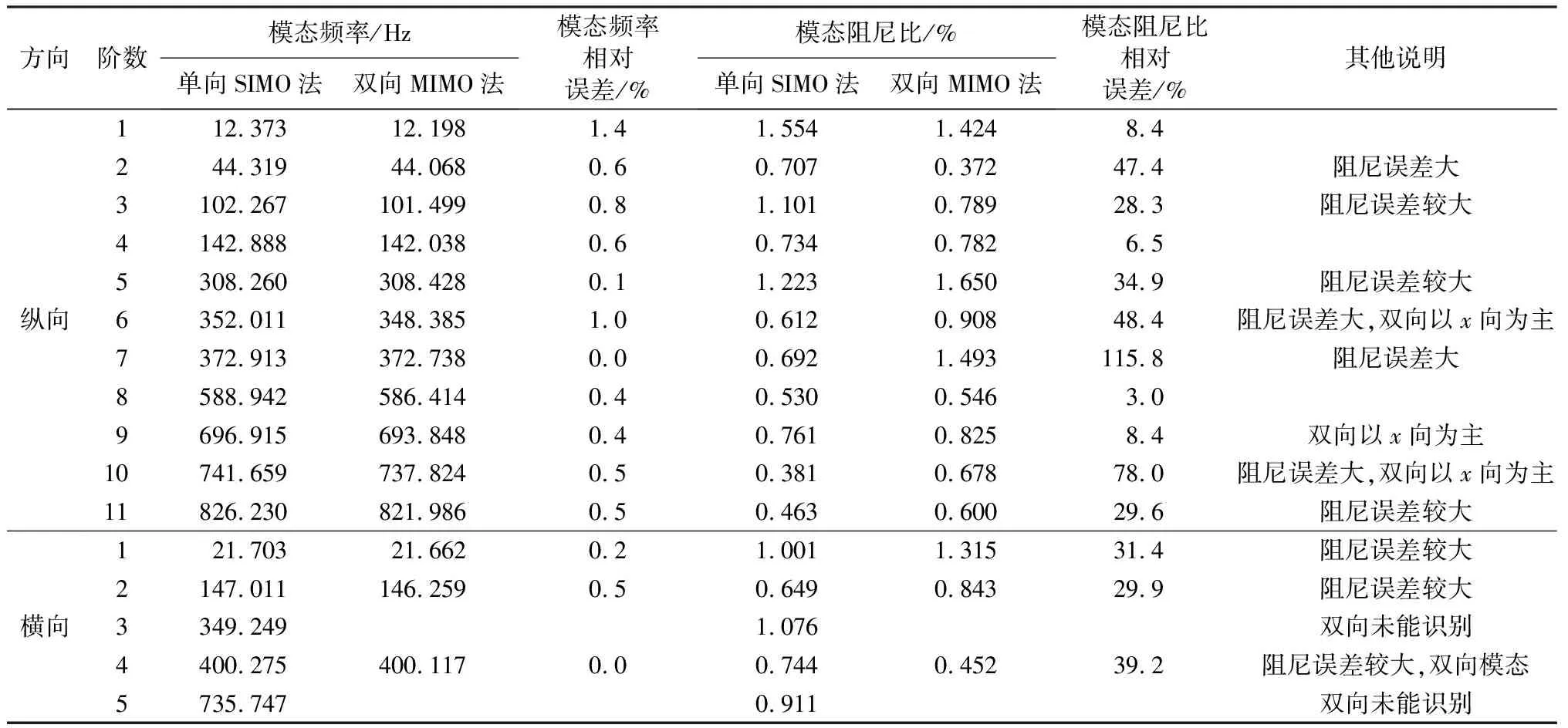
表2 2號排架環境激勵下模態參數識別結果

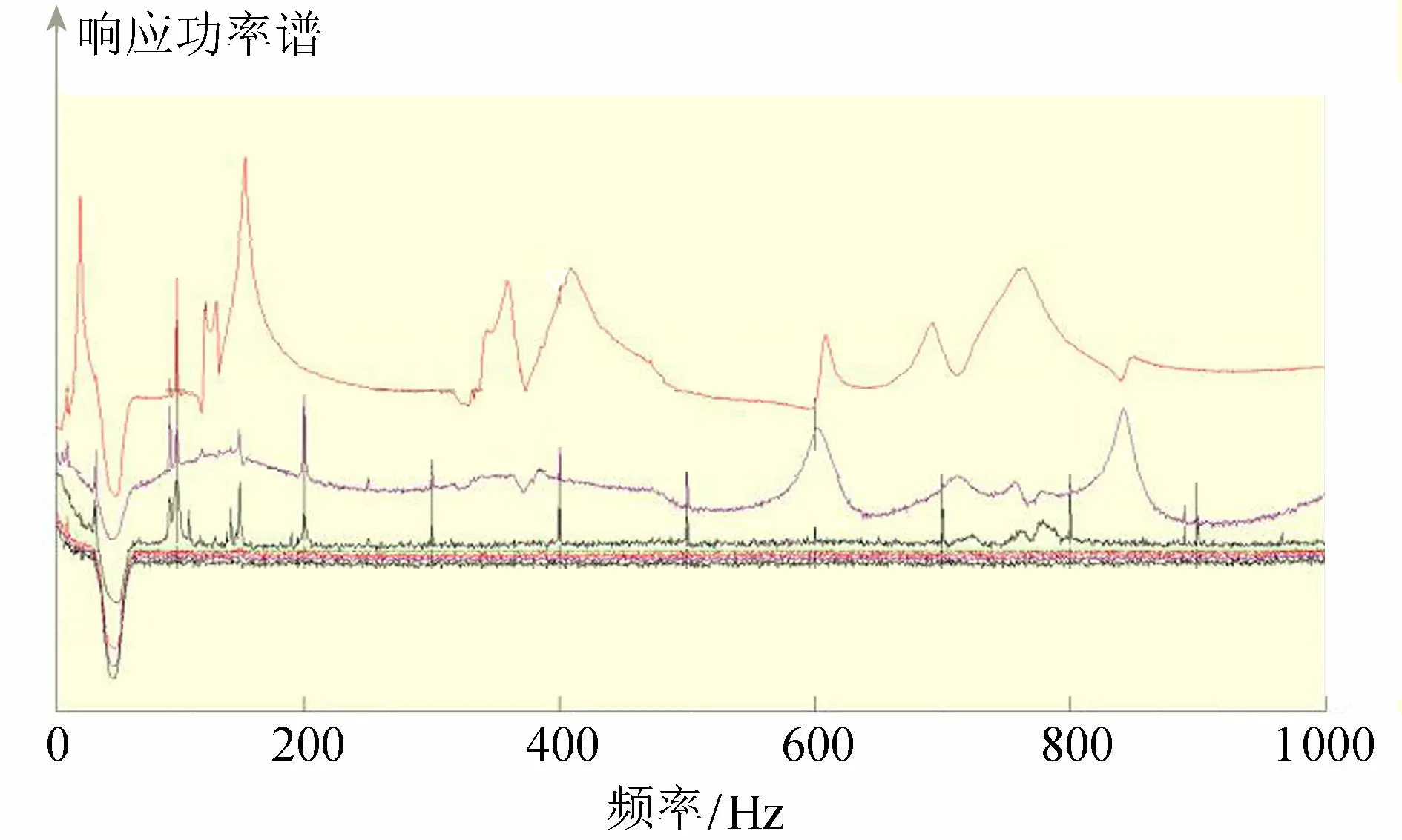
圖5 1號排架環境激勵下橫向模態響應功率譜奇異值曲線

模態振型相關MAC矩陣(圖略)大多數非對角線元素較小，平均0.184 6，最大值MAC0708為0.551 8，有32.1%的非對角線元素大于0.25，67.9%的模態振型具有較好的正交性。總的來說，環境激勵下橫向模態沒有縱向正交性好，識別精度也沒有縱向高。

1號排架環境激勵下橫向模態參數識別結果見表1，前8階模態振型如圖6所示。由表1可知，模態阻尼比為0.388%～1.095%，平均0.822%，阻尼偏小，但仍可認為該阻尼在正常范圍內。

根據功率譜奇異值曲線、模態振型圖，相對而言，1號排架環境激勵下橫向模態譜峰沒縱向明顯及豐富，第2階、第5階、第7階譜峰較小，第4階幾乎無譜峰，第4階、第5階、第7階、第8階模態振型較差或略差，其他4階即50.0%的模態識別效果較好。總之，橫向模態沒縱向豐富，識別效果也沒縱向好。

圖6 1號排架環境激勵下橫向前8階模態振型

3.2.22號排架

2號排架橫向收取了5階模態(圖略)，模態振型相關MAC矩陣(圖略)大多數非對角線元素較小，平均0.197 9，最大值MAC0304為0.459 2，有30.0%的非對角線元素大于0.25，70.0%的模態振型具有較好的正交性。

根據功率譜奇異值曲線、模態振型圖，2號排架環境激勵下橫向模態譜峰沒有縱向明顯及豐富，也無1號排架橫向模態豐富，第3階無譜峰，第3階、第5階模態振型較差或略差，其他3階即60.0%的模態識別效果較好。

2號排架環境激勵下橫向模態參數識別結果見表2，根據表2，模態阻尼比在0.649%～1.076%之間，平均0.876%，阻尼偏小，但仍在正常范圍內。另外，2號排架橫向對應模態頻率略低于1號排架，除1階相差較大，約11.2%外，其余較小，在3.2%～4.6%之間，平均3.9%。

3.2.3排架橫向模態規律

a. 識別出5～8階橫向模態，功率譜奇異值曲線譜峰沒有縱向明顯及豐富，只有50.0%～60.0%的模態譜峰明顯、識別效果較好。

b. 排架結構以排架柱彎曲振動為主，橫梁為平動或不動的剛體振動。

c. 67.9%～70.0%的模態振型具有較好的正交性。

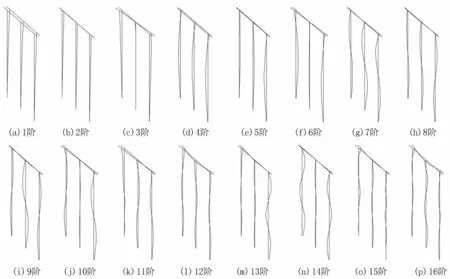
圖8 1號排架環境激勵下雙向前16階模態振型

3.3 雙向模態識別結果及分析

3.3.11號排架

1號排架環境激勵下雙向模態響應功率譜奇異值曲線如圖7所示，收取了16階模態。

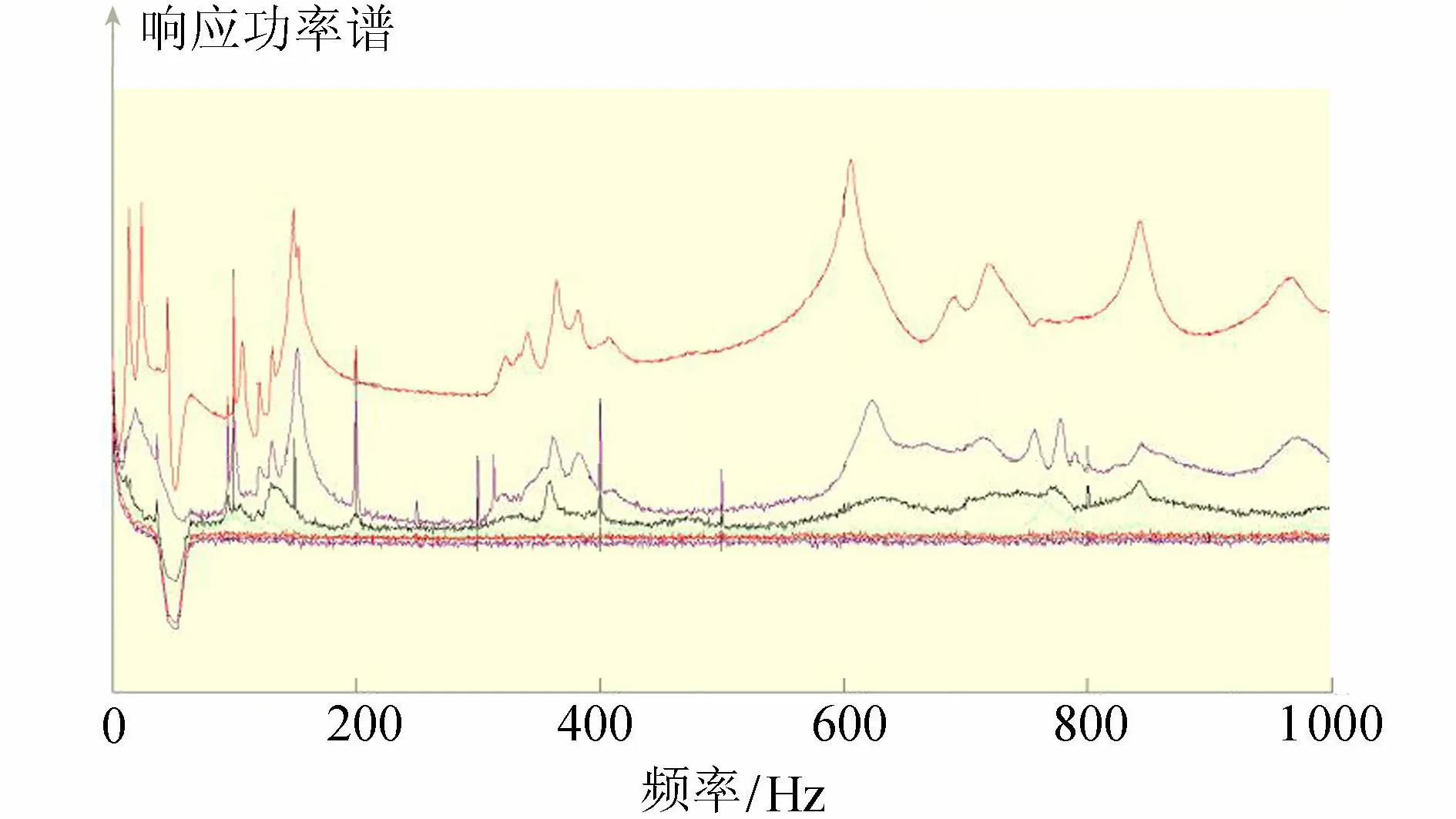
圖7 1號排架環境激勵下雙向模態響應功率譜奇異值曲線

模態振型相關MAC矩陣(圖略)大多數非對角線元素很小，接近0，平均0.114 2，大多數模態振型正交性較好，模態識別精度較高。MAC0809、MAC0911、MAC1213、MAC1215、MAC1216略大于0.25，識別效果尚可；MAC1415最大，為0.693 8；MAC0708、MAC0910、MAC1011、MAC1314、MAC1315次之，為0.381 2～0.534 6，表明第14階與第15階模態正交性較差，第7階與第8階、第9階與第10階、第10階與第11階、第13階與第14階、第13階與第15階次之。對應單向SIMO法環境激勵，相當于縱向第9階與第10階正交性較差，縱向第5階與橫向第4階、縱向第6階與7階、縱向第7階與橫向第6階、橫向第7階與縱向第9階、橫向第7階與縱向第10階次之。由此可知，雙向MIMO法環境激勵識別出的模態，低階模態識別精度較理想，高價模態較差。

1號排架環境激勵下雙向模態參數識別結果見表1，前16階模態振型如圖8所示。由表1可知，模態阻尼比為0.301%～1.316%，平均0.708%，阻尼偏小，但仍在正常范圍內。

根據圖7、圖8，1號排架環境激勵下雙向模態試驗共識別出11階縱向或以縱向為主的模態，其中有8階譜峰明顯或較明顯，有3階譜峰較小，可見縱向或以縱向為主的模態譜峰大多數明顯；識別出2階橫向或以橫向為主的模態，其中第2階(即橫向第1階)譜峰明顯，第5階(即橫向第2階)較小，另外3階單向模態試驗識別出的橫向模態在雙向模態試驗中呈雙向模態，即第8階、第11階、第13階，譜峰較小或幾乎無譜峰，還有3階橫向模態未能識別。第8階與單向SIMO法模態振型不同，為雙向模態；第10階、第16階模態略差；第11階、第13階、第15階模態較差；其他10階模態識別效果較好。總之，識別出的橫向模態沒有縱向模態豐富，識別效果也沒縱向好。

3.3.22號排架

2號排架雙向收取了14階模態(圖略)。模態振型相關MAC矩陣(圖略)大多數非對角線元素很小，接近0，平均0.115 5，大多數模態振型正交性較好，模態識別精度較高。MAC1114略大于0.25，識別效果尚可；MAC1213最大，為0.632 7；MAC0506、MAC0809、MAC0910、MAC1314次之，為0.431 4～0.558 4，表明第12階與第13階模態正交性較差，第5階與第6階、第8階與第9階、第9階與第10階、第13階與第14階次之。對應單向SIMO法，相當于縱向第9階與第10階正交性較差，縱向第4階與橫向第2階、縱向第6階與第7階、縱向第7階與橫向第4階、縱向第10階與第11階次之。

2號排架環境激勵下雙向模態參數識別結果見表2。根據表2，模態阻尼比為0.372%～1.650%，平均0.906%，阻尼偏小，但仍在正常范圍內。

根據功率譜奇異值曲線、模態振型圖，2號排架環境激勵下雙向模態試驗共識別出11階縱向或以縱向為主的模態，與1號排架類似；識別出2階橫向或以橫向為主的模態，其中第2階譜峰明顯，第6階(即橫向第2階)較小，另外1階單向模態試驗識別出的橫向模態在雙向模態試驗中呈雙向模態，即第10階，譜峰較小，還有2階橫向模態未能識別。第13階、第14階模態略差；第9階、第10階模態較差；其他10階模態識別效果較好。

3.3.3排架雙向模態規律

綜合分析得出2號排架環境激勵下雙向MIMO法環境激勵識別出的模態規律與1號排架類似，只是2號排架雙向只識別出14階(1號排架16階)，具體規律如下：

a. 環境激勵下雙向模態試驗識別出14～16階模態，其中縱向或以縱向為主的模態譜峰大多數明顯，橫向或以橫向為主、雙向模態譜峰除第2階明顯外，其他較小，有的幾乎無譜峰，有的甚至未能識別。

b. 排架結構以排架柱彎曲振動為主，低階模態下橫梁以平動或轉動的剛體振動為主，高階模態下橫梁以彎曲振動為主。

c. 大多數模態振型具有較好的正交性。

d. 雙向MIMO法環境激勵識別出的模態，低階模態識別精度較為理想，高價較差。

3.4 雙向與單向模態識別結果比較分析

綜合前面分析結果，得到以下幾點規律：

a. 單向SIMO法縱向模態功率譜奇異值曲線大多數譜峰明顯，大多數模態識別效果較好，橫向只有50.0%～60.0%的模態譜峰明顯，縱向模態比橫向模態豐富，識別效果也優于橫向模態。

b. 雙向MIMO法識別出的縱向或以縱向為主的模態譜峰絕大多數明顯，橫向或以橫向為主、雙向模態譜峰除雙向第2階明顯外，其他較小，有的幾乎無譜峰，有的甚至未能識別。

c. 排架結構以排架柱彎曲振動為主，縱向低階模態下橫梁以平動或轉動的剛體振動為主，縱向高階模態下橫梁以彎曲振動為主，橫向模態橫梁為平動或不動的剛體振動。

d. 大多數模態振型具有較好的正交性。

值得一提的是，前兩點規律說明雙向MIMO法容易漏掉排架橫向模態，從振動能量角度而言，渡槽排架模態振型所占能量以縱向為主，橫向模態能量遠低于縱向。

根據表1，1號渡槽排架環境激勵下單向SIMO法與雙向MIMO法模態頻率相差較小，平均誤差0.8%，最大2.5%。但識別出的模態阻尼比變化較大，因為阻尼比值偏小，誤差難免會偏大，50.0%的模態阻尼比誤差大于15.0%，最大誤差達86.2%，其余50.0%的模態誤差在0.4%～13.4%之間，平均7.6%。前面也已介紹，一般情況下模態阻尼比識別精度較低，離散性大，環境激勵獲得的大多數模態阻尼比在正常范圍，誤差可接受。

根據表2，2號渡槽排架環境激勵下單向SIMO法與雙向MIMO法模態頻率相差很小，平均0.5%，最大1.4%。大多數模態阻尼比誤差偏大，但阻尼比仍在正常范圍內。

綜合表1、表2，單向SIMO法與雙向MIMO法識別出的模態頻率誤差較小，模態阻尼均在正常范圍內，誤差較大，應用雙向MIMO法部分橫向模態未能準確識別。當然雙向MIMO法也識別出少部分SIMO法不能全面識別的雙向模態。對于環境激勵，若時間、經費充足，可以同時進行單向SIMO法與雙向MIMO法試驗分析，相互驗證、相互補充。

排架這種平面特性明顯的結構以單向模態為主[7]。從模態識別精度本身而言，按兩方向分別進行單向SIMO環境激勵模態試驗，大多數模態結果較為可靠，尤其是低階模態，這也能滿足實際工程需要。所以，從模態識別精度、試驗工作量，兼顧操作便捷性而言，排架結構模態試驗選擇SIMO單向環境激勵模態試驗優于雙向MIMO法。

4 結 論

a. 單向SIMO法縱向模態功率譜奇異值曲線絕大多數譜峰明顯，大多數模態識別效果較好，橫向只有50.0%～60.0%的模態譜峰明顯，縱向模態比橫向模態豐富，識別效果也優于橫向模態。

b. 雙向MIMO法識別出的縱向或以縱向為主的模態譜峰大多數明顯，橫向或以橫向為主、雙向模態譜峰除雙向第2階明顯外，其他較小，有的幾乎無譜峰，甚至未能識別。

c. 排架結構以排架柱彎曲振動為主，縱向低階模態橫梁以平動或轉動剛體振動為主，縱向高階模態橫梁以彎曲振動為主，橫向模態橫梁為平動或不動剛體振動。

d. 單向SIMO法和雙向MIMO法識別出的大多數模態振型具有較好的正交性。

e. 環境激勵下單向SIMO法與雙向MIMO法識別出的模態頻率誤差較小，模態阻尼誤差偏大，但仍在正常范圍內，盡管雙向MIMO法識別出少部分SIMO法不能全面識別的雙向模態，但部分橫向模態未能準確識別。平面特性明顯的排架結構以單向模態為主，按兩單向SIMO環境激勵模態試驗分析結果更為可靠，尤其是低階模態。從低階模態識別精度、試驗工作量及操作便捷性而言，排架結構模態試驗選擇SIMO單向環境激勵模態試驗優于雙向MIMO法。