軌道長波不平順半測回法測量精度的研究(Ⅰ)

熊麗娟，朱洪濤，王志勇，吳維軍，魏 暉

(1. 南昌大學機電工程學院，江西南昌 330031；2. 南昌航空大學航空制造工程學院，江西南昌 330063；3. 江西科技學院汽車工程學院，江西南昌 330098)

高速鐵路要求軌道幾何狀態保持極高的平順性，否則行車舒適性和安全性將受到影響[1]。實現軌道高平順性是高速鐵路的核心問題之一。

軌道不平順通常指軌道的幾何形狀、尺寸和空間位置相對其正常狀態的偏差，它是機車車輛振動的重要激擾源[2]，直接影響列車運行安全性、平穩性和舒適性[3-4]。按其波長特征可分為短波、中波和長波不平順三類，波長在幾毫米至幾百毫米的不平順稱為短波不平順，波長1～30 m的不平順稱為中波不平順，波長30～200 m的不平順稱為長波不平順[5-6]。

假設車體自振頻率為f(Hz)，當列車以速度v0(km/h)運行時，可能使列車產生共振的線路不平順最不利波長λ=v0/(3.6f) (m)[7-8]。高速列車車體主振頻率多在1 Hz左右[9]，當v0為250 km/h時，最不利波長λ約為70 m；當v0為350 km/h時，最不利波長λ約為100 m。文獻[6，10]都明確顯示，隨著列車運行速度的提高，以往對列車輪軌動力作用影響不明顯的長波不平順逐漸成為影響高速列車運行安全性、平穩性和舒適性的主要因素。因此，高速鐵路線路必須加強對長波不平順的監測。

本文將70 m長波數據(工程上軌道不平順的波長范圍通常為1.5～70 m[11])作為研究對象，在保證工程實用性的前提下分析如何提高長波數據的檢測精度，提出實時補償地球自轉的數學模型，并通過實際線路試驗驗證其有效性。

1 長波數據的測量方法

具體地說，長波數據包括長波軌向數據和長波高低數據。某測點的70 m長波軌向值，是指這個點在鐵路平面曲線上被測得的70 m弦中點弦測值v，如圖1所示；這個測點的70 m長波高低值，是指此點在豎曲線上被測得的70 m弦中點弦測值。

圖1 70 m長波軌向值定義

長波數據屬軌道內部幾何參數，可以通過相對測量得到，亦可通過絕對測量得到，還可通過激光準直技術[12]測得。

相對測量通常使用軌道檢查儀(軌檢儀)，通過測量軌道上每一小段的轉角，用“以小推大”的方法獲得長波數據[13]。其測量效率較高，但“以小推大”容易累積誤差，導致在所測線路上只推行軌檢儀一遍(即半測回法)獲得的長波數據精度偏低。目前相對測量法軌檢儀測長波時，采取在同一段線路上往返推行的方法(一測回法)，將順逆推的兩次數據取平均來消除其共同誤差。一測回法大幅提高了長波數據測量精度，但也降低了工作效率，在鐵路工程上幾乎是個致命缺陷。

絕對測量則是將CPⅢ點作基準，利用全站儀組合軌道測量儀測得軌道上各測點坐標，再通過幾何關系推演長波數據。絕對測量因需使用全站儀照準棱鏡，效率較低，精度易受環境影響。通車路段的天窗時間有限，雖然絕對測量不會產生誤差累積現象，在操作得當情況下長波數據測量精度也較高，但在鐵路工程中使用仍不方便。

利用激光準直技術測量長波的具體方法可參考文獻[12]。它和絕對測量一樣，存在低效和易受環境影響的問題，因此也未推廣。

總結以上可知，若能只推軌檢儀一遍(半測回法)即獲得高精度的長波數據，則以上方法中相對測量法的工程實用性最佳。

2 半測回法長波數據測量精度的影響因素

相對測量時，軌檢儀直接測得每小段線路的轉角，再“以小推大”獲得70 m長波數據。假設測得的是每0.125 m的轉角φi(rad)，則其70 m長波軌向計算公式為

v70=62.5(φ1+2φ2+3φ3+…+279φ279+280φ280
+279φ281+278φ282+…+φ559)

(1)

式中：v70的單位是mm。其他參數如圖2所示。

用式(1)求70 m長波軌向本身就存在系統誤差。由文獻[13]可推知，在半徑為2 000 m(時速200 km以上鐵路的最小圓曲半徑[14])的圓曲線上，按式(1)計算70 m長波軌向的系統誤差僅為0.023 mm。根據文獻[15-16]，70 m長波的經常保養級(即Ⅰ級)容許偏差管理值最小為6 mm，這意味著其測量誤差不得超過3 mm(置信度99%以上)。而上述系統誤差僅為0.023 mm，不到允許測量誤差的1%。因此，式(1)的系統誤差對高速鐵路長波軌向測量精度的影響可忽略不計。

根據式(1)可知，長波軌向的誤差主要來自轉角φi的測量誤差。轉角φi由光纖陀螺儀(FOG)所測的角速度積分而來。當FOG的零漂為0.1°/h時，如果軌檢儀采用正常推行速度1 m/s，那么由FOG測量誤差所帶來的長波軌向中誤差應在0.3 mm以內。以往試驗數據證明，當軌檢儀采用一測回法測量長波數據時，其誤差確實如此；但若采用半測回法，順里程推和逆里程推出的長波數據差異有時可達20 mm以上。如果半測回法的誤差僅來源于FOG的隨機誤差，其順逆推所得的長波結果不應相差這么大。需要仔細考察該差異的來源。

FOG是慣性傳感器，所測得的載體角速度是該載體相對于慣性參照系的角速度，即絕對角速度。軌檢儀停在鐵路上時，在人們看來它是靜止的，角速度應該為0，但FOG測得的卻是地球自轉角速度在其敏感軸上的分量。因此，在軌檢儀開始推行前，FOG有一去零偏過程。這個零偏實際上包括了FOG儀器本身的零偏和軌檢儀起始位置處的地球轉速分量。隨著軌檢儀的推行，其位置不斷變化，被FOG測得的地球轉速分量也不斷變化，因此推行線路上各點的零偏是不同的，但現行軌檢儀對FOG輸出值只是統一減去起點處零偏，這樣在測量過程中各測點的零偏實際并未完全去除，因此造成測量誤差。

假設軌檢儀在圖3所示的線路上用半測回法以1 m/s的正常速度順里程推行，它在0～7這8個測點上因鐵路彎曲而獲得的角速度依次為ω0，ω1，…，ω7，零偏依次為Z0，Z1，…，Z7，那么FOG的實際輸出依次是ω0，ω1+Z1-Z0，…，ω7+Z7-Z0；當軌檢儀逆里程推回時，測點7成為起點，設逆推時0～7各點零偏依次為Z0′，Z1′，…，Z7′，則FOG在0～7點上的實際輸出為-ω0+Z0′-Z7′，-ω1+Z1′-Z7′，-ω2+Z2′-Z7′，…，-ω7。因為軌向高低這些數據有規定的正方向，比如軌向取順里程右轉為正，所以上述FOG在逆推時的輸出為其相反數。

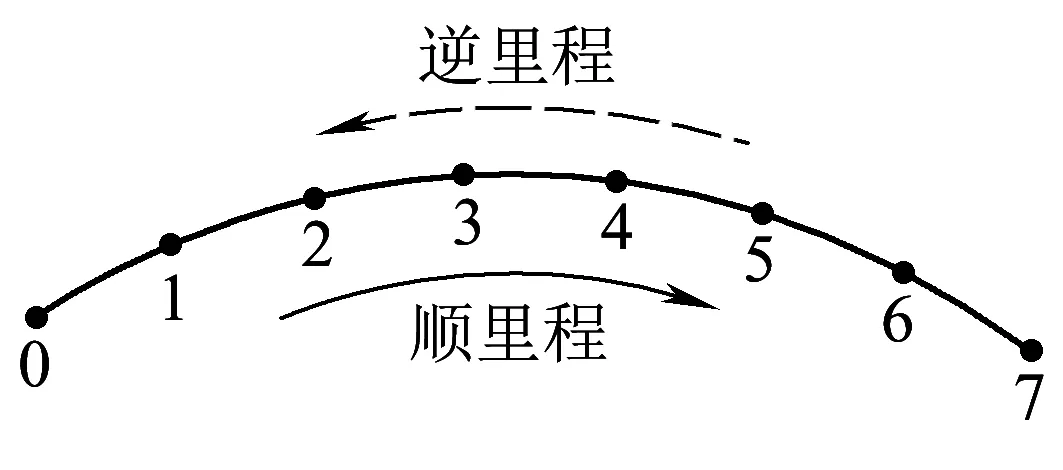
圖3 半測回法線路示意

假設用半測回法順里程推行軌檢儀時，FOG本身的儀器零偏為Za，逆里程時為Za′；在第i個測點處，FOG因地球自轉引起的零偏為Zei(此值順推逆推應一致)，則順推時第i個測點零偏為

Zi=Za+Zei

(2)

逆推時其零偏為

Zi′=Za′+Zei

(3)

在一次測量過程中，儀器本身零偏一般被視作恒定值。但半測回法順推和逆推屬兩次測量，儀器零偏一般會略有不同，因此各測點的順推零偏和逆推零偏使用不同的符號表示。根據式(2)、式(3)，圖3中各測點順推和逆推的FOG輸出見表1。

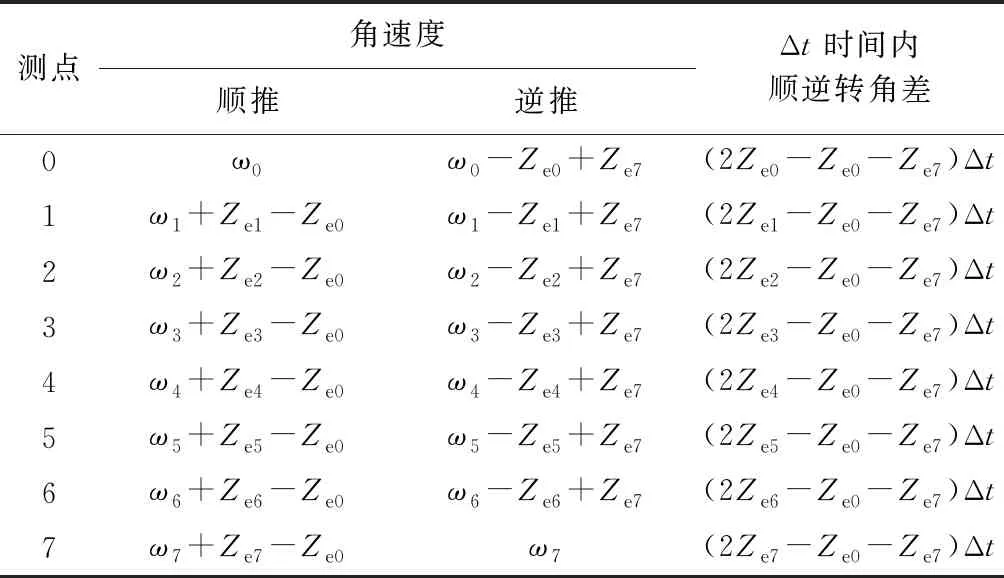
表1 半測回法FOG順逆測量差異

FOG的輸出對時間積分后即得轉角，表1給出了半測回法順推和逆推所得的轉角之差，可以看出該轉角差的變化趨勢與各測點地球自轉分量的變化趨勢一致。推行速度越小，每小段線路花費時間越長，其測出的轉角與真實值的差異越大，順逆推測得的長波數據差異也越大。要減小這種差異，使所測轉角盡量接近真實值(使半測回法的順推和逆推所得長波數據誤差皆在容許范圍內)，需將線路上每點的零偏都正確去除，也可叫作誤差補償。這就是說每個測點的地球自轉分量都需具體算出。

3 地球自轉補償模型的建立

FOG敏感軸上地球自轉分量的計算是建立地球自轉補償數學模型的關鍵。

軌檢儀在軌道上推行的物理模型如圖4所示，軌檢儀外表一般呈T字形，橫梁與鐵軌正交放置，圖4中側臂置于右軌上(也可置于左軌上)。為了測得軌向和高低，其橫梁與側臂交叉處配有兩個單軸FOG。其中，測軌向的FOG盤面平行于軌檢儀車身平面，敏感軸垂直于該平面向下；測高低的FOG盤面垂直于軌檢儀車身平面，敏感軸平行于該平面從左軌指向右軌。現以軌檢儀順里程推行方向為xb方向，高低陀螺敏感軸方向為yb方向，軌向陀螺敏感軸方向為zb方向，建立其載體坐標系。只要將地球自轉角速度在yb和zb方向的分量求出，即可給出高低和軌向陀螺的地球自轉補償數學模型。

地球自轉角速度Ω=7.292 115×10-5rad/s[17]，方向指向地球北極，記其矢量符號為ωie。可以推導出ωie在導航坐標系，即原點位于載體所處位置、坐標軸xn、yn、zn分別指向北、東和垂直向下的坐標系中[18]。

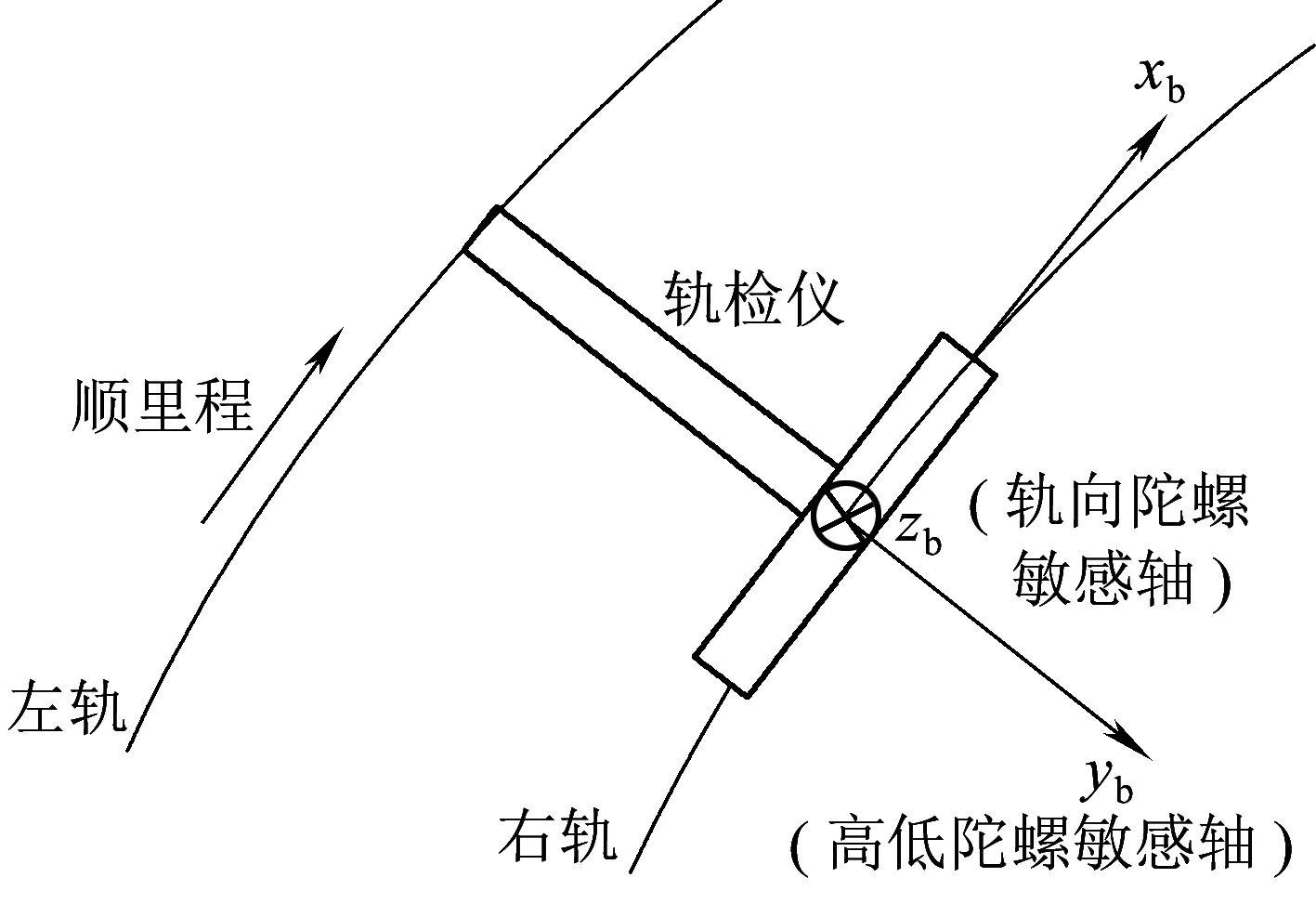
圖4 軌檢儀示意

(4)

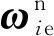
如圖5所示，當載體(此處即軌檢儀)在軌道上所處位置順里程方向的真方位角為A，俯仰角為φ(即軌道坡度角)，橫滾角為Θ(即軌道的超高傾角)時，從導航坐標系到該載體坐標系的變換矩陣為[19]

(5)

圖5 軌檢儀姿態說明

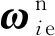
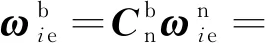
(6)

式(6)矩陣中的第二項即為高低FOG測得的地球自轉分量，可寫作

Zve=
Ω[cosB(sinΘsinφcosA-cosΘsinA)-sinBsinΘcosφ]

(7)

式(6)矩陣中的第三項即為軌向FOG測得的地球自轉分量，可寫作

Zhe=
Ω[cosB(sinΘsinA+cosΘsinφcosA)-sinBcosΘcosφ]

(8)

因此，在第i個測點處高低FOG和軌向FOG的地球自轉補償模型可表示為

(9)

式中：ωvi為高低FOG修正值；ωvi_m為高低FOG直接測得值；Zv0_m為高低FOG在軌檢儀推行起點處測得的零偏；Zve0為高低FOG在軌檢儀推行起點處的地球自轉分量，按式(7)計算；Zvei為高低FOG在第i個測點處的地球自轉分量，按式(7)計算；下標首字符為h的量代表軌向FOG的相應值， 軌向FOG在起點和第i個測點處的地球自轉分量按式(8)計算。

4 試驗結果與分析

由于高速鐵路的實際線形一般與設計線形不會有太大出入，在高低和軌向FOG的地球自轉分量公式中，真方位角A、俯仰角φ和橫滾角Θ擬使用線路設計值。如此，由于地球自轉補償不完全造成的現行長波半測回法順推與逆推之差即可理論預測。

圖6的數據由江西日月明軌檢儀在湯陰至宜溝聯絡線試驗段上采集，它使用現行半測回法在湯宜聯絡線的JD4直線到曲線部分推行，推行里程從4.610 km到5.575 km。

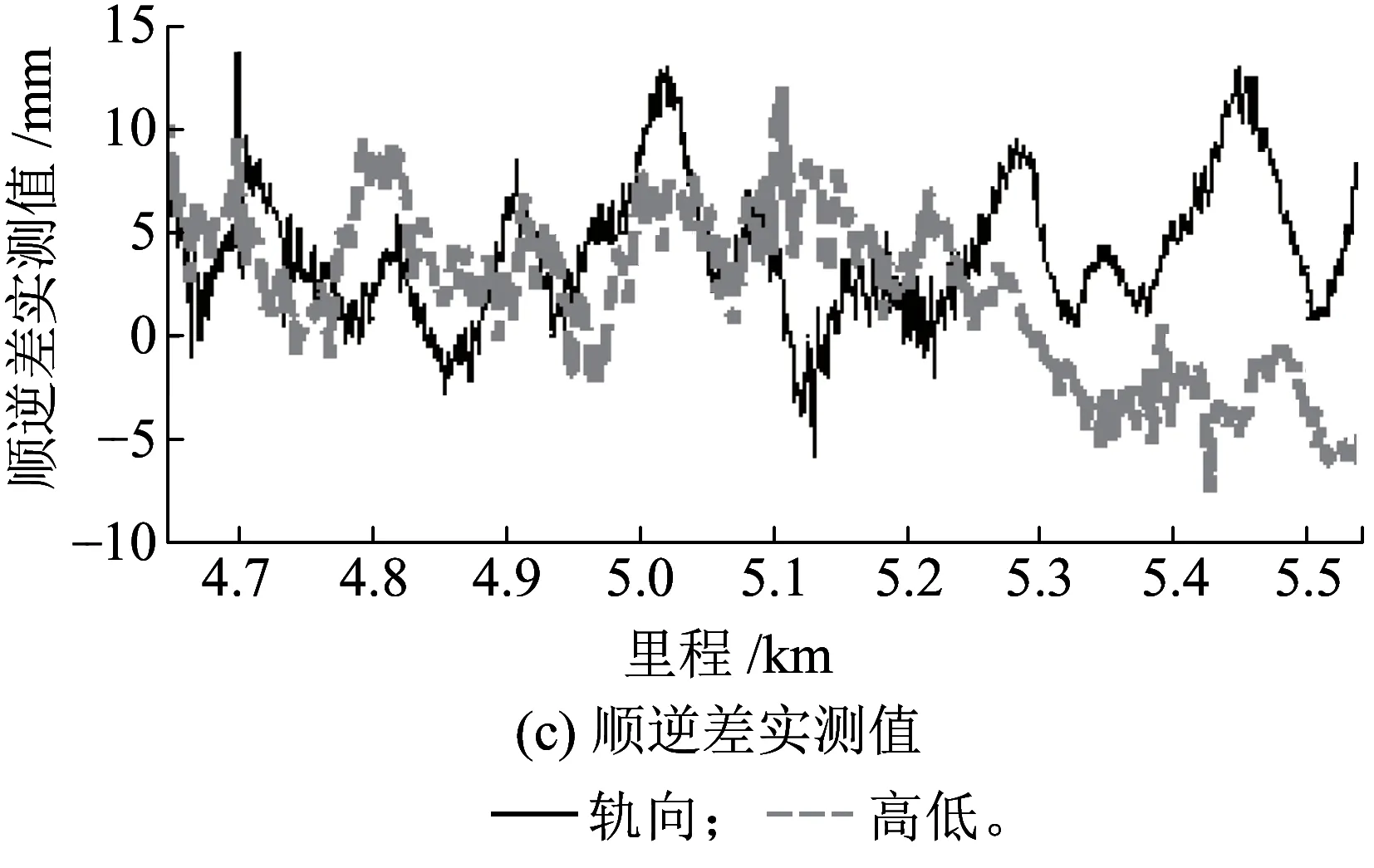
圖6 湯宜線不補償地球自轉之半測回法70 m長波順逆差

從圖6(a)可以看出推行過程中的直線、緩和曲線和圓曲線。圖6(b)給出按照設計資料預測的70 m長波順逆差，圖6(c)為實測的70 m長波順逆差。從圖6可以看出， ，但其趨勢線與預測值之間有5 mm左右的偏移。這種偏差有可能來自起點零偏的測量偏差。它可能源于操作者開機后未待軌檢儀達到溫度平衡即開始作業(由于鐵路工務本身時間上的限制)，也可能源自零偏有效位數取得過少。

總之，由圖6可以看出，半測回法順推和逆推的長波值差異較大(或者說其誤差較大)，不僅有地球自轉未完全補償的原因，還有起點零偏測量不準的原因。將湯宜線半測回法長波數據同其一測回法長波數據(視為相對真值)比較，發現現行半測回法的誤差最大已達到15 mm。

基于上述原因，我們不僅根據式(9)改寫了江西日月明軌檢儀的軟硬件，使其能實時按設計值補償地球自轉，還同時增加了起點零偏測量的有效位數，在昆玉客運專線正線的JD2曲線段上進行了試驗。此次試驗也注意保證了儀器啟動時的預熱時間。

昆玉客運專線正線JD2曲線段總長733.446 m，曲線半徑4 504.548 m，緩和曲線長180 m，曲線右轉，超高45 mm，豎曲線坡度為0。昆玉線70 m長波順逆差預測值與實測值如圖7所示。圖7(a)展示了本段曲線上緩和曲線和圓曲線的位置。

在本次試驗中，軌檢儀推經了JD2整個曲線段。需要說明的是，該軌檢儀上的高低FOG和軌向FOG特意使用了兩種不同精度的光纖陀螺，以了解FOG精度對測量造成的影響。其中，高低FOG零漂指標為不大于0.5°/h(1σ)，軌向FOG零漂指標為不大于0.2°/h(1σ)。在軌檢儀標定過程中也發現，高低FOG的穩定性明顯較軌向FOG差，比例因子變化較大。

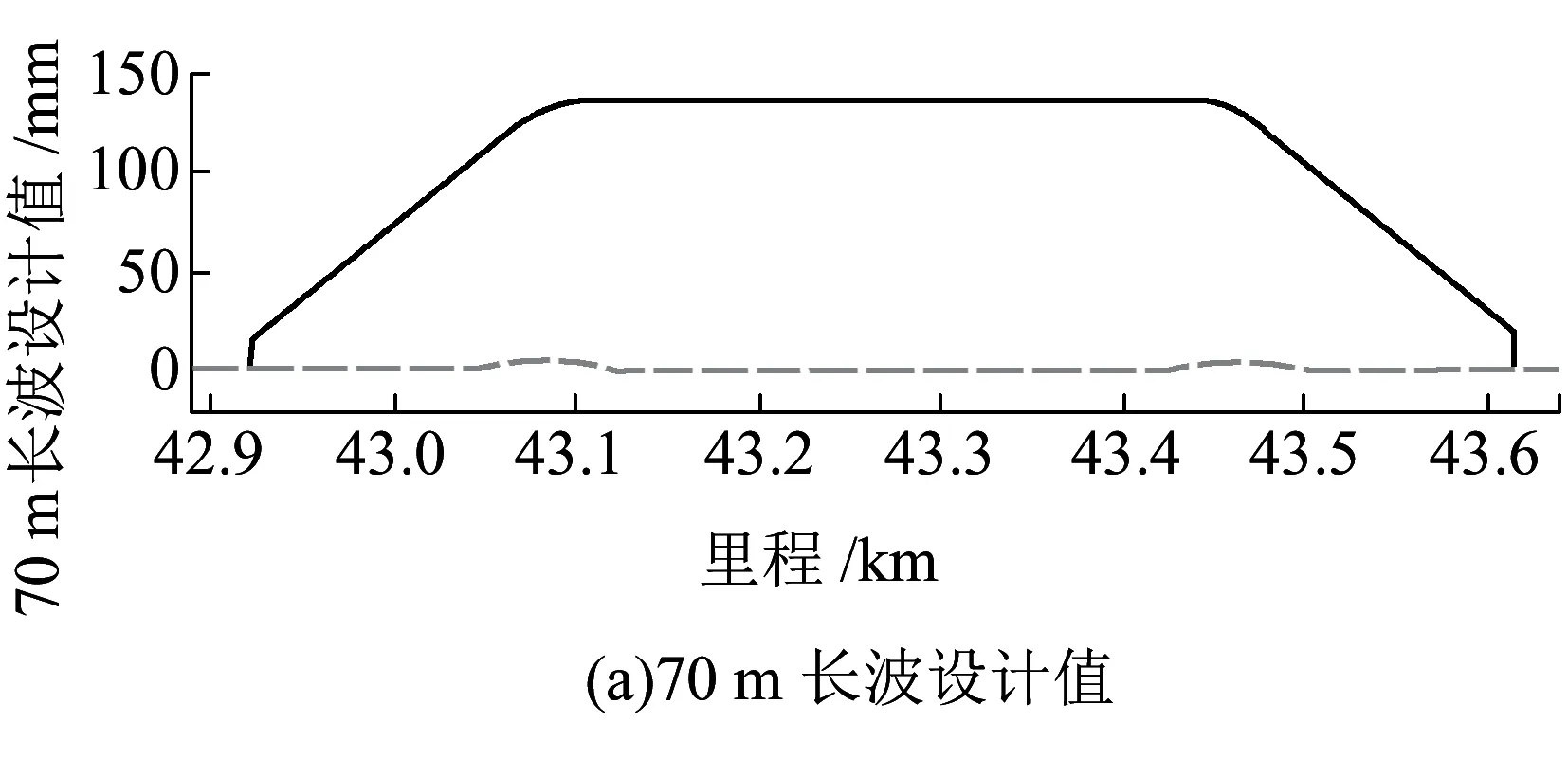
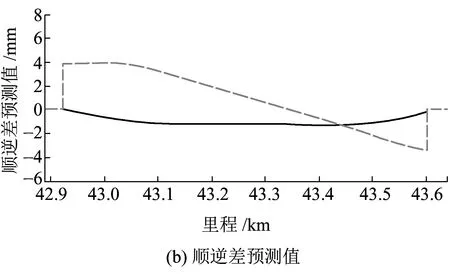
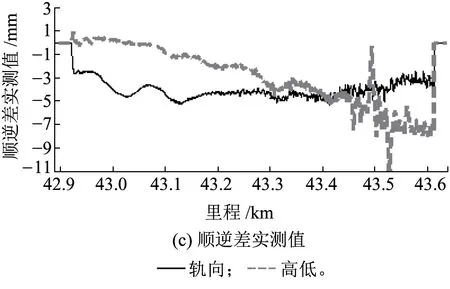
圖7 昆玉線不補償地球自轉之半測回法70 m長波順逆差

圖7(b)、圖7(c)分別給出不補償地球自轉情況下按照設計數據預測的70 m長波順逆差和70 m長波順逆差實測值。由圖7可以看出，預測值與實測值變化趨勢的一致性較高，但是兩者之間還是有一定量的偏移。補償地球自轉之后，70 m長波順逆差試驗結果如圖8所示。

圖8 昆玉線補償地球自轉之半測回法70 m長波順逆差實測值

由圖8可知，地球自轉補償不完全所帶來的順逆差變化已經基本消除；但仍殘留約3 mm的順逆偏差未消除。這可能與硬件在取FOG角速度輸出值時仍然延用了與以前相同的有效位數有關，但從數值上判斷，有效位數問題不會引起高達3 mm的偏移。或是軌檢儀靜置時間過短，起點零偏仍未測準；或軌檢儀靜止和運動時FOG零偏不相同。具體原因留于后續研究探討。

圖7(c)和圖8均為實測長波順逆差，兩圖中高低順逆差曲線均在43.5 km附近出現劇烈波動，而對應的軌向順逆差數據卻比較平緩。這一現象應是由于前面提到的高低FOG精度較低、穩定性較差這一原因引起。也是由于此處的高低波動幅較大，引起了高低FOG的振動，導致粗大誤差的產生。由此可見，FOG的精度不足將會在長波測量中引起令數據失真的較大誤差，這種誤差難以在測量中進行修正，因此用于長波測量的FOG精度必須足夠高。

圖9給出昆玉線一測回法70 m長波數據的均值，以此作為70 m長波的相對真值分別檢驗補償和不補償地球自轉的半測回法長波測量精度。

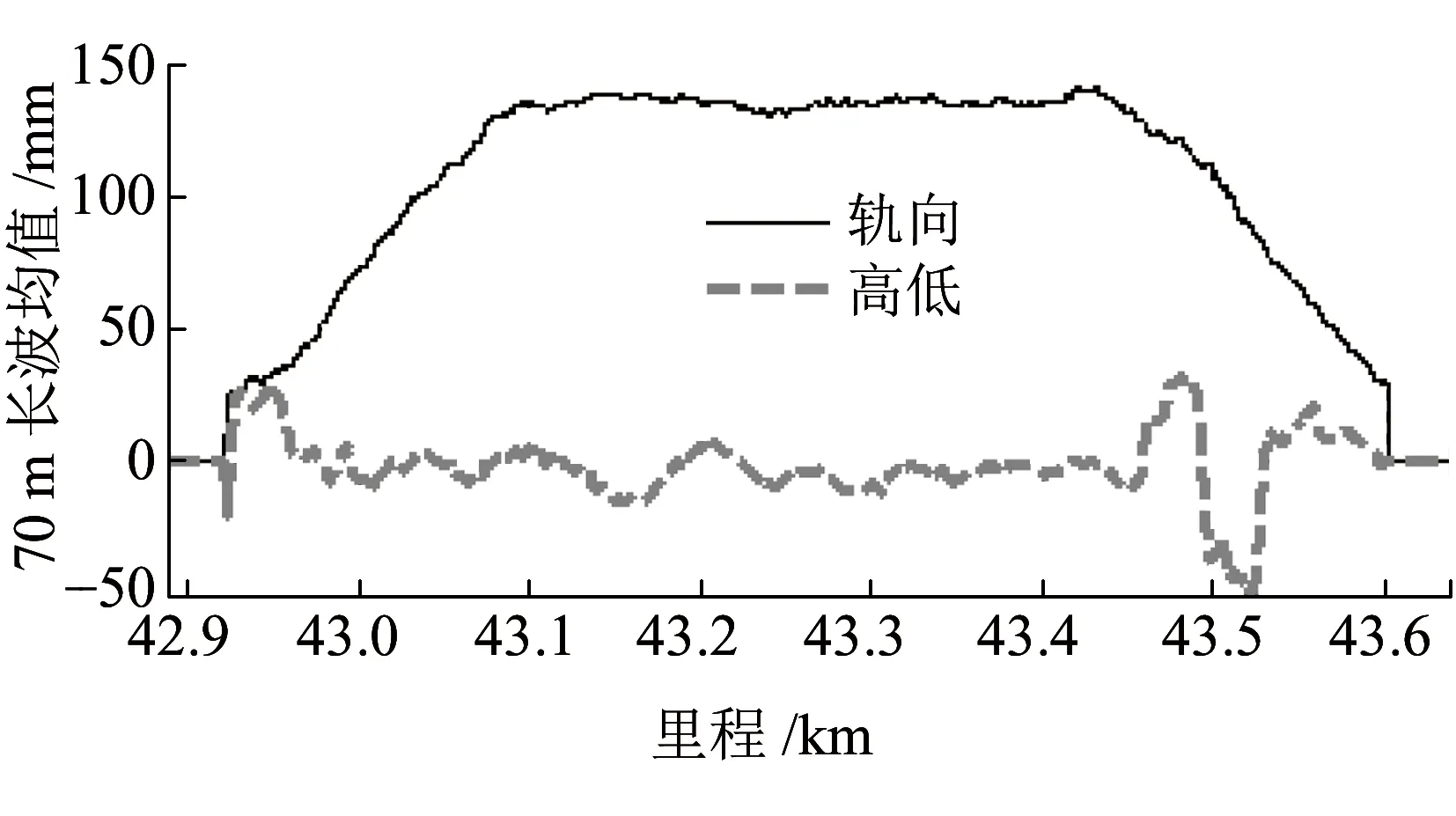
圖9 昆玉線一測回法70 m長波實測均值

圖10為使用不補償地球自轉的半測回法在昆玉線順逆推所測得的長波高低誤差和長波軌向誤差。順逆推的長波軌向誤差基本在3 mm以內，但順推所得的長波高低誤差即使忽略高低FOG精度偏低造成的影響也高達6 mm，不滿足70 m長波不大于3 mm測量誤差的要求。

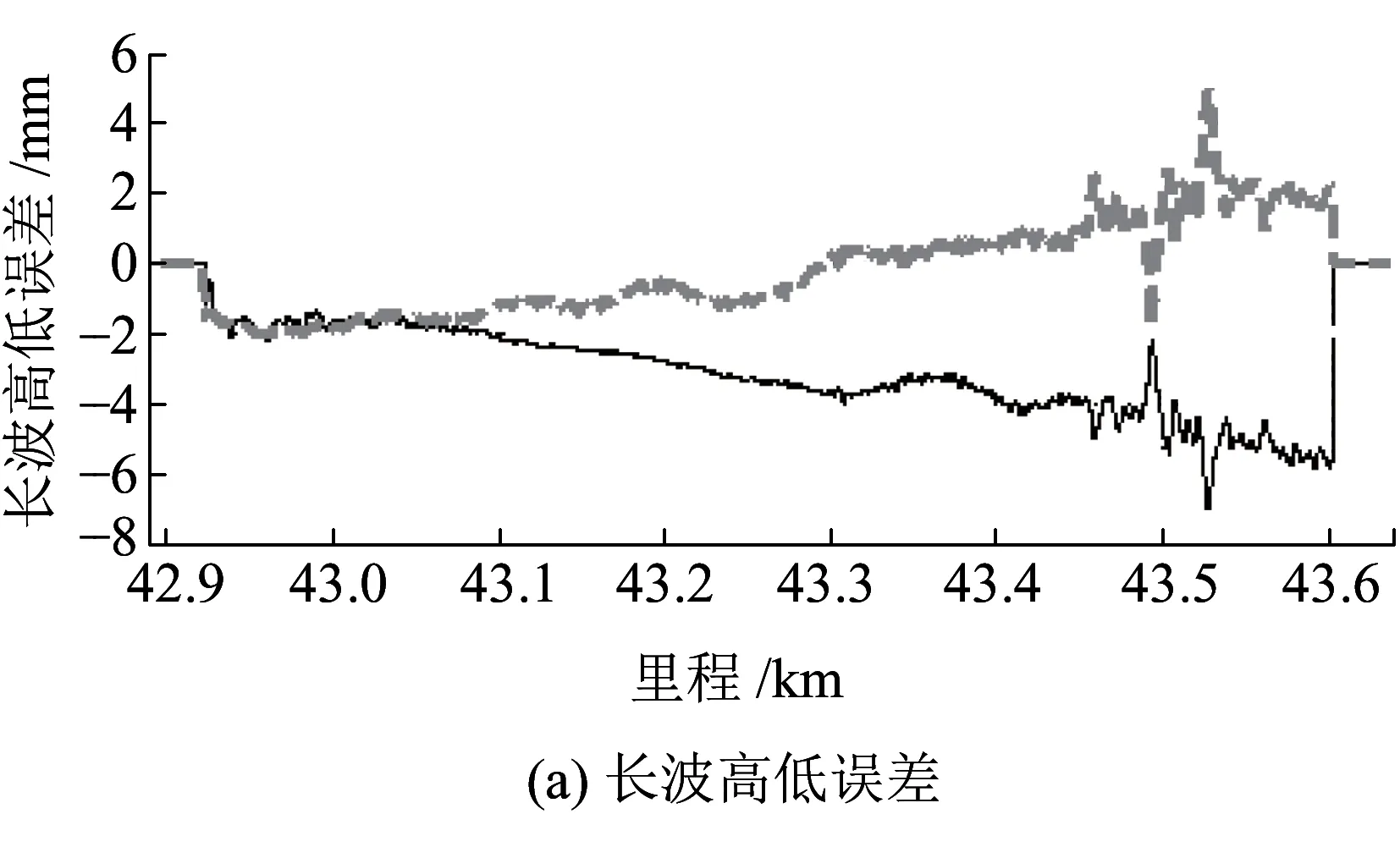
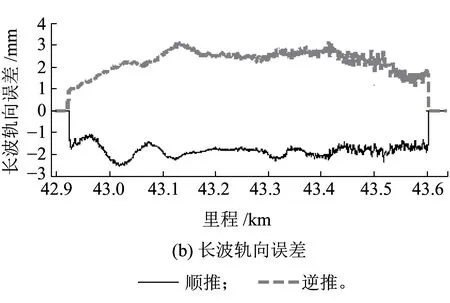
圖10 昆玉線不補償地球自轉之半測回法70 m長波實測誤差

圖11為使用補償了地球自轉的半測回法在昆玉線順逆推所測得的長波高低誤差和長波軌向誤差。若忽略高低FOG在43.5 km附近出現的粗大誤差的影響，則此法順逆推的長波誤差均已在3 mm以內，滿足70 m長波測量誤差不大于3 mm的要求。

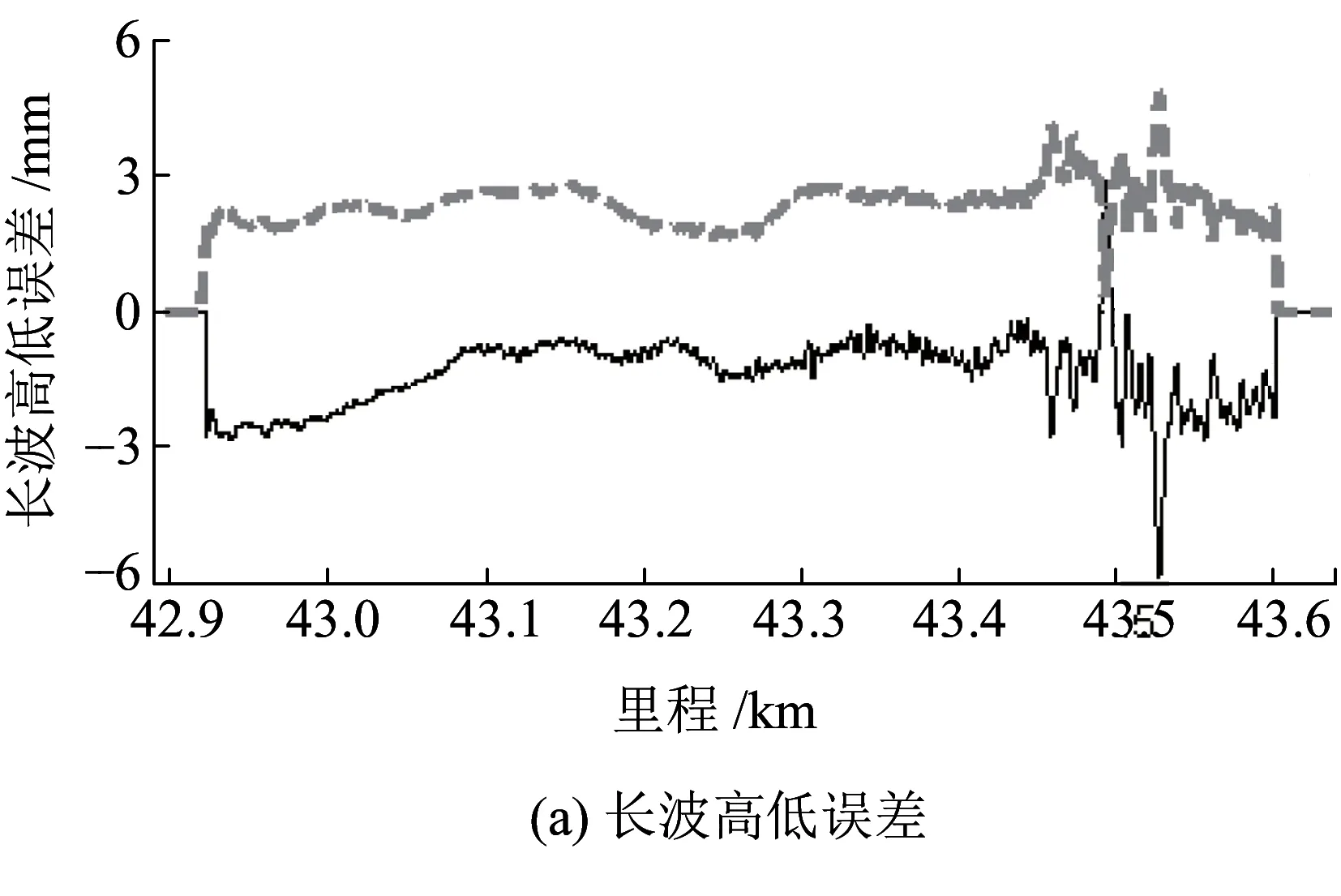
圖11 昆玉線補償地球自轉之半測回法70 m長波實測誤差

綜上可知，在半測回法中對地球自轉分量進行補償能有效提高其長波測量的精度；但在半測回法中依然還有其他影響長波測量精度的因素。這個使長波數據整體發生偏移的誤差，從現象上看應屬于系統誤差，是否能完全消除有待后期研究論證。

5 結論

分析了各種長波測量方法的優劣，認為從工程實用性最佳的角度考慮，應使用相對測量中的半測回法來測取長波數據。但現行半測回法長波精度較低，順逆推的長波結果有時相去甚遠。從理論上分析了半測回法順逆差的來源，認為需將FOG上的地球自轉分量補償完全，才能降低長波順逆差，提高半測回法長波測量精度。

提出了半測回法補償地球自轉的數學模型，通過試驗驗證了該模型的有效性。對真實線路采用現行半測回法測得的長波順逆差，與使用地球自轉分量數學模型根據線路設計資料預測的長波順逆差，其變化趨勢是一致的。

根據建立的地球自轉補償模型，改寫了軌檢儀軟硬件，在真實線路上用補償了地球自轉的半測回法進行長波軌向和高低的測量。發現在提高半測回法長波測量精度上，所建立的地球自轉補償模型的確有效果。雖然此法對精度的提高程度視線路不同各異，但如果FOG精度足夠，其70 m長波誤差值基本能被控制在容許誤差3 mm以內。