基于最大偏差準則的列車衛星定位完好性監測方法
陸德彪, 唐德璋, 蔡伯根,3, 王 劍, 上官偉
(1. 北京市軌道交通電磁兼容與衛星導航工程技術研究中心,北京 100044;2. 北京交通大學電子信息工程學院,北京 100044;3. 北京交通大學軌道交通控制與安全國家重點實驗室,北京 100044)
鐵路作為一種方便快捷的交通工具,是國民經濟發展的“大動脈”,有著運量大、全天候、成本低等優點,是我國最重要的交通運輸方式之一。我國鐵路除了進一步在全國建設高速鐵路,還在加快西部鐵路建設,拓展西部路網,積極優化路網布局,縮小東西部差距,保證我國經濟建設全面、平衡和健康發展。然而我國西部鐵路大多分布在高原、高山等惡劣環境下,運量低,且大部分線路都是單線鐵路,已有的部分線路信號設施不完善。目前鐵路上采用的是固定閉塞制式追蹤列車,即通過應答器、軌道電路和其他軌旁設備結合,實現列車定位、追蹤間隔,需要消耗巨大的建設與維護資源[1]。同時由于鐵路現場實際環境,部分線路難以鋪設大量地面信號設備。
基于衛星定位的列車定位技術可以大量減少軌旁設備,降低基礎設施成本與維護成本,減少鐵路員工的工作量。我國于2006年在青藏鐵路上應用了美國通用電氣公司的增強型列車控制系統ITCS(Incremental Train Control System),采用差分GPS定位結合車輪傳感器、電子地圖實現列車的測速、定位[2]。應用于列車運行控制系統的衛星定位技術及其相關設備,需要滿足鐵路列車運行控制系統的安全性規范和標準。因此,基于衛星定位系統和鐵路電子電氣設備性能評估指標的評估方法,對量化及有效、合理降低基于衛星定位的列車定位功能的安全風險有著重要指導意義。
眾多學者對列車衛星定位的安全評估方法進行了研究。國外方面,文獻[3]對衛星定位在鐵路生命安全領域的應用進行了研究,根據用戶位置誤差與告警閾值的關系建立完好性風險和連續性風險的失效模型,確立了GNSS(Global Navigation Satellite System)質量評價指標與鐵路RAMS指標之間的映射關系。文獻[4]針對EGNOS的完好性風險使用故障樹分析方法進行分解,對不同環境場景下完好性風險進行分配。文獻[5]采用運行場景經驗反饋OEF(Operational Experience Feedback)方法,對基于衛星定位的列車定位方案,在森林、隧道、鐵路路塹和城市四種典型鐵路運行場景下進行RAMS分析。選擇原始數據(偽距、估計位置以及參考位置),并對導致衛星定位功能狀態變化的信息進行預處理,如比較估計位置和真實位置、計算誤差值并與精度閾值進行比較,記錄每次采樣時的系統狀態,最后分析RAMS指標的數值,為研究衛星定位鐵路應用性能評估方法提供了一套分析流程。
國內方面,文獻[6]提出了基于虛擬應答器的GNSS列車安全定位風險分析方法,在安全應用層的實現方法上,分析了GNSS虛擬應答器實現安全層的風險分配,提出了GNSS虛擬應答器的風險指標方法。文獻[7]針對常規接收機自主完好性監測RAIM(Receiver Autonomous Integrity Monitoring)算法,提出了一種北斗列車定位RAIM可用性預測方法。該方法利用北斗導航系統歷書信息和列車運行計劃,對實際行車過程中的完好性狀態進行預測,為列車在途定位完好性監測計算提供先驗信息,確保定位結果能夠滿足應用需求。
完好性監測方法能夠確保衛星定位技術應用于鐵路系統時,在存在故障、異常的情況下及時發出告警,進行隔離。RAIM技術的基礎是1986年LEE[8]提出的距離比較法,算法通過計算觀測值的預測值并與實際值進行比較,進行故障衛星檢測。1988年,PARKINSON等[9]提出最小二乘殘差法,通過對觀測模型狀態量進行最小二乘估計,構造估計值與實際值間誤差的殘差,根據卡方分布的特性計算檢測統計量和檢測閾值,再進行對比判斷是否存在故障衛星。同年STUTRA[10]提出了奇偶矢量法,將觀測矩陣進行QR分解得到奇偶矢量矩陣和奇偶空間矩陣,再將誤差投影在奇偶空間中,構造觀測統計量與閾值進行比較,識別故障衛星。這三種方法被證明是等價的,且在只有一顆故障衛星的情況下監測效果較好[11]。其中,奇偶矢量法的計算更簡便,但由于涉及矩陣的QR分解,算法設計難度較其他兩種方法更高,需要考慮矩陣分解時算法的精度問題。
水平保護級別HPL(Horizontal Protection Level)是指定位過程中允許的最大誤差,反映了系統運行時的位置安全水平。RTCA DO-229標準將水平保護級別定義為統計誤差,確保位置誤差超過給定閾值的概率是在所要求的完好性風險之內。如果計算出的水平保護級別大于給定的告警閾值,那么系統應當在告警時間內生成警告并通知用戶。若水平保護級別未超過告警閾值,則定位信息可用;否則定位信息不可用。最早由LEE[12]提出HPL方法。HPL估計是RAIM的關鍵部分,在識別故障衛星后,計算得到權值,再結合最小可檢測偏差得到最終的水平保護級別估計值。最小可檢測偏差與偽距觀測量標準偏差、衛星可見數、允許的誤警率以及漏警率有關。
在傳統的HPL估計方法之上,部分學者考慮了其他影響因素,提出了新的估計方法。文獻[13]基于最小二乘殘差法的傳統HPL估計方法,考慮了噪聲對水平保護級別計算結果的影響,在計算中加入代表噪聲影響的圓概率誤差,獲得了基于最大水平偏差和噪聲相互作用的HPL估計方法。
對于基于衛星定位的列車定位方案的安全評估,需要按照完整的評估方案,量化相關性能指標,從而保證衛星定位技術在鐵路行業的發展與應用。本文主要針對水平保護級別的量化方法進行研究,提出一種基于最大偏差準則的完好性風險量化方法。在最小二乘殘差法的HPL 估計方法(傳統方法)的基礎之上,考慮了觀測噪聲對水平保護級別的影響,提高水平保護級別計算結果的可信度。
1 衛星定位完好性及鐵路電子設備安全完整性概念
1.1 完好性
GNSS性能評價有四項指標,除完好性之外,還包括精度、連續性和可用性,這四項簡稱為ACAI指標。連續性、可用性和完好性都是建立在精度指標評估方法基礎上的,是其他3個性能指標的基礎。可用性是在長時間下的性能指標,而連續性是特定時間間隔內的平均性能指標,因此連續性和可用性相關,且可用性建立在連續性的基礎之上。完好性則獨立于連續性和可用性,是對衛星定位結果是否可信的評價。四項性能指標之間的關系如圖1所示[14]。
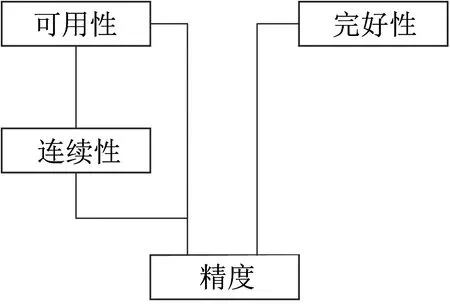
圖1 GNSS的ACAI性能指標間的關系
完好性是評價GNSS性能的重要指標之一,包括了系統向用戶提供及時有效的告警信息的能力[15]。衛星定位系統不會一直處于正常運行的狀態,因此要求能夠在系統出現問題時及時檢測出故障并在可接受的時間范圍內報警。
完好性具體可分為4個特征:告警閾值AL(Alert Limit)、告警時間TTA(Time to Alert)、完好性風險IR(Integrity Risk)和保護級別PL(Protection Level)。本文中主要考慮告警閾值和保護級別,兩者的具體定義為[16]:
告警閾值:安全運行所允許的最大位置誤差,超過閾值系統應及時向用戶發出報警。該參數可進一步分為水平告警閾值HAL(Horizontal Alert Limit)和垂直告警閾值VAL(Vertical Alert Limit)。
保護級別:為保證絕對位置誤差超過所述數值的概率不超過目標完整性風險而計算的統計誤差限界。與告警閾值相似,保護水平可以進一步分為水平保護級別HPL(Horizontal Protection Level)和垂直保護級別VPL(Vertical Protection Level)。
由于列車沿固定線路運行,在鐵路領域通常只考慮水平方向的特征,即水平告警閾值和水平保護級別。
1.2 安全完整性
在鐵路信號領域度量系統服務質量時,通常使用可靠性、可用性、可維護性和安全性四項指標,即鐵路RAMS指標。RAMS指標關系如圖2所示。安全性與可用性之間是相互關聯的,安全性要求和可用性要求的不足可能會妨礙系統的可靠實現。而只有滿足了所有可靠性和可維護性要求,才能實現安全性和可用性目標。
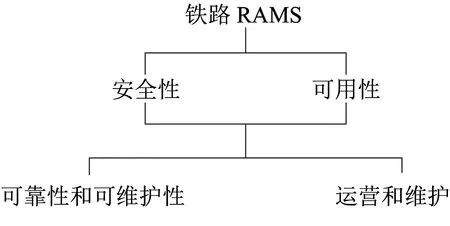
圖2 鐵路RAMS指標關系
根據EN 50126標準[17],安全性定義為免受不可接受的損害風險的能力。為了定量評估鐵路信號系統中的安全性,EN 50129標準[18]對安全性的需求進行了詳細的介紹,定義了安全完整性,并通過安全完整性等級SIL(Safety Integrity Level)描述鐵路安全相關系統的安全目標。安全完整性的定義為:在規定的操作環境和時間內,安全相關系統在所有規定條件下實現其所需安全功能的能力。安全完整性越高,系統無法實現所需安全功能的可能性就越低。而安全完整性等級就是表示系統在系統故障方面滿足其規定安全功能所需置信度的數字。安全完整性分為4個等級,從低到高依次分SIL1、SIL2、SIL3和SIL4[18]。
在EN 50129標準[18]中,系統功能的安全目標被分為定性安全目標和定量安全目標,定性安全目標采用安全完整性等級描述,定量安全目標采用可容忍危險率THR描述,兩者之間通過SIL表進行轉換,見表1。

表1 SIL表
由此可見,對衛星定位鐵路應用進行安全分析時,需要同時考慮GNSS的ACAI指標和鐵路的RAMS指標,并最終按照鐵路安全完整性指標中風險率HR進行評估。風險率的估計,通過衛星定位完好性指標中HPL和HAL之間的關系描述,即HR=p(HPL 水平保護級別指標可以實現系統對定位結果的監測,確保定位結果安全可信。文獻[19]提出了一種計算水平保護級別的新方法,將完好性風險與水平保護級別通過位置誤差的概率聯系起來。這一方法體現了水平保護級別不僅可用于評價定位結果的完好性,還可用于評價定位結果在鐵路應用場景中的安全性。但該計算水平保護級別的方法比較復雜,因此目前計算水平保護級別的方法是基于近似解,并考慮最不利情況下的偏差來進行計算。基于最小二乘殘差法的水平保護級別估計方法是常用的水平保護級別估計方法之一,本文稱之為傳統水平保護級別估計方法。 衛星觀測模型中,偽距觀測模型為 y=Ax+ε (1) 式中:A為衛星觀測矩陣;ε為每顆衛星觀測偽距噪聲組成的向量,服從正態分布。在此基礎上,推出偽距殘差矢量v為 (2) 式中:P-1為觀測噪聲協因數矩陣,A和P-1可以根據傳統衛星觀測模型計算得到,具體計算過程不在此贅述;H=(ATPA)-1ATP;Q=P-1-A(ATPA)-1AT。v中包含有衛星測距誤差的信息,可以用來判斷有無故障衛星。利用偽距偏差向量b是否為0向量判斷衛星是否具有故障,二元假設檢驗為 (3) (4) 此時系統處于正常檢測狀態,若系統告警則認為是誤警。根據給定的誤警率α和χ2(n-4) 的概率密度函數,檢測閾值T可通過式(5)確定。 (5) (6) λ也可以通過給定的漏警率β和非中心卡方分布的概率密度函數確定。 (7) 圖3 統計量概率密度函數 可見衛星數目卡方分布自由度λ6249.987354.468457.769560.5310663.0411767.2412868.8913970.56141072.25 (8) 觀測模型中的偽距誤差δx可以表示為 (9) 因此用戶在水平方向的誤差可以表示為[δEδN]T=[I20](ATPA)-1ATPb,為偽距偏差向量b的函數。水平方向的定位偏差可以表示為 (10) (11) 可將非中心化參數λ代入,結合式(6)和式(11)可得 (12) 本文研究的情況為觀測獨立,且只有一顆衛星存在故障的場景,此時b為一維向量,式(12)可簡化為 (13) D=A(ATPA)-1AT 上述過程推導了偽距偏差向量與最大水平方向定位偏差間的關系,但實際情況中,噪聲也會對水平保護級別產生影響,下面考慮噪聲對水平保護級別的影響。這種噪聲可以通過 (δE,δN) 誤差來描述,這是一種在二維平面內的點位誤差,通過圓概率誤差來描述。本文以天線的真實位置為圓心,水平方向上以r作為包含95%定位結果的圓的半徑,并用r的值衡量噪聲對 (δE,δN) 的影響,記為CEP95,其定義可表示為 (14) 通過式(14)可以計算得到精確的CEP95,但計算過程較復雜,因此通常用式(15)計算。 CEP95=1.227 2(σE+σN) (15) (16) 圖4 基于最大偏差準則的水平保護級別算法流程 通過式(16),得到基于最大偏差準則的水平保護級別計算方法,算法流程如圖4所示。首先讀取接收機輸出的標準NMEA語句中的GPGSV信息來獲取可見衛星數、各可見衛星相對于接收機的仰角和方位角信息。在可見衛星數不低于5個時,利用衛星仰角和方位角信息計算觀測矩陣、觀測誤差協因數矩陣,進而計算HPL值和觀測噪聲的CEP95值,最終得到基于最大偏差準則的HPL值。 可容忍危險率是在對設備或系統進行危險識別和風險分析之后,根據判決結果確定風險率,并與可接受風險進行對比得出的危險失效概率的目標值。可容忍危險率代表對某種危害發生頻率的容忍程度。而危險失效概率的定義是:特定設備或系統上運行的特定安全功能,在特定環境下工作時危害發生頻率。因此有 HR≤THR (17) 把衛星導航應用到鐵路列車運行控制系統當中,作為列車間隔控制和安全包絡估計的基礎條件,需要考慮衛星定位的完好性和鐵路安全相關系統中安全完整性的關系。 將衛星導航系統在用戶端信號接收過程中出現的完好性狀態問題進行分析,分析完好性監測算法在監測過程中出現的誤警、漏警和監測正常共計3個場景下的完好性監測結果的性能。定位誤差未超出告警閾值而由于診斷系統失效發出告警,這種情況稱之為誤警,誤警率與系統的連續性風險有關。而在定位誤差已經超出告警閾值時,系統未發生告警的情況稱為漏警,是系統中最危險的失效,漏警率對應于完好性風險。通過完好性監測結果中的漏警概率進行危險失效率估計,估計的結果作為衛星定位鐵路安全應用的可容忍危險率估計的輸入。 對于應用衛星定位的列車運行控制系統,根據水平定位誤差HPE、水平保護級別HPL和水平告警閾值HAL三者之間的大小關系不同,系統可分為5個不同的狀態,定義如下: (1)系統正常:HPE (2)正常失效:HPE (3)安全漏報:HPL (4)非正常失效:HAL (5)非安全漏報:HPL 圖5為5種狀態下HPL、HPE和HAL之間的關系。 圖5 HPL、HPE、HAL關系對應5種狀態 在衛星定位領域中,一般采用斯坦福圖。以水平定位誤差HPE為橫軸,水平保護級別HPL為縱軸,將每一時刻的定位數據根據這兩個參數打點顯示在圖上,并根據HPL、HPE和HAL三者之間的大小關系將二維平面分割成多個區域,對應不同的系統狀態。通過斯坦福圖,可以清晰地了解到整個試驗過程中系統所處的狀態,確定系統的完整性、可用性等性能。 圖6為斯坦福圖示例,將系統的狀態劃分為5種,對應上面定義的5種系統狀態。根據圖6中落在“非安全漏報”區域的點數,可以對漏警率計算,得到失效率λDU,即危險失效概率HR。在有大量數據驗證的情況下,按照失效率計算方法得到的HR具有普適性,可認為此HR代表了在給定環境場景下衛星定位結果的風險水平。 圖6 斯坦福圖分析方法示例 文獻[20]證明了IEC 61508中提出的每小時危險失效概率PFH與鐵路電子電氣設備的可容忍風險率的表述內涵與外延在鐵路行業應用中等效。文獻[21]認為,在1 h的時間間隔內,PFH約等于HR,HR為發生危險未檢測失效的概率λDU。而危險未檢測失效概率應對應于完好性風險[3]。因此,本文認為衛星導航ACAI性能指標體系中IR的概念等同于鐵路安全相關應用RAMS中HR的概念。HR作為一種失效類型,表示為 (18) 式中:R(t)為系統的可靠性;f(t)為系統發生衛星定位功能發生完好性風險失效的概率密度函數。HR(t)·Δt代表在給定時間間隔(0,t)內系統沒有發生故障的情況下,系統在時間間隔(t,t+Δt)內發生故障的概率。在系統可靠性非常高的情況下,可以認為R(t) = 1。 每小時的HR為 (19) 式中:Pf為危險未檢測完好性監測失效概率;Δt為失效檢測時間間隔。例如,根據Galileo生命安全服務中空間信號性能要求給出的參考數據,在任何時間間隔Δt=150 s內都應有Pf=2×10-7,通過時間擴展方法,可以計算每小時的HR為[22] (20) 為驗證本文提出的基于最大偏差準則的水平保護級別算法,分別使用靜態環境和動態環境下的數據進行驗證。靜態環境數據來源于格爾木架設的基站使用K501采集的數據,動態環境數據為青藏線拉薩至日喀則沿線通過車載的和芯星通UB370接收機和 SPAN IMU-FSAS 系統采集的定位數據。UB370用于獲取定位結果作為估計位置,SPAN IMU-FSAS系統提供原始GPS數據和IMU數據,并能夠通過內置的融合算法生成精度更高的定位結果,因此將該系統輸出的定位結果作為UB370時間測量結果的參考。 試驗過程中,將接收機輸出的定位結果作為估計位置,與參考位置進行比較,計算兩者之間的誤差值。該誤差值用于初步判斷系統在試驗過程中的狀態,作為后續進行傳統水平保護級別估計算法和基于最大偏差準則的水平保護級別估計算法比較使用的參數,用于評估在整個試驗過程中的狀態分布。 圖7為采集動態環境下數據時所使用的SPAN IMU-FSAS參考系統和UB370接收機被測系統,圖8為試驗線路的軌跡。 圖7 SPAN IMU-FSAS系統和UB370接收機測量設備 圖8 拉薩—日喀則線路軌跡 算法驗證所采用的靜態數據為2015年1月27日在格爾木架設的基站K501接收機的結果,輸出頻率為1 Hz,總數據量為18 029。動態數據為2019年1月1日從拉薩—日喀則全線,UB370和 SPAN IMU-FSAS 的結果,輸出頻率為10 Hz,總數據量為74 188。數據基本信息見表3。 表3 算法驗證數據基本信息 整個試驗過程中,各個數據點處水平誤差如圖9所示,靜態環境下水平定位誤差平均值為1.42 m,但波動較大,試驗期間系統定位性能一般;動態環境下水平定位誤差平均值為1.21 m,試驗期間系統的定位性能良好。只有極少數數據點誤差達到了數百米,通過粗大誤差剔除方法進行剔除,本文使用萊以特準則,即以貝塞爾公式計算的標準差下,動態環境測量過程中出現大于3σ的殘余誤差測量值。圖10和圖11分別為試驗過程中靜態環境下的可見衛星數和HDOP值變化趨勢。靜態環境下,可見衛星數較多,但從HDOP變化趨勢來看,衛星的幾何布局不佳,定位結果誤差較大;動態環境下,HDOP略優于靜態環境,因此定位效果略優于靜態環境。 圖9 靜態和動態運行環境下定位誤差結果比較 圖10 靜態環境下的可見衛星數與HDOP值 圖11 動態運行環境下的可見衛星數與HDOP值 對接收機輸出的定位數據幀進行提取,使用在基站處測得的數據計算得到傳統水平保護級別值和基于最大偏差準則的水平保護級別值,如圖12所示。傳統算法的HPL最大值為25.35 m,最小值為14.01 m,最終計算得到的基于最大偏差準則的HPL最大值為40.01 m、最小值為27.23 m。靜態環境測得可見衛星數與HDOP值變化趨勢表明:造成HPL值偏大的原因主要在于部分時間基站所處環境較差,衛星的幾何布局不佳。 圖12 靜態環境下HPL計算結果 對沿線列車基于傳統算法的HPL、噪聲造成的誤差以及基于最大偏差準則的HPL進行計算,計算結果如圖13所示。傳統算法的HPL最大值為38.22 m、最小值為7.79 m,最終計算得到的基于最大偏差的HPL最大值為32.37 m、最小值為19.94 m,符合鐵路GNSS應用需求中低密度線路場景下HPL不超過告警閾值的最大值50 m的要求。由于考慮了測量噪聲對HPL的影響,本文提出的方法計算出的HPL值大于傳統HPL值,誤差趨勢一致。 圖13 動態環境下HPL計算結果 斯坦福圖的告警閾值一般設置為固定值,本文按照低密度線路的告警閾值取50 m。圖14和圖15為靜態環境下使用傳統水平保護級別方法、基于最大偏差準則的水平保護級別方法得到的HPL值進行斯坦福圖分析的結果。可以發現,使用基于最大偏差準則的HPL值會導致定位功能更多地處于“系統正常”狀態,但HPL值也更接近告警閾值。該方法提升了定位功能的完好性,但也可能對其可用性造成一定影響。 圖14 靜態環境下傳統HPL斯坦福圖 圖15 靜態環境下基于最大偏差準則的HPL斯坦福圖 動態環境中獲得的定位數據存在粗大誤差,未經粗大誤差剔除,有95個數據點落在“非安全漏報”區域內,即定位誤差超過告警閾值而不能被診斷系統檢測到,對應于完好性風險。根據落在這一區域中的數據點個數,可以確定整個試驗過程中系統的危險失效概率HR,對應衛星導航ACAI性能指標體系中的完好性風險概率。根據式(19)計算HR為 (21) 動態測試過程中拉日線的HR為6.2×10-4h-1。這是因為衛星定位的結果易受環境影響出現誤差,極端環境下出現易被發現和剔除的粗大誤差,因此通過相應的場景分類方法進行定位場景分類,并按照場景分別分析各個場景下的HR水平。在實際應用中,為降低危險失效概率,通常使用組合定位技術,利用多種傳感器,如多普勒雷達、IMU、ODO、電子地圖,來提高定位結果的精度,保證定位功能在鐵路不同運行環境中的可用性,增強其安全完整性。 去除粗大誤差后,動態環境下使用傳統HPL值和基于最大偏差準則的HPL得到的斯坦福圖分別如圖16和圖17所示。在整個試驗過程中,沒有數據點落在“正常失效”或“非正常失效”的區域內,可以確定定位功能在動態測量的過程中未出現完好性風險,測量結果滿足可容忍風險率10-9≤HR<10-8的要求,達到SIL4水平。 圖16 動態環境下使用傳統HPL值得到的斯坦福圖 圖17 動態環境下基于最大偏差準則的HPL斯坦福圖 圖17中落在“安全漏報”區域的數據點少于圖16中的數據點,這是因為基于最大偏差的HPL值考慮了噪聲帶來的影響,因此計算得到的HPL值更大,可靠性更高。從圖16和圖17的對比中也可以看出,基于最大偏差準則的HPL值計算方法能夠提高系統的完好性,同時對定位功能的可用性有一定影響。 以基于衛星定位鐵路安全應用的安全風險評估為背景,分析了衛星導航領域和鐵路領域既有性能指標中安全相關指標的內涵與外延,確立衛星定位完好性與鐵路電子設備安全完整性概念中相關指標的關系,將水平保護距離的估計方法作為進行衛星定位鐵路應用安全分析的直接量化參數,提出了一種基于最大偏差準則的衛星定位完好性風險量化方法。 本文所述的基于最大偏差準則的水平保護級別估計方法與傳統基于最小二乘法的水平保護級別方法相比,所具有的優勢主要體現在兩個方面:在水平保護級別估計結果的準確性方面,所述的方法能夠有效確立列車位置解算過程中的最大水平方向定位偏差,為列控系統中進行列車安全定位所需的安全包絡估計提供數據來源;在基于HPL和HAL比較的風險率計算方法方面,所述的方法能夠有效地結合衛星定位結果誤差、保護距離和告警閾值三者比較的結果和鐵路可容忍風險率之間的關系,進行風險量化評估,并通過斯坦福圖建立定位狀態和風險之間的關系。計算結果表明基于最大偏差準則的完好性監測算法能夠有效保障定位結果的完好性和安全完整性,降低出現非安全漏報的風險。 在后續研究中,將進一步關注在不同列車衛星定位的環境場景下的風險水平,完善列車運行場景和環境場景等需求下的風險量化方法,實現列車所處的環境、車載定位設備出現定位結果完好性監測問題的故障處理方法,提升算法的適應性。2 水平保護級別估計方法
2.1 傳統水平保護級別估計方法
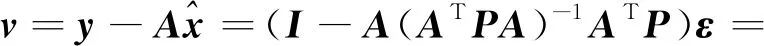
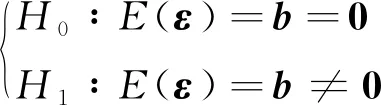


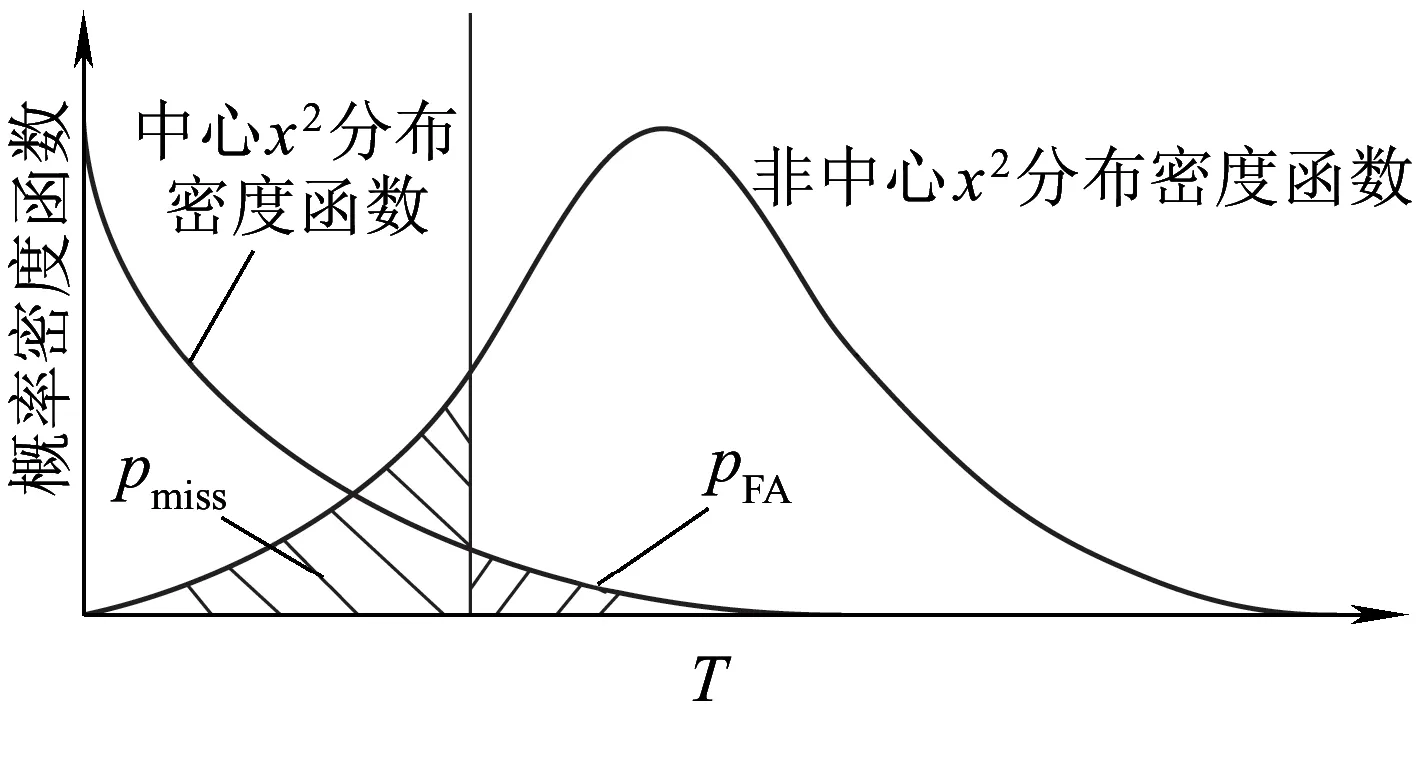
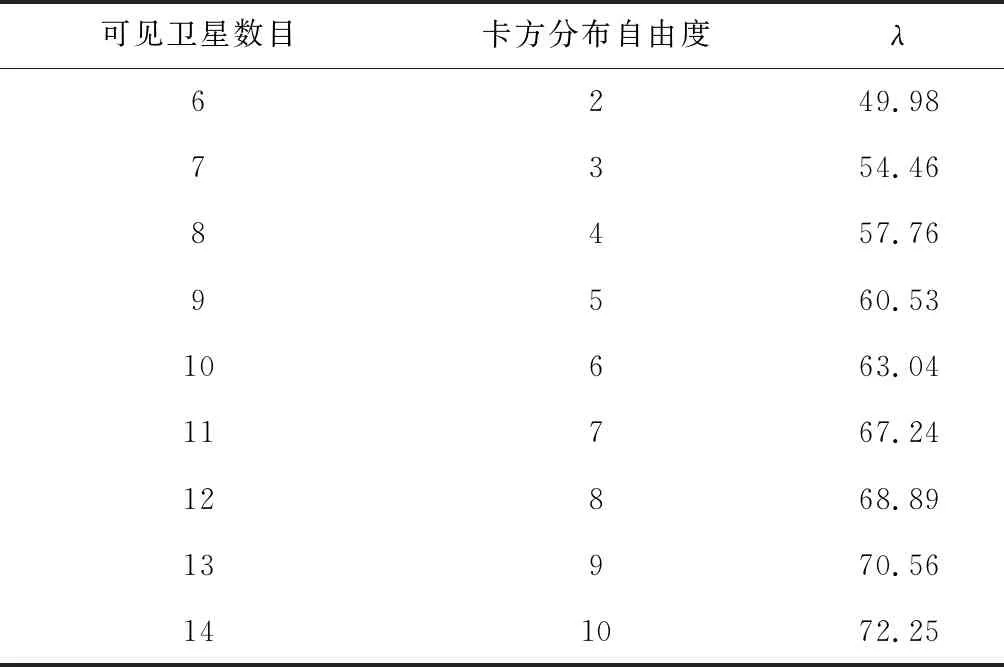
2.2 基于最大偏差準則的水平保護級別算法
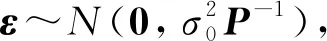
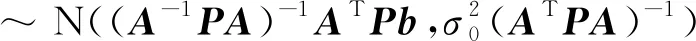

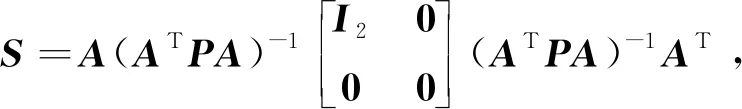
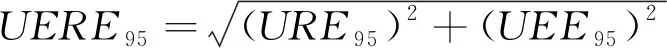
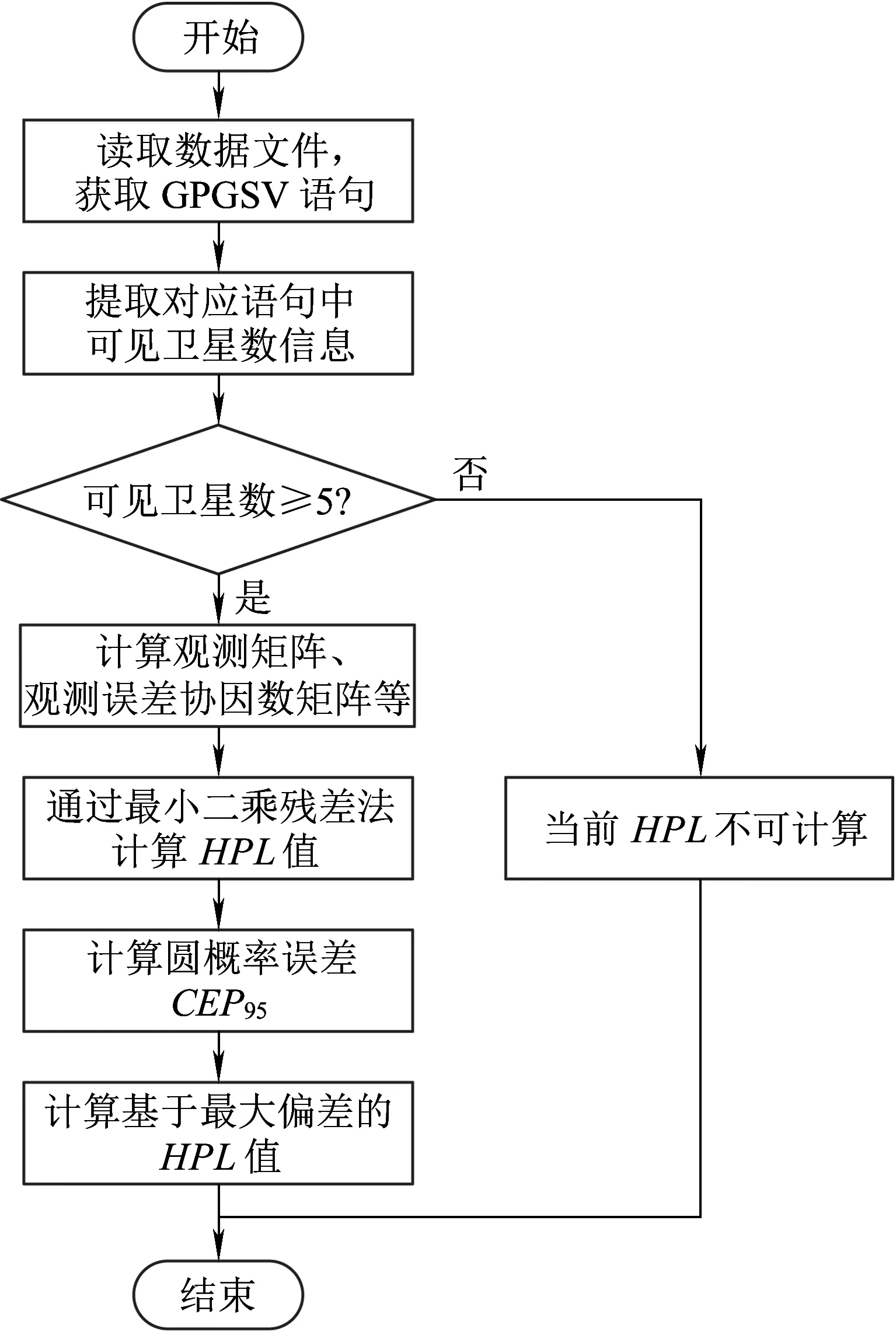
2.3 危險失效概率計算方法
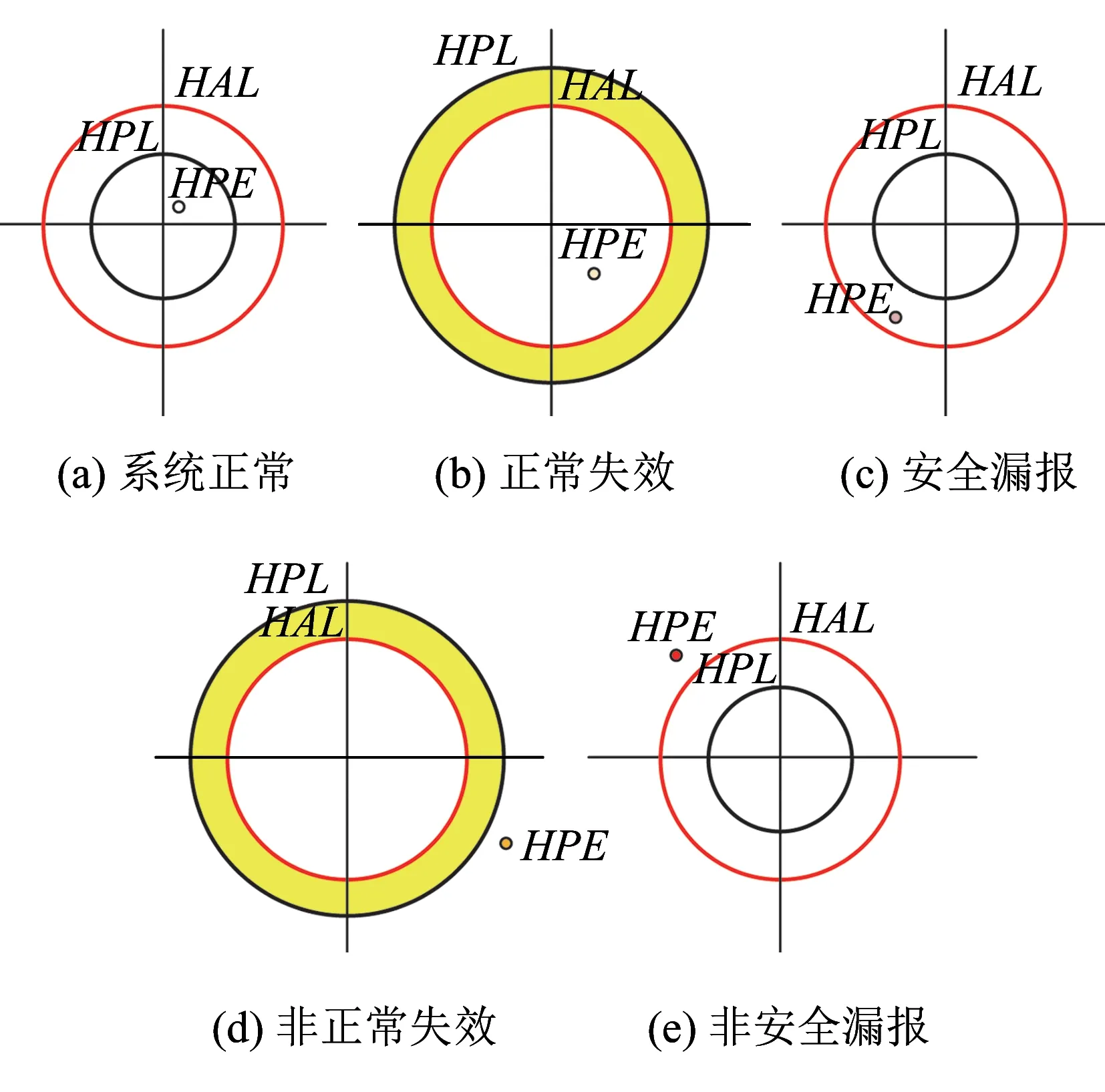
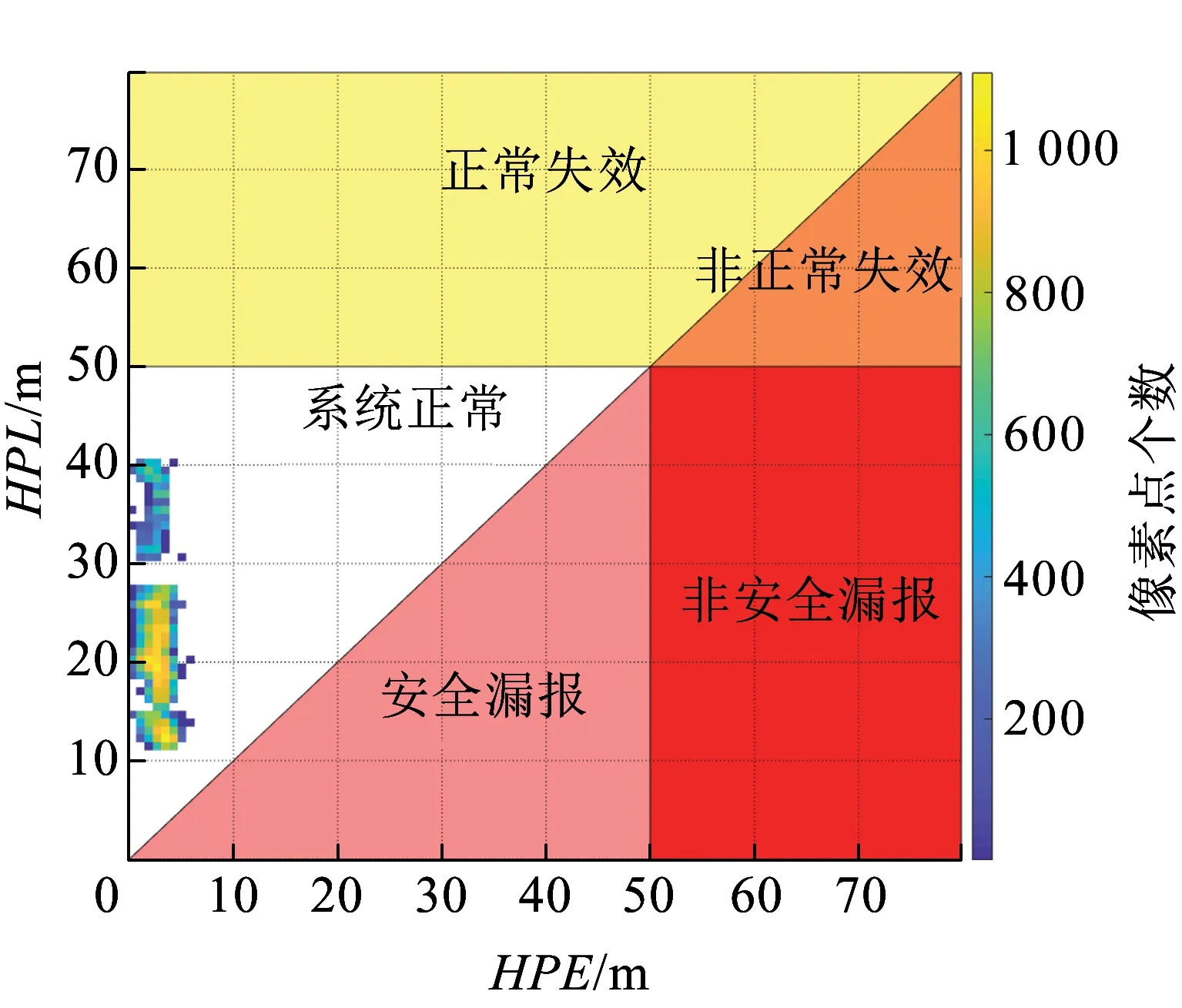
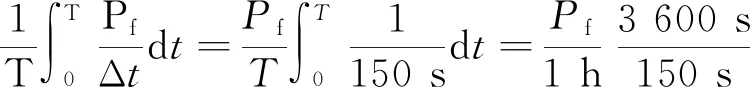
3 算法驗證與評估
3.1 驗證環境及方案

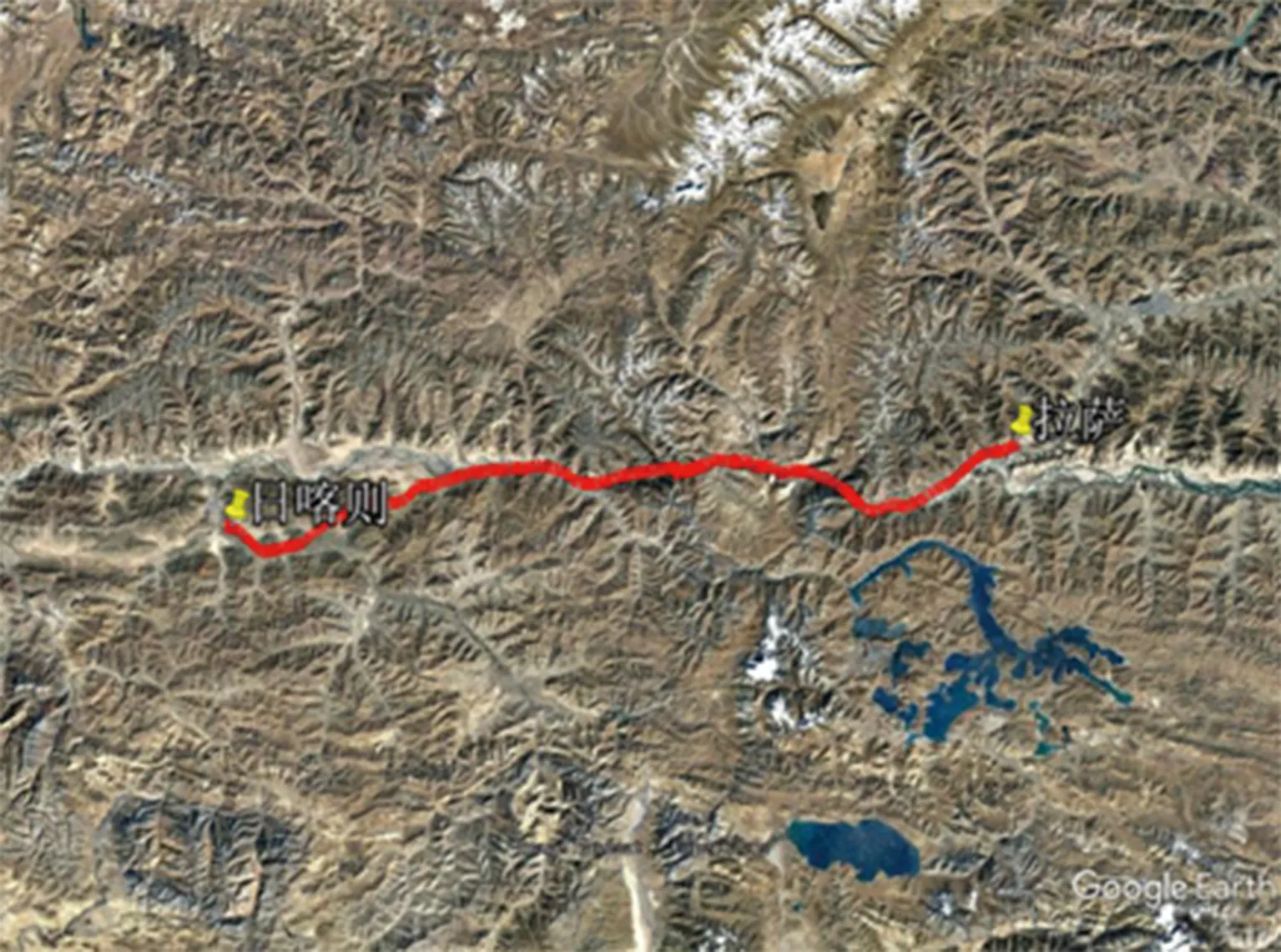

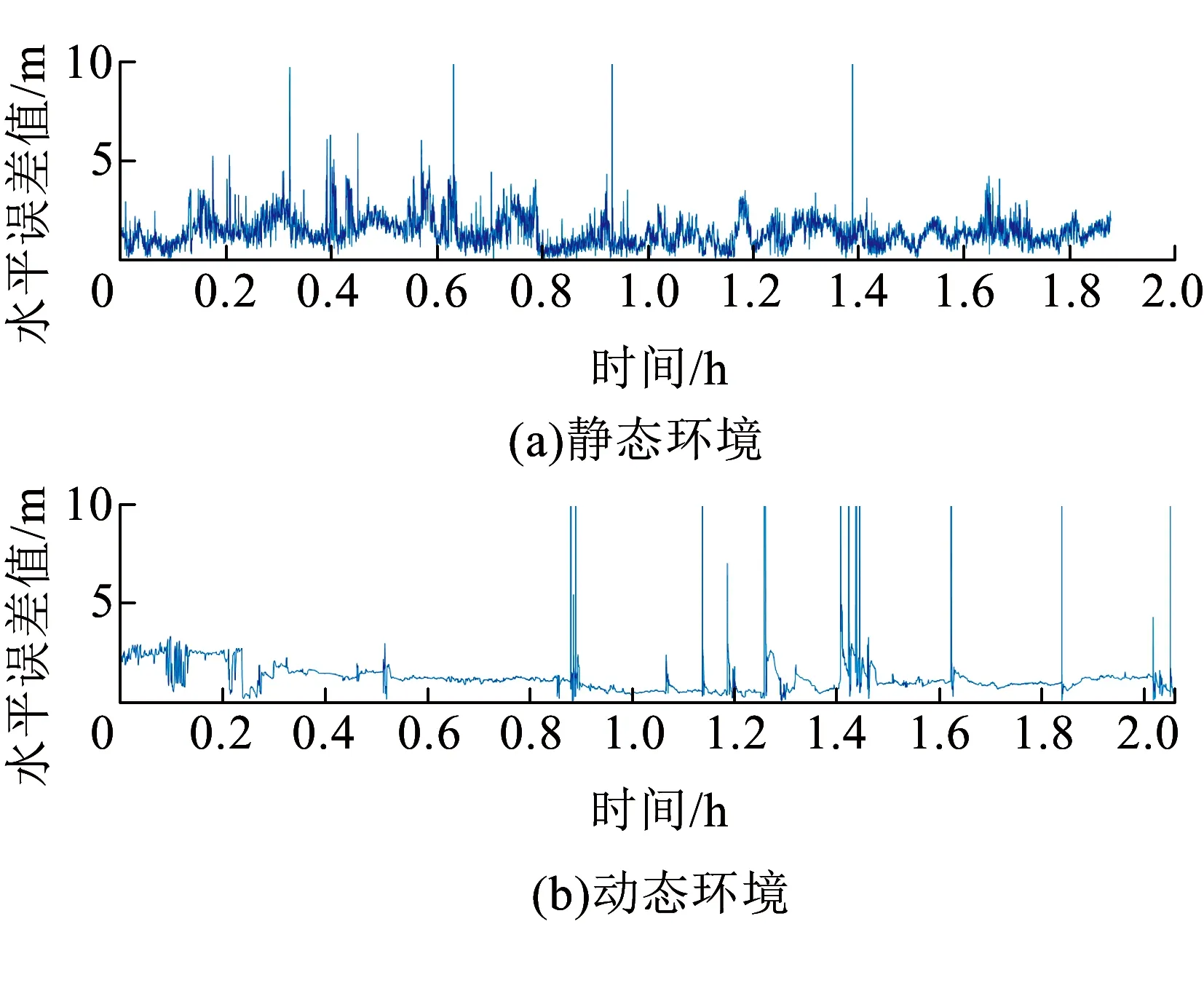

3.2 水平保護級別估計
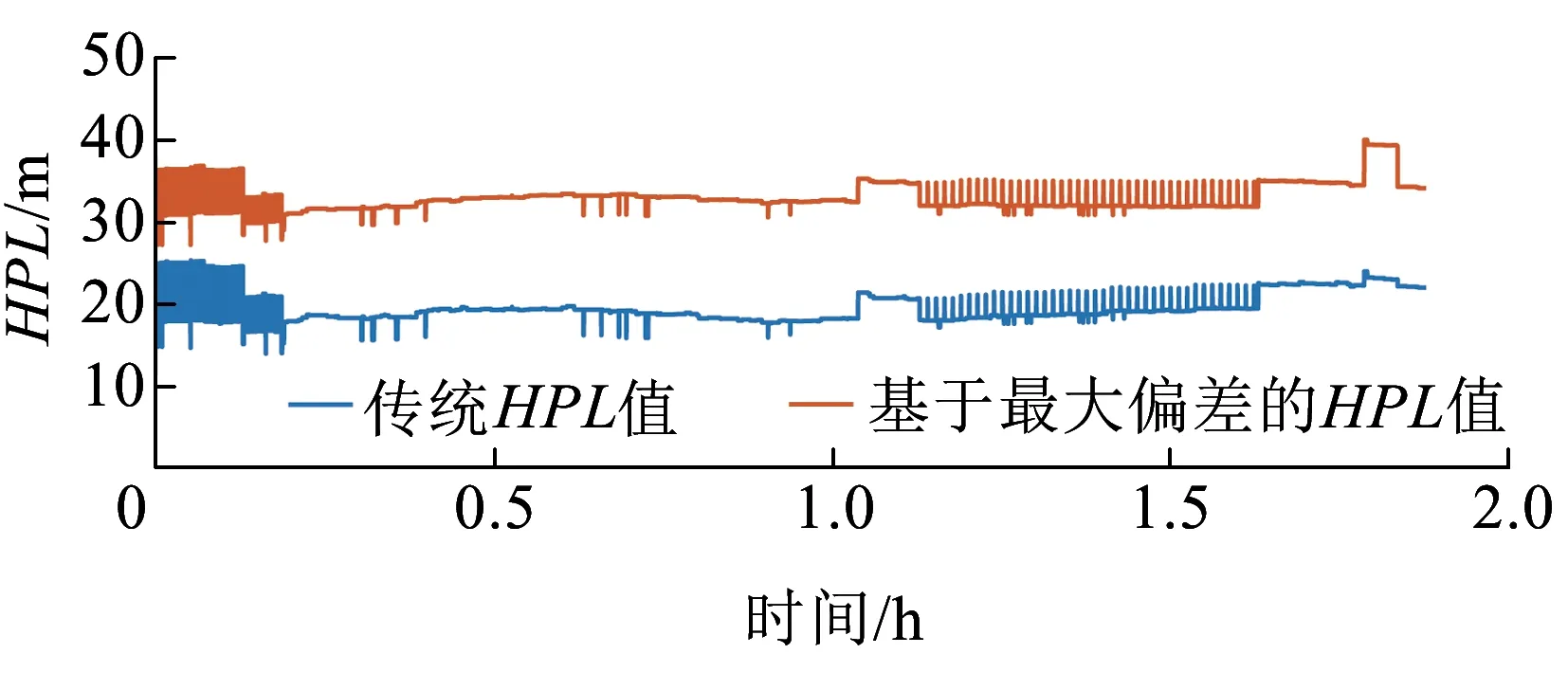
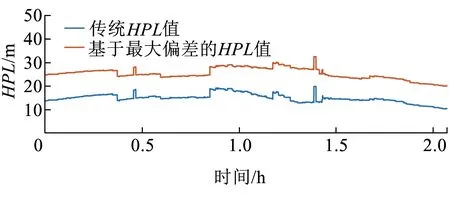
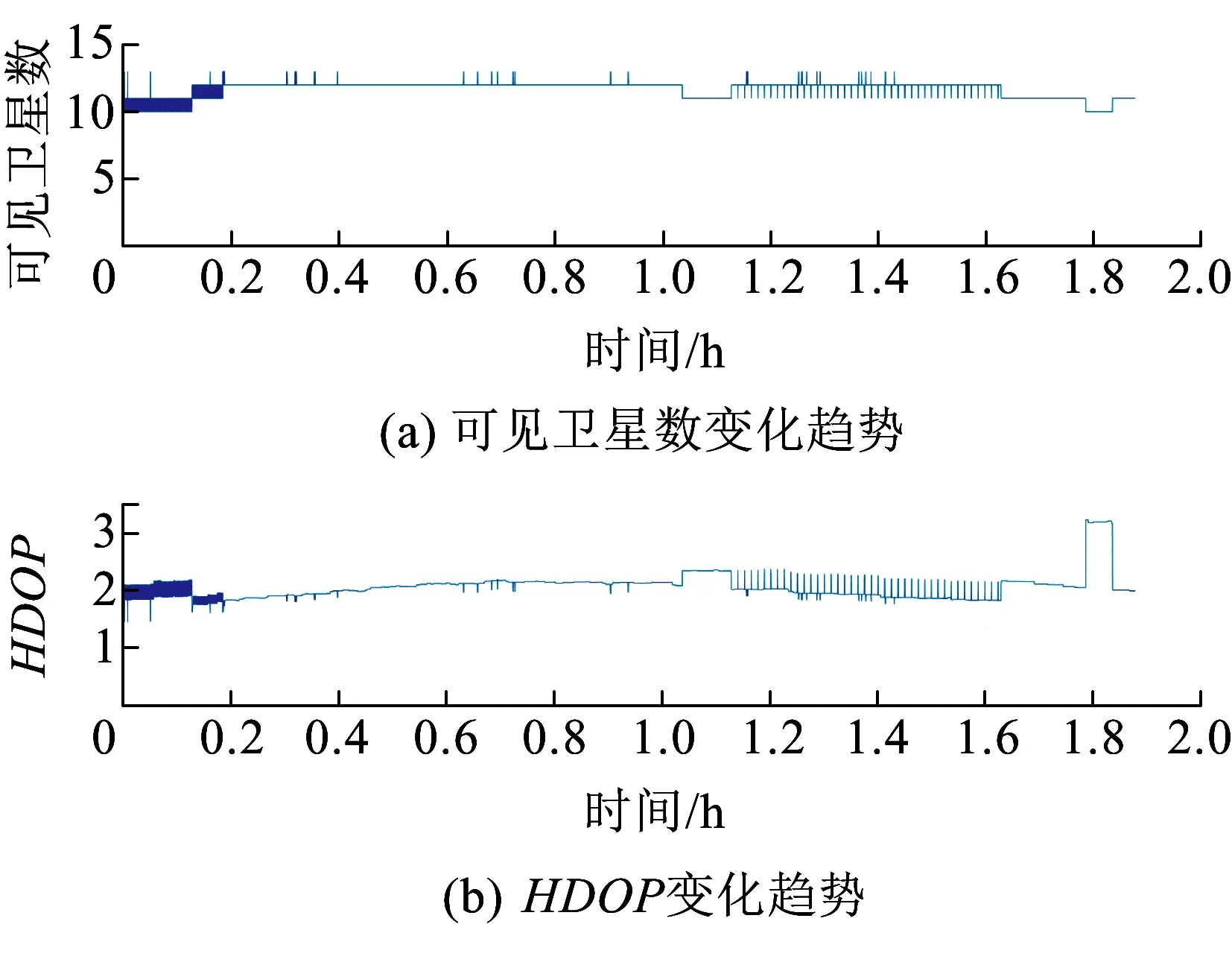
3.3 定位功能狀態評估

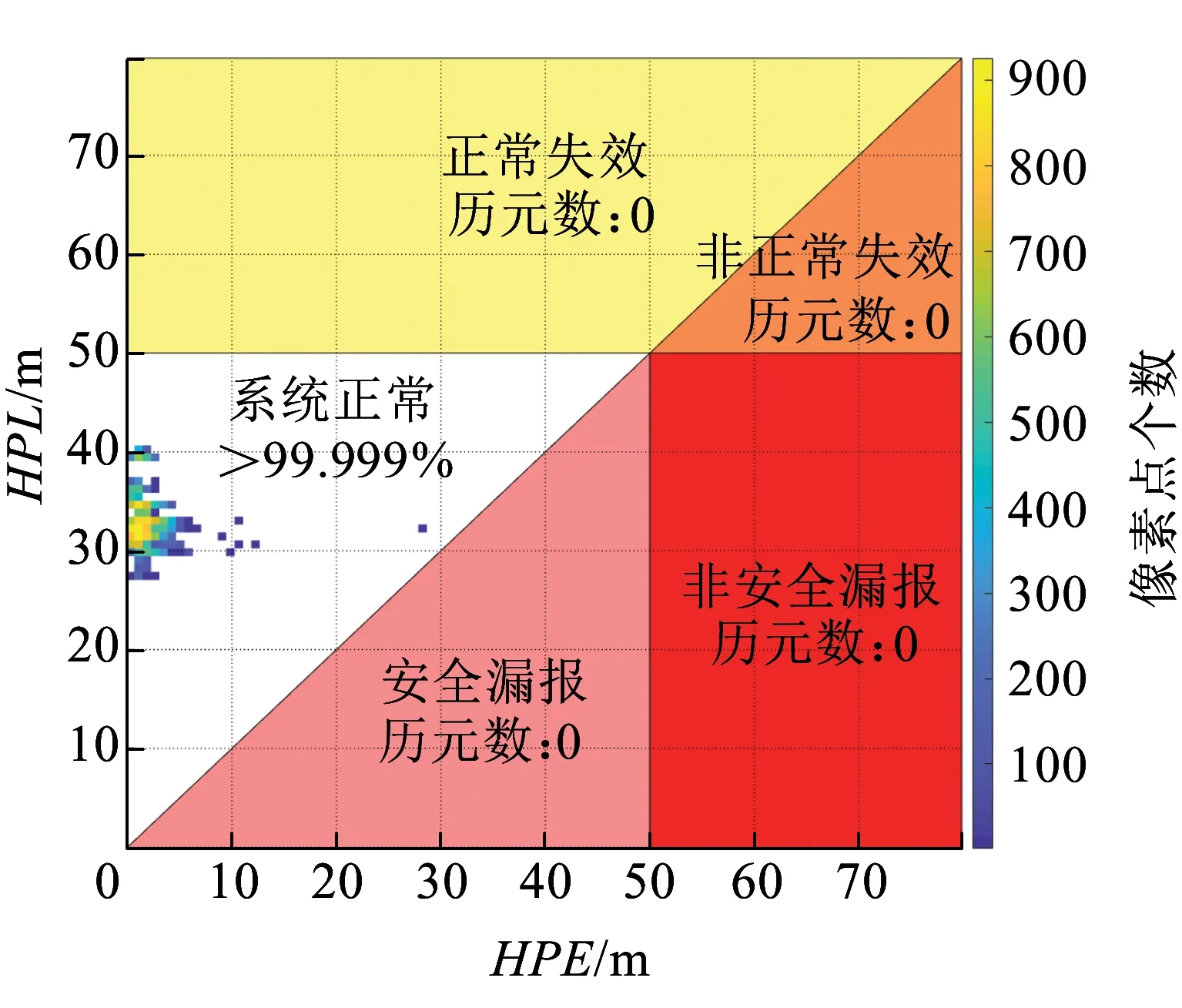
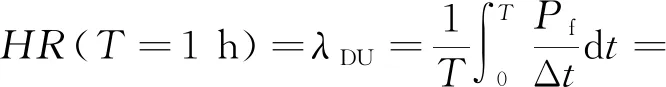
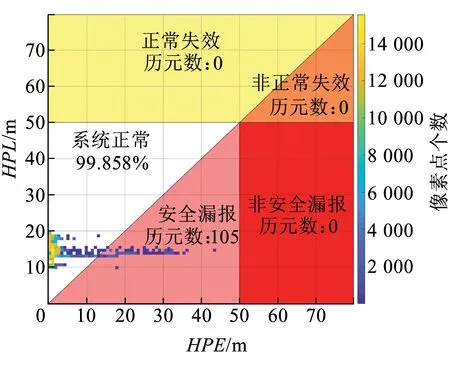
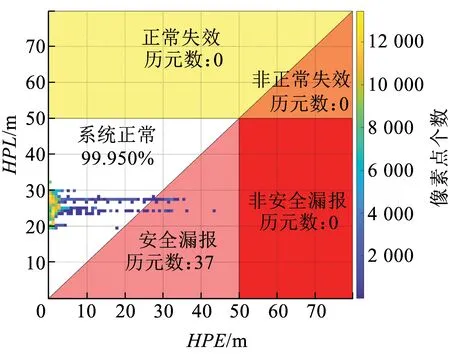
4 結論

