應用單層超表面實現聲波寬角度非對稱傳輸

李冰，徐輝宇，何靈娟，于天寶，劉文興，王同標，劉念華，廖清華

應用單層超表面實現聲波寬角度非對稱傳輸

李冰1，徐輝宇1，何靈娟1，于天寶1，劉文興1，王同標1，劉念華2，廖清華1

(1. 南昌大學物理系，江西南昌 330031；2. 南昌大學高等研究院，江西南昌 330031)

利用單層梯度超表面結構，設計并模擬驗證了一種實現聲波非對稱傳輸的方法，在較寬的角度范圍內實現了高對比度的聲波非對稱傳輸。經過恰當的超表面結構設計后，負折射現象實現了聲波的正向導通；高階衍射的抑制導致了反向入射的聲波傳輸被禁止。基于廣義斯涅耳定律分析了非對稱傳輸的原理，采用有限元法的數值模擬結果很好地驗證了理論分析。研究結果在噪聲控制、超聲整流或治療等方面具有潛在的應用價值。

聲學超表面；梯度超表面；非對稱傳輸；有限元法

0 引言

聲學超表面是由亞波長尺寸的結構單元在一個平面上排列而成的準二維結構[1-2]。超表面中每個單元對入射波的聲學響應(包括幅值、相位)可以獨立控制，通過調節超表面單元的聲學響應，可形成幅值、相位的重新分布，進而實現對入射波的幾乎任意的操控。利用超表面可以實現聲波的許多功能，如波束偏轉[3-5]，聲波的聚焦[6-7]和完美吸收[8]等。

作為一類十分重要的聲學現象，非對稱或單向傳輸已經得到了大量的研究。在實現聲學非對稱傳輸的傳統方法中，一方面，可利用非線性機制，打破時間反演對稱[9-10]，但這種方法存在非線性轉化效率低、實驗實現復雜等缺點；另一方面，也可采用非對稱幾何結構，破壞空間反演對稱[11-12]，但該方法存在著器件制作復雜、體積較大等問題，這都妨礙了聲學非對稱性傳輸的進一步的實際應用。近些年來，聲學超表面的出現為實現聲學非對稱傳輸提供了一條有效的新途徑。常見的報道是采用混合超表面結構實現聲波的非對稱傳輸[13-15]。混合超表面結構可由聲學超表面和聲子晶體組合構成[13]，也可由兩個或兩個以上的聲學超表面構成[14-15]。混合超表面結構的子單元通常采用了不同的設計方法。如梯度超表面和聲子晶體的組合[13]，在同一頻率下，利用超表面能夠改變聲波傳播方向和聲子晶體特定方向存在通帶或禁帶的特點，從而實現聲波的非對稱傳輸。對于多個超表面結構的組合[14-15]，通過設計不同的超表面幾何結構，造成不同超表面的有效折射率不同，當聲波從有效折射率較大的超表面一端入射時，在兩個超表面的界面出現全反射的現象，進而實現了聲波的非對稱傳輸。顯然，這類混合超表面的組合單元有著兩層或兩層以上的不同結構，因此仍然存在著設計和制備復雜、器件難以實現集成等問題。

最近，LI等[16]僅僅采用單層梯度超表面就實現了聲波的非對稱傳輸，其物理機制是通過引入固定損耗抑制了反向傳輸時的高階衍射，導致了聲波的反向傳輸消失。在沒有引入損耗的情況下，LIU等[17]把單層超表面平均分割成兩個超表面，通過超表面之間聲波的相干效應實現了聲波的非對稱傳輸。本文采用類似的單層梯度超表面，既無需引入損耗，亦無需分割超表面，通過合理的設計，在聲波反向傳輸時，高階衍射被抑制，實現了聲波寬角度、高對比度的非對稱傳輸。

1 理想模型和原理

首先，我們采用一個理想超表面模型說明聲波的非對稱傳輸機制。聲學超表面結構為單層，由周期性的超胞構建而成。圖1(a)分別給出了聲波沿正方向(Positive Direction, PD)、反方向(Negative Direction, ND)入射到聲超表面時聲波的傳輸途徑。入射角為，當聲波沿正方向斜入射時，聲波實現了負折射，從而實現了正向導通；當聲波沿負方向斜入射時，傳輸聲波轉換成了表面波，負方向無法導通，因此形成了典型的聲學非對稱傳輸現象。

圖1 基于單層聲學超表面的非對稱性傳輸示意圖和超胞結構示意圖

圖2 理想超表面結構中聲波實現單向傳輸的聲壓分布圖

下面分析這種非對稱傳輸的現象，入射聲波滿足廣義斯涅爾折射定律[21]：

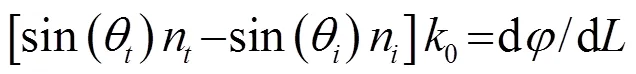
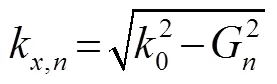
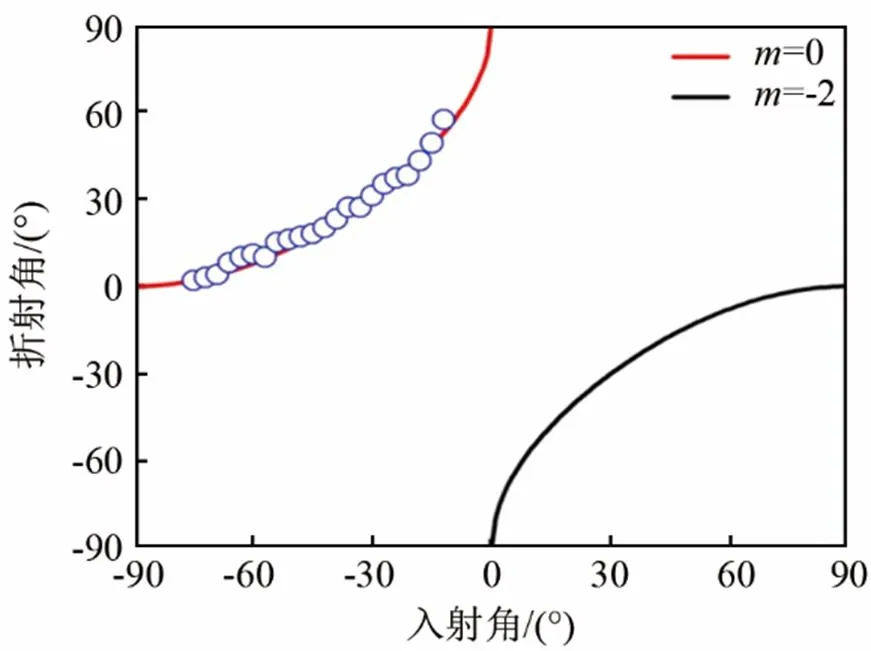
圖3 M=17時，折射角與入射角之間的關系

2 實際超表面的設計及模擬分析

圖4 實際超表面的結構示意圖以及各子單元的相位和透射率

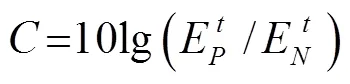
上述的模擬結果僅考慮了單個入射角，為了討論該非對稱傳輸器件的入射角容差，圖6(a)給出了在同一頻率3 430 Hz時，該超表面結構中透射聲能量對比度與入射角的對應關系。很明顯地可以看出，入射角從20o～65o的寬角度變化時，正反方向入射的對比度>15 dB，且在入射角為24o時達到了峰值17.41 dB，因此本文設計的非對稱傳輸對入射角度非常不敏感，實現了很大的入射角度容差。在損耗型單層超表面實現的非對稱傳輸中[16]，對比度的峰值僅約為10 dB，實現了15o～45o之間的>6 dB的能量對比度；與雙層耦合型超表面形成的非對稱傳輸性能相比[17]，本文的對比度的峰值提高了約3.81 dB，在20o～65o之間對比度普遍提升了近3 dB。因此，本文設計的非對稱傳輸器件與之前報道的結果相比，雖然結構相似，但非對稱傳輸的性能得到了顯著的提升。隨后，固定入射角為24o，計算得到了工作頻率從3 300～3 500 Hz的非對稱傳輸性能，透射能量對比度與頻率之間的變化關系如圖6(b)所示。在中心工作頻率(3 430 Hz)處達到最大值17.41 dB。一般對比度>6 dB時可以認為該結構具有了較好的非對稱傳輸性能[16]，從圖中可以看出，對比度>6 dB的頻率范圍分布于3 360～3 450 Hz之間，結果表明，在中心工作頻率附近較寬的頻率區間具有很好的非對稱傳輸性能。

圖5 實際設計的超表面結構中聲波實現單向傳輸的聲壓分布圖

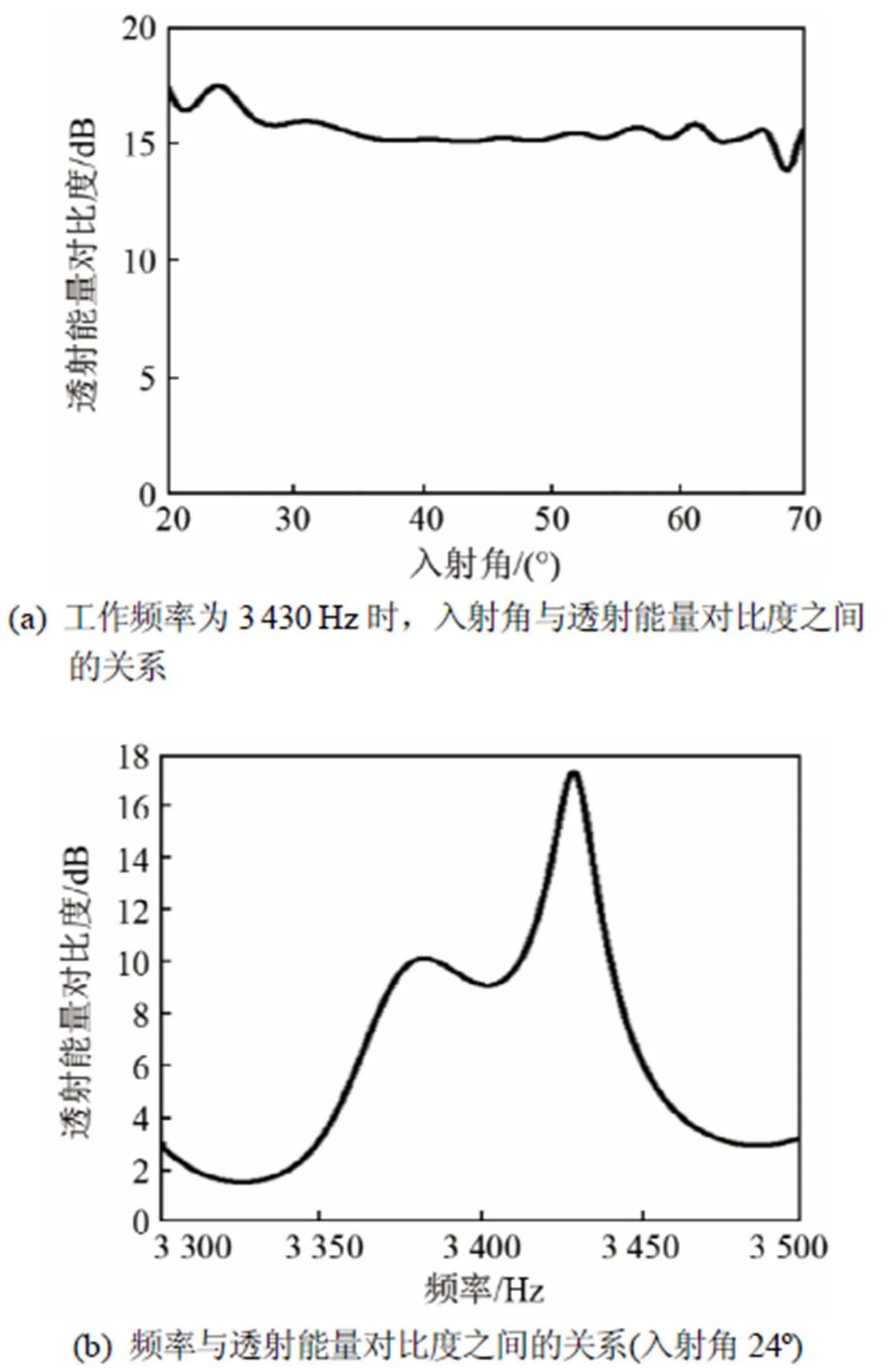
圖6 透射能量對比度與入射角、頻率之間的關系

3 結論

本文設計、分析及模擬了一種基于單層聲學梯度超表面的寬角度、高能量對比度的非對稱傳輸結構。正向斜入射時，負折射實現了聲波的正向導通；反向斜入射時，使超胞相位梯度和自由波矢相等，實現了高階衍射的抑制，從而禁止了聲波的反向傳輸。理論分析和數值模擬結果表明，透射能量對比度的峰值可達17.41 dB，在20o～65o的寬角度范圍內，對比度>15 dB。與之前報道的結果相比，本文的研究結果展現了更優的非對稱傳輸性能。

[1] 丁昌林, 董儀寶, 趙曉鵬. 聲學超材料與超表面研究進展[J]. 物理學報, 2018, 67(19): 10-23.

DING Changlin, DONG Yibao, ZHAO Xiaopeng. Research advances in acoustic metamaterials and metasurface[J]. Acta Phys. Sin., 2018, 67(19): 10-23.

[2] ASSOUAR B, LIANG B, WU Y, et al. Acoustic metasurfaces[J]. Nat. Rev. Mat., 2018, 3(12): 460-472.

[3] LI Y, QI S B, ASSOUAR B M. Theory of metascreen-based acoustic passive phased array[J]. New J. Phys., 2016, 18: 043024-1-19.

[4] HAN L X, YAO Y W, ZHANG X, et al. Acoustic metasurface for refracted wave manipulation[J]. Phys. Lett. A, 2018, 382(5): 357-361.

[5] LI Y, LIANG B, GU Z M, et al. Reflected wavefront manipulation based on ultrathin planar acoustic metasurfaces[J]. Sci. Rep., 2013, 3:2546-1-6.

[6] QI S B, ASSOUAR B M. Ultrathin acoustic metasurfaces for reflective wave focusing[J]. J. Appl. Phys., 2018, 123(23): 234501-1-8.

[7] QI S B, LI Y, ASSOUAR B M. Acoustic focusing and energy confinement based on multilateral metasurfaces[J]. Phys. Rev. Applied, 2017, 7(5): 054006-1-16.

[8] LI Y, ASSOUAR B M. Acoustic metasurface-based perfect absorber with deep subwavelength thickness[J]. Appl. Phys. Lett., 2016, 108(6): 063502-1-4.

[9] 林洲, 郭霞生, 程建春, 等. 聲二極管中聲傳播模型研究[J]. 聲學技術, 2013, 32(5): 353-356.

LIN Zhou, GUO Xiasheng, CHENG Jianchun, et al. Research on sound propagation model in acoustic diode[J]. Technical Acoustics, 2013, 32(5): 353-356.

[10] KAN W W, LIANG B, ZHU X F, et al. Acoustic one-way frequency up-converter with high transmission efficiency[J]. J. Appl. Phys., 2013, 114(13): 134508-1-6.

[11] 程營, 吳大建, 劉曉峻. 表面聲學超構材料中的非對稱聲傳輸研究[J]. 聲學技術, 2013, 32(5): 33-34.

CHENG Ying, WU Dajian, LIU Xiaojun. Asymmetrical transmission of sound wave in acoustic surface metamaterials[J]. Technical Acoustics, 2013, 32(6): 33-34.

[12] HE Z J, PENG S S, YE Y T, et al. Asymmetric acoustic gratings[J]. Appl. Phys. Lett., 2011, 98(8): 083505-1-3.

[13] SONG A L, CHEN T N, WANG X P, et al. Waveform-preserved unidirectional acoustic transmission based on impedancematched acoustic metasurface and phononic crystal[J]. J. Appl. Phys., 2016, 120(8): 085106-1-7.

[14] CHEN D C, ZHU X F, WEI Q, et al. Asymmetric phase modulation of acoustic waves through unidirectional metasurfaces[J]. Appl. Phys. A, 2018, 124(1): 1-6.

[15] SHEN C, XIE Y B, LI J F, et al. Asymmetric acoustic transmission through near-zero-index and gradient-index metasurfaces[J]. Appl. Phys. Lett., 2016, 108(22): 223502-1-4.

[16] LI Y, SHEN C, XIE Y B, et al. Tunable asymmetric transmission via lossy acoustic metasurfaces[J]. Phys. Rev. Lett., 2017, 119(3): 035501-1-5.

[17] LIU B Y, JIANG Y Y. Controllable asymmetric transmission via gap-tunable acoustic metasurface[J]. Appl. Phys. Lett., 2018, 112(17): 173503-1-5.

[18] 周光平, 楊奇, 李自光, 等. 超聲換能器激勵的板聲源振動特性的有限元分析[J]. 聲學技術, 2007, 26(2): 326-329.

ZHOU Guangping, YANG Qi, LI Ziguang, et al. Finite element analysis of transducer-driven vibration of plate[J]. Technical Acoustics, 2007, 26(2): 326-329.

[19] WANG Z, YU T B, WANG T B, et al. Acousto-optic interactions for terahertz wave using phoxonic quasicrystals[J]. J. Phys. D: Appl. Phys., 2018, 51(10): 1-10.

[20] YU T B, WANG Z, LIU W X, et al. Simultaneous large band gaps and localization of electromagnetic and elastic waves in defect-free[J]. Opt. Express, 2016, 24(8): 7951-7959.

[21] YU N F, GENEVET P, KATS M, et al. Light propagation with phase discontinuities: Generalized laws of reflection and refraction[J]. Science, 2011, 334(6045): 333-337.

[22] QIAN E T, FU Y Y, XU Y D, et al. Total omnidirectional reflection by sub-wavelength gradient metallic gratings[J]. Europhys. Lett., 2016, 114(3): 34003-1-5.

[23] MEI J, WU Y. Controllable transmission and total reflection through an impedance-matched acoustic metasurface[J]. New J. Phys., 2014, 16: 123007-1-11.

Wide-angle asymmetric sound wavetransmission in the single-layer metasurface

LI Bing1,XU Hui-yu1,HE Ling-juan1,YU Tian-bao1,LIU Wen-xing1,WANG Tong-biao1,LIU Nian-hua2,LIAO Qing-hua1

(1. Department of physics, Nanchang University, Nanchang 330031, Jiangxi, China; 2.Institute for Advanced Study, Nanchang University, Nanchang 330031, Jiangxi, China)

Based on the single-layer acoustic gradient-index metasurface, a method of realizing acoustic asymmetric transmission is designed and simulated. The asymmetric transmission exhibits the characteristics of wide-angle and high energy contrast. Via proper design of metasurface structure, positive propagation is permitted by negative refraction and negative propagation is prohibited by suppressing high order diffraction. The results of theoretical analysis using the generalized Snell’s law agree well with those of simulation based on finite element method. The design has potential application values in noise control, ultrasonic rectification and treatment.

acoustic metasurface; gradient metasurface; asymmetric transmission; finite element method

O424

A

1000-3630(2019)-03-0253-05

10.16300/j.cnki.1000-3630.2019.03.003

2018-12-26;

2019-03-14

國家自然科學基金(11664024、11704175)、江西省杰出青年基金(20171BCB23009)和江西省自然科學基金重點項目(20171ACB21020)資助。

李冰(1990－), 男, 河北邢臺人, 碩士, 研究方向為聲學超表面。

何靈娟,E-mail: helingjuan_123@163.com