航空發動機雙轉子系統不對中研究進展

張宏獻，李學軍＊，蔣玲莉楊大煉陳雨蒙

1.湖南科技大學 機械設備健康維護湖南省重點實驗室，湘潭 411201 2.廣西科技大學鹿山學院，柳州 545006

旋轉機械的轉子不對中是除轉子不平衡之外的一類最常見故障。不對中故障常引發轉子整體振動加劇、聯軸器偏轉、軸承及聯軸器磨損、轉子撓曲變形、轉定子碰磨、支撐負荷惡化、汽封間隙不均勻等故障。統計顯示［1－2］：旋轉機械不對中故障占轉子系統故障的60%以上；航空發動機整機振動與不對中相關的故障占到系統故障的50%～60%；40%的固定翼飛機和70%的旋轉機翼飛機存在的花鍵連接損傷問題都與不對中有關。

目前轉子系統不對中的研究主要集中在汽輪機、電機等串聯轉子系統的聯軸器不對中、滑動軸承不 對 中 等 方 面，夏 松 波［3］、劉 占 生［4］、韓 清凱［2，5］、Pachpor［6］等國內外學者對不對中的研究成果分別進行了綜述分析。航空發動機轉子系統由于轉速高、內外雙轉子通過中介軸承耦合、工作溫差大、支承結構復雜等原因，不對中故障問題嚴重。然而航空發動機雙轉子不對中的研究并未系統開展，本文分類綜述了與航空發動機雙轉子相關的不對中研究成果，為航空發動機雙轉子系統不對中故障研究提供參考。

1 航空發動機雙轉子系統相關的不對中研究現狀

不對中分為支承不對中和轉子不對中2大類。支承不對中是指一個轉子的軸心線與支承中心線不重合，其主要影響因素是支承結構（軸承和軸承座部件）的結構特征和力學特性，主要反映為軸承不對中故障。轉子不對中是指2個相鄰的、設計要求本應同軸的轉子，實際運行中它們的軸心線出現不同軸，其主要影響因素是連接聯軸器的結構特性和力學特性，反映為聯軸器不對中故障。航空發動機普遍采用滾動軸承彈性支承和剛性聯軸器連接，針對航空發動機轉子系統的這一結構特點，分別對以下3種不對中的研究成果進行分析。

1.1 滾動軸承不對中

一般將軸承不對中分為軸承偏角不對中和軸承標高不對中。也可以按照軸承類型分為滑動軸承不對中和滾動軸承不對中。航空發動機普遍采用滾動軸承支承，本文重點討論滾動軸承不對中。Harris和Kotzalas［7］又將滾動軸承不對中分為支承不同軸、軸承外圈傾斜、軸承內圈傾斜、軸變形4類，如圖1所示。

早在1971年，滾動軸承制造巨頭SKF公司的高級研究員Liu［8］采用數值分析的方法研究了直升機渦軸發動機高速圓柱滾子軸承內圈傾斜對軸承壽命的影響，如圖2所示：微小的角度傾斜量（1／3（°））對滾 子 接 觸 載 荷 分 布 的 影 響 已 經 很明顯。

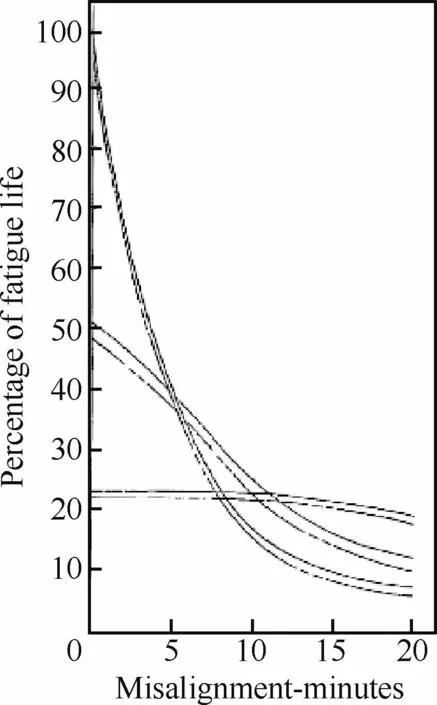
圖2 軸承壽命與不對中量的關系［8］Fig.2 Relationship of percentage of fatigue life of bearing vs misalignment［8］

隨后，更多的學者開始關注滾動軸承不對中的問題。白曉波等［9］研究也表明滾針修形量的大小與傾角存在很大的關系，適當的修形可以緩解滾針軸承內外圈傾斜所帶來的應力增加現象。Sharma［10］和 Cao［11］等研究滾動軸承內外圈不對中軸承疲勞壽命、載荷分布的影響也得到一致的結果。Aramakih［12］開發了一款滾動軸承剛度仿真軟件，程序中假設外圈固定，內圈五自由度，可用于仿真滾動軸承內圈不對中時軸承的載荷分布情況。Ye等［13］采用有限元法和擬動力學法研究了圓柱滾子軸承內外圈不對中載荷分布和接觸應力變化規律，發現隨著偏角不對中量的增加，軸承最大接觸力開始減小，后面逐漸增加到一個穩定的狀態。Bogdan和 Agnieszka［14］也發現軸承內外圈不對中會導致軸承疲勞壽命降低，且當徑向載荷較輕時，不對中對疲勞壽命的影響反而更大。李偉偉等［15］根據彈性接觸理論進一步研究發現，內外圈不對中導致滾子與內圈接觸時接觸應力在接觸副中間部分增大、兩端減小。滾子與外圈接觸時，接觸應力在接觸副兩端增大、中部減小。Mevel［16］提出一種新的非赫茲接觸算法計算滾動軸承內外圈傾斜時滾子接觸壓力的分布情況，通過與已有研究成果對比發現：雖然傳統線性赫茲接觸算法計算時間短，但新算法精度更高，更適合用于對滾動軸承內外圈傾斜時壓力分布的計算。Tong和Hong［17］也提出一種新的計算圓錐滾子軸承摩擦力矩的公式，并利用該公式分析滾動軸承內外圈偏角不對中對圓錐滾子軸承摩擦力矩的影響。研究發現施加不同的預緊載荷時，不對中的影響也不同。當施加恒定力載荷時，摩擦力矩隨不對中量增大而減小。施加較小預緊變形量時，摩擦力矩隨不對中量增加而增加，但施加較大預緊變形量時摩擦力矩隨不對中量的增大而減少。Park［18］采用有限差分法研究不對中量對滾動體彈性流體動力潤滑狀態的影響，發現微小的不對中量都將改變滾動體彈性流體動力潤滑的壓力分布和油膜厚度，最小油膜厚度隨著不對中量增加而快速降低。

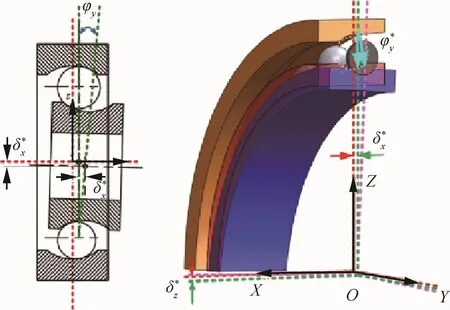
圖3 組合不對中狀態下的球軸承示意圖［20］Fig.3 Sketch of ball bearing with combined misalignments［20］

Ertas和Vance［19］通過實驗測試研究了角接觸球軸承內圈靜態不對中和外圈動態不對中對滾動軸承徑向剛度的影響。實驗發現靜態不對中時，軸承徑向剛度隨預加載和不對中量的增大而增大，外圈的動態不對中則降低了軸承徑向剛度。王美令［20］基于Hertz接觸理論建立了如圖3所示組合不對中狀態下的角接觸球軸承五自由度模型，研究發現轉子系統的固有頻率隨著軸承的平行不對中量的增大而逐漸增大，系統的固有頻率隨著組合不對中量的增大而增大，但增勢不明顯，并最終趨于恒定。在僅有平行不對中時，振動頻譜中只呈現單一的1倍頻，且其幅值隨著平行不對中量的增加而呈減小趨勢。

1.2 聯軸器不對中

聯軸器不對中的研究國內外都已經比較深入，聯軸器不對中動力學模型常采用3種方法獲得［4］：① 根據聯軸器結構特點，基于聯軸器的變形幾何關系和受力分析建模；② 采用有限元或集總參數法，將聯軸器看作轉子系統的一部分，用等效軸段建模；③ 對于自由度較少的轉子系統，采用系統整體Lagrange能量法建模。研究聯軸器不對中對轉子系統的影響的核心是推導不對中聯軸器的附加力（力矩）公式，并將附加力（力矩）代入轉子系統運動方程，最后進行動力學特性分析。常用的聯軸器不對中力學模型有Gibbons-Sekhar公式、Xu公式。

1976年，Gibbons［21］在前人研究基礎上，建立如圖4（a）所示的聯軸器不對中的坐標系，推導了平行不對中套齒聯軸器和彈性聯軸器附加力和力矩的計算公式。Askarian和Hashemi［22］利用Gibbons公式［21］計算不對中力，仿真結果顯示當系統存在不對中時發生2倍頻振動，且2倍頻大于1倍頻。在 Gibbons公式［21］的基礎上，Sekhar和 Prabhu［23］推導了偏角不對中力計算公式，如圖4（b）所示。Jalan和 Mohanty［24］等 利 用 Gibbons 公 式［21］和Sekhar公式［23］進行了理論分析和實驗驗證，數值仿真得到不對中系統的2倍頻振動信號，并通過實驗驗證了仿真結果。Prabhakar等［25］也根據Gibbons公式［21］和Sekhar公式［23］模擬轉子聯軸器不對中故障，并采用小波變化對不對中故障進行故障識別。

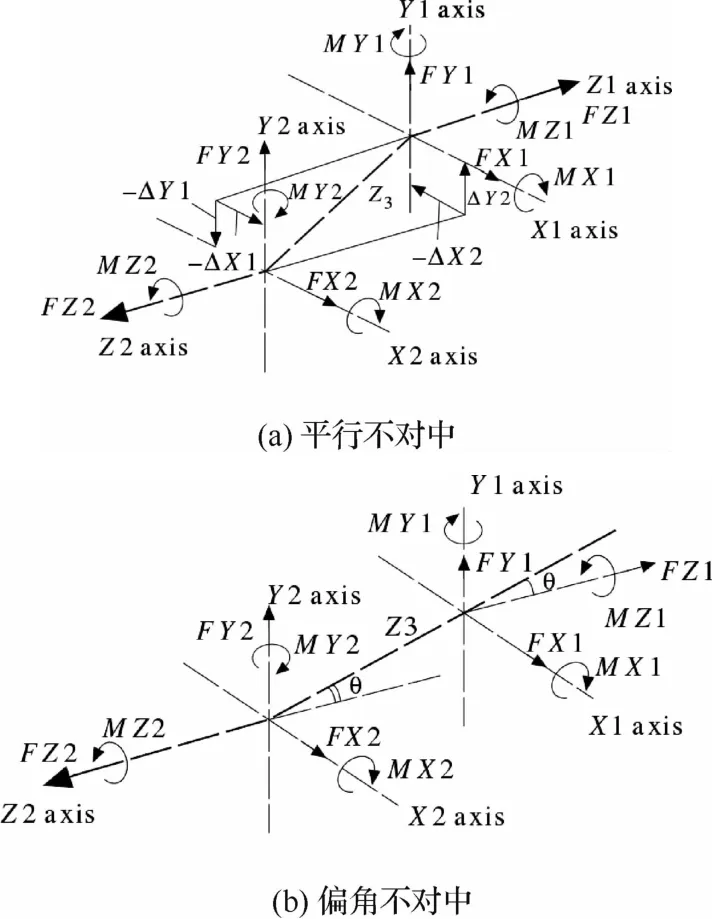
圖4 聯軸器不對中坐標系［21］Fig.4 Coupling coordinate system of misalignment［21］

1994年，Xu 和 Marangoni［26－27］推 導 建 立 了萬向節聯軸器存在偏角不對中時（如圖5所示）轉子之間附加力矩計算公式為

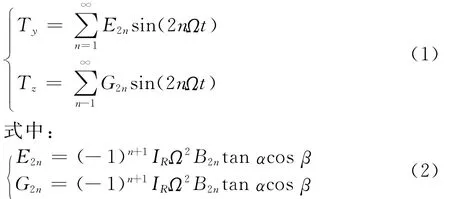
其中：T為驅動力矩；Ty，Tz分別為y軸和z軸的轉矩；α為驅動轉子（Motor）與被驅動轉子（Rotor）間的不對中角度；β為驅動轉子空間方位角；Ω為轉子轉速；B2n為角加速度的傅里葉級數展開系數；t為時間；IR為轉子的轉動慣量。

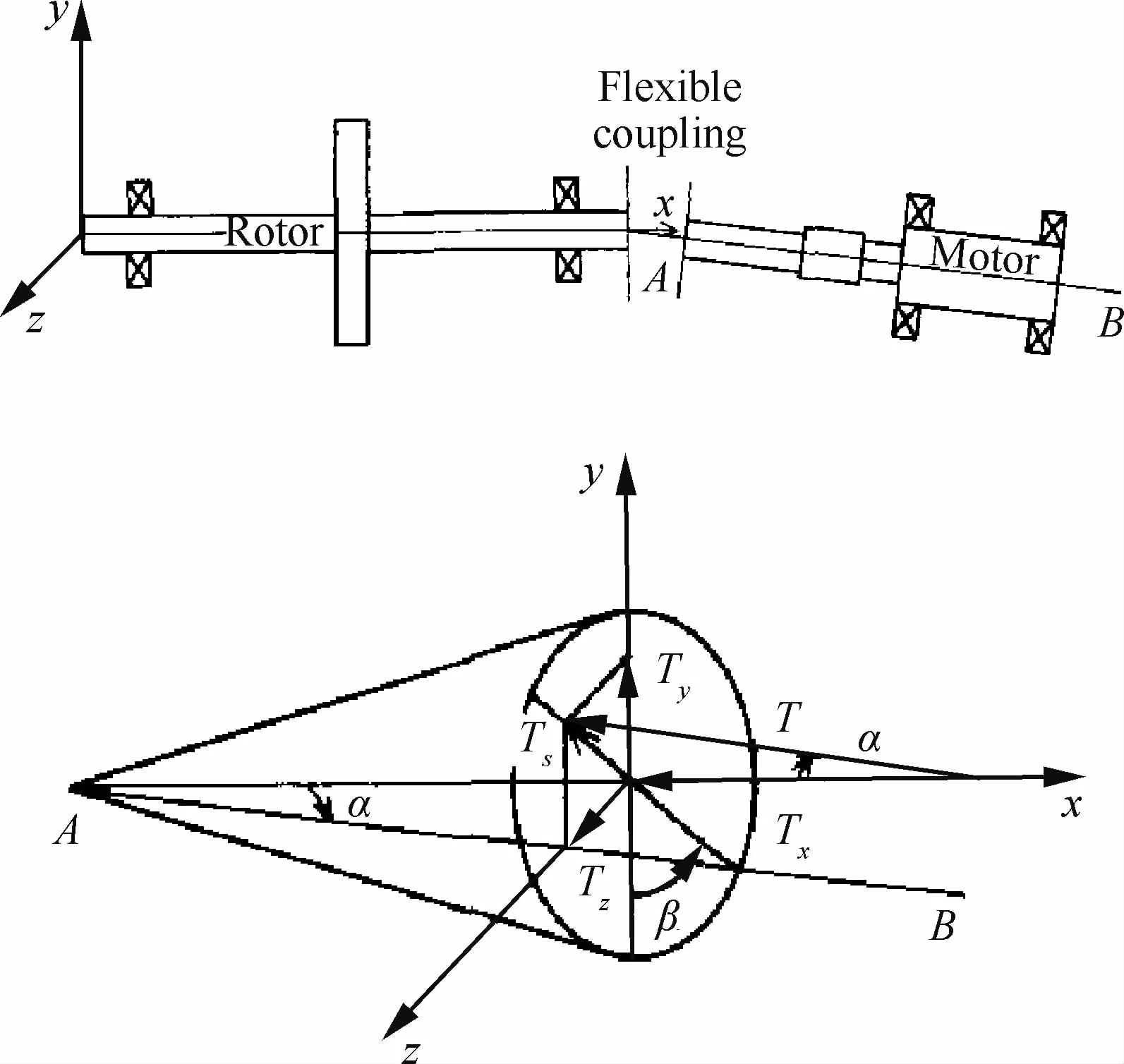
圖5 轉子不對中狀態的轉矩分解圖［26］Fig.5 Schematic of rotor misaligned system and its torque components［26］

Xu公式相對Gibbons公式和Sekhar公式更加簡潔，通用性更強得到了更廣的應用。劉楊等［28］利用 Xu公式［26］推導不對中力，研究了滑動軸承支撐下轉子系統不對中、碰摩耦合故障特性，并用實驗驗證了理論分析結果。Hili［29］和Fakhfakh［30］等假設轉子剛性、軸承線性支承，也采用Xu公式研究了轉子聯軸器存在偏角不對中的振動特性，發現偏角不對中引起轉子系統2倍頻振動，平行不對中則不能激起2倍頻振動。李明和李自剛［31］借鑒Xu公式的分析方法進行不對中力學分析，并通過搭建轉子系統實驗臺，實驗驗證了不對中產生的頻譜特性。國內的韓捷［32－33］、李明［31，34］、趙廣［35－37］等學者對 齒 式 聯 軸 器、花鍵 聯軸器不對中力學模型的研究也進行了深入的研究，取得了豐碩成果。王永亮等［38］針對航空花鍵的失效、潤滑、振動、磨損、不對中、轉子動力學、實驗研究等方面進行了詳細的調研分析和歸納總結，特別指出不對中是引起花鍵及其轉子系統振動及失穩的根源之一，并總結歸納了花鍵不對中的控制準則。

1.3 航空發動機雙轉子不對中

隨著我國航空事業發展，航空發動機轉子動力不對中問題也受到越來越多關注［39］。針對航空發動機雙轉子不對中的結構特點，韓清凱等［2］將航空發動機雙轉子系統不對中分為風扇段轉子支點不對中、高壓段轉子支點不對中、低壓段轉子聯軸器不對中、低壓轉子支點不對中、高壓段轉子不同心、內外雙轉子不對中6種形式，并具體分析了6種不對中的特點。

蔣玲莉等［40］采用CATIA軟件建立某型航空發動機雙轉子系統三維模型，并利用Ansys軟件進行模態分析，發現平行不對中使系統的固有頻率降低。針對航空發動機偏角不對中問題。馮國全等［41］將外轉子支撐軸承不對中的激勵作用等效為外轉子軸承處的不對中彎矩，用該彎矩模擬外轉子支撐軸承的不對中，建立了考慮軸承不對中時的雙轉子系統有限元模型（圖6），仿真結果表明，內外轉子的振動均出現2倍頻成分，且隨著不對中程度的加大，2倍頻成分也明顯增大且會占主導，軸心軌跡會從近似圓形變化為8字形。

李洪亮［42］充分考慮了航空發動機雙轉子系統的支撐軸承和中介軸承的軸承間隙、滾珠與滾道的非線性赫茲接觸以及軸承變剛度特性，研究內外轉子存在偏角不對中時的動力學特性，數值分析表明內外轉子偏角不對中導致系統2倍和工頻成分突出，轉子軸心軌跡呈現“香蕉”形，且不對中角度越大，2倍頻成分越突出，容易引發劇烈的二倍超諧波共振。李全坤等［43］建立了內轉子聯軸器綜合不對中時的雙轉子不對中故障系統動力學模型。數值分析和實驗驗證結果表明：由于高壓轉子采用中介軸承的支承方式，低壓轉子的2倍頻不對中振動會傳遞至高壓轉子，在雙轉子系統臨界轉速的1／2處會發生2倍頻共振。

圖6 內外雙轉子系統有限元模型［41］Fig.6 Finite element model for dualrotor system［41］

陳果和李興陽［44－45］考慮滾動軸承變剛度支承和聯軸器不對中耦合作用，建立了轉子-滾動軸承系統動力學模型，省略了高壓壓氣機轉子，設高壓壓氣機轉子與高壓渦輪轉子間以套齒聯軸器聯結，建立了含不平衡-聯軸器綜合不對中-碰摩耦合故障的轉子滾動軸承機匣耦合動力學模型（圖7），研究發現：由于不對中引起的2倍頻將導致的轉子轉速在1／2臨界轉速時引起共振，2倍頻隨平行不對中量的增加線性增加，基頻則保持不變；當不對中和碰摩故障耦合作用時，在臨界角頻率以上時，將出現分頻和混沌現象，且隨著不對中量的增加，混沌現象減少，系統趨于穩定。

劉永泉［46］和 Ren［47］等分別針對航空發動機三支點柔性轉子系統的支承不同心問題建立了轉子系統的力學模型。數值分析結果顯示除了2倍頻外，還發現支承不同心不僅引起轉子過渡軸的剛度非線性變化還會給轉子系統帶來附加不平衡激勵，且轉子系統2倍頻分量隨不同心量的增加而迅速增加，而1倍頻分量基本保持不變（圖8），這與李興陽和陳果［48］的研究結果相吻合。Li等［49］也建立了三支點轉子平行不對中模型，通過分析時域和頻域信號發現1倍頻（1×harmonic）和2倍頻（2×harmonic）均隨平行不對中量先增大后減小（圖9），最終趨于穩定，這一結果與劉永泉等［46］的結果不一致。由此可見針對航空發動機不對中的研究仍需繼續深入，并采用模擬實驗進行驗證。

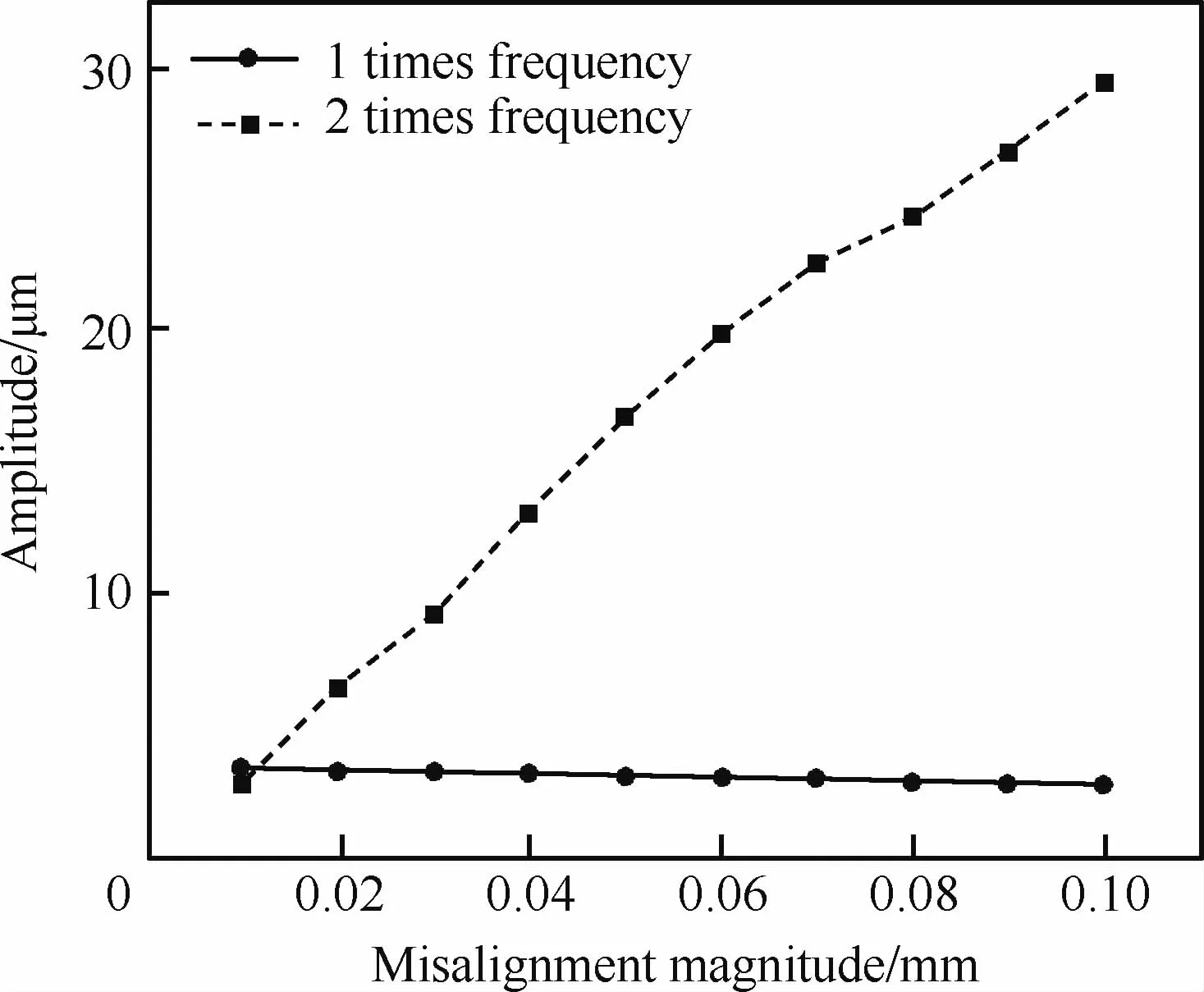
圖8 振幅在各倍頻隨不對中量變化情況［46］Fig.8 Variation of amplitude of each frequency component with misalignment magnitude［46］

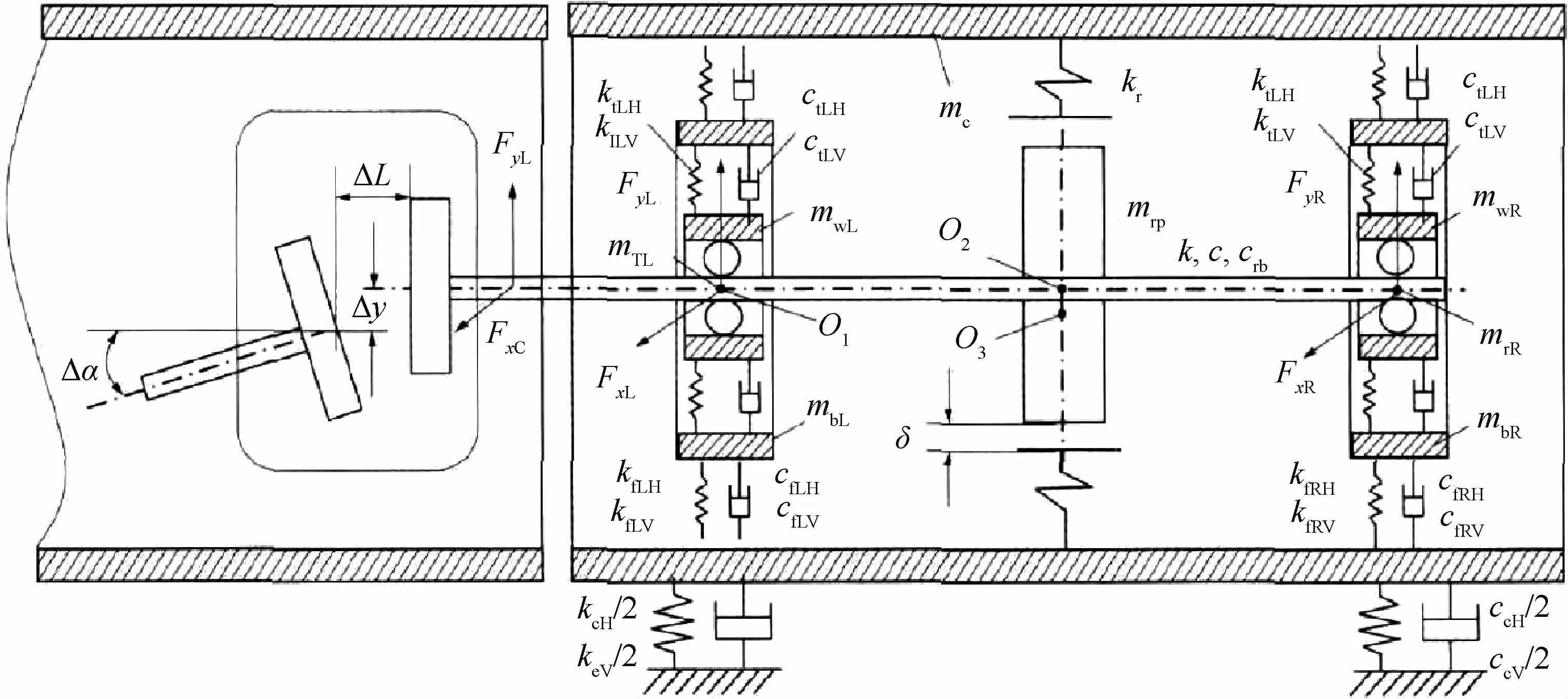
圖7 不平衡-不對中-碰摩耦合故障的轉子-滾動軸承-機匣耦合動力學模型［44］Fig.7 Rotor-ball bearing-stator coupling dynamic model for imbalance-misalignment-rubbing coupling faults［44］

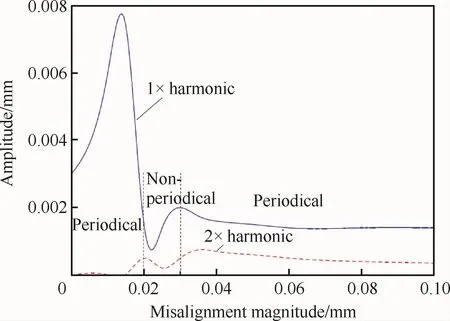
圖9 振動倍頻隨不對中量變化情況［49］Fig.9 Variation of frequency doubling misalignment magnitude［49］

2 不對中問題新研究熱點

隨著不對中的研究日益深入及旋轉機械的高速化、柔性化發展，不對中問題的研究熱點也發生新的變化。查閱近年文獻，國內外學者們更多地關注不對中的非線性動力學特性、不對中故障定量分析與診斷等新方向。這些不對中的最新研究成果，對于航空發動機雙轉子系統不對中故障診斷與分析的研究也有重要的借鑒意義。

2.1 不對中轉子系統非線性動力學研究

隨著混沌理論在轉子動力學的應用，不對中導致的非線性問題也日益引起關注。比如分岔、混沌運動及不對中對轉子系統穩定性的影響。

Li等［50］分析了不對中轉子系統的非線性動力學特性，結果顯示：不對中導致的橫向振動在低速穩態運行時與轉子系統的振動是同步的，隨著速度的提高則產生嚴重的分岔及混沌運動。Li Z G和Li M［51］假設滑動軸承為長軸承，研究了轉子存在平行不對中時的非線性動力學特性，通過系統的穩態響應、軸心軌跡、龐加萊映射和李雅普諾夫數分析，得到了與Li等［50］一致的結果。李洪亮等［52］針對滾動軸承支承轉子系統的非線性支承，采用諧波平衡法-時頻域轉換技術研究了聯軸器不對中轉子系統的非線性動力學響應。Ma等［53］綜合考慮球軸承的潤滑、彈簧剛度、擠壓油膜阻尼器間隙以及套齒聯軸器不對中的耦合作用，通過對比分岔圖和龐加萊映射圖得知，不對中將提高轉子系統的失穩轉速和分岔開始轉速，但不對中也縮短了系統的穩定性運行的范圍。Al-Hussain［54］采用李雅普諾夫方法研究不對中對柔性聯軸器-滑動軸承-剛性轉子系統穩定性的影響，如圖10所示，隨著不對中角度α的增加，穩定運行區域的逐漸擴大。Yi等［55］的研究也表明不對中對轉子的整體穩定性和不對中軸承的振動影響顯著。且當不對中量大于軸承間隙時，不對中導致轉子系統從不穩定區域進入周期運動，適當的不對中有利于軸承-轉子系統動力學特性。

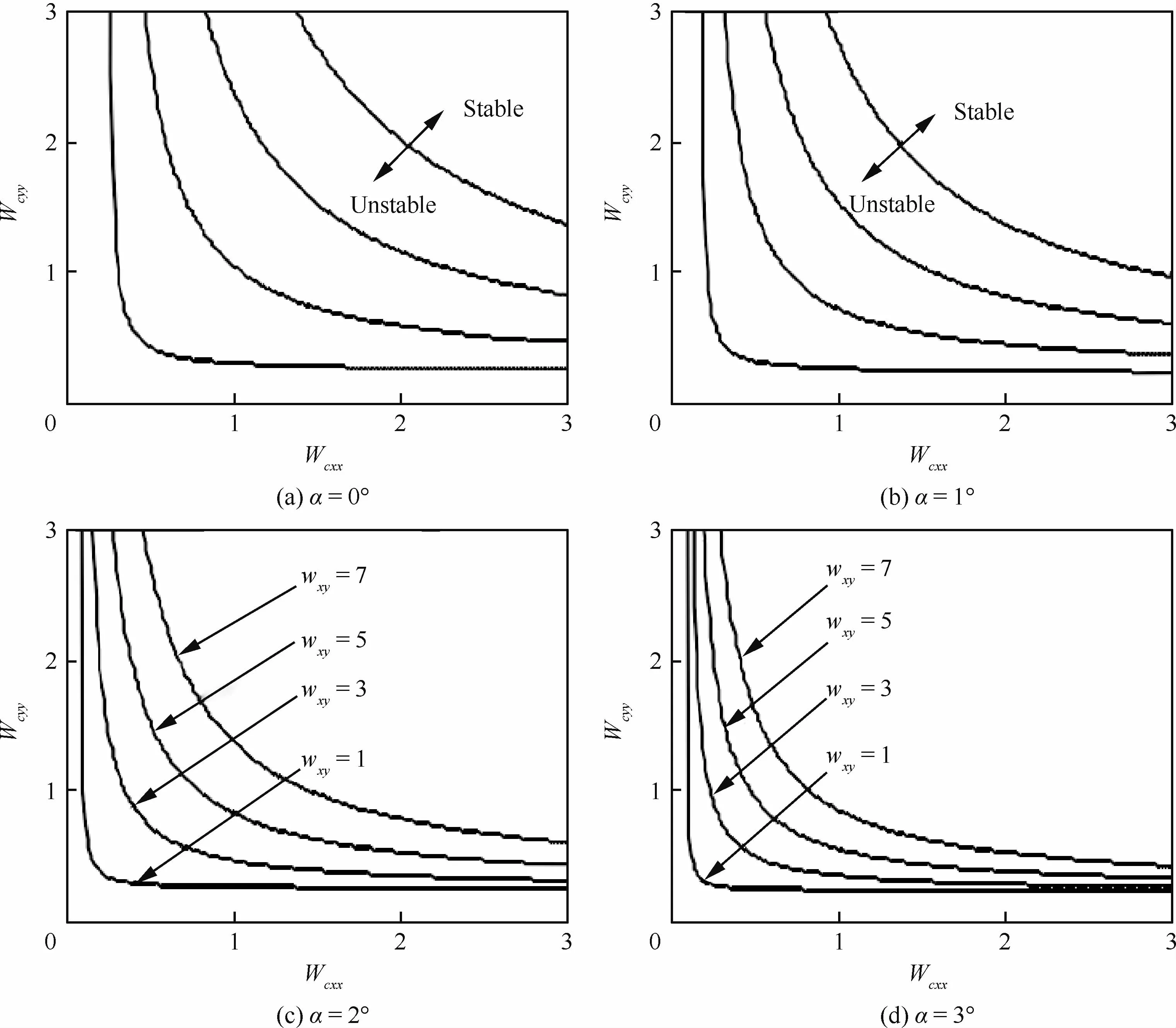
圖10 不對中角度對穩定性的影響［54］Fig.10 Effects of angular misalignment on stability［54］

Huang等［56］研究了水輪發電機轉子系統（立式轉子）存在平行不對中時轉子系統的動力學特性，發現平行不對中導致轉子系統發生周期、3倍周期、擬周期運動，同時導致系統存在低頻（0.3～0.4倍頻）振動。Luneno等［57］也研究水電站立式水輪機轉子的止推軸承存在不對中時的轉子系統的動力學特性，引入不對中參數的數學模型顯示：不對中會使立式轉子系統在一定的轉速范圍內存在不穩定，隨著不對中量的增大，不穩定區域也增加，且不穩定區域在臨界轉速以下也可能出現，這將對轉子系統穩定運行產生較大影響。Thiery和Aidanpaa［58］也通過數值仿真和實驗測試研究了水輪機立式轉子系統由于平行不對中導致的轉子、定子碰摩非線性振動特性。

申屠留芳等［59］研究了疊片聯軸器在偏角不對中故障下系統的非線性動力學行為，采用數值方法對微分方程進行仿真求解，繪制出了系統運動隨轉速變化和角不對中量變化的分岔圖。Zhang等［60］采用 MATLAB和Adams聯合仿真分析了考慮不平衡-不對中-碰摩耦合故障的柔性轉子-滾動軸承系統的幅頻特性，發現不對中故障將導致系統產生2倍頻和高階頻次的諧振。Ma等［61］針對不對中造成的轉子和定子碰摩故障導致的非線性動力學特性進行了分析。Nikolajsen［62］采用傳遞矩陣法、有限元法和影響因子法3種方法研究了不對中量對超靜定4支點滑動軸承支承結構轉子系統失穩臨界值的影響，發現失穩臨界值既不是在完全對中狀態也并非在4個軸承均勻承擔載荷的狀態，失穩臨界值隨不對中量的變化類似于“W”型。

綜上所述，不對中的產生導致系統存在非線性動力學行為。但上述不對中對非線性動力學特性的研究均假設不對中是確定性發生的，而工程實際中可能是動態、隨機發生不對中問題，并且不對中量的大小往往未知。針對隨機不對中問題，Li等［63］則利用蒙特卡羅法研究了不對中量隨機發生時轉子系統的非線性動力學特性，通過建立的不對中隨機模型，仿真發現了不對中轉子的超諧共振現象（即1／2臨界轉速處產生共振），研究還發現支承阻尼、支承剛度的概率分布密度對不對中轉子穩定工作范圍有較大影響，為不對中故障的研究提供了新的思路。

2.2 不對中故障定量分析

隨著不對中問題研究的深入，人們對不對中轉子系統的動力學特性已經有較深入的研究，但不對中故障的發生位置的定位檢測、定量分析、在線抑制研究仍然不足，也嚴重影響了不對中的故障分析與診斷效果。

馬波等［64］針對透平機聯軸器平行不對中故障程度難以定量診斷的問題，基于轉子的狀態監測數據建立轉子平行不對中量與節點振動幅值的關系，實現定量診斷轉子平行不對中故障的方法。陳宏等［65］針對傳統的基于單通道信號的旋轉機械不對中故障的診斷主要依靠幅值譜和相位譜特征易出現誤診和漏診情況，提出了基于全矢譜技術的不對中故障診斷方法，通過對互相垂直的2個通道信號的融合，不但能夠提高對不對中特征提取的可靠性，而且能夠給出不對中的具體方向。在此基礎上，陳宏等［66－67］又從運動學角度分析了雙跨轉子系統的運動特性和運動形態，提出了一種轉子動態不對中量的定量計算方法。Lees等［68］提出通過一次啟停機檢測不對中和不平衡的方法，利用不對中在聯軸器處產生的附加力矩和附加力定量測量不對中大小，對于柔性轉子剛性聯軸器滑動軸承支撐轉子可以利用在滑動軸承處產生的附加載荷定量測量不對中大小。雖然該方法可實現一次啟停機測量不對中量，但由于需要先測量軸承處的絕對振動而使該方法推廣使用受限。Lal和Tiwari［69］提出通過測量基頻振幅定量估算轉子系統平行和角度不對中量的方法，并搭建轉子實驗臺進行了驗證。Rybczyski［70］通過分析滑動軸承軸心軌跡與轉子旋轉方向的關系及軸心軌跡位置與軸心軌跡大小的關系對轉子系統的不對中故障進行診斷，并以一個由7個滑動軸承支承的汽輪機轉子進行說明，根據軸心軌跡蘊含的動力學信息判斷轉子不對中狀態。

除了上述通過測量振動信號對不對中進行故障診斷，也有學者嘗試利用不對中電機電流信號、旋轉力矩的變化進行不對中故障診斷。Verucchi等［71］利用異步電機轉子系統中電機的負荷轉矩和電機電流信號的變化來診斷不對中故障。通過對電流信號和轉矩信號進行頻譜分析，發現不對中導致電機負荷轉矩出現基頻、2倍頻、3倍頻明顯增大，同時使電流均值明顯減小，據此可以通過測量電機負荷轉矩和電流信號判斷電機與驅動轉子是否存在不對中故障。而Reddy和Sekhar［72］則提出通過測量轉子系統傳遞的旋轉力矩信號來判斷是否存在不對中故障，對采集的旋轉力矩信號進行快速傅里葉變換和小波變換，結果表明：不對中轉子系統的加速度振動信號和旋轉力矩信號均出現2倍頻，且兩者的基頻幅值和2倍頻幅值均隨不對中量的增加而增加，但旋轉力矩增加的速度沒有加速度增加的速度明顯；通過對比小波變換和快速傅里葉變換2種方法，發現小波變換對不對中量的變化更加敏感且曲線更加光滑，更適合于不對中的狀態識別。Qi等［73］也采用基于小波包分析和經驗模態分解提出一種新的信號處理方法，并成功應用于三支點轉子系統不對中振動信號的故障診斷。

相對于不對中故障分析和故障診斷，不對中故障處理一般在要在停機狀態完成。高金吉院士［74］提出人工自愈的概念，即在機器設備不停機的狀態下，通過機器自愈調控系統抑制機器可能產生的損壞力使其不產生或在運行中自行消除故障。余棟棟等［75］設計了一種整體式擠壓油膜阻尼器并將其應用于不對中振動的抑制，是不對中故障在線抑制的一次有益嘗試。而不對中故障在線主動控制的研究還是一片空白。

3 結論與展望

綜上所述，國內外關于轉子系統不對中的研究取得了豐碩的成果，對開展航空發動機雙轉子不對中研究有重要的借鑒意義。但針對航空發動機雙轉子系統不對中問題，以下幾個方面的問題還有待于進一步深入研究：

1）航空發動轉子系統彈性多支承不對中動力學特性研究。航空發動機采用滾動軸承彈性支承、支點多、跨度大、工作溫差大，不對中問題更加復雜。熱變形與彈性支承可能造成動態不對中問題，內外轉子中介軸承的耦合也有別于普通不對中轉子，航空發動機處于機動飛行狀態下不對中的影響也未見報道，這些問題都需要進一步深入開展。

2）航空發動機轉子系統不對中故障的非線性動力學分析。目前對滑動軸承不對中的非線性問題研究成果較多，航空發動機采用滾動軸承存在非線性變剛度支承，且內外轉子耦合，非線性激勵多，非線性特性明顯。雙轉子不對中的非線性動力學研究及穩定性研究也有待深入。

3）航空發動機雙轉子不對中的定量分析與在線抑制。不論普通旋轉機械，還是航空發動機雙轉子，不對中故障的定量分析與在線抑制問題都是一個難題，相關的研究成果不足。航空發動機工作條件惡劣，難以直接采集轉子振動信號，研究航空發動機振動信號傳遞衰減特性，提取有效不對中振動信號也是一個挑戰。定量分析與在線抑制對提高轉子不對中故障診斷準確率，保障設備的正常安全運行都意義重大，仍有許多工作需要深入開展。