Relativistic Self-Focusing of Hermite-cosine-Gaussian Laser Beam in Collisionless Plasma with Exponential Density Transition

Vishal Thakur,Manzoor Ahmad Wani,and Niti Kant,?

1Department of Physics,Lovely Professional University,Phagwara-144411,Punjab,India

2Govt.Higher Secondary School Waterhail,Budgam-191111,J&K,India

AbstractThis work reveals an exploration of self-focusing of Hermite-cosine-Gaussian laser beam in a collisionless plasma under relativistic nonlinearity.Self-focusing along with self-trapping of Hermite-cosine-Gaussian laser beam are analyzed for different values of laser intensity,plasma density,and decentered parameters.Mathematical analysis displays that these parameters play a major role in achieving the stronger and earlier self-focusing.Further,a comparative study between self-focusing of Hermite-cosine-Gaussian laser beam with and without exponential density ramp profile is introduced.Plasma density transition with exponential profile is found to be more effective in order to have stronger self-focusing.The present analysis may lead to very useful applications in the field of efficient harmonic generation,laser driven fusion etc.

Key words:self-focusing,collisionless plasma,exponential plasma density ramp,Hermite-cosine-Gaussian laser beam

1 Introduction

Self-focusing of the laser beam with high intensity propagating through preformed plasma channel has been a subject of abundant interest in last few years,as they play an important role in high power laser applications like,laser-driven plasma accelerators,[1?4]X-ray lasers,[5]inertial con finement fusion,[6]harmonic generation[7?8]etc.The phenomenon of self-focusing,[9?11]fi lamentation and self-trapping of the laser beam was stated by Akhmanov et al.[12]and then established by Sodha et al.[13]Behavior of quadruple Gaussian laser beam in inhomogeneous magnetized plasma under linear absorption and ponderomotive nonlinearity was studied[14]and it was concluded that diverging beam shows oscillatory divergence while converging beam shows oscillatory convergence.

influence of density transition on self-focusing of laser in plasma was studied[15]and it was concluded that an earlier and efficient self-focusing of the laser can be observed with density transition whereas due to linear absorption weaker self-focusing occurs in plasma.A remarkable inlf uence of the intensity and decentered parameters on selffocusing of Hermite-cosine-Gaussian laser beam with collisionless plasma was observed.[16]For the study of selffocusing of cosh Gaussian laser beam in quantum plasma,higher order paraxial theory was presented by Habibi and Ghamari.[17]They found that by selecting the optimized decentered parameter,effective self-focusing is witnessed for cosh Gaussian laser beam as compared to Gaussian beam.In addition to this,the role of quantum effect was seen in the embellishment of self-focusing of the laser during laser plasma interaction.[18?19]Self-focusing of the Hermite-cosh-Gaussian laser beam propagating in semiconductor quantum plasma was analyzed by Wani et al.[20]They observed the influence of the decentered parameter,laser intensity and density ramp on self-focusing of Hermite-cosh-Gaussian laser beam with strong and earlier effects in semiconductor quantum plasma.

Bokaei et al.[21]reported that below a fixed electron temperature ponderomotive force favors relativistic selffocusing for the given initial laser intensity whereas above this temperature self-focusing vanishes.Hence,it is signi fi cant to examine the combined effects of ponderomotive and relativistic self-focusing on the growth of the laser beam in plasma.In lieu of this a report was presented along with longitudinal phase shift with the decreased value of the beam width parameter for strong selffocusing.[22]

A model was developed to analyze non-stationary ponderomotive self-focusing of a Gaussian laser beam in the cold plasma and stronger self-focusing was reported at the rear of the pulse than at the front.[23]Ponderomotive self-focusing in collisionless isothermal plasma was examined by Wang and Zhou.[24]Further,this theory was revised by introducing the effect of upward plasma density transition.[25]By considering relativistic saturating nonlinearity self-focusing of the laser beam in axially inhomogeneous plasma was investigated by Asthana et al.[26]It was observed that beam width parameter achieves a constant value reliant upon the initial laser intensity and the plasma inhomogeneity.Further,self-focusing of the quadruple Gaussian laser beam in an inhomogeneous medium along with saturating nonlinearity in the paraxial approximation by including the influence of linear absorption and external magnetic field was studied by Aggarwal et al.[14]They found that the density depletion is created because of the ponderomotive force,which expels the electrons away from the axis where intensity is maximum.

The purpose of this work is to analyze self-focusing of Hermite-cosine-Gaussian laser beam in a collisionless plasma with relativistic nonlinearity.Self-focusing along with self-trapping of Hermite-cosine-Gaussian laser beam are noticed for different values of laser intensity,plasma density,and decentered parameters.It is observed that with the increase in the intensity of laser beam the process of self-focusing becomes efficient.Also with the increase of the plasma frequency self-focusing becomes more efficient and occurs earlier.

The paper is organized as follows:In Sec.2,we have solved equation of the beam width parameter f of the Hermite cosine Gaussian laser beam with the normalized distance of propagation ξ.Results and discussion are given in Sec.3.Finally conclusion is given in Sec.4.

2 Theoretical Considerations

Electric field distribution of Hermite-cosine-Gaussian laser beam passing through collisionless plasma along zaxis can be taken in the form of

where E0represents constant amplitude of electric field,Hmand Hnare the m-th and n-th order Hermite polynomial respectively,?0is the parameter related to cosine function,r0is the waist width,f1(z)and f2(z)are the beam width parameters in x and y directions respectively.

The dielectric constant is given as

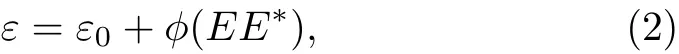
where ε0=1 ? ω2p/ω2,ω2p=4πn(ξ)e2/m,m=m0γ,? shows the dielectric constant for nonlinear part,ωpis plasma frequency and ω shows the angular frequency of laser beam.Plasma density ramp can be considered as n(ξ)=n0exp(ξ/d),where ξ=z/Rd,is normalized distance of propagation,Rd=kr20shows di ff raction length,n0is the equilibrium electron density,e and m0are charge on the electron and rest mass respectively.

The nonlinear dielectric constant for collisionless plasma can be given as[27]

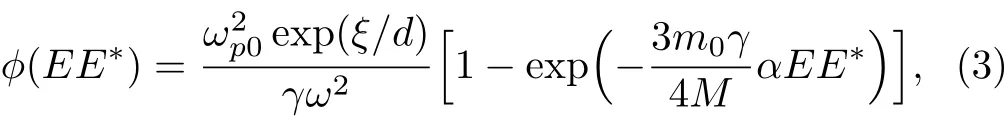
where α =e2M/6m20γ2ω2kBT,T is the plasma temperature,M is the mass of scaterrer,and kBis the Boltzmann constant.

The laser beam propagation can be expressed as

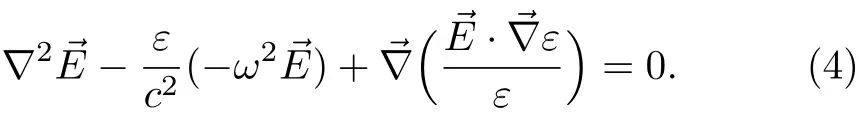
Following WKB approximation above equation becomes

Further,A can be expressed as

where,k=(ω/c)ε10/2and Amnand S depend on x,y,and z.Now differentiate Eq.(6)with respect to x,y,and z and substitute the values in Eq.(5),we get

Now,equating real and the imaginary parts on both sides of Eq.(7)we get real part is

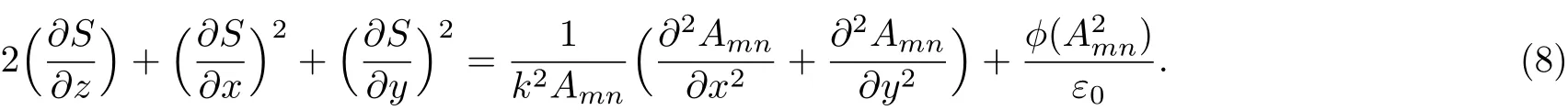
Imaginary part is

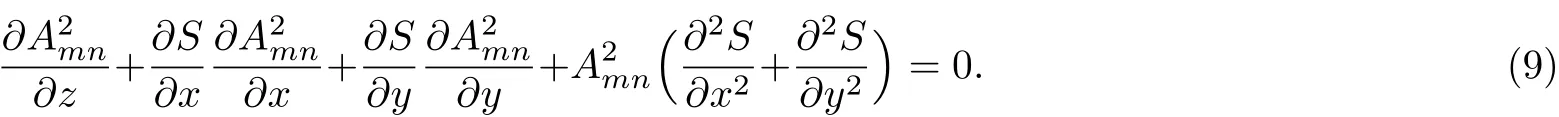
The solutions of Eqs.(8)and(9)can be given as:

where,β1(z)=(1/f1(z))(?f1/?z)and β2(z)=(1/f2(z))(?f2/?z)signify the curvature of the wavefront in the x and y directions respectively.Considering the mode for which,m=0 and n=0,we haveandFurther,employing the paraxial approximation and differentiating Eqs.(10)and(11)and equating coefficients of x2and y2on both sides and using ξ=z/Rd,where,Rd=kr20we get

Similarly

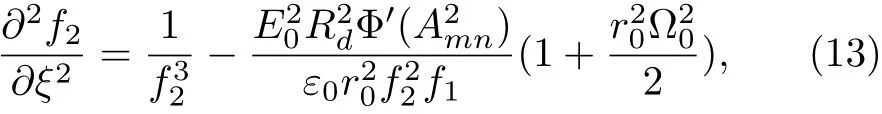
where

After simplifying the Eqs.(12)and(13)we obtain the expressions for the beam width parameters f1and f2as:

where b=r0?0is decentered parameter and ξ is the dimensionless propagation distance.Equations(14)and(15)are the essential expressions for beam width parameters f1and f2respectively.

2.1 Self-Trapped Condition

For originally plane wavefront,(?f1/?ξ)ξ=0= 0,(f1)ξ=0=1 and(?f2/?ξ)ξ=0=0,(f2)ξ=0=1,the conditions ?2f1/?ξ2=0 and ?2f2/?ξ2=0 cause the propagation of laser beam in self-trapped mode.Using these values in Eqs.(14)and(15)respectively,one can have relation for the dimensionless initial beam width ρ0(=r0ω/c)with αE20.

3 Results and Discussion

Equations(14)and(15)are numerically solved analogous to an original plane wave front,for ξ=0,f1=1,?f1/?ξ=0.Consider plasma exposed to a 1.06μm Nd:YAG laser(corresponding intensity I0≈5×1017W/cm2).In Fig.1 effect of self-focusing of Hermite-cosine-Gaussian laser in plasma with and without exponential plasma density ramp is seen.The other terms are ωp0/ω =0.6,αE20=1.25,m0/M=0.02,r0ω/c=50,γ =1.25,d=8,and b=2.One may clearly notice from Fig.1 that the process of self-focusing(f1=0.13)becomes efficient at ξ=5,with exponential plasma density transition as compared to without plasma density transition(f1=0.54).Hence,it may be concluded that efficient self-focusing is noticed by considering exponential plasma density transition.

Figure 2 shows the dependence f1and f2on ξ for various values of ωp0/ω =0.4,0.5,and 0.6.The other terms are same as taken in Fig.1.One may notice that with the rise in plasma frequency process of self-focusing is found to be more prominent and efficient self-focusing(f1=0.13)is obtained at ξ=5.Also,with an increase in plasma density,the number of electrons contributing to self-focusing increases.The present observation is in good agreement with 3D PIC simulation results reported by Pukhov and Meyer-ter-vehn.[28]

Fig.1 Comparison between the effects of exponential plasma density ramps and without density ramp on the dependence of f1and f2on ξ. The other parameters are ωp0/ω =0.6,αE20=1.25,m0/M=0.02,r0ω/c=50,γ =1.25,d=8,and b=2.

In Fig.3 we have seen the reliance of f1and f2on ξ for various values of αE20=0.75,1,and 1.25.The other terms are same as taken in Fig.1.Figure 3 clearly shows that with the rise of the laser beam intensity,self-focusing enhances up to great extent.The physics behind this is that with the rise in laser intensity,initial ionization of atoms in plasma as well as the strength of ponderomotive force increases.This is due to the fact that with an increase in the laser intensity the magnitude of ponderomotive force experienced by plasma electrons increases.This in turn increases the laser-induced nonlinearity of the dielectric function of plasma,as a result of which there is enhanced focusing of the laser beam.Patil et al.[29]observed the similar kind of results.They found that with the rise of the intensity parameter self-focusing becomes early and stronger.

Fig.2 Dependence f1and f2on ξ for various values of ωp0/ω.The other parameters are same as considered in Fig.1.

Fig.3 Dependence of f1and f2on ξ for various values of αE20.The other parameters are same as considered in Fig.1.

Figure 4 depicts the dependence of f1and f2on ξ for various values of b=1,1.5,and 2.Other terms are same as considered in Fig.1.Figure 4 clearly shows that sharp self-focusing happens for b=2 and for b=1 and 1.5 f first decreases and later on increases very slowly for lower values of b.All curves in the fi gure exhibit oscillatory self-focusing with substantial decrease in beam width parameter and focusing length for increase in the value of decentered parameter.Decentered parameter is an important parameter that is to be optimized for stronger self-focusing at smaller distance.This is because of the fact that the decentered parameter changes the nature of self-focusing of the beam signi fi cantly.The results we got are in good agreement with the results obtained by Gill et al.[30]

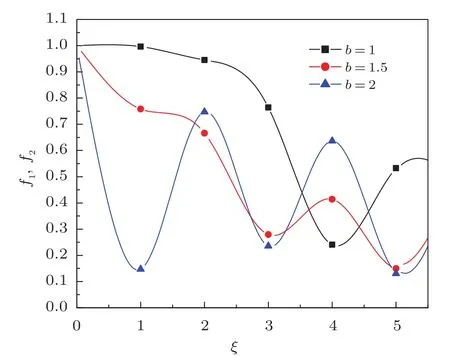
Fig.4 Dependence of f1and f2on ξ for various values of b.The other parameters are same as considered in Fig.1.

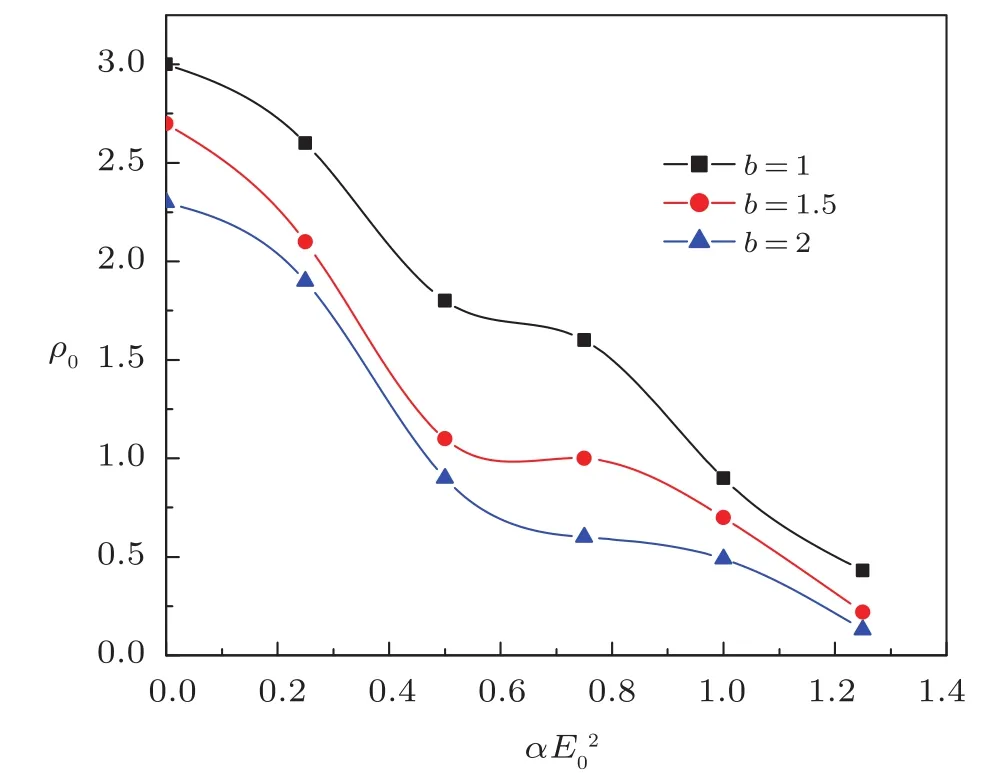
Fig.5 Dependence of ρ0(r0ωp0/c)on αE20for m0/M=0.02 and γ=1.25.

In Fig.5 dependence of initial beam width ρ0on αE20under self-trapped condition for the plasma is analyzed.Decrease in ρ0is observed with the rise in αE20for relativistic plasma at various values of the decentered parameter.

4 Conclusion

We have explored self-focusing of Hermite-cosine-Gaussian laser beam in collisionless plasma by considering relativistic nonlinearity,following WKB and paraxial approximation.Equation of the beam width parameter and self-trapped mode has been derived.Further,we have seen the influence of laser intensity,decentered parameter,and plasma density on the variation of beam width parameter as a function of normalized propagation distance.The results show that the laser beam focuses faster and occurs earlier with reduced spot size.By optimizing laser plasma parameters,spot size can be controlled.It was concluded that laser intensity and decentered parameter has a major role in the enhancement of self-focusing of Hermite cosine Gaussian laser beam in plasma.Present analysis results may be helpful in laser driven fusion.