利用端點延拓提高LS + NN模型的UT1-UTC預(yù)報精度*

趙丹寧，雷 雨,2

(1. 寶雞文理學(xué)院電子電氣工程學(xué)院，陜西 寶雞 721013；2. 中國科學(xué)院國家授時中心，陜西 西安 710600)

地球自轉(zhuǎn)運動可以用地球定向參數(shù)(Earth Orientation Parameters, EOP)表征。地球定向參數(shù)包括歲差、章動、UT1-UTC及極移的兩個分量xp與yp。地球定向參數(shù)是實現(xiàn)地球參考坐標(biāo)系與天球參考坐標(biāo)系相互轉(zhuǎn)換的必要參數(shù)，在天文地球動力學(xué)研究、衛(wèi)星導(dǎo)航及深空探測與跟蹤等領(lǐng)域均有重要作用。甚長干涉基線測量(Very Long Baseline Interferometry, VLBI)和全球衛(wèi)星導(dǎo)航系統(tǒng)(Global Navigation Satellite System, GNSS)等空間測地技術(shù)是測量地球定向參數(shù)的主要手段，其中UT1-UTC的測量精度為3～5 μs[1]，但復(fù)雜的資料處理過程致使地球定向參數(shù)的獲取存在一定的延遲。由于深空探測與跟蹤等領(lǐng)域?qū)Φ厍蚨ㄏ騾?shù)實時觀測值有重要需求，而衛(wèi)星自主導(dǎo)航又對地球定向參數(shù)中長期預(yù)報值有重要需求，因此對地球定向參數(shù)進行高精度的短期與中長期預(yù)報具有重要的現(xiàn)實意義。在地球定向參數(shù)的幾個分量中，UT1-UTC是變化最快、最難精確預(yù)報的一個分量。

當(dāng)前預(yù)報UT1-UTC的方法有多種，其中多數(shù)方法聯(lián)合最小二乘(Least-squares, LS)外推和神經(jīng)網(wǎng)絡(luò)(Neural Network, NN)或自回歸(Autoregressive, AR)等模型進行預(yù)報[2-3]。這些方法的思路為，首先采用最小二乘外推模型提取UT1-UTC序列中的周期項，并對周期項進行外推，然后利用神經(jīng)網(wǎng)絡(luò)或自回歸等模型對最小二乘擬合殘差進行建模、預(yù)報，最后再將周期項和殘差項的外推值相加得到UT1-UTC的預(yù)報值。在預(yù)報實踐中發(fā)現(xiàn)，利用最小二乘外推模型對UT1-UTC觀測資料進行擬合時，在擬合序列的兩端存在發(fā)散畸變現(xiàn)象，這種現(xiàn)象在數(shù)據(jù)處理中稱為端部效應(yīng)[4-5]。端部效應(yīng)使殘差項、周期項的預(yù)報值出現(xiàn)偏差，最終導(dǎo)致UT1-UTC的預(yù)報值不準(zhǔn)確。

本文針對UT1-UTC預(yù)報中最小二乘擬合出現(xiàn)的端部畸變現(xiàn)象，在采用最小二乘外推模型對UT1-UTC觀測資料進行擬合之前，先利用灰色模型對UT1-UTC觀測資料進行數(shù)據(jù)延拓，即在UT1-UTC序列的兩端增加應(yīng)用灰色模型延拓的若干數(shù)據(jù)點，形成一個新序列，然后利用最小二乘外推模型對新序列進行擬合，最后再聯(lián)合最小二乘外推模型和神經(jīng)網(wǎng)絡(luò)(LS + NN)對原始UT1-UTC序列外推，這樣就可以將最小二乘擬合出現(xiàn)的端部畸變現(xiàn)象移至新序列的兩端。數(shù)值分析表明，通過在UT1-UTC序列兩端增加統(tǒng)計延拓數(shù)據(jù)，可以有效地抑制最小二乘擬合出現(xiàn)的端部效應(yīng)現(xiàn)象，并且可以顯著提高預(yù)報精度。

1 端點延拓算法

灰色模型可以在系統(tǒng)變化規(guī)律不明確的情況下利用少量的已知信息推知系統(tǒng)的發(fā)展趨勢，且預(yù)測精度高、建模簡單。一方面，灰色模型可以利用較少的觀測數(shù)據(jù)進行UT1-UTC序列的端點外推延拓，所外推的序列在一定程度上反映UT1-UTC序列的整體變化趨勢[6]；另一方面，基于端點延拓算法形成的UT1-UTC新序列僅用來求解最小二乘模型系數(shù)，目的是將最小二乘擬合出現(xiàn)的端部效應(yīng)移至新序列的兩端，而兩端序列并不參與UT1-UTC預(yù)報[7]。因此，基于灰色模型的端點延拓算法用于改善最小二乘擬合的端部效應(yīng)是完全可行的。

灰色模型建模的基本思路為，首先利用少量原始觀測值通過累加生成操作(Accumulated Generating Operation, AGO)生成一次累加序列，然后利用此累加序列建立相應(yīng)的離散預(yù)測模型，并獲得累加序列的預(yù)測值，最后再通過累減生成操作(Inverse Accumulated Generating Operation, IAGO)獲得原始序列的預(yù)測值。灰色預(yù)報模型GM(1, 1)的一般形式：

x^(k+p)=[x(1)-u/a]e-a(k+p-1)(1-ea),

(1)

其中，u，a為灰色模型系數(shù)；k為參與建模的原始觀測值個數(shù)；p為預(yù)報跨度。設(shè)X={x(1),x(2), …,x(n)}為原始離散序列，則灰色模型端點延拓算法如下：

(1)對于原始離散序列X的左端，在左端點處取k個觀測值，其反序列為

X1={x(k),x(k-1),…,x(1)}，

(2)

將X1作為左端建模序列進行灰色預(yù)測，得到預(yù)測序列：

X2={x^(0),x^(-1),…,x^(1-p)}，

(3)

則X2的反序列，即原始離散序列X的左端點延拓序列為

X3={x^(1-p),x^(2-p),…,x^(0)}.

(4)

(2)對于原始離散序列X的右端，在右端點處取k個觀測值，得到序列X4：

X4={x(0)(n-k+1),x(0)(n-k+2),…,x(0)(n)}，

(5)

將X4作為右端建模序列進行灰色預(yù)測，得到預(yù)測序列：

X5={x^(n+1),x^(n+2),…,x^(n+p)}，

(6)

將序列X3，X5分別作為原始離散序列X的左、右端點延拓值，得到延拓后的離散序列：

X′={x^(1-p),…,x^(0),x(1),…,x(n),x^(n+1),…,x^(n+p)}.

(7)

2 預(yù)報模型

2.1 最小二乘外推模型

UT1-UTC序列中的長期趨勢項、周年項及半年項利用如下模型進行擬合：

(8)

其中，ω1，ω2分別為周年項和半年項的振蕩角頻率，取ω1=2π/365.24，ω2=2π/182.62[4]；γ，β，di和ei為未知參數(shù)，可通過最小二乘法求解。

2.2 神經(jīng)網(wǎng)絡(luò)模型

提取長期趨勢項和周期項后的最小二乘擬合殘差序列中含有剩余的短周期成分，也含有非線性成分，對于這些成分，利用神經(jīng)網(wǎng)絡(luò)進行建模較為合理。對于最小二乘擬合殘差序列{ε(t),t=1, 2, …,n}，假設(shè)t時刻的殘差值ε(t)可由t-1,t-2, …,t-m時刻的歷史殘差值ε(t-1),ε(t-2), …,ε(t-m)進行預(yù)測，可建立從輸入模式到輸出模式的數(shù)據(jù)映射f：Rm→R，預(yù)測模型可表示為

ε(t)=f([ε(t-1),ε(t-2),…,ε(t-m)])，

(9)

其中，m為嵌入維數(shù)。本文采用極限學(xué)習(xí)機(Extreme Learning Machine, ELM)算法訓(xùn)練神經(jīng)網(wǎng)絡(luò)[8]，從而建立從輸入模式到輸出模式的數(shù)據(jù)非線性映射。在殘差預(yù)報過程中，當(dāng)已經(jīng)預(yù)報出一部分殘差值的情況下，后面的殘差是根據(jù)其對應(yīng)的歷元通過移動窗口的方法獲得[9]。

2.3 預(yù)報流程

本文模型與常規(guī)最小二乘加神經(jīng)網(wǎng)絡(luò)模型的差別之處在于，本文模型在對UT1-UTC序列進行最小二乘擬合之前，先應(yīng)用灰色模型在UT1-UTC序列兩端進行數(shù)據(jù)延拓，然后再對延拓后的UT1-UTC序列進行最小二乘擬合，建立周期項和趨勢項最小二乘外推模型，最后利用最小二乘加神經(jīng)網(wǎng)絡(luò)模型對原始UT1-UTC序列進行預(yù)報。值得說明的是，在對UT1-UTC序列進行外推之前，需要根據(jù)國際地球自轉(zhuǎn)與參考系服務(wù)(International Earth Rotation and Reference Systems Service, IERS)協(xié)議扣除UT1-UTC序列中周期為5 d～18.6 a的62個固體地球帶諧潮汐項[10]，同時還必須扣除閏秒。將本文提出的模型稱之為端部效應(yīng)改善的最小二乘加神經(jīng)網(wǎng)絡(luò)(Edge-effect Corrected LS + NN，ECLS + NN)模型，預(yù)報流程如圖1。

圖1 端部效應(yīng)改善的最小二乘加神經(jīng)網(wǎng)絡(luò)模型的預(yù)報流程
Fig.1 Flowchart of the ECLS + NN prediction model

3 模型驗證

3.1 數(shù)據(jù)來源

本文試驗所用的UT1-UTC數(shù)據(jù)來自IERS發(fā)布的EOP 08 C04序列，時間跨度為2000-01-01～2016-10-01，采樣間隔為1 d。

3.2 精度評定標(biāo)準(zhǔn)

為了衡量UT1-UTC預(yù)報結(jié)果的精度，選用平均絕對誤差(Mean Absolute Error, MAE)作為精度評定標(biāo)準(zhǔn)，其計算公式為

(10)

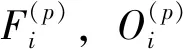
3.3 結(jié)果分析

選取2001-01-01～2016-09-20期間的UT1-UTC觀測資料進行試驗分析，其中2010-01-01～2016-09-20為預(yù)測期，建模數(shù)據(jù)長度為10 a，每隔7 d預(yù)報1次，總共進行了300次預(yù)測。

為了驗證端點延拓方法對最小二乘擬合端部效應(yīng)的改善效果，首先對比端點延拓前后最小二乘擬合效果。圖2分別繪出了端點數(shù)據(jù)延拓前后最小二乘擬合序列左、右端360個歷元的擬合殘差數(shù)據(jù)點，擬合時段為2002-01-01～2011-12-31，其中，端點數(shù)據(jù)延拓個數(shù)為240，即在UT1-UTC觀測序列的左、右兩端各延拓120個數(shù)據(jù)點。從圖2可以看出，與直接對UT1-UTC原始序列進行擬合相比，基于灰色模型端點延拓后的UT1-UTC序列在左、右兩端最小二乘擬合的殘差值更小，這說明端點延拓方法可以提高最小二乘模型在UT1-UTC序列左、右兩端的擬合準(zhǔn)確性，從而抑制最小二乘擬合序列出現(xiàn)的端部效應(yīng)現(xiàn)象。

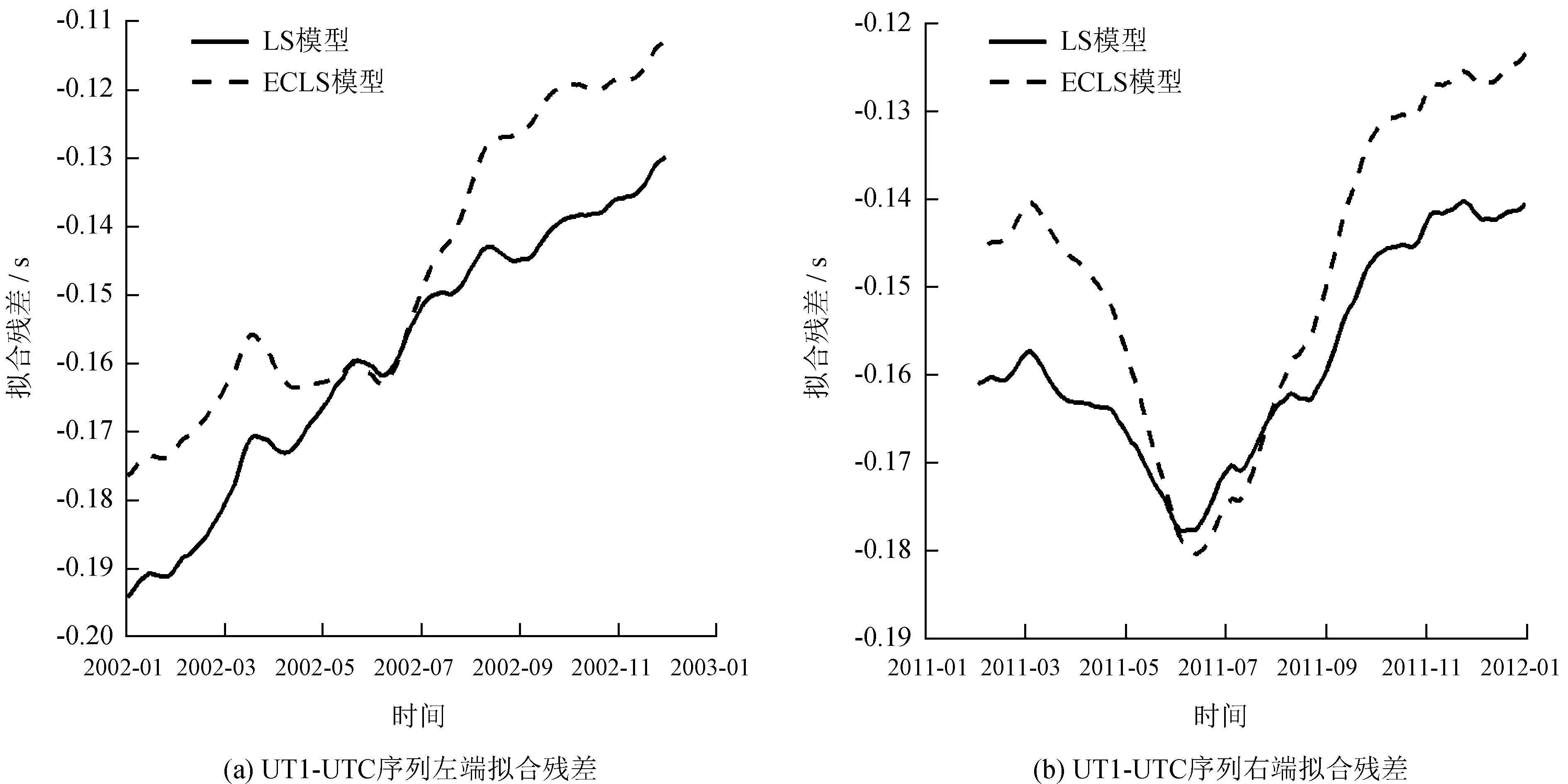
圖2 最小二乘和端部效應(yīng)改善的最小二乘模型在UT1-UTC序列左、右兩端的擬合殘差
Fig.2 LS and ECLS fitting residuals of the UT1-UTC time-series at boundaries

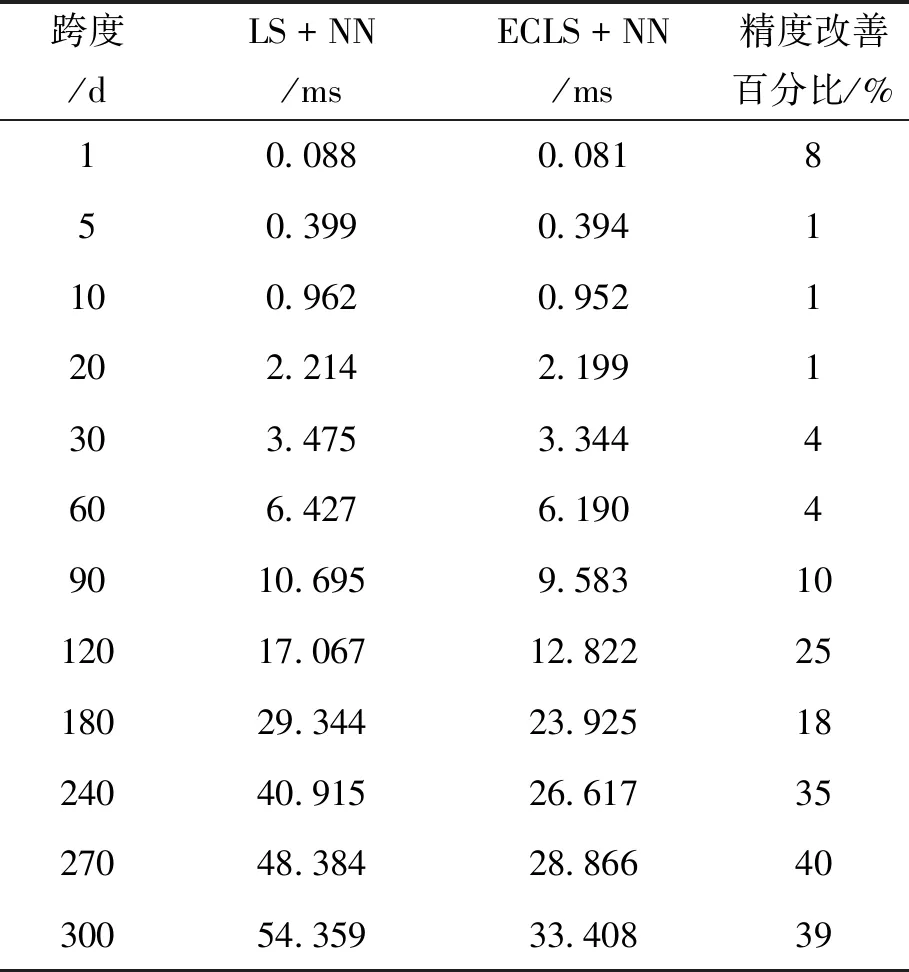
為了進一步檢驗基于灰色模型的端點延拓方法對最小二乘加神經(jīng)網(wǎng)絡(luò)模型預(yù)報UT1-UTC的改善效果，本文分別利用最小二乘加神經(jīng)網(wǎng)絡(luò)模型與端部效應(yīng)改善的最小二乘加神經(jīng)網(wǎng)絡(luò)模型對UT1-UTC進行1～300 d的預(yù)報，圖3繪出了最小二乘加神經(jīng)網(wǎng)絡(luò)模型和端部效應(yīng)改善的最小二乘加神經(jīng)網(wǎng)絡(luò)模型UT1-UTC預(yù)報結(jié)果的平均絕對誤差曲線，表1統(tǒng)計了最小二乘加神經(jīng)網(wǎng)絡(luò)模型和端部效應(yīng)改善的最小二乘加神經(jīng)網(wǎng)絡(luò)模型在不同預(yù)報長度下的平均絕對誤差值。從圖3與表1可以發(fā)現(xiàn)，端部效應(yīng)改善的最小二乘加神經(jīng)網(wǎng)絡(luò)模型相對于最小二乘加神經(jīng)網(wǎng)絡(luò)模型的UT1-UTC預(yù)報精度在各個跨度都有不同程度的提高，其中，對于跨度為1～90 d的預(yù)報，精度提高在10%以內(nèi)；從第90 d開始，端部效應(yīng)改善的最小二乘加神經(jīng)網(wǎng)絡(luò)模型的預(yù)報精度提高越來越顯著，最大提高達40%，這說明端部效應(yīng)改善的最小二乘加神經(jīng)網(wǎng)絡(luò)模型對于UT1-UTC中長期預(yù)報精度改進更為顯著。

表1 最小二乘加神經(jīng)網(wǎng)絡(luò)模型和端部效應(yīng)改善的最小二乘加神經(jīng)網(wǎng)絡(luò)模型不同跨度UT1-UTC預(yù)報結(jié)果的平均絕對誤差統(tǒng)計

Table 1 MAE statistics of the UT1-UTC predictions by the LS + NN and ECLS + NN models

跨度/dLS+NN/msECLS+NN/ms精度改善百分比/%10.0880.081850.3990.3941100.9620.9521202.2142.1991303.4753.3444606.4276.19049010.6959.5831012017.06712.8222518029.34423.9251824040.91526.6173527048.38428.8664030054.35933.40839

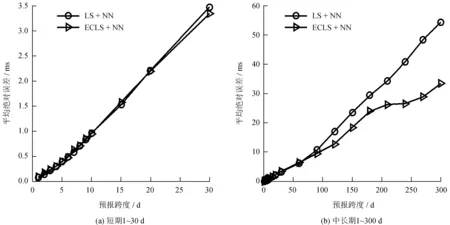
圖3 最小二乘加神經(jīng)網(wǎng)絡(luò)模型和端部效應(yīng)改善的最小二乘加神經(jīng)網(wǎng)絡(luò)模型UT1-UTC預(yù)報結(jié)果的平均絕對誤差比較

Fig.3 MAE comparison between the LS + NN and ECLS + NN models for the UT1-UTC predictions

4 結(jié)果分析

本文提出了一種利用端點延拓改善最小二乘擬合序列端部效應(yīng)的方法，該方法在對UT1-UTC序列進行最小二乘擬合之前，首先在UT1-UTC序列兩端增加統(tǒng)計延拓數(shù)據(jù)，然后再對數(shù)據(jù)延拓后的新序列進行最小二乘擬合，目的是將最小二乘擬合存在的端部畸變移至新序列的兩端，從而抑制原始擬合序列的端部畸變。試驗結(jié)果表明，通過在UT1-UTC觀測序列的兩端增加用灰色模型延拓出的外推數(shù)據(jù)點，然后再進行最小二乘擬合，能夠有效地抑制端部效應(yīng)的影響。與常規(guī)最小二乘加神經(jīng)網(wǎng)絡(luò)預(yù)報模型相比，端部效應(yīng)改善的最小二乘加神經(jīng)網(wǎng)絡(luò)模型的UT1-UTC預(yù)報精度在各種跨度均有不同程度的提高，其中跨度為中長期預(yù)報的精度提升尤為明顯，因此端部效應(yīng)改善的最小二乘加神經(jīng)網(wǎng)絡(luò)模型更適用于UT1-UTC中長期預(yù)報。