基于壓縮感知法對法拉第色散函數的重構*

于衍川，孫曉輝

(云南大學物理與天文學院，云南 昆明 650500)

法拉第旋轉(Faraday Rotation)是線偏振電磁波通過磁化星際介質時偏振角發生旋轉的一種物理現

(1)

其中，ne為熱電子密度；B‖為視線方向的磁場分量；dl是視線方向上的線元。這樣觀測到的偏振量P可以寫成[1]：

P(λ2)=Q(λ2)+iU(λ2)

(2)

(3)

其中，F(φ)為法拉第色散函數(Faraday Dispersion Function)，是法拉第深度的函數；Q和U為斯托克斯參量，是觀測波長(頻率)的函數。從(3)式可以看出，偏振量P和法拉第色散函數F(φ)之間是傅里葉變換對。F(φ)表示法拉第深度為φ處的偏振強度和偏振位置角，反映輻射區域以及輻射傳播途徑上的磁場結構。為了研究星際介質的磁場，需要重構法拉第色散函數。目前已有多種重構法拉第色散函數的方法。文[1]提出了法拉第旋率綜合方法(Faraday Rotation Measure Synthesis, RMS)，通過觀測偏振量和法拉第色散函數之間的傅里葉關系重構法拉第色散函數。因為觀測波段是有限的，所以獲得的法拉第色散函數是真實色散函數與窗口函數的卷積，對復雜的源需要解卷積。與法拉第旋率綜合方法類似的還有小波方法[2-3]。此外，還有一些假定輻射模型的方法重構法拉第色散函數，如Q-U擬合法[4]。

本文主要討論壓縮感知方法(或稱為壓縮采樣，Compressive Sensing/Sampling，原理見[5-6])。該方法的優點在于利用極少的采樣數據也有可能重構原始的完整信號。壓縮感知理論以信號的稀疏性為前提，通過編碼測量和重構算法實現信號的精確重構。目前，已經提出了基于壓縮感知法的法拉第色散函數重構算法，如文[7]采用最小l1范數法建立了適用于法拉第薄源(Faraday Thin，λ2Δφ? 1，這里Δφ為源在法拉第深度域上的延展范圍，即F(φ)的寬度)、法拉第厚源(Faraday Thick,λ2Δφ? 1)和同時含有法拉第薄源和法拉第厚源的算法，模擬結果顯示，該方法可以用于重構法拉第色散函數，并與法拉弟旋率綜合方法進行比較，發現用壓縮感知方法重構的法拉第色散函數在數值和誤差上要優于法拉弟旋率綜合方法。文[8]采用匹配追蹤算法建立了對同時含有法拉第薄源和法拉第厚源進行重構的方法。但這些方法目前還處于理論模擬階段，其實用性還有待研究，比如文[7]的算法中設置的頻率(波長)范圍過大，未將噪聲添加到實驗數據中，算法中各種參數設置對重構結果的影響也沒有進行實驗和討論以及實驗樣本過少等。本文基于文[7]的方法，從實際觀測角度進行數值模擬，對以上問題進行更深入研究，以此探討其實用性。這里假定法拉第色散函數是稀疏的(即針對源包含一個或多個法拉第薄成分)，用Python語言編寫了重構法拉第色散函數的程序。采用的頻率范圍為1.1～3.1 GHz，對應澳大利亞望遠鏡致密陣(Australia Telescope Compact Array, ATCT)上L波段的觀測頻率范圍[9]。

1 重構方法

已知測量矩陣A∈RM × N(M?N)和未知信號x0在該矩陣的線性投影y∈RM，即y=Ax0，要由測量值y重構未知信號x0。在壓縮感知理論中，假定未知信號x0為稀疏的，信號x0可以由測量值y通過求解最小l1范數問題精確重構：

x=min‖x0‖l1s.t.Ax0=y.

(4)

若未知信號x0為非稀疏的，可以通過某種變換(如小波變換)進行稀疏性表示，即x0=ωX，X為該信號在ω變換域下的稀疏性表示，則有

x=min‖X‖l1s.t.Ax0=AωX=y.

(5)

將(2)式寫成矩陣形式：

Yf=P，

(6)

其中，f為法拉第色散函數，是一個N維矢量；Y為P和f之間傅里葉變換的離散表示，是一個M×N矩陣；P為觀測偏振量，是一個M維矢量，這里M為觀測頻率通道數，每個通道上接收不同波段的偏振量。

由于法拉第色散函數f是復變函數，可以將其實部和虛部分別寫成f.real和f.imag，則(6)式可變為

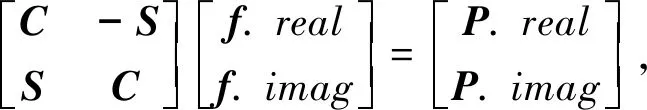
(7)

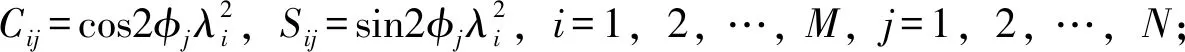
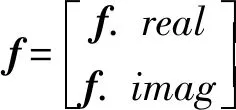
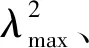
(8)

(9)

實驗中，將均值為0、標準差σ為1(強度單位任意，下同)的高斯噪聲加到Q和U上，并設置在法拉第深度φ空間的分辨率δφ為ΔφFWHM的1/4，則總的格點數N(φ空間中坐標點φi的個數，i=1, 2, …,N)為

(10)

其中，int()表示取整。表1列出了一些主要的實驗參數。

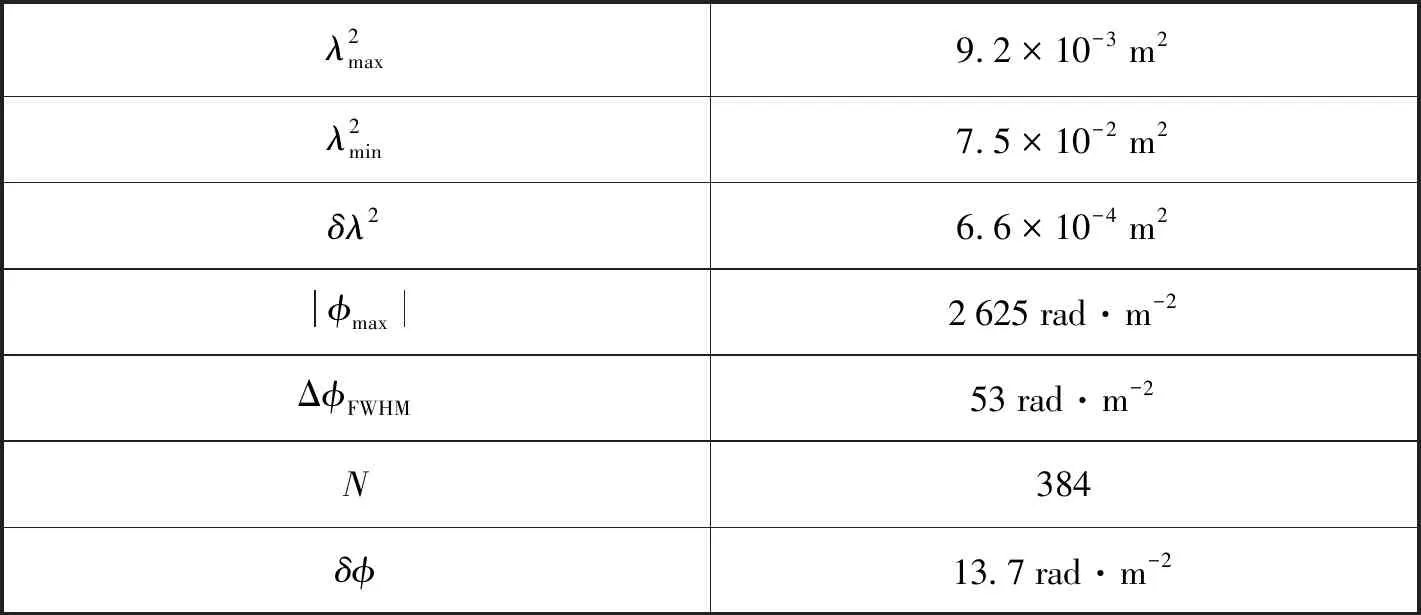
表1 實驗參數Table1 Experimental parameters

2 結果與討論

2.1 一般情況

在模擬實驗中，假定一個法拉第色散函數包含5個法拉第薄源,這些源分別是：F(-164.1)=3 + 6i，F(-82.0)=-4 + 3i，F(0.0)=2 + 3i，F(68.4)=-8 - 5i，F(136.7)=5 + 3i，對應的信噪比分別為：6.7， 5.0， 3.6， 9.4， 5.8。對包含這5個法拉第薄源的法拉第色散函數進行了反解，結果如圖1(a)，

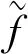
(11)

其中，p為偏振強度。從圖1可以看出，沒有噪聲時該模型準確地重構了原始圖像，而加入噪聲時，重構結果出現了偏差，|dwm|分別為5.80 × 10-5，11.78。

通過壓縮感知方法重構的法拉第色散函數隨著法拉第薄源偏振強度的大小、相位以及兩個法拉第薄源的法拉第深度之間間隔Δφ的不同而不同，甚至不能準確地重構出原始圖像。在這里分兩種情況進行測試說明：(1)假定上述5個法拉第薄源的法拉第深度之間的間隔Δφ不變，改變其大小和相位，如F(-164.1)=3 - 6i，F(-82.0)=-4 + 3i，F(0.0)=5 + 3i，F(68.4)=8 - 5i,F(136.7)=-5 + 4i，對應的信噪比分別為：6.7，5.0，5.8，9.4，6.4，重構結果如圖1(b)；(2)假定大小和相位不變，改變其法拉第深度之間的間隔Δφ，如：F(-150.4)=3 + 6i，F(-68.4)=-4 + 3i，F(0.0)=2 + 3i，F(109.4)=-8 - 5i，F(164.1)=5 + 3i，對應的信噪比分別為6.7，5.0，3.6，9.4，5.8，重構結果如圖1(c)。

當假定間隔Δφ不變時，從圖1可以看出，前3個源并沒有很好地重構出原始圖像，其相位和大小存在一定誤差，其中，|dwm|分別為6.31，17.03。而假定大小和相位不變時，后面4個源都與原始圖像出現了較大偏差，其中，|dwm|分別為8.18，17.11。同時也發現，在不加入噪聲時，將這些法拉第薄源的法拉第深度之間的間隔Δφ設置得足夠大時，即Δφ> 90 rad·m-2時，無論改變其大小、相位還是間隔Δφ，該模型均能準確地重構原始圖像，即使在加入噪聲時，產生的誤差也很微小。當然，以上測試的這些源的法拉第深度都是設置在該方法的格點N上進行的。

通常，在實際應用中，事先并不知道法拉第色散函數的法拉第深度以及兩個源的法拉第深度之間的間隔Δφ，要重構的法拉第色散函數各個成分的法拉第深度是隨機的，一般不在這種方法設置的格點N上，并且Δφ也是隨機的，所以也無法確定該模型是否能夠很好地重構法拉第色散函數。隨機選取一個包含5個法拉第薄源的色散函數(這些法拉第薄源的法拉第深度不在格點N上)：F(-114)=-6 - 1i，F(-60)=7 - 4i，F(48)=3 - 5i，F(102)=-3.5 + 3i，F(210)=9 + 3i，對應的信噪比分別為：6.1，8.1，5.8，4.6，9.5。其測試結果如圖1(d)， 其中，|dwm|分別為0.40，10.20。

每次模擬都是隨機產生的高斯噪聲，所以每次重構的結果不同。在實驗中，對于法拉第色散函數的重構結果隨著源的個數、大小、相位和噪聲的不同出現不同程度的誤差，同時也與該方法中設置的參數有關，如觀測通道M，φ空間的分辨率δφ。

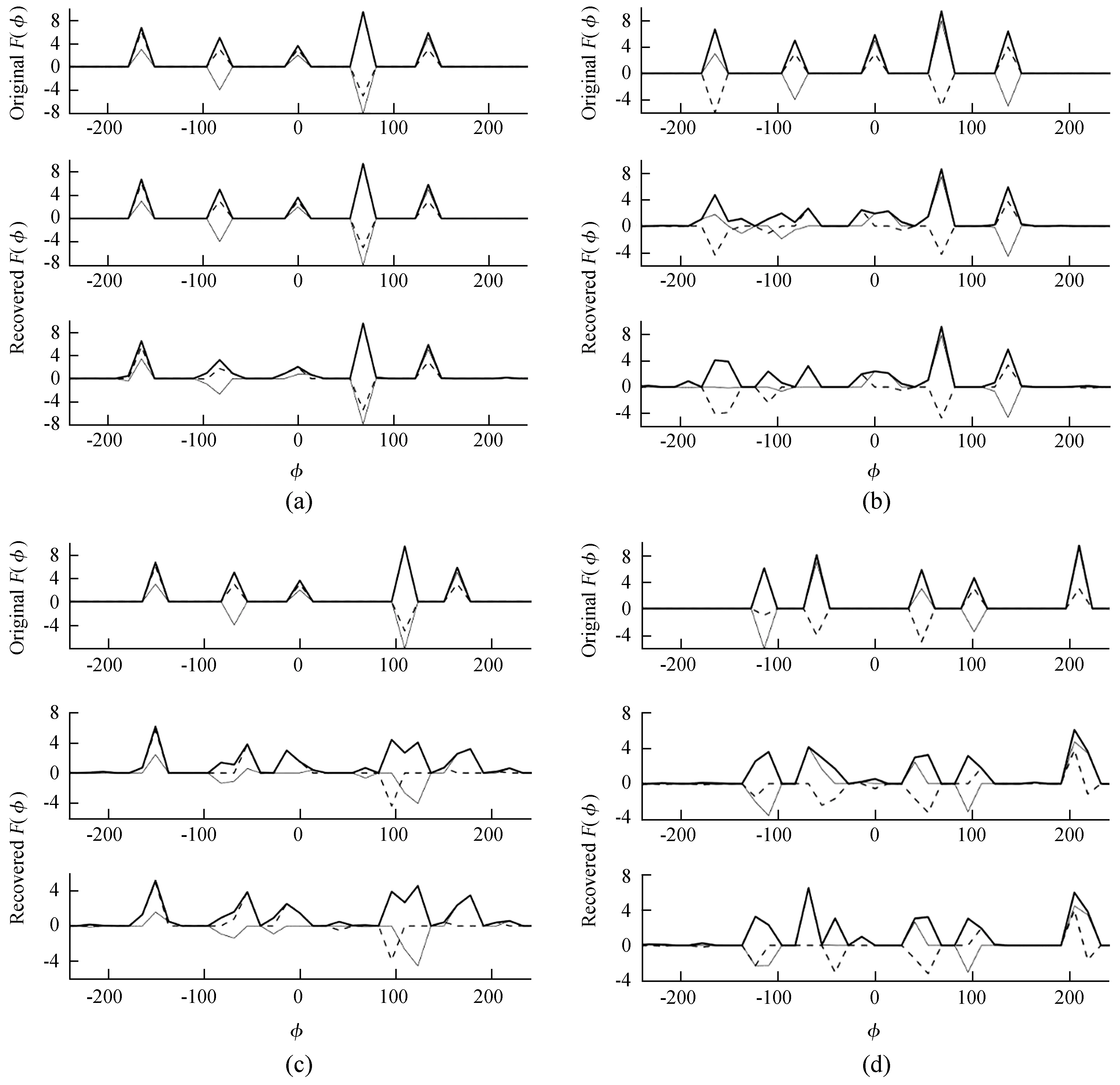
圖1 法拉第色散函數的重構結果。每幅圖從上往下，上圖為原始數據，中圖為無噪聲重構結果，下圖為有噪聲重構結果，粗實線表示振幅，細實線表示實部，細虛線表示虛部

Fig.1 The reconstruction result of Faradqy dispersion function. From top to bottom in each panel: the original data, the noiseless reconstruction result and the with-noise reconstruction result. The thick solid line shows the amplitude, the thin solid line as real part, the dashed line as imaginary part

2.2 大樣本實驗

為了更直觀地觀察該方法的重構效果，從噪聲、兩個源的法拉第深度之間的間隔Δφ、φ空間的分辨率δφ(δφ的不同會導致總的格點數N不同)3方面對重構結果的影響分別進行了大樣本統計學實驗。以重構的源的數目和φ的加權平均的差值描述重構結果的好壞[10]。

首先考察信噪比對重構結果的影響，這里假定法拉第色散函數只包含一個法拉第薄源，固定其法拉第深度為φ=20 rad·m-2，隨機模擬了1 000個信噪比范圍在(3, 60)之間的源(這里噪聲依然設置為1，信噪比相當于法拉第色散函數的偏振強度)，φ空間的分辨率δφ依然為ΔφFWHM的1/4，由于只含有一個法拉第薄源，直接以φ的差值|φrecorved-φoriginal|描述重構效果，并排除信噪比小于2的信號。結果如圖2(a)。從圖中可以看出，對于含有一個源的情況，可以很準確地重構出源的數目，而φ的差值總是在兩個值上，即重構的φrecorved出現在相鄰的兩個格點上。為了減小重構誤差，對重構結果在峰值附近進行最小二乘擬合，結果如圖2(b)。經過擬合后，對于大多數源來說，φ的差值縮小為原來的1/2～1/4。由于重構的法拉第深度φ總在相鄰的兩個格點上，是否也可以通過縮小φ空間分辨率的方式減小φ的重構誤差呢？

圖2 從左到右為 (a) 無擬合；(b) 擬合后。每幅圖從上往下，上為重構數目，下為φ的差值

Fig.2 From left to right: (a) no fitting; (b) fitting. From top to bottom in each panel:the number of reconstructions, the difference ofφ

下面考查兩個源的法拉第深度之間的間隔Δφ和φ空間的分辨率δφ對重構結果的影響。假定一個法拉第色散函數包含2個法拉第薄源，固定其中一個源的偏振強度p=13.235，偏振位置角χ=2.749，法拉第深度φ=10.256 rad·m-2。第2個源是隨機模擬了1 000個偏振強度在(3, 30)、偏振位置角在(0, 2π)、間隔Δφ在(5, 200)之間的源。同時，對不同分辨率δφ的情況(即δφ取ΔφFWHM的1/2，1/3，1/4，1/5，1/6，1/7，1/8，1/9)分別進行以上實驗，這里排除信噪比小于1的信號。結果如圖3。

為了比較不同分辨率情況下的重構效果，對不同分辨率下準確重構出源的數目的精確度進行了比較，如圖4。從圖4可以看出，當δφ取ΔφFWHM的1/3和1/4時，精確度最高，達到83%左右。在以上對噪聲影響的實驗時，曾提出是否可以通過縮小分辨率的方式減小重構誤差的問題，而在這個實驗中可以看出，分辨率δφ并不是越小越好。

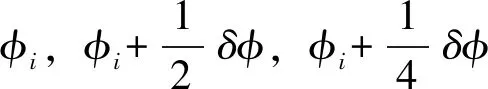
圖3 不同分辨率下間隔Δφ對重構結果的影響。第1排從左到右為(a)δφ取ΔφFWHM的1/2；(b)δφ取ΔφFWHM的1/3；第2排從左到右為 (c)δφ取ΔφFWHM的1/4；(d)δφ取ΔφFWHM的1/5；第3排從左到右為 (e)δφ取ΔφFWHM的1/6；(f)δφ取ΔφFWHM的1/7；第4排從左到右為(g)δφ取ΔφFWHM的1/8；(h)δφ取ΔφFWHM的1/9。每幅圖從上往下，上為重構數目，下為φ的加權平均的差值dwm

Fig.3 Influence of the interval Δφat different resolutions. From left to right in first row: (a)δφtakes 1/2 of ΔφFWHM; (b)δφtakes 1/3 of ΔφFWHM, in second row: (c)δφtakes 1/4 of ΔφFWHM; (d)δφtakes 1/5 of ΔφFWHM, in third row: (e)δφtakes 1/6 of ΔφFWHM; (f)δφtakes 1/7 of ΔφFWHM, in fourth row: (g)δφtakes 1/8 of ΔφFWHM; (h)δφtakes 1/9 of ΔφFWHM. From top to bottom in each panel: the number of reconstructions, the difference (dwm) of the weighted average ofφ

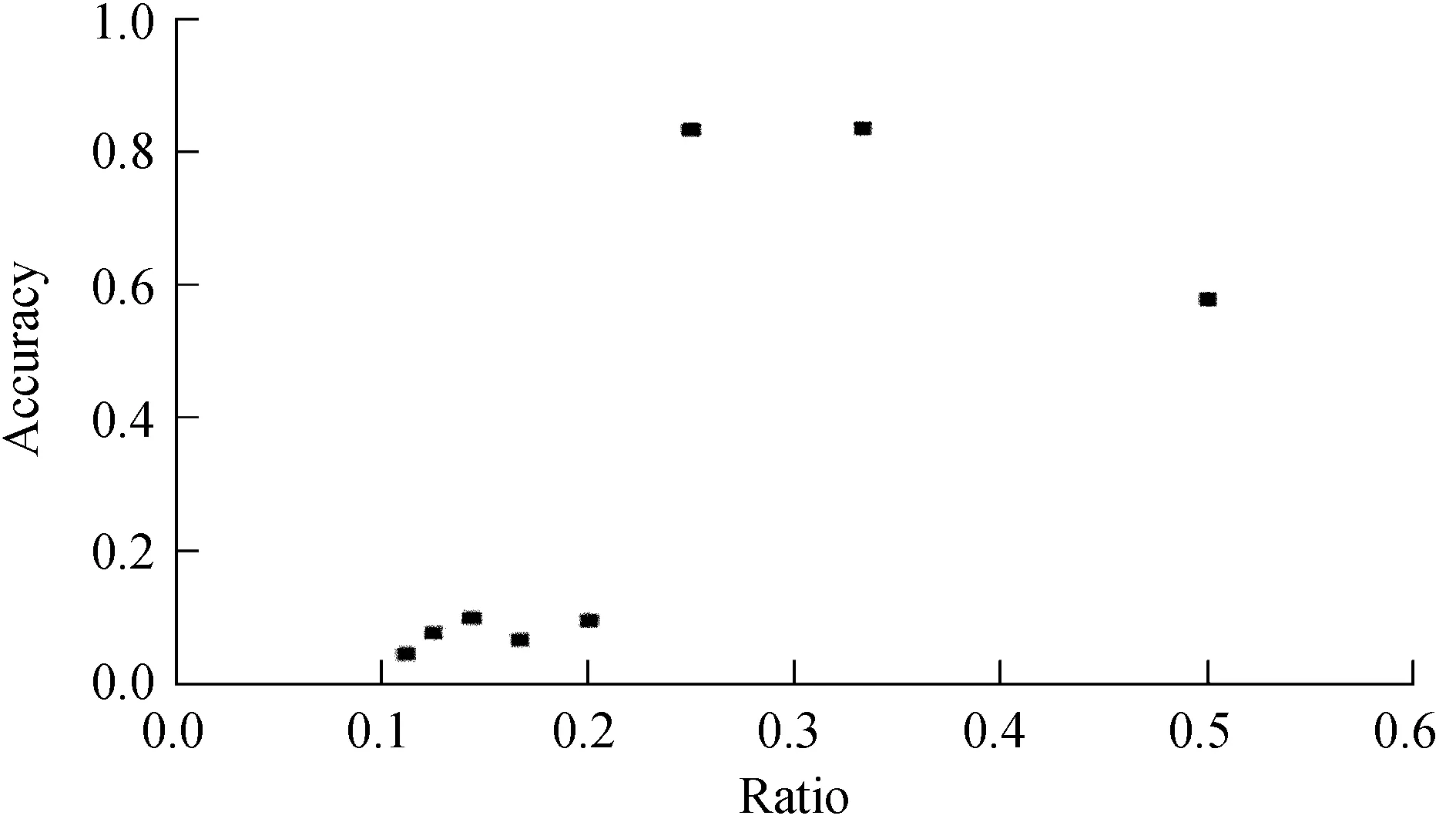
圖4 不同分辨率下的重構精度比較。x軸表示δφ/ΔφFWHM的比值，y軸表示重構數目的精確度

Fig.4 Comparison of reconstruction accuracy at different resolutions.X-axis represents the ratio ofδφ/ΔφFWHM,andY-axis represents the accuracy of the number of reconstructions

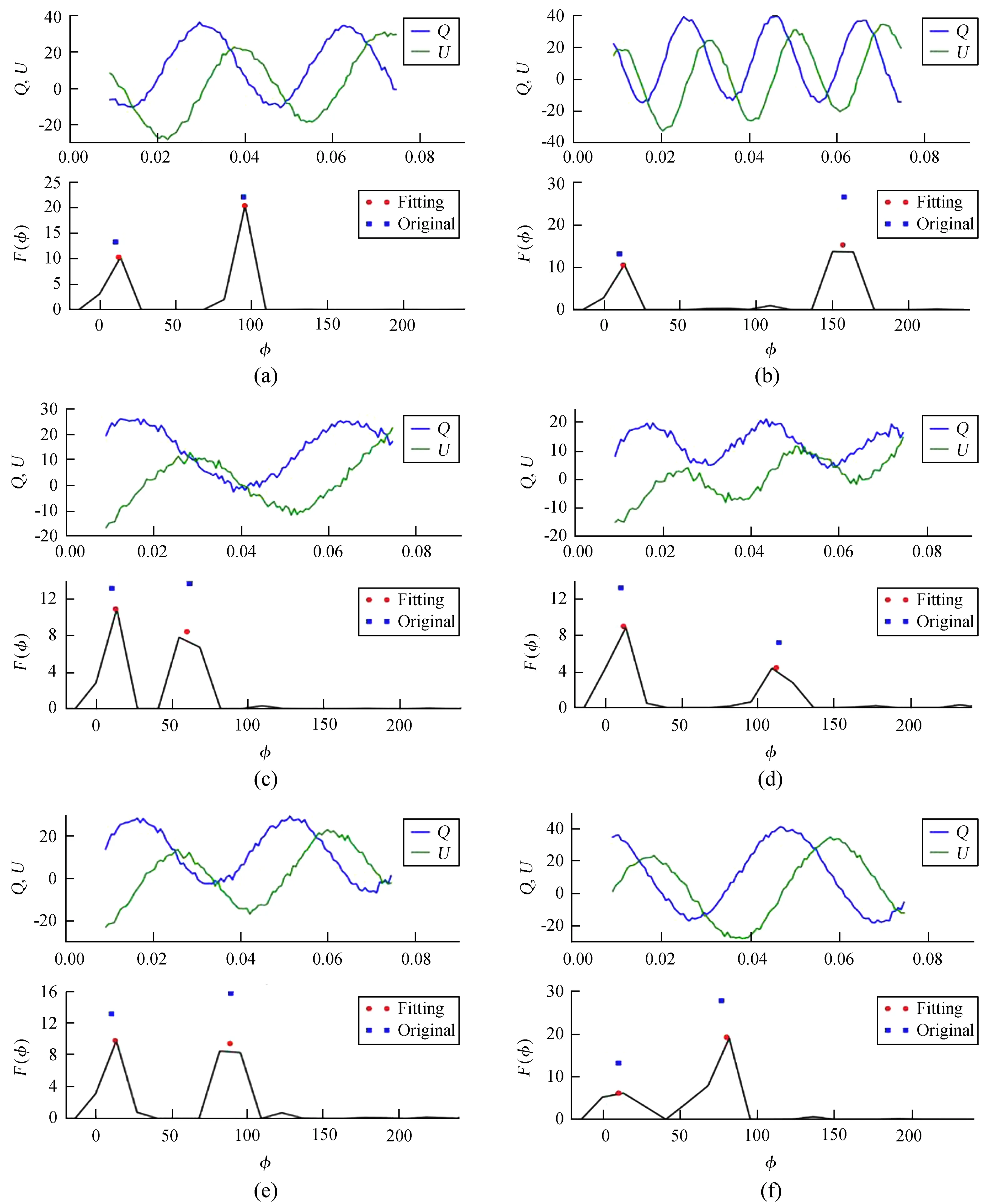
圖5 以δφ取ΔφFWHM的1/4時實驗為例，隨機選取的重構圖像
Fig.5 Examples of reconstructed images, whenδφtakes 1/4 of ΔφFWHM

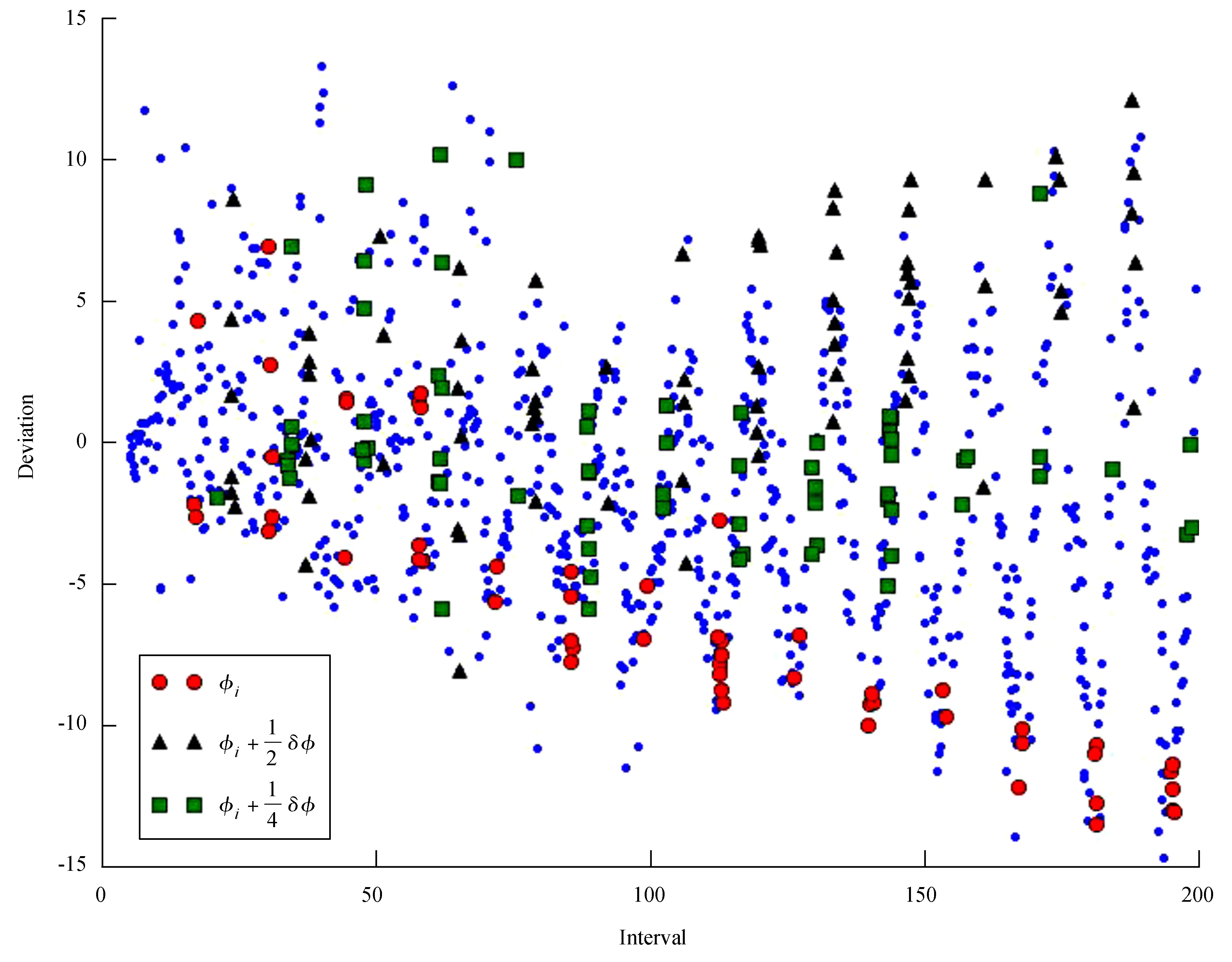
圖6dwm隨著間隔Δφ的變化
Fig.6 This picture showsdwmvaries with Δφ

3 結 論

在多個頻率上測量彌漫射電輻射的偏振是研究銀河系磁場的一種有效的方法。目前的法拉第旋率綜合法是利用偏振強度與法拉第色散函數之間是傅里葉變換對，把觀測到的偏振強度做傅里葉逆變換得到法拉第色散函數[1]。因受觀測波段的限制，得出的解需要進行解卷積，所以需要一種更強有力的方法解決這一問題。

本文基于壓縮感知的法拉第色散函數重構方法應用到實際觀測頻率范圍中，并對可能影響該方法重構效果的因素分別進行了實驗。實驗結果表明，該方法的重構效果隨著法拉第薄源的個數、源偏振強度的大小、相位以及兩個法拉第薄源的法拉第深度之間間隔Δφ的不同而出現較大差異，具有較大的隨機性。大樣本統計學實驗發現，當φ空間的分辨率δφ取ΔφFWHM的1/3和1/4時，重構結果精確度最高，對其重構結果各峰值附近再次進行最小二乘擬合后得到的法拉第深度φ值更接近原始值。通過壓縮感知法重構后的再次擬合，可以得到更為精確的法拉第深度φ值，因此該方法可以作為現有方法的一種補充，同時該方法對于重構得出的偏振強度普遍偏低，重構效果具有較大的隨機性，所以，還需要不斷地改進，提高其穩定性和精確度，以便更好地應用于實際觀測數據中。