基于ANSYS的塔器自振周期計算

李俊儒

(中石化寧波工程有限公司，上海 200030)

自振周期(或頻率)是塔器設計中確定風載、地震載的重要參數，它直接影響著塔器動力計算結果的精度。對于常見的自支承式塔，在確定其自振特性時，可視為一端固定、另一端自由的懸臂梁【1】，從而將問題轉化為求解懸臂梁的線性振動。

目前，NB/T 47041—2014《塔式容器》【2】中自振周期主要的計算方法包括：1)彈性連續體解析法，即NB/T 47041中的式(19)，為精確解法，但只適用于等截面塔；2)集中質量法，即NB/T 47041中的式(16)，需要事先假定振型函數，對于復雜結構和高振型計算困難；3)矩陣迭代法，即NB/T 47041中的附錄B，求解高振型時通常采用此法，計算相對復雜。

而有限元法汲取了集中質量法與假設模態法的優點，它將實際結構劃分為一系列離散單元，單元之間通過節點連接，然后對這些單元的組合體進行求解【3】。有限元法可根據塔器的截面變化、加載及支座等情況，劃分單元并賦予其相應的截面特性、材料屬性以及施加約束、載荷，是不等截面塔器自振特性分析的有力工具。

本文采用有限元軟件ANSYS分析了《NB/T 47041—2014<塔式容器>標準釋義及算例》(以下簡稱“標準算例”)中例題1～例題4所示的4臺不同類型塔器的自振特性，并與NB/T 47041中的計算方法進行了比較，著重分析了不等截面塔器自振周期及振型函數。

1 ANSYS分析過程

ANSYS分析的過程主要包括：定義單元類型、截面特性、材料屬性，建立模型，賦予模型材料屬性和劃分網格，施加約束和載荷，求解，以及后處理。

采用ANSYS 15.0的2節點管單元pipe288劃分模型網格。ANSYS幫助文件的說明顯示，pipe288單元基于鐵木辛柯梁理論，考慮了梁的剪切變形，適用于細長、中等粗短的管結構。與實體單元、殼單元相比，管單元的建模、網格劃分都較為簡單，便于工程技術人員掌握和運用。

建模時，首先按塔器的幾何尺寸及分段數創建關鍵點，再由關鍵點生成直線即可。對于線模型的網絡劃分，只需指定單元長度或單元數。需要指出的是，集中質量法、矩陣迭代法的分段數與自由度個數對應【4】，ANSYS求解中的自由度個數與網格數目對應，而不是與模型中的分段數對應。另外，借助ANSYS參數化設計語言實現了仿真全過程的參數化，避免了繁瑣的界面操作，便于進行分析研究。

另外，ANSYS計算還應注意【3】：

1) 在定義單元屬性時，需要將單元行為方式定義為三次函數，以提高精度。

2) 在確定材料屬性的密度時，需要將操作質量m0折算成塔體等效密度ρe，即(公式中的符號解釋，除特殊注明外，均與文獻【2】一致，下同)：

式中：ρe——塔體等效密度，kg/m3；

V——塔器金屬殼體體積(計算時殼體厚度取名義厚度，與標準算例保持一致)，m3。

3) 對于沒有其他支撐的自支承式塔器，模型底部應施加全約束。而若只是求解自振特性，無需施加其他載荷。

4) 模態提取方法設為分塊蘭索斯法(Block Lanczos)，模態提取階次及擴展階次本文設為6階。

2 等截面塔器的計算

2.1 例題1

標準算例中的“例題1”為φ1 400 mm×18 900 mm等直徑泡罩塔，高徑比H/D=13.5<15，且H<20 m，根據NB/T 47041中7.5.4的規定，可以不考慮高振型。按NB/T 47041式(19)計算其基本自振周期T1：

頻率f1=1/T1=1.429 Hz。

ANSYS計算的主要參數為 ：截面特性中壁厚取殼體有效厚度0.005 m；設計溫度下材料的彈性模量Et為1.97×1011Pa，泊松比ν取0.3；等效密度ρe為56 701 kg/m3;V為圓筒的體積，(圓筒內徑為1.400 m，厚度0.005 m，高度18.900 m)；忽略封頭等零部件，與標準算例一致。由2個坐標分別為(0.0,0.0,0.0)、(0.0,18.9,0.0)的關鍵點創建直線，因為操作質量沿高度均勻分布，因此模型無需分段；網格數設為100。

式中：i——第i階的相對誤差；

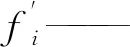
fi——按NB/T 47041中相應公式計算得到的第i階自振頻率，Hz。

2.2 例題3

標準算例中的“例題3”為φ2 400 mm×73 300 mm 的等直徑等厚度浮閥塔，高徑比H/D=30.4>15，且H>20 m，需考慮高振型。標準算例按NB/T 47041附錄B(即矩陣迭代法)計算其前3階自振周期，有T1=3.828 9 s，T2=0.610 9 s，T3=4.541 3 s，則頻率分別為f1=0.261 Hz，f2=1.637 Hz，f3=4.541 Hz。

圖1 例題1振型

ANSYS計算的主要參數為：壁厚取有效厚度0.019 m；Et=1.95×1011Pa，ν=0.3，ρe=22 168 kg/m3；由(0.0,0.0,0.0)、(0.0,73.3,0.0)2個關鍵點創建直線，模型不分段；網格數設為200。

ANSYS與NB/T 47041附錄B的計算結果非常接近，各階最大相對誤差不超過1.20%，見表1。

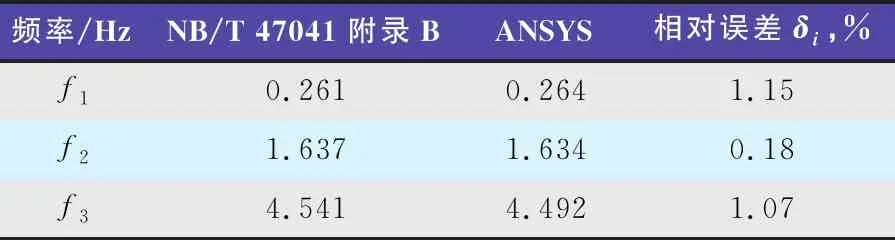
表1 例題3計算結果比較

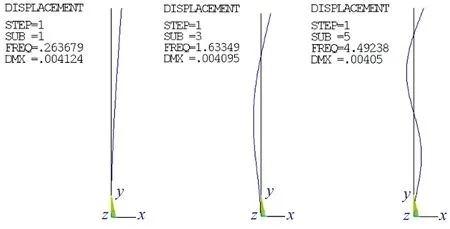
圖2 例題3振型

3 不等截面塔器的計算

3.1 例題2及其模型改進

標準算例中的“例題2”為φ800 mm/φ400 mm/φ800 mm×18 400 mm的不等直徑填料塔，高度方向上截面尺寸變化較大，塔高H<20 m，無需考慮高振型。標準算例按NB/T 47041的式(16)(即集中質量法)計算其自振周期T1=1.29 s，即f1=0.775 Hz。而本文采用ANSYS計算得到的基本自振頻率為1.147 Hz，兩者相對誤差達48%，誤差較大，需要進一步分析。

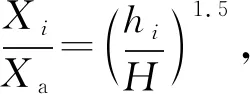
對于振型函數假定困難的塔器，還可采用矩陣迭代法計算自振周期。與集中質量法相比，矩陣迭代法的計算結果與主振型函數并不直接相關，準確度也較高【6】。但矩陣迭代法計算量大，手算困難，通常借助計算機程序進行。本文將例題2的塔器“加高”，φ400 mm部分由8 600 mm加長至10 400 mm，塔器總高為20 200 mm，其余尺寸不變，如此便可借助SW6軟件進行矩陣迭代法的計算【7】。

本小節采用改進的“例題2”塔器模型，比較了集中質量法、ANSYS有限元法、矩陣迭代法在自振周期計算中的運用。

3.1.1 NB/T 47041的集中質量法

運用集中質量法計算“改進后的例題2塔器模型”的自振周期，參數見表2。

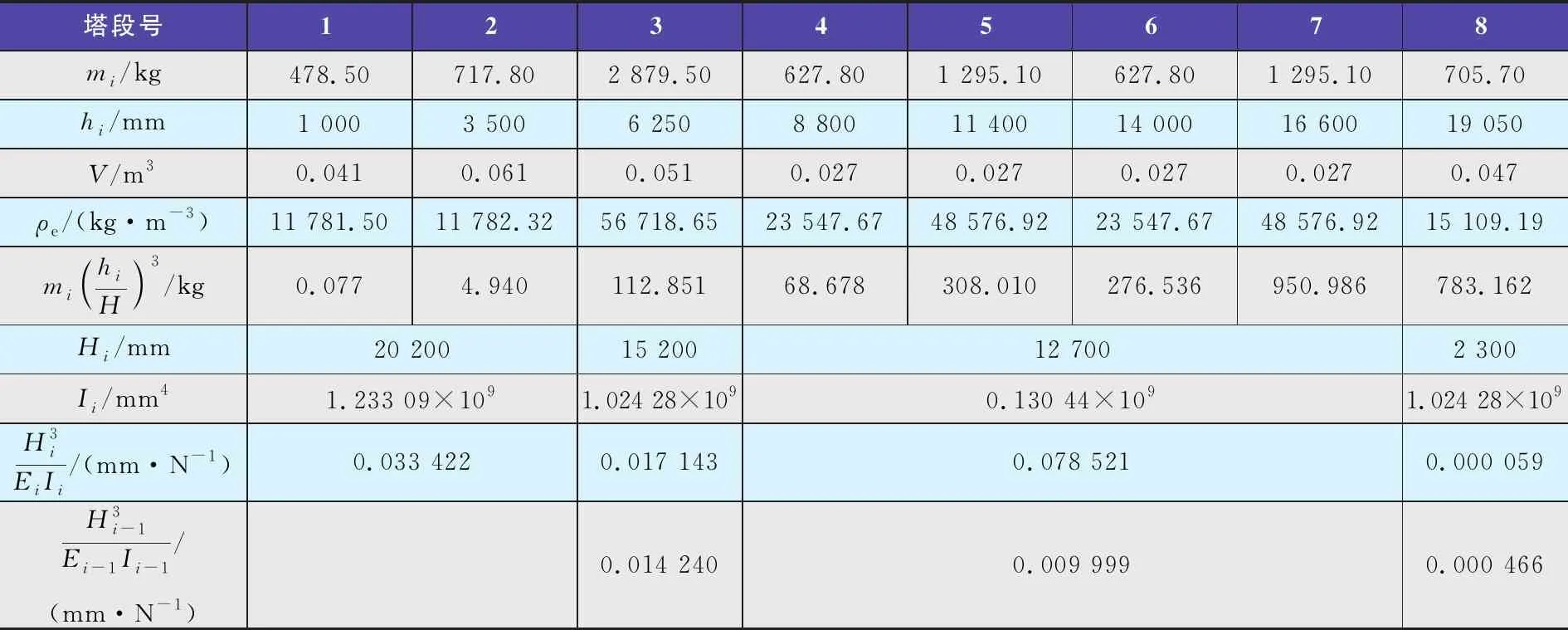
表2 改進的例題2塔器自振周期計算

由表2有：

則

0.035 mm/N即為頂端作用單位力的變截面梁的位移【1】。

按NB/T 47041的式(16)計算得到的基本自振周期為：

基本自振頻率為0.539 Hz。

3.1.2 ANSYS模態分析

ANSYS計算主要參數為：壁厚取各段有效厚度；Et=2×1011Pa，ν=0.3；創建9個關鍵點并生成8條直線，分段設置截面特性、等效密度ρ，見表2；網格長度設為0.01 m，節點共計2 021個，其中1號節點為坐標原點。

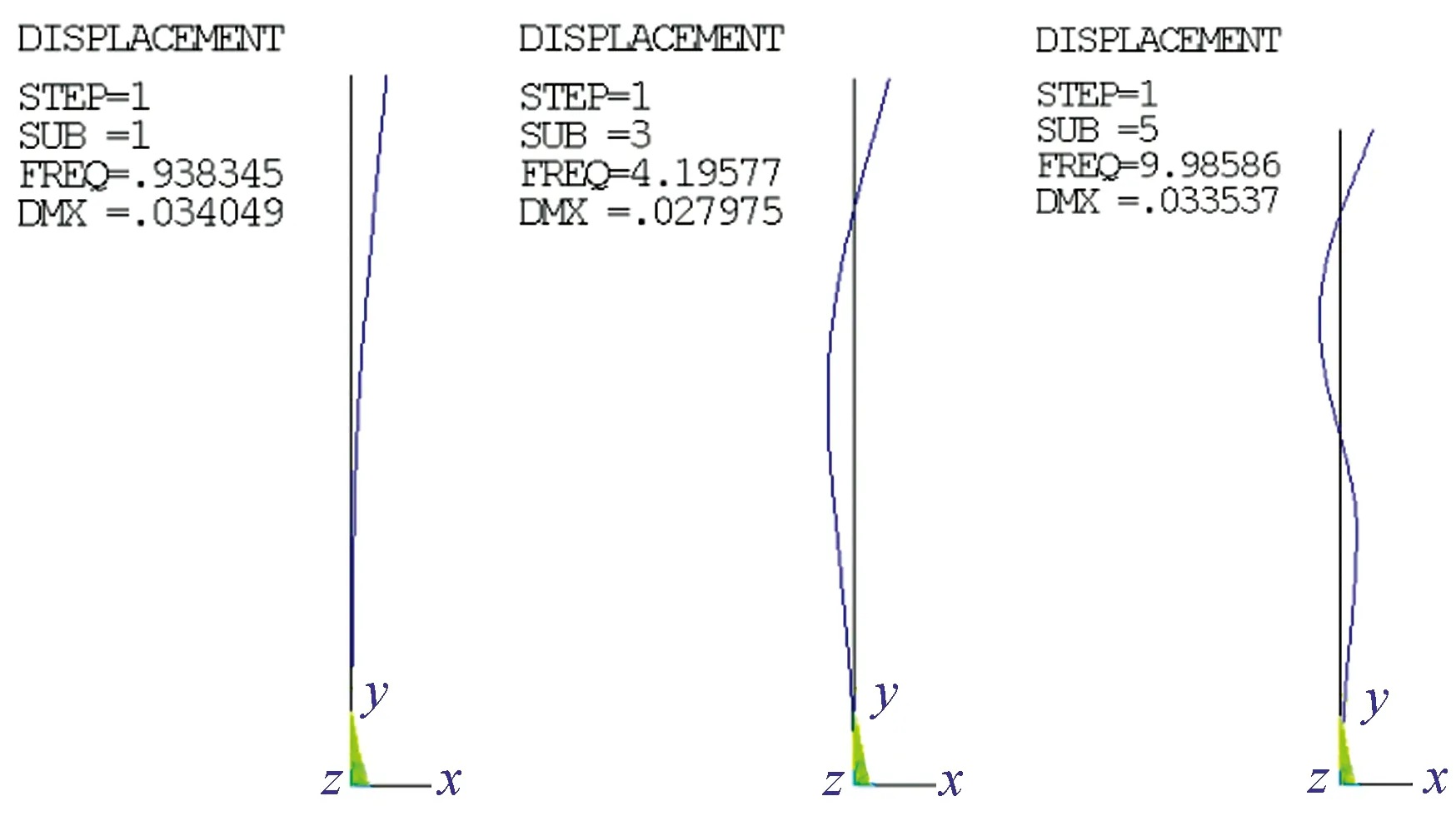
圖3 改進后的例題2的振型

3.1.3 由ANSYS提取振型函數的集中質量法

在ANSYS的后處理器中可提取各節點的位移，設塔器的一階振型函數為：

式中：Xi——節點i在x軸方向上的位移，mm；

Xa——最大位移，mm。

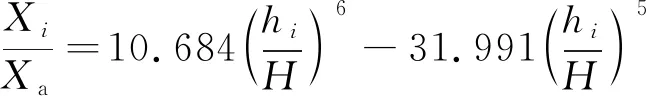
相關系數R2=1。

從圖4可以看出，ANSYS計算得到的振型函數，與NB/T 47041集中質量法所假設的振型函數相差較大。

圖4 振型函數

根據集中質量法的能量相等原理【1】，對于擬合得到的多項式振型函數，基本自振周期計算式為：

按表2的分段方法，進行新振型函數周期計算，其中間計算結果見表3。

表3 新振型函數計算周期的中間計算結果

3.1.4 結果比較與分析

另外，借助SW6軟件進行了矩陣迭代法的計算，各種方法的計算結果列于表4。

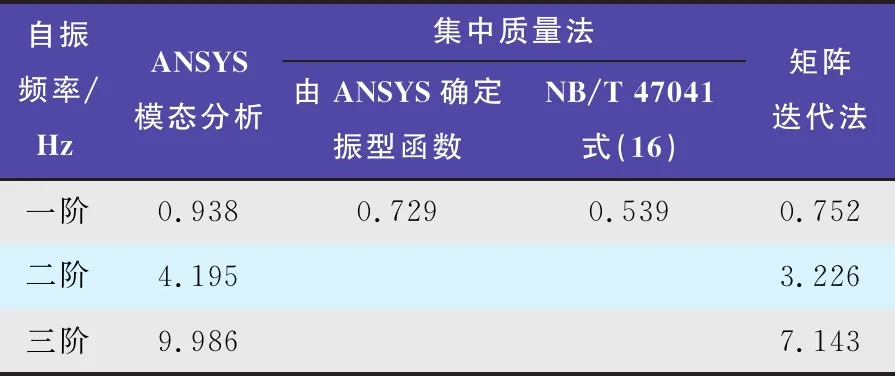
表4 各方法計算結果比較

對于一階自振頻率，由表4可以看出：

1) ANSYS模態分析結果，與采用ANSYS振型函數的集中質量法，有30%的誤差。

這是因為集中質量法中自由度個數與分段數對應，段數越多計算越準確【8】，這個數目要遠小于ANSYS的網格數(或自由度個數)。可以推斷，若增加分段數集中質量法的計算結果將與ANSYS 數值解趨近。

2) 而采用ANSYS振型函數的集中質量法，與矩陣迭代法計算結果誤差為3.1%，兩者較為接近，和ANSYS模態分析的誤差也在25%左右。與集中質量法類似，矩陣迭代法的精度同樣與分段數有關，SW6以1 m為一段【7】，而本小節ANSYS 計算中的單元長度為0.01 m。

3) NB/T 47041式(16)計算所得的自振頻率是幾種方法中最小的，即周期最大，這對于抗震設計等是偏于不安全的。原因在于，式(16)所采用的振型函數是不準確的。

3.2 例題4

標準算例中的“例題4”為φ1 400 mm/φ1 200 mm×48 000 mm的不等直徑等厚度浮閥塔，高徑比H/D>15，且H>20 m，需要考慮高振型。標準算例按NB/T 47041附錄B(矩陣迭代法)計算其前三階自振周期為T1=2.00 s，T2=0.42 s，T3=0.15 s，對應的頻率分別為f1=0.5 Hz，f2=2.38 Hz，f3=6.67 Hz。

標準算例將該塔器分為12段(見標準算例的表4-1)，但標高14 000～18 500 mm(即第4、5段)、標高31 000～39 000 mm(即第8、9、10段)的操作質量、截面特性一樣，可以分別合并成一段，本文ANSYS模型中將其分為9段。

ANSYS計算中主要參數為：壁厚取各段有效厚度；Et=1.94×1011Pa，ν=0.3；創建10個關鍵點并生成9條直線，分段設置截面特性、等效密度ρe；網格長度設為0.01 m。

ANSYS與NB/T47041附錄B的計算結果及其相對誤差見表5，前兩階誤差較小，第三階誤差為5.77%。

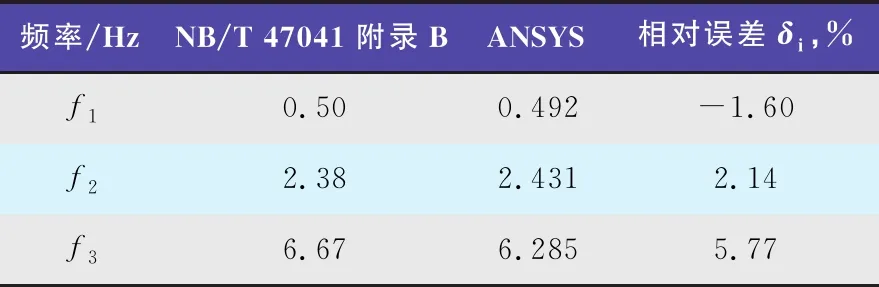
表5 例4計算結果比較

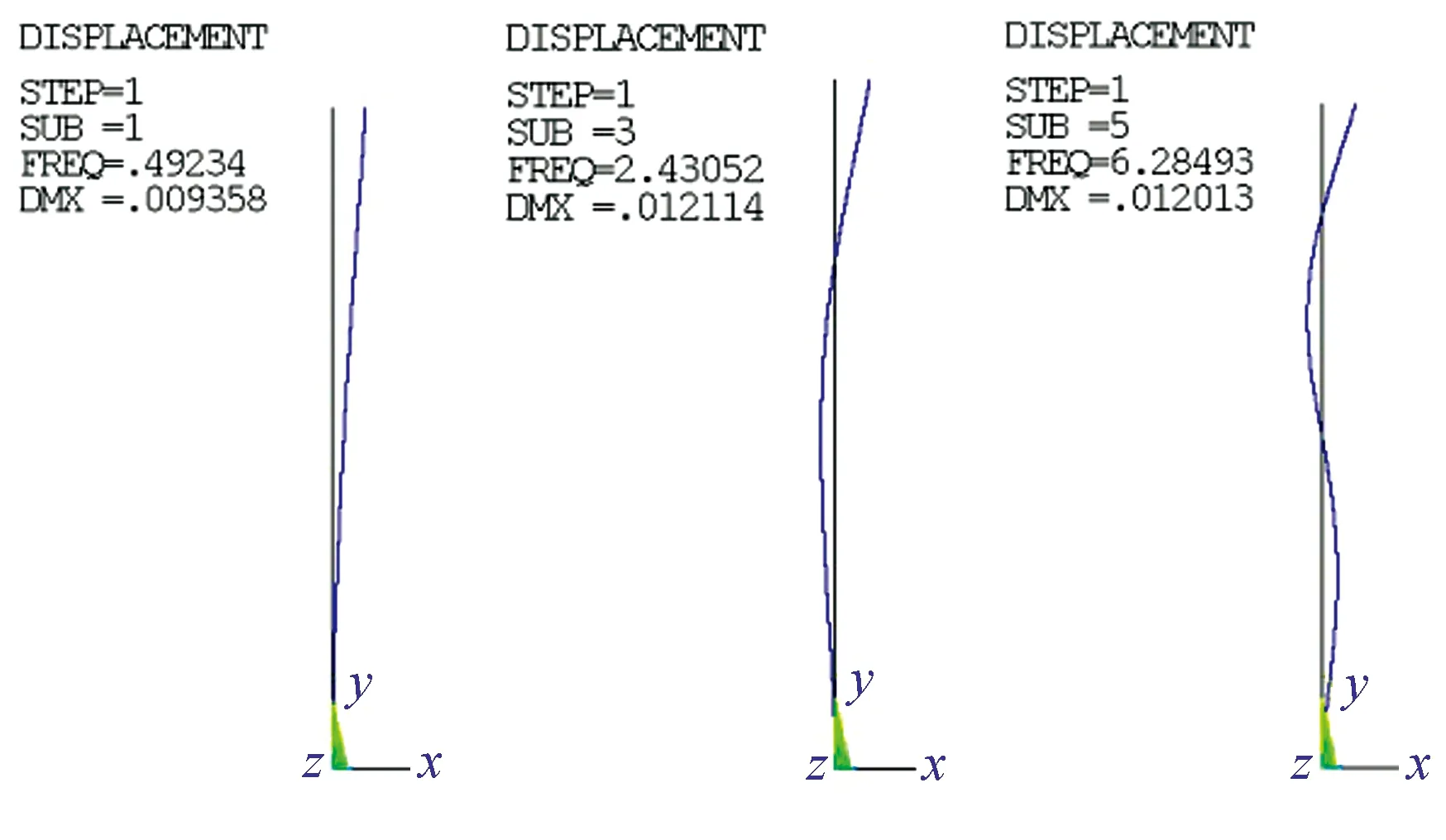
圖5 例題4振型

4 結語

對于《NB/T 47041—2014<塔式容器>標準釋義與算例》中例題1～例題4的4臺塔器自振周期(或頻率)對比計算有：

1) 對于等截面塔器(例題1、例題3)，ANSYS模態分析與彈性連續體解析法、矩陣迭代法的相對誤差較小，最小0.18%，最大不超過1.20%；

2) 對于截面變化不大的不等直徑塔器(例題4)，ANSYS與矩陣迭代法在前三階的相對誤差分別為-1.60%、2.14%和5.77%；

3) 對于截面變化較大的不等直徑塔器(例題2及其改進模型)，ANSYS與集中質量法、矩陣迭代的誤差均較大；

將例題2塔器“加高”至H>20 m， 以便借助SW6進行矩陣迭代法的計算， 并全面比較了ANSYS 模態分析、 集中質量法、 矩陣迭代法， 發現：

a) 提取ANSYS模型中各節點位移，整理后擬合得到新的振型函數，該振型函數與NB/T 47041假定的振型函數有較大差異；

b) 在集中質量法中運用“新的振型函數”后，計算得到的塔器自振周期，與矩陣迭代法計算得到的結果誤差較小(3%左右)；

c) 矩陣迭代法及采用了“新的振型函數”的集中質量法，與ANSYS模態分析均有較大誤差。

這3種方法都是將具有無限自由度的實際結構簡化為多自由度體系，對于截面變化較大的塔器，需要更多的自由度數目，可以認為，ANSYS的計算是更為準確的。

綜上所述，ANSYS模態分析對塔器自振周期的計算是準確的、可靠的，并且容易掌握。雖然有限元模態分析法未納入NB/T 47041塔式容器標準，但仍可作為塔器抗振設計的參考方法，尤其是對于變截面塔器。