一種使用分區邏輯合并的IMA分區分配方法
文/鄭磊
1 引言
分區向模塊的分配問題是IMA航電總體配置必須要涉及的問題,在分配過程中需要綜合考慮模塊調度和通信延遲等限制條件。若將分區看作是周期運行的任務,那么分區向模塊的分配就類似于多處理器任務分配問題。O.Kermia[2]與J.Korst[3]等人針對無占先限制的周期任務向多處理器分配的問題提出了快速啟發式算法;T.Davidovic[4]等人針對在多處理器上非周期任務調度問題引入了MILP公式;S.Thanikesavan[5][6][7]探討了基于MILP公式的的多處理器周期任務調度問題。針對IMA分區分配問題,P.Bieber[8][9]等人從安全性和可靠性需求角度研究了應用向模塊分配的問題;Ahmad[10]等人針對這一問題,通過將所有的約束條件線性化利用了MILP方法,在使用圖論進行一步初始化簡化變量數量后對該方程進行解析求解。由于問題本身變量數量的龐大,問題解算時間隨著分區數量和模塊數量的增多而增加,因此必須采用必要的簡化方法減少分區分配問題的解算時間,使用圖形理論進行問題簡化是非常有效的方法。
本文使用圖形理論對分區分配問題進行進一步簡化,提出分區合并算法達到減少算法解算時間的目的。
2 分區分配模型
以M表示Nm個IMA模塊的集合,即M={m1,m2,…,mNm,},P為Np個分區的集合,即M={p1,p2,…,pNp,}。設各個IMA模塊具有同一性,即任意分區pj∈P可以在任意模塊mk∈M上運行,分區的執行時間并不依賴于任一模塊。任意模塊mk∈M具有兩個基本屬性,分別為總可用存儲空間Rk和最大分區數Nk。由于模塊的同一性,設模塊間的通信延遲為一定值,則分區間的通信延遲主要由分區通信本身決定。分區間的通信延遲受模塊影響部分可用一延遲矩陣Δ來表示:

其中δi,j代表代表分區pi和pj分配到不同模塊后的通信延遲受模塊影響部分。
任一分區pj∈P具有如下屬性:
(1)ΕjP,分區pj的執行時間;
(2)TjP,分區pj的運行周期,顯然有ΕjP≤ TjP;
(3)rj,分區需求的存儲空間。
以tj(1)表示分區pj的第一次執行的開始時刻,那么由于分區運行的嚴格的周期性,它的第k次運行的開始時刻tj(k)則為:

出于某些安全性考慮,可能出現某兩個分區不可以分配到一個模塊中的情況。以 表示這樣的分區組(pi,pj)∈P2的集合,其中分區pi和pj不可以分配到同一模塊。
系統中的各個分區在運行時會進行各種形式的通信,在行為上表現為接收和發送數據。以Λ表示系統中所有NΛ個通信路徑向量的集合,即其中λir表示第i個通信路徑向量,它由該路徑所經過的所有r個分區序列組成,若通信路徑λir先后經過分區 pj,pk…pl,有 λir=(j,k,…,l)。 以 L(λir)表示 通信路徑λir端到端的通信延遲。
定義一個包含二進制變量ai,j的矩陣A來表示分區向模塊的分配。

在分區向模塊分配過程中一個正確的分區分配必須滿足如下三種限制條件:
(1)調度限制:分配到同一個模塊中的分區不能有執行時間上的重疊。
(2)資源限制:分配到同一個模塊的所有分區所需求的存儲空間之和要小于模塊的總可用存儲空間;分區數量之和要小于模塊可載有的最大分區數;一個分區只能被分配到一個模塊中;滿足(pi,pj)∈ε的兩個分區不能分配到同一模塊中。
(3)通信延遲限制:每一個通信路徑端到端的延遲L(λir)要小于最大可允許的延遲上限 Lmax(λir)。在給定分區集合向多模塊分配的問題中,就是要尋找一個方法使得該方法產生的結果能夠滿足上述所有的限制條件。
2.1 分區分配中的調度限制
由式(2)可得分區pj第k次運行的時間區間為Ik(tj(1) )=[tj(k),tj(k)+ΕjP]。限制條件:分配到同一個模塊中的任意兩個分區pi和pj不能有執行時間上的重疊就可以表述為

圖1:模塊間通信延遲
圖2:同一模塊內分區的調度延遲
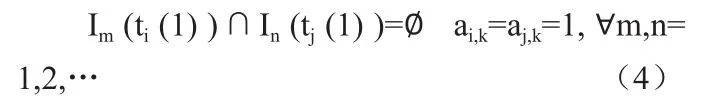
Korst在文獻[3]中提出的兩個周期任務執行時間不發生重疊的充分必要條件可以應用于分區調度范疇中:

其中,gi,j為分區周期TiP與TjP的最大公約數。
分區對處理器的總占用率Uim不能大于1,若模塊mi分區數為ni,有:
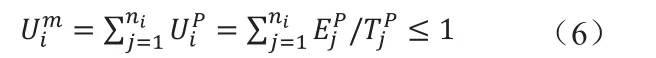
其中UiP=ΕjP/TjP為分區pj的處理器占用率。
2.2 分區分配中的資源限制
分配到同一個模塊的所有分區所需求的存儲空間之和Rjm要小于模塊的總可用存儲空間可表示為:
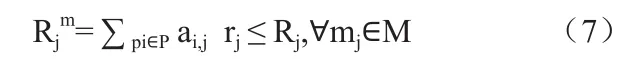
分配到同一模塊上的分區數量之和要小于模塊可載有的最大分區數可表示為:

一個分區只能被分配到一個模塊中可表示為:

滿足(pi,pj)∈ε的兩個分區不能分配到同一模塊中可表示為:

2.3 分區分配中的通信延遲限制
在分區分配過程中,對任意通信路徑λir∈Λ,端到端的延遲 L(λir)要小于最大可允許的延遲上限。端到端的通信延遲為整條通信鏈路中的分區的執行時間與分區間通信延遲之和,可用下式表示:
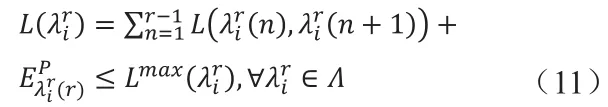
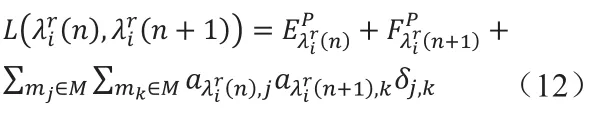
3 使用分區邏輯合并簡化模型
由式(5)可獲得在分區調度限制下不可分配在同一模塊上的分區組的集合,并使之與滿足 (pi,pj)∈ε的集合合并為集合 Ε,(pi,pj)∈Ε則為所有不可分配在同一模塊上的分區組的集合。
由式(11)和(12)可得任意通信路徑延遲的最大值為:
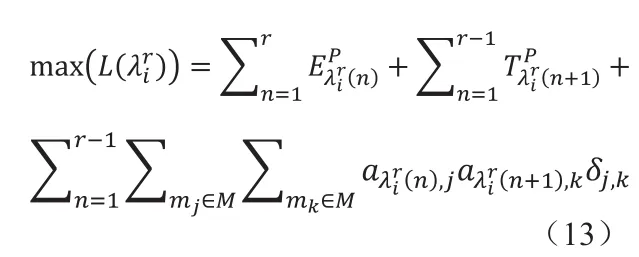
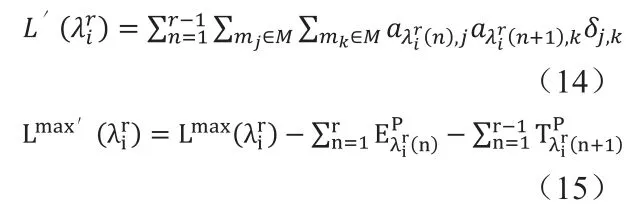
其中 L'(λir)和 Lmax'(λir)分別為只考慮分區分配造成的最大延遲和該延遲的上限值。若 L'(λir)>Lmax'(λir),則該通信路徑中至少有兩個分區必須分配到同一模塊上,對于通信路徑最多可以有r-1個這樣的分區組合。
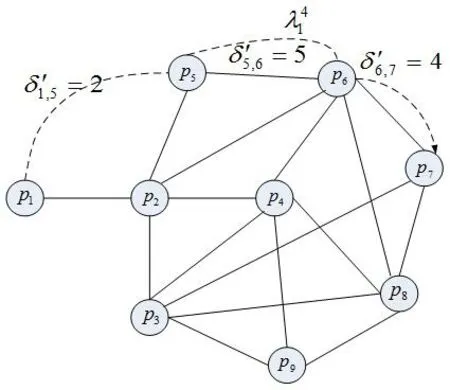
采用圖型理論進行模型簡化可以在極大限度上減少變量的數量。在分區分配問題中可采用如圖3所示分區關系圖G[10]:
在圖3中,每一個節點代表一個分區,兩個分區間的連線表明這兩個分區可以分配到同一個模塊上,反之沒有連線的兩個分區則不能分配到同一模塊上,即滿足(pi,pj)∈Ε。
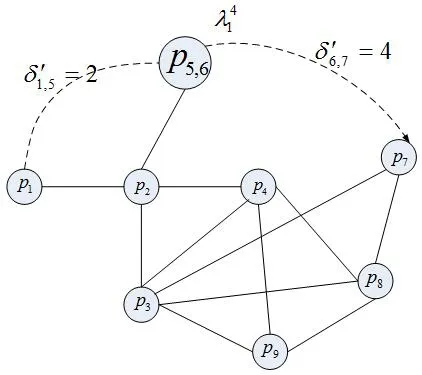
類似于最大無關組(MIS)[11]的概念,在該圖中可以找到這樣一個集合B,該集合包含的所有分區彼此互相不能分配到同一模塊上,如在該圖中有(p1,p3,p6)∈B。在分區路徑λir延遲 L'(λir)>Lmax'(λir)的約束下,可以找到r-1個必須分配到同一模塊的分區組合,并將pi,pj兩個分區合并成一個節點pi,j進行考慮,在合并的同時,新節點要繼承原先節點與其他節點互斥關系。設集合Dg為以pi,j為元素的集合,即pi,j∈Dg。在圖3中,虛線表示一條通信路徑λ14,它先后經過分區p1,p5,p6,p7,若有Lmax'則(p5,p6)或(p6,p7)必須分配在一個模塊中,將(p5,p6)節點合并后的關系圖Gg'為圖4,(p6,p7)的合并與之同理。
4 分區分配方法流程
整個分區分配算法包含如下幾步:
(1)由式(5)解算出所有滿足(pi,pj)∈Ε的分區組合,并作出分區間關系圖G。
(2)由式(15)和(16)對每一條通信路徑進行分析,求解出所有pi,j∈Dg,并在關系圖G中合并相關的pi和pj獲得關系圖Gg'。若總共有Nλ條通信路徑,則關系圖Gg'的最大數量NG為
(4)將Bg所包含的分區分配到每一個模塊中(一個模塊最多分配一個分區或合并后的分區對)。設必須分配到模塊mk中的分區組成的集合為若有pi∈Bg必分配到模塊mk中,則有
(6)對所有Nm個模塊作運算其 中 l=1,2,…,Nm,且l≠k獲得只能分配到模塊mk的分區,并將同時滿足式(6~8)條件的分區分配到模塊mk。
(7)重復5)和6),直到無法獲得只能分配到一個模塊中的分區。這樣就可以獲得對應于每個Gg'的兩種數據:其一為必須分配到各個模塊的分區集合其二為可分配到兩個以上模塊的分區集合和每個分區 pi∈Pg'可以分配的模塊的集合Mpig。集合Pg'所含分區只須滿足式(6~8)的限制條件就可以分配到各個模塊。
(8)在集合Mpig中,找出當前模塊處理器占用率最小的模塊mk,將集合Pg'中處理器占用率UjP最大的模塊分配到mk中,分配的同時要滿足式(7)和(8)的約束條件。
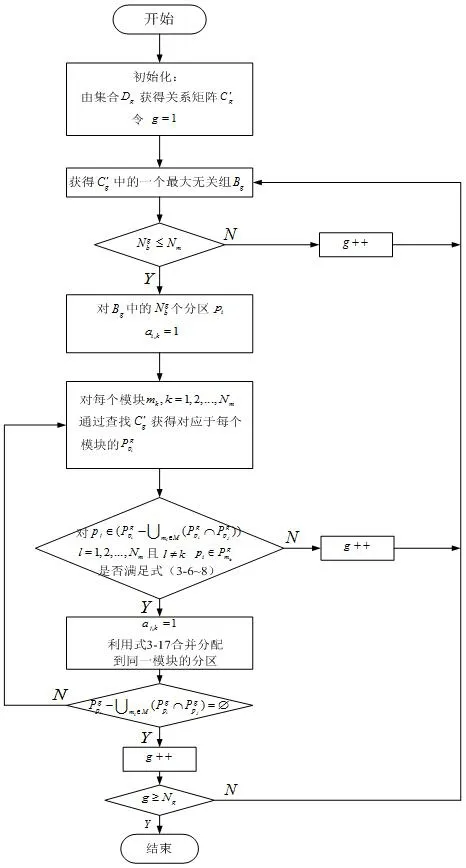
引入Np維矩陣C=[ci,j]表示分區之間的關系,若分區pi,pj可以分配到同一模塊上,則ci,j=1,反之 ci,j=0,ci,j=cj,i,若 i=j規定 ci,j=0。分區間的合并可以通過矩陣元素間的邏輯運算來表示,算法如下:若分區pj和pk(j 若分區關系如圖3,分區合并情況如圖4則有 該算法的流程如圖5。 由此,即可獲得對應于每個Gg'的和。 從算法解算過程可以看出,整個解算過程所需的邏輯運算次數較少,通過引入矩陣元素間的邏輯運算,使算法便于編程實現,并通過引入分區合并機制減少了運算次數,是一個可行的分區分配問題解決方案。 圖3:分區關系圖 圖4:合并后的分區關系圖 圖5:分區分配算法流程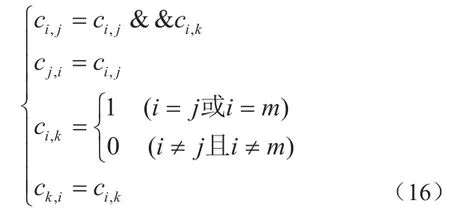

5 結語