貯箱輕量化設計幾何參數優化方法
辛騰達,王華,崔村燕,趙繼廣,韓向陽
(1.航天工程大學研究生院,101416,北京;2.航天工程大學宇航科學與技術系,101416,北京;3.航天工程大學電子與光學工程系,101416,北京)
推進劑貯箱不僅用來貯存約占液體火箭起飛質量90%的推進劑,而且是火箭重要的承力構件[1]。貯箱的輕量化設計可以有效提高火箭的有效載荷運載能力,是發展重型火箭的關鍵技術之一,每減少1 kg火箭質量可節省約2萬美元的發射成本[2]。目前,貯箱的輕量化設計主要體現在進行關于貯箱材料、制造技術及貯箱結構三方面的研究。
貯箱材料與制造工藝的發展,可為貯箱設計帶來巨大變革,具體應用包括:美國航天飛機使用了2195鋁合金,輕質外貯箱質量減少了3 405 kg[3-4];DC-XA火箭液氧貯箱使用了1460鋁鋰合金,質量減少了10%[5];NASA于2014年進行了輕質復合材料貯箱試驗,貯箱質量減少了30%,成本降低了25%[6];獵鷹9號火箭貯箱使用了新型2198鋁鋰合金,貯箱壁板采用了攪拌摩擦焊技術,成本僅為傳統結構的1/5[7-8]。
然而,貯箱材料與制造技術的發展通常需要高額的人力、物力及時間成本,因此貯箱結構的優化也成為貯箱優化設計的一種有效方法。國內外學者根據不同的設計需求,對貯箱結構進行了廣泛的研究,為推進劑貯箱的輕量化設計提供了重要參考。Szelinski等提出了sandwich貯箱壁設計方法,可有效改進低溫貯箱的熱力學性能[9]。Tapeinos等提出了multi-cell結構貯箱設計理念,并對貯箱在內壓及熱負荷作用下的性能進行了分析[10]。Fahmy等根據貯箱在諧波沉降作用下的性能,對貯箱壁厚參數進行了優化[11]。梁輝等應用零階優化的方法,對推進劑貯箱壁厚參數進行了優化設計[12]。Zhao等為改善加筋圓柱殼的局部屈曲現象,基于多島遺傳算法提出了一種分層網格結構的設計方法[13]。毛佳等人基于有限元分析的方法,對加筋圓柱殼結構參數進行了優化設計[14]。卜凡通過分析罐體的基本變形形式與應力分布特點,從強度、穩定性及抗震性能三方面對儲罐結構進行了優化[15]。Ansary等應用有限元分析的方法對加筋圓錐罐的壁厚、幾何形狀及加筋的尺寸與數量進行了優化設計[16]。郝鵬提出了一種基于等效剛度和精細模型的混合優化方法,為新一代火箭薄壁結構的設計提供了參考[17]。優化算法及有限元分析是結構優化設計的重要方法,但優化算法通常形式復雜,而有限元分析對模型參數依賴性高,需要精細的幾何模型作基礎,不利于工程實際應用。
目前,貯箱幾何參數的確定主要仍是根據工程手冊及工程師的經驗,并輔以有限元分析和地面測試。本文在分析橢球底圓柱貯箱應力分布的基礎上,以推進劑體積與貯箱所受應力為約束條件,以貯箱質量最小為優化目標,對推進劑貯箱幾何參數進行了優化,可為貯箱的工程設計提供一定的參考。
1 推進劑貯箱應力分析
1.1 橢球底圓柱貯箱模型
目前,承力式橢球底圓柱貯箱是液體火箭應用的主要貯箱類型,主要承受液體壓力、內部增壓、軸向壓力及推進劑重力[18]。根據推進劑貯箱的受力情況,建立承力式橢球底圓柱貯箱模型,如圖1所示。
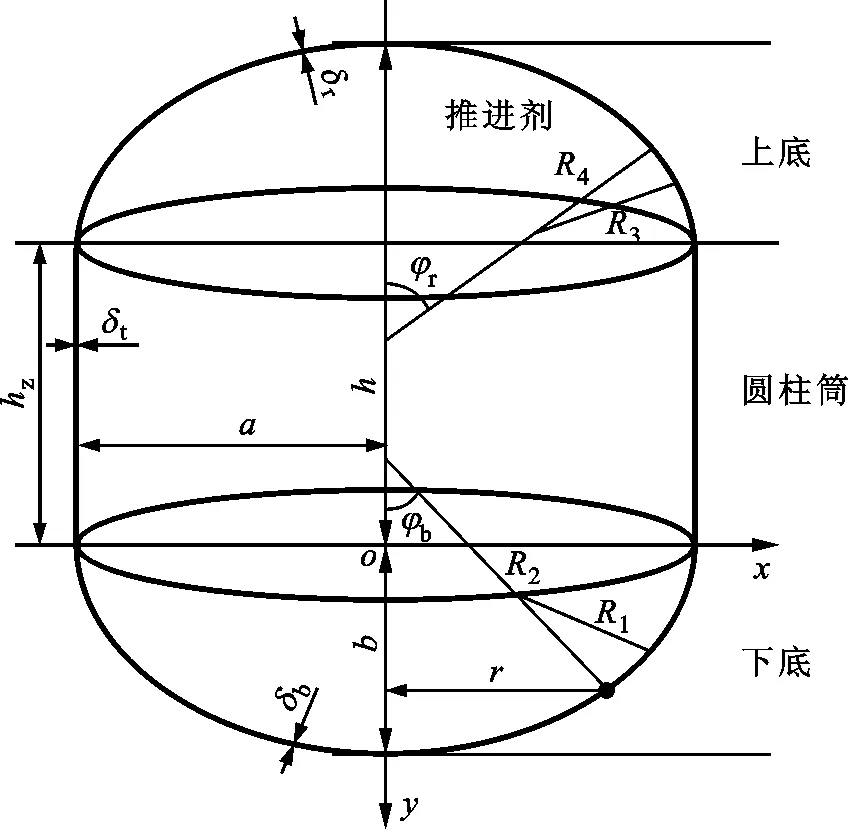
圖1 推進劑貯箱模型
圖1中:xoy為貯箱基準坐標系;δb為貯箱橢球下底壁厚;r為參考點到y軸距離;b為貯箱橢球底高度;R1和R2分別為貯箱橢球下底第一曲率半徑和第二曲率半徑;φb為貯箱橢球下底第二曲率半徑與y軸的夾角;R為貯箱半徑;δt為貯箱圓柱筒壁厚;hz為貯箱圓柱筒高度;h為推進劑液面高度,h=hz+b;δr為貯箱橢球上底壁厚;R3和R4分別為貯箱橢球上底第一曲率半徑和第二曲率半徑;φr為貯箱橢球上底第二曲率半徑與y軸的夾角。根據幾何關系,可知R1、R2和sinφb的數學表達式為
(1)
(2)
(3)
1.2 貯箱橢球下底應力分析
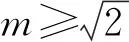
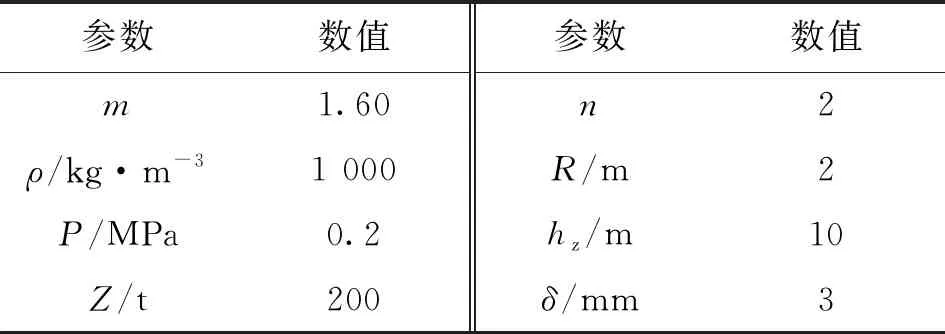
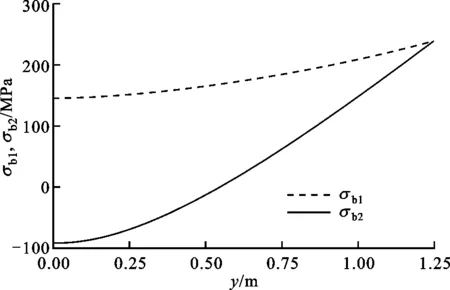
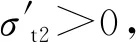
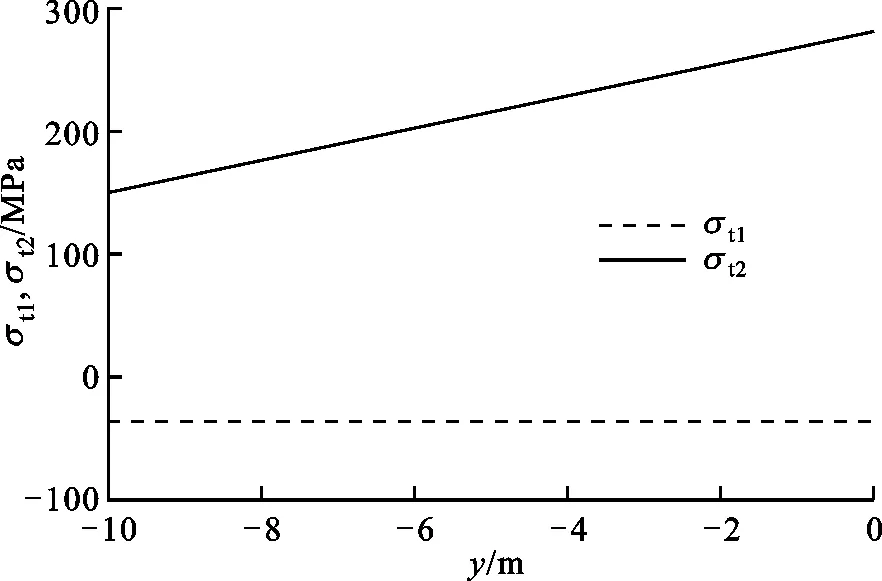
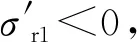
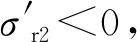
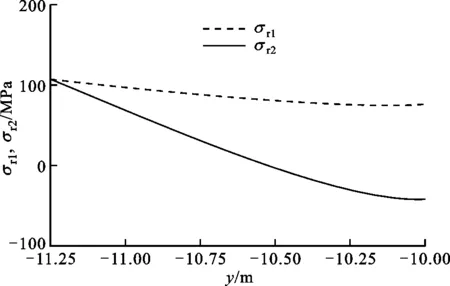
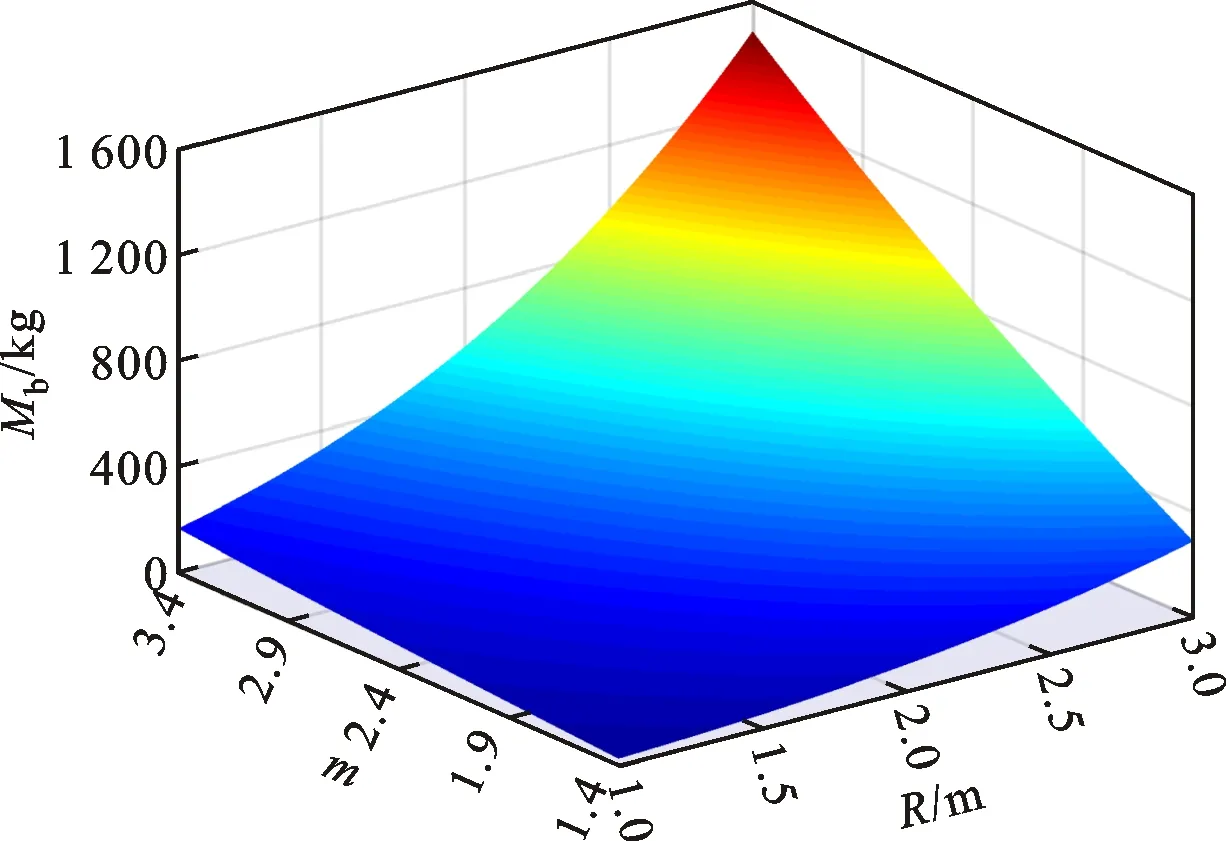
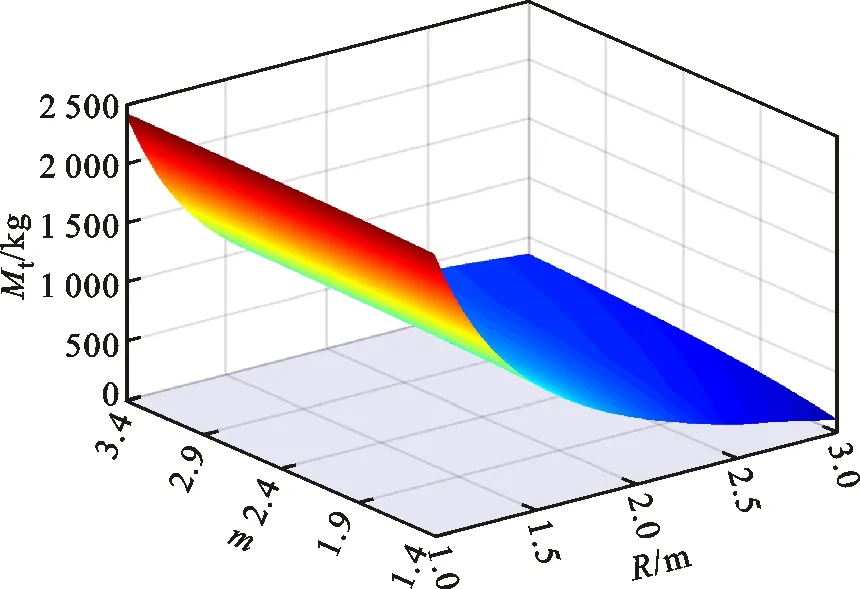
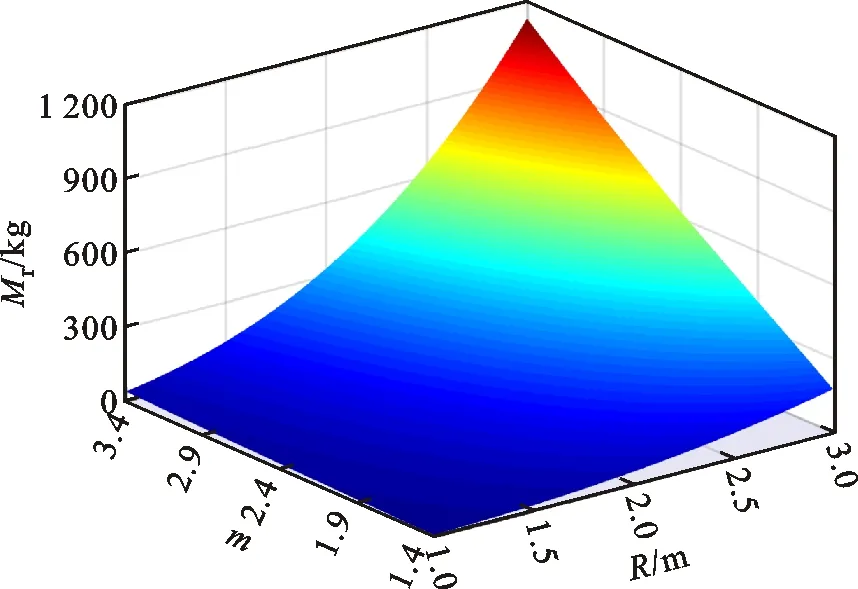
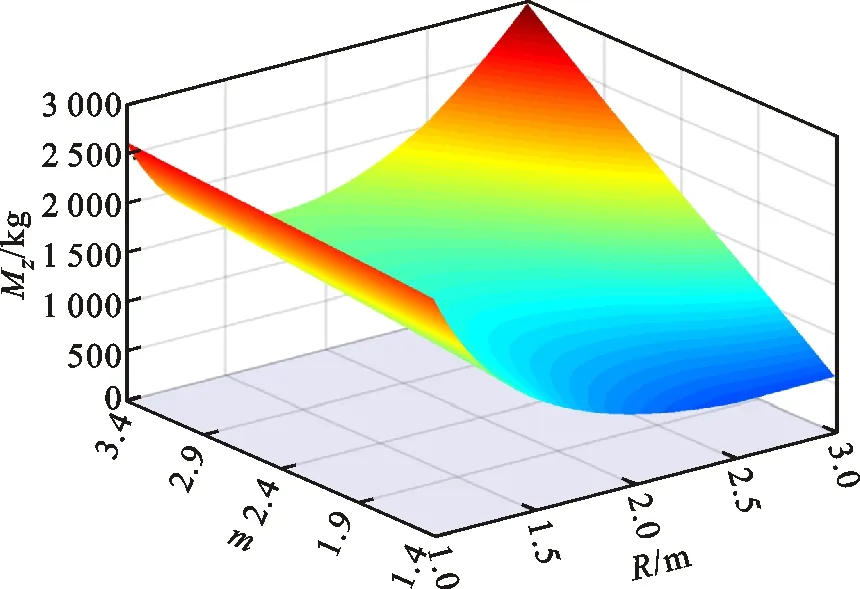
根據圖1可知,貯箱橢球下底(0 x2/R2+y2/b2=1, 0 (4) 若將橢球模數m定義為橢圓長半軸R(即貯箱半徑)與短半軸b之比,則可知m=R/b>1,結合式(1)~(4),可得 (5) 貯箱橢球下底任意橫截面上的力學平衡方程為 (P+gnρhb)πr2+gnρVb=σb12πrδbsinφb (6) 式中:P為貯箱內部增壓;σb1為貯箱橢球下底的經向應力;n為軸向過載系數;g為重力加速度,g=9.8 m/s2;ρ為推進劑密度;hb為推進劑液面到貯箱橢球下底任意橫截面高度,hb=h+y;π取為3.14;Vb為橢球下底任意橫截面以下部分的容積,公式為 Vb=2πR2b(1-1.5yb-1+0.5y3b-3)/3 (7) 據式(6)可得σb1的數學公式為 σb1=[(P+gnρhb)πr2+gnρVb]/2πrδbsinφb (8) maxσb1=mR(P+gnρh+gnρb)/2δb (9) 根據無矩理論,貯箱橢球下底任意單元的平衡方程為 σb1/R1+σb2/R2=(P+gnρhb)/δb (10) 式中σb2為貯箱橢球下底的環向應力。 結合式(8)和式(10),可得σb2為 σb2=(P+gnρhb)R2/δb-σb1R2/R1 (11) (12) 給定推進劑貯箱的幾何參數,如表1所示,即可得到貯箱各部分的應力分布。 表1 貯箱幾何參數示例 注:Z為火箭起飛質量;δ為貯箱壁厚參數。 若取δb=δ,則根據式(8)和式(10)可得σb1和σb2的分布,如圖2所示。 圖2 貯箱橢球下底的應力分布 分析圖2可知:貯箱橢球下底的經向應力σb1與環向應力σb2均隨貯箱縱坐標y的增加而增加;環向應力σb1始終表現為拉應力;因m=1.60,環向應力σb2存在壓應力向拉應力轉換的現象。 (13) (14) 結合式(13)和式(14),可得貯箱圓柱筒的經向應力σt1的數學公式為 σt1=PR/2δt-Zng/2πRδt (15) 根據式(15)可知,貯箱圓柱筒的經向應力σt1與y無關,且存在δt>0,因此σt1的正負取決于 f=PR/2-Zng/2πR (16) 由式(16)可知:當f>0時,σt1表現為拉應力;當f<0時,σt1表現為壓應力;當f=0時,σt1為0。 在內部增壓P及推進劑液壓Py作用下,貯箱圓柱筒的環向應力σt2的數學公式為 σt2=(P+Py)R/δt (17) 式中:P為內部增壓;Py為推進劑液壓,Py=gnρht,ht為推進劑液面到貯箱圓柱筒任意橫截面高度,ht=h+y。 maxσt2=(P+gnρh)R/δt (18) 若取δt=δ,根據式(15)、式(17)及表1可得σt1和σt2的分布,如圖3所示。 圖3 貯箱圓柱筒的應力分布 分析圖3可知:因f<0,貯箱圓柱筒的經向應力σt1表現為與貯箱縱坐標y無關的壓應力;環向應力σt2表現為隨貯箱縱坐標y的增加而遞增的拉應力。 貯箱橢球上底(即-h≤y<-hz部分)與橢球下底結構相同,即R3=R1、R4=R2、sinφr=sinφb。 貯箱橢球上底母線的橢圓方程為 x2/R2+(y+hz)2/b2=1 (19) 聯立式(1)~(3)及式(19)可得 (20) 貯箱橢球上底任意橫截面上的力學平衡方程可表示為 2πxσr1δrsinφr=πx2(P+ρnghr) (21) 式中hr為推進劑液面到貯箱橢球上底任意橫截面高度,hr=y+h。 將x=r=R4sinφr代入式(21),可得貯箱橢球上底的經向應力σr1為 (22) maxσr1=RmP/2δr (23) 貯箱橢球上底任意橫截面的力學平衡方程為 σr1/R3+σr2/R4=(P+gnρhr)/δr (24) 聯立式(22)和式(24),可得貯箱橢球上底的環向應力σr2的數學公式為 σr2=[(P+ρnghr)R4](2-R4/R3)/2δr (25) 根據式(25)可知:當(2-R4/R3)>0時,σr2表現為拉應力;當(2-R4/R3)<0時,σr2表現為壓應力;當(2-R4/R3)=0時,σr2為0。 minσr2=(mPR+ρngR2)(2-m2)/2mδr (26) 聯立式(22)和式(25)可得 σr1-σr2=PR4(R4/R3-1)/2δr (27) 由于P>0、R4/R3≥1,根據式(27)可知σr1≥σr2,當y=-h時,存在σr1=σr2,即maxσr1=maxσr2。 若取δr=δ,根據式(22)、式(25)及表1可得貯箱橢球上底的經向應力σr1與環向應力σr2的分布,如圖4所示。 圖4 貯箱橢球上底的應力分布 分析圖4可知:貯箱橢球上底的經向應力σr1與環向應力σr2均隨貯箱縱坐標y的增加而增加;經向應力σr1>0始終表現為拉應力;因m=1.60,環向應力σr2存在拉應力向壓應力轉換的現象。 通過對貯箱橢球下底、圓柱筒及橢球上底的經向應力與環向應力的分析,可知貯箱的應力分布可能存在拉應力與壓應力轉換的現象。本文根據材料強度理論對貯箱應力進行合理等效,并以此為依據確定推進劑貯箱設計所需的壁厚參數。 根據材料強度理論,貯箱的等效應力σe可表示[19]為 (28) 式中:σ1表示經向應力;σ2表示環向應力。 由式(28)可知,貯箱環向應力或經向應力的轉換現象將造成貯箱等效應力的突變,在貯箱設計中需要予以考慮。因此,為保證貯箱應力強度的可靠性,本文結合貯箱經向應力與環向應力的分布特征及式(28),將貯箱橢球下底、橢球上底的最大等效應力σeb、σer和貯箱圓柱筒的最大等效應力σet定義為 (29) 據式(28)和式(29)可知,始終存在σeb≥σe、σet≥σe及σer≥σe,為保證貯箱等效應力不大于貯箱材料極限應力,將σeb、σet及σer均取為貯箱材料的極限應力σs=290 MPa。因此,貯箱橢球下底、圓柱筒及橢球上底壁厚參數可以用數學公式表示為 (30) (31) (32) 以推進劑貯箱質量最小化為優化目標,對推進劑貯箱幾何參數進行優化設計。根據推進劑貯箱設計需求,所需推進劑體積V為已知量,貯箱圓柱筒高度hz的數學公式為 hz=V/πR2-4R/3m (33) 由式(33)可知,當m≤4πR3/3V時,hz≤0,即貯箱不存在圓柱筒段,因此在幾何參數的設計中需保證m>4πR3/3V。同時,隨著橢球模數m的減小,貯箱橢球上底與橢球下底逐漸變為半球形,不利于箭體空間的有效利用,在貯箱的實際設計中通常取m≥1.40。 根據式(30)~(33)可知,在給定貯箱設計需求參數的情況下(P、Z、ρ、n參照表1,V取為100 m3),貯箱橢球下底、圓柱筒及橢球上底質量完全可由貯箱半徑R及橢球模數m進行約束。 根據式(30)可得貯箱橢球下底質量Mb為 (34) 式中ρc為貯箱材料密度,取為2 640 kg/m3。 因此,可得貯箱橢球下底質量Mb隨貯箱半徑R與橢球模數m的變化,如圖5所示。 圖5 貯箱橢球下底質量的變化 分析圖5可知:貯箱橢球下底質量隨貯箱半徑與橢球模數的增加而增加;當貯箱半徑與橢球模數均取較小值時,橢球下底質量較小。 根據式(31)可得貯箱圓柱筒質量Mt為 (35) 因此,可得貯箱圓柱筒質量Mt隨貯箱半徑R與橢球模數m的變化,如圖6所示。 圖6 貯箱圓柱筒質量的變化 分析圖6可知:貯箱圓柱筒質量隨貯箱半徑的增加而減小;橢球模數對貯箱圓柱筒質量的影響較小;當貯箱半徑取較大值而橢球模數取較小值時,貯箱圓柱筒質量較小。 根據式(32)可得貯箱橢球上底質量Mr為 (36) 因此,可得貯箱橢球上底質量Mr隨貯箱半徑R與橢球模數m的變化,如圖7所示。 圖7 貯箱橢球上底質量的變化 分析圖7可知:貯箱橢球上底質量隨貯箱半徑與橢球模數的增加而增加;當貯箱半徑與橢球模數均取較小值時,橢球上底質量較小。 綜上所述,可得貯箱質量Mz為 Mz=Mb+Mt+Mr (37) 因此,可得貯箱質量Mz隨貯箱半徑R與橢球模數m的變化,如圖8所示。 圖8 表1所示火箭貯箱質量的變化 分析圖8可知:當貯箱半徑取小值時,貯箱質量較大,即細長型貯箱設計不可取;當貯箱半徑取大值、橢球模數也取大值時,貯箱質量較大,即粗平底型貯箱設計亦不可取;當貯箱半徑取大值,而橢球模數取小值時,貯箱質量較小。 從本節分析可知,根據推進劑貯箱設計參數,并且結合式(35)~(37),即可在保證貯箱應力強度可靠性的條件下,對貯箱半徑及橢球模數進行優化,為貯箱的輕量化工程設計提供參考。 以某型火箭貯箱設計參數為例,對提出的推進劑貯箱幾何參數優化方法進行驗證分析,該型火箭貯箱設計參數如表2所示。 將貯箱最大等效應力取為貯箱材料極限應力σs=290 MPa,即可得該型火箭貯箱質量Mz隨貯箱半徑R與橢球模數m的變化,如圖9所示。 表2 某型火箭貯箱設計參數 圖9 某型火箭貯箱的質量變化 分析圖9可知,當貯箱半徑取大值,而橢球模數取小值時,貯箱質量較小,火箭貯箱半徑與橢球模數的設計未處于最優狀態。這在一定程度上與火箭整體的氣動布局、總體空間利用及有效載荷的幾何參數有關,但結合貯箱的實際需求,僅對貯箱半徑或橢球模數做微小改進時,即可有效減小貯箱的質量,如表3所示。 表3 某型火箭貯箱質量對比 注:表中所示質量不包括貯箱加強結構及設備的質量。 分析表3可知:在1≤R/m≤3、1.5≤m≤3.5的范圍內,當R=2.62 m、m=1.50時,貯箱質量Mz取得最小值,此時相對于貯箱原始質量減小335.0 kg。在實際應用中,貯箱半徑的增大會嚴重影響火箭整體的氣動布局,而橢球模數的減小會直接影響箭體空間的有效利用,因此貯箱半徑R與橢球模數m難以取到最優值。然而,當貯箱半徑R不變,橢球模數m減小為1.58、1.56與1.54時,貯箱質量仍可分別減小5.7、11.5與17.3 kg;當橢球模數m不變,貯箱半徑增加為1.69 m、1.71 m與1.73 m時,貯箱質量亦可分別減小15.2、29.7與43.6 kg。表3結果表明:結合推進劑貯箱設計需求,對貯箱半徑R與橢球模數m進行優化設計可有效減輕貯箱質量,提高液體火箭有效載荷運載能力。 (2)貯箱圓柱筒的經向應力隨貯箱縱坐標y的變化而變化,可能為壓應力也可能為拉應力,而環向應力始終表現為隨y遞增的拉應力。 (3)結合推進劑貯箱實際設計需求,對貯箱半徑R及橢球模數m進行優化設計,可有效減輕貯箱質量,提高液體火箭有效載荷運載能力。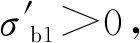
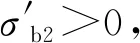
1.3 貯箱圓柱筒應力分析
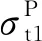
1.4 貯箱橢球上底應力分析
2 貯箱幾何參數優化方法
2.1 貯箱壁厚確定
2.2 貯箱幾何參數優化設計
3 驗證分析
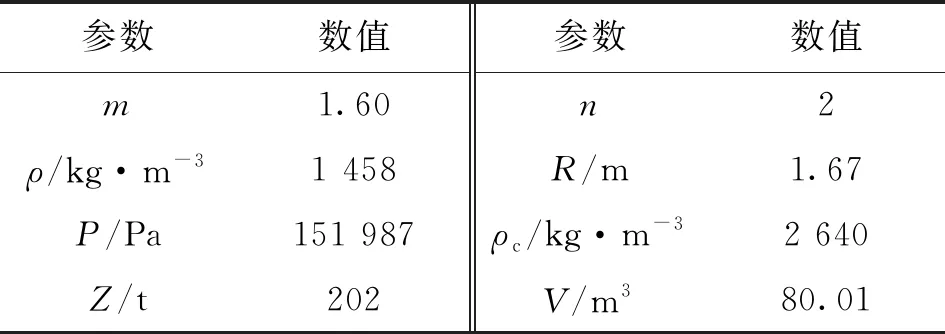
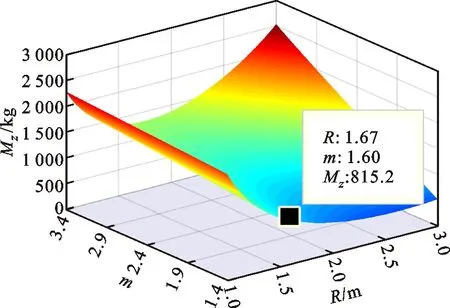
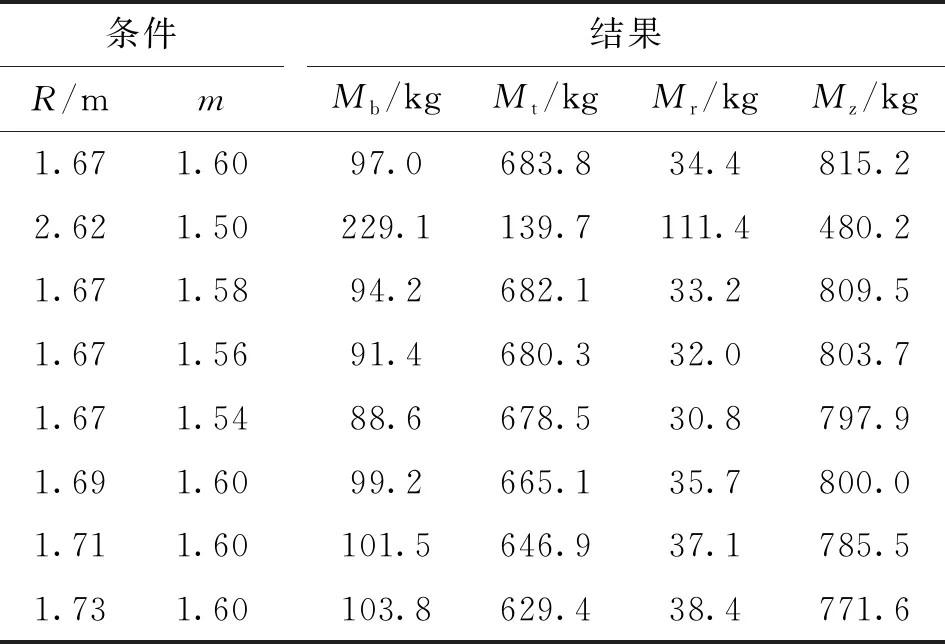
4 結 論

