采用增廣乘子法和模擬退火法的結構可靠性分析

高翔,王林軍,杜義賢

(1.三峽大學水電機械設備設計與維護湖北省重點實驗室,443002,湖北宜昌;2.三峽大學機械與動力學院,443002,湖北宜昌)

在工程實際中,由于受材料屬性、制造精度、安裝誤差等各種不確定因素的影響,結構的實際參數會偏離設計參數。為了在設計階段有效度量及控制不確定因素對結構的影響,需要通過可靠性分析來預先評估結構的失效風險。

關于結構的可靠性分析,國內外很多學者都進行了積極地探索和研究。Dempster和Shafer提出了證據理論,并且廣泛應用于非概率結構可靠性分析及可靠性優化設計[1-2]。Zadeh等對基于元模型的多目標多學科優化結構設計進行了研究,提出了求解多學科優化設計(multi-disciplinary design optimization,MDO)問題的EMOPSO法,該方法類似于MOPSO法,引入了SQP法和元模型,從而做出了位于Pareto解處的模糊邏輯決策[3]。Wang等對基于非概率集合理論的多學科可靠性優化設計問題進行了研究,提出了一種基于MDO策略的單循環算法,并且指出MDO策略主要包括MDF法、CSSO法、CO法、BLISS法[4]。Hao等對求解非概率可靠性優化設計問題的混沌控制方法進行了研究,提出了一種初期使用HL-RF法、振蕩時使用ECC法進行迭代的方法,并使用混沌動力學理論加速可靠指標的收斂速度[5]。為了提高ECC法的收斂性,在內層嵌套了Wolfe-Powell準則,用來檢查以及更新控制因子[5]。Hao等對桁架結構的可靠性優化設計進行了研究,提出了一種高效的IGA法,并且通過ESLA法和SSORASORM法提高了IGA法的計算效率[6]。Moon等對實驗數據不足情況下的基于信度的可靠性優化設計進行了研究,通過貝葉斯模型的核密度估計法計算概率密度函數,并由基于馬爾可夫鏈蒙特卡羅取樣器的MH算法計算后驗分布,最終利用Diracδ測度計算失效概率;由于Hellinger相似性的靈敏度不能用有限差分法計算,所以引入了復變量法;此外,指出DKG法是最準確的代理模型方法之一[7]。杜秀云等對基于Bregman距離函數的可靠性分析進行了研究,引入Bregman距離函數來計算可靠指標β,根據不動點同倫映射的思想構造同倫方程組進行計算,對極限狀態函數為非線性方程的可靠指標計算取得了良好的效果,尤其是極限狀態函數為指數函數的情況[8]。吉猛等對基于同倫分析的結構可靠性功能度量法進行了研究,使用KKT條件構造同倫方程組,并采用β-cone搜索方法追蹤到最可能點(most probable point,MPP),且使用優于可靠指標法的功能度量法來分析可靠性[9]。李彬等研究了基于改進自適應混沌控制的逆可靠性分析方法,運用自適應混沌控制方法進行了逆可靠性分析[10]。黃曉旭等對基于主動學習Kriging模型和子集模擬的可靠性分析進行了研究,提出了AK-SS法,對具有隱式功能函數的小失效概率計算取得了良好的效果[11]。孟增等對基于修正混沌控制的一次二階矩(first order second moment,FOSM)法進行了研究,運用混沌理論對迭代震蕩的情況進行修正,解決了極限狀態函數非線性程度較高時的迭代振蕩問題[12]。

盡管FOSM法在結構可靠性分析方面的理論已經很成熟,然而在實際工程的結構可靠性分析中卻很少使用,原因如下:①如果功能函數比較復雜,將會導致雅可比矩陣的計算變得煩瑣,從而整個過程效率低下;②如果雅可比矩陣的條件數過大,將會導致結果誤差較大;③通過極限狀態方程求解雅可比矩陣的過程中涉及到單位換算,極易得到錯誤的雅可比矩陣,這將導致可靠指標及失效概率計算錯誤。因此,如何避免雅可比矩陣的求解成了一個亟待解決的問題。

將有約束模型轉換為無約束模型的常用方法為罰函數法。內點罰函數法的罰因子逐步減小,常用于不等式約束;外點罰函數法的罰因子逐步增大,常用于等式約束。由于罰函數法是一種序列無約束極小化方法,所以收斂較慢,且兩種罰函數法的收斂性均依賴于罰因子的初值[13]。如果初始罰因子選取不當,就可能會導致兩種罰函數法中構造的目標函數均不收斂。因此,如何避免罰函數法初始罰因子的選取成了一個亟待解決的問題。

針對以上兩個技術難點,本文提出了一種采用增廣乘子法與模擬退火法的結構可靠性分析方法,通過增廣乘子法將等式約束優化模型轉換為無約束優化模型,采用模擬退火法求解結構的可靠指標。此外,本文研究了各參數的不確定度對可靠指標的影響,并與FOSM法和蒙特卡羅模擬(Monte Carlo simulation,MCS)法進行了對比,數值算例和懸臂梁算例的結果表明,本文方法迭代次數比MCS法少,且所得結果比FOSM法更接近于MCS法。

1 可靠性理論

正態分布的概率密度函數f(x)和累積分布函數F(x)的公式[14]分別為

(1)

(2)

式中μx和σx分別為變量x的均值和標準差。

拉科維茨·菲斯萊法可以實現正態分布到標準正態分布的轉換,公式[14]為

y=(x-μx)/σx

(3)

μy=x-φ-1[F(x)]σx

(4)

σy=φ{φ-1[F(x)]}/f(x)

(5)

(6)

(7)

式中:y為轉換后的x;μy和σy分別為變量y的均值和標準差;φ(y)為y的概率密度函數;φ(y)為y的累積分布函數;t為積分變量。

誤差函數erf(y)和互補誤差函數erfc(y)的公式[15]分別為

(8)

(9)

引入誤差函數后,累積分布函數φ(y)變為

(10)

可靠指標β和失效概率Pf的公式[14]分別為

β=(x-μx)/σx=μy/σy

(11)

(12)

變異系數V的公式[14]為

V=σx/μx

(13)

由大數定理中的Bernoulli定理可知,進行N次模擬之后,若功能函數g(x)<0的次數為nf,則直接抽樣蒙特卡羅法的失效概率Pf[14]為

(14)

式中:xu為第u次模擬時的變量;I[x]為示性函數,公式為

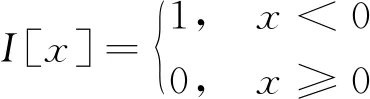
(15)

(16)

為提高直接抽樣蒙特卡羅法的精度,將抽樣中心改為MPP。重要抽樣蒙特卡羅法的失效概率Pf[14]為

(17)

式中fMPP(x)表示將概率密度函數f(x)中變量x的均值替換為MPP后的概率密度函數。

標準化正態空間中坐標原點到極限狀態面的最短距離就是可靠指標β[14],此時對應的極限狀態面上的點就是MPP[14]。

(18)

2 優化算法理論

2.1 等式約束的增廣乘子法理論

根據可靠性理論,可建立優化模型為

subject togj(X)=0,j=1,2,…,m

(19)

式中:M為適應度;X=[X1,X2,…,Xn];μv和σv分別為Xv的均值和標準差。

式(19)為具有m個等式約束gj(X)的模型,可以由增廣乘子法轉化為無約束優化模型,公式[13]為

(20)

式中:Mλ為無約束優化模型的適應度;r為外罰函數法的罰因子;λ=[λ1,λ2,…,λm],為拉格朗日乘子。式(20)右端第二項為懲罰項,第三項為乘子項。

使用增廣乘子法時,并不要求罰因子趨于無窮大,只需取一個比較大的值或按照一定的比例遞增[14]。此方法同時應用于外點罰函數法及拉格朗日乘子法,避開了外罰函數法的初始罰因子選取。

2.2 模擬退火法理論

1983年,IBM公司的Kirkpatrick等提出了一種基于物理學正則系統的模擬退火法,該算法使用了輔助分布和多重馬爾科夫鏈,且類似于吉布斯采樣器[16-18]。吉布斯分布又稱玻爾茲曼分布,表達式為

(21)

式中:i為迭代次數;P為概率;Z為配分函數或正則化常數;U(i)為勢能;k為玻爾茲曼常數;T為溫度;E(i)為系統的能量。

Creutz在研究物理學的伊辛模型時,提出了基于微正則系統的微正則退火法,其配分函數[18-19]為

(22)

式中:E0為初始能量值;ED為熱系統中具有能量交換能力的“妖”(Demon)的能量,更新規則為

(23)

式(21)中的溫度T有很多種計算方法。經過查閱相關資料,收集了以下3種常見的第i次迭代時的溫度Ti的計算方法。

(1)文獻[17]指出,若目標函數值的標準差為σf(x)、接受概率p>3σf(x),則溫度Ti為

(24)

(2)文獻[17]指出,為保證接受新解的概率大于設定值a0,應設定溫度Ti為

(25)

式中:Δ+為目標函數值上升的平均值;m1、m2分別為先前實驗中使目標函數下降、上升的解的數量。

(3)文獻[20]指出,設定一個足夠大的常數γ,使γ等于或者大于函數圖形的深度,則溫度Ti為

(26)

分析上述方法可知:方法(1)需要統計目標函數值的標準差,比較煩瑣;方法(2)需要設定初始概率值a0;方法(3)需要知道函數圖像的深度。由于以上3種方法的參數設置均比較困難,所以本文沒有采用。

模擬退火法利用μ-1原理[21]計算迭代步長,公式為

(27)

式中:gμ-1=[gμ-1,1,gμ-1,2,…,gμ-1,n]為計算迭代步長的中間變量;μ0=10100η,η=(i/imax)q,q為退火因子,必須大于0,q越大則退火速度越快[21];變量Xrand=[Xrand,1,Xrand,2,…,Xrand,n]與變量X的元素數量相同,且所有元素均是位于[-1,1]內的隨機數;sgn為符號函數。

模擬退火法利用Metropolis準則[13]來判斷是否接受新解,Metropolis準則為:當適應度的變化ΔMλ<0或隨機數p滿足一定的條件時,接受新解。p需要滿足的具體條件為

(28)

式中:ε是算法的精度;ε0是極小數常量,分母加上ε0是為了防止分母為零。在MATLAB軟件中,p由RAND函數生成,ε0由eps函數生成。

為避免式(28)中的指數函數計算,文獻[22]提出了Demon算法,具體如下:若ΔE≤D,則接受新解,同時更新Demon值D,即D=D-ΔE。但是,文獻[22]提出的Demon算法的初始Demon值如何設置,文獻[17]中并未記載,故本文未采用。

采用模擬退火法求解無約束優化問題的步驟如下。

步驟1 初始化X,并求出函數Mλ的函數值。

步驟2 開始迭代,設i為迭代次數。

步驟3 對每個Xν,計算迭代步長dXν=gμ-1,ν·(Bu,ν-Bl,ν),式中Bu,ν和Bl,ν分別為變量Xν的上下界。

步驟4 通過迭代步長求得新解X′=X+dX,如果X′不在范圍內則隨機賦予新值。

步驟5 首先求函數的變化值ΔMλ,然后根據Metropolis準則選擇是否接受新解。

步驟6 保留適應度最小的解。

步驟7 判斷是否達到循環終止條件。當i小于迭代上限imax時,返回步驟2;當i達到imax時,循環終止。

文獻[23]指出,為了在后期能夠跳出局部最優解,有學者提出了在后期提高溫度(即回火)的回火退火法,也有學者提出反復執行退火降溫和回火升溫的計算方法。若采用文獻[23]的回火退火法,則式(28)變為

(29)

本文將文獻[13]的增廣乘子法與文獻[13,21]的模擬退火法和文獻[23]的回火退火法結合,并將其應用于可靠指標的計算,分析結構的可靠性,本文方法的流程圖如圖1所示。

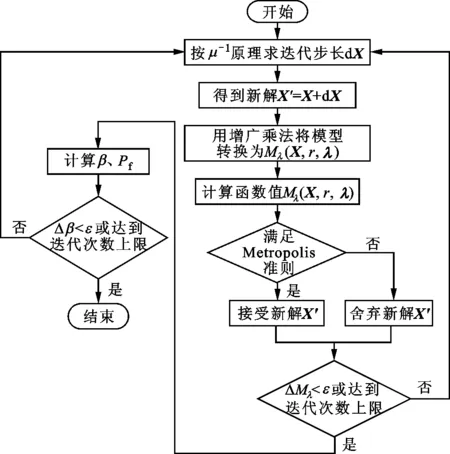
圖1 本文算法的流程圖

3 數值算例分析

設變量X=[X1,X2]服從正態分布,X1和X2均值分別為10和2.5,標準差分別為2和0.375,某個結構的功能函數g(X)為

(30)

設算法的終止條件為‖X(i)-X0‖/‖X0‖≤1×10-6,X0為最優解,X(i)為第i次迭代時的解。分別采用設計點法、JC法和簡化加權分位值法3種FOSM法[14]求解此問題,所得結果如下。

(1)3種方法的迭代次數均為12次,且功能函數g均等于8.689 9×10-12。

(2)3種方法所得可靠性參數幾乎相同,MPP約等于(11.185 490,1.654 912),可靠指標β≈2.330 217,失效概率Pf≈0.009 897。

(3)設計點法和JC法所得失效概率相同,而簡化加權分位值法的失效概率略小。文獻[14]指出,簡化加權分位值法的精度低于JC法,但是此次的計算結果表明,簡化加權分位值法與JC法的失效概率誤差僅為1×10-17。

取退火因子q=1,M0為當前函數值,Mv為最優函數值,設|M0-Mv|<1×10-6或迭代次數小于等于12作為終止條件。本文方法迭代4次得:MPP為(11.746 19,1.683 011),g=0.029 489,β=2.348 96,Pf=0.009 413。

設計點法、JC法和簡化加權分位值法3種FOSM法所得的可靠指標β=2.330 217,本文所得可靠指標β=2.348 96。兩種方法的可靠指標幾乎相同,證明本文方法可行。

經過1×107次模擬,直接抽樣蒙特卡羅法求得參數如下:β=2.346 2,Pf=0.009 5,σPf=3.064 7×10-5。

設重要抽樣蒙特卡羅法的抽樣中心為設計點(11.185 5,1.654 9),經過1×107次模擬,重要抽樣蒙特卡羅法求得參數如下:β=2.344 3,Pf=0.009 5,σPf=4.942 0×10-6。由此可見,與直接抽樣蒙特卡羅法相比,在模擬次數相同時,重要抽樣蒙特卡羅法的失效概率標準差σPf明顯偏小,說明重要抽樣蒙特卡羅法的改進效果較好。

將FOSM法、MCS法和本文方法的計算量和計算結果進行對比,結果見表1和表2,其中,FOSM法取JC法的數據,MCS法取重要抽樣蒙特卡羅法的數據。

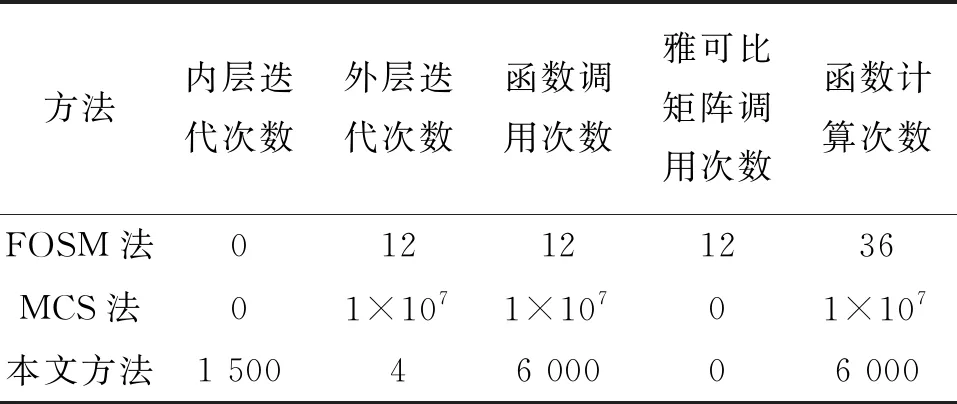
表1 數值算例下FOSM法、MCS法和本文方法

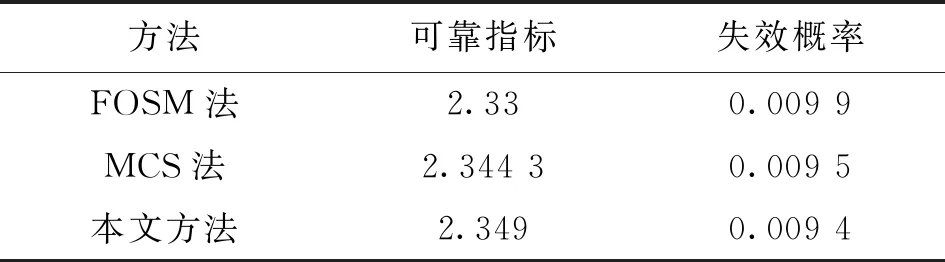
表2 數值算例下FOSM法、MCS法和本文方法

由表1和表2可以看出:本文方法的迭代次數少于MCS法,計算結果比FOSM法更接近MCS法。由此可得出,本文方法比MCS法效率更高,比FOSM法更精確。

在不同確定度下，X1、X2的均值μX1、μX2以及標準差σX1、σX2會有不同的變化范圍，此時通過本文方法計算得到的對應可靠指標β也會有不同的變化范圍和不確定度。不同不確定度下的μX1、μX2、σX1、σX2、β的變化范圍以及β的不確定度如表3和表4所示。

表3 不同均值不確定度下μX1、μX2、β的變化范圍及β的不確定度

表4 不同標準差不確定度下σX1、σX2、β的變化范圍及β的不確定度

由表3和表4可知均值和標準差的不確定度與β的不確定度之間的關系,如圖2所示。

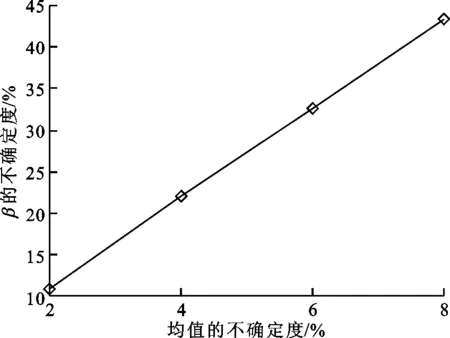
(a)均值的不確定度與β的不確定度的關系

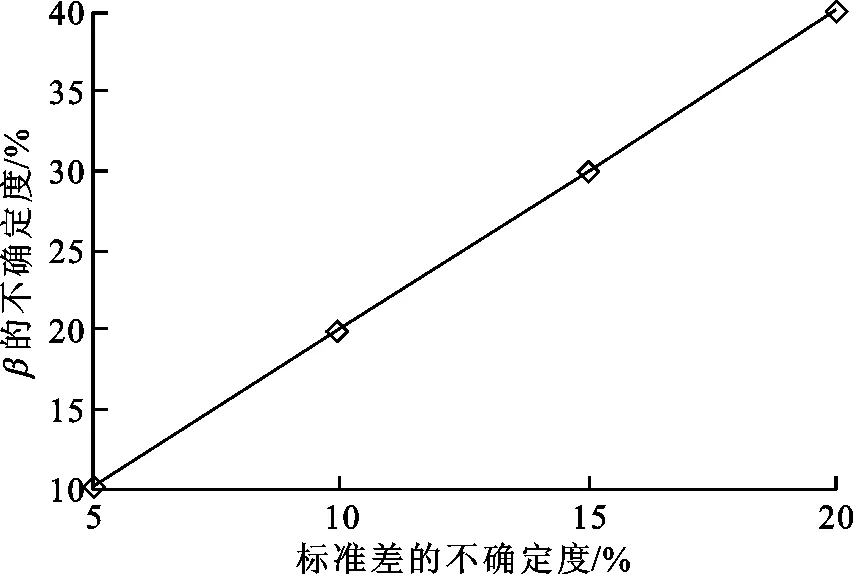
(b)標準差的不確定度與β的不確定度的關系圖2 均值和標準差的不確定度與β的不確定度的關系

對表3、表4、圖2進行分析,可得如下結論:

(1)β與均值呈正比關系,與標準差呈反比關系;

(2)β的不確定度與均值、標準差的不確定度分別呈現線性關系;

(3)均值的不確定度為8%時,β的不確定度為43.34%,標準差的不確定度為20%時,β的不確定度為40.07%,證明均值對β的影響比標準差對β的影響大一倍。

4 懸臂梁的可靠性分析

懸臂梁[24]長度為L,矩形橫截面的寬和高分別為b和h。懸臂梁末端承受的水平載荷和豎直載荷分別為Ph、Pv,末端許可撓度[ω]=3 mm。懸臂梁的材料為45號鋼,彈性模量E=210 GPa,屈服極限σs=350 MPa。此時,變量X=[b,h,L,Ph,Pv]。

設寬度b/mm～N(100,52),高度h/mm～N(200,52),Ph/kN∈[45,75],Pv/kN∈[22,28]。長度L的均值為1 000 mm,變異系數V=0.01,由式(13)可知L/mm～N(1 000,102)。根據正態分布的3σ準則可知,Ph/kN～N(60,52),Pv/kN～N(25,12)。

4.1 考慮撓度失效的可靠性分析

矩形截面的梁彎曲變形時,橫截面對中性軸的慣性矩IZ為

(31)

當懸臂梁的一端承受集中力Pv時,最大撓度ωmax為

(32)

所以,當懸臂梁的一端承受Ph、Pv兩個集中載荷時,產生的最大撓度為

(33)

考慮撓度失效時,功能函數g1為

(34)

由于此功能函數比較復雜,求導煩瑣,雅可比矩陣較難獲取,此處不再與FOSM法進行對比。

經過50次迭代,本文方法求得參數如下:MPP為(111.27,202.32,994.48,51.34,25.01),g1=-0.488 3,β=3.303 6,Pf=4.77×10-4。求解過程中β和Pf的變化如圖3所示。

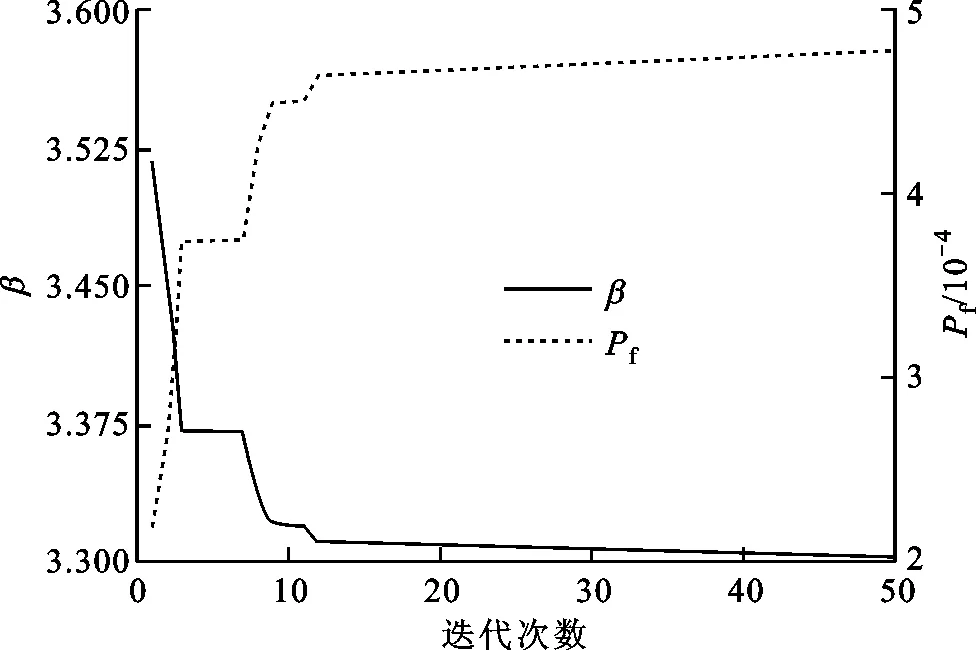
圖3 撓度失效求解過程中β和Pf的變化

由圖3可知,本文方法在前10次迭代中收斂較快,而在后40次迭代中收斂較慢。

4.2 考慮應力失效的可靠性分析

矩形截面的梁彎曲變形時,梁的抗彎截面系數WZ為

(35)

式中ymax為懸臂梁中性層到橫截面兩端的最大距離。

當懸臂梁一端承受Ph、Pv兩個集中載荷時,矩形截面上產生的最大應力σmax為

(36)

考慮應力失效時,功能函數g2為

(37)

經過1 000次迭代,JC法求得參數如下:MPP為(84.97,195.93,100 2.76,60.0,25.0),g2=48.756 6,β=3.126 1,Pf=8.857 2×10-4。

經過500次迭代,本文方法求得參數如下:MPP為(85.4,192.9,100 4.0,70.7,25.0),g2=-0.024 0,β=3.904 1,Pf=4.728 8×10-5。求解過程中β和Pf的變化如圖4所示。

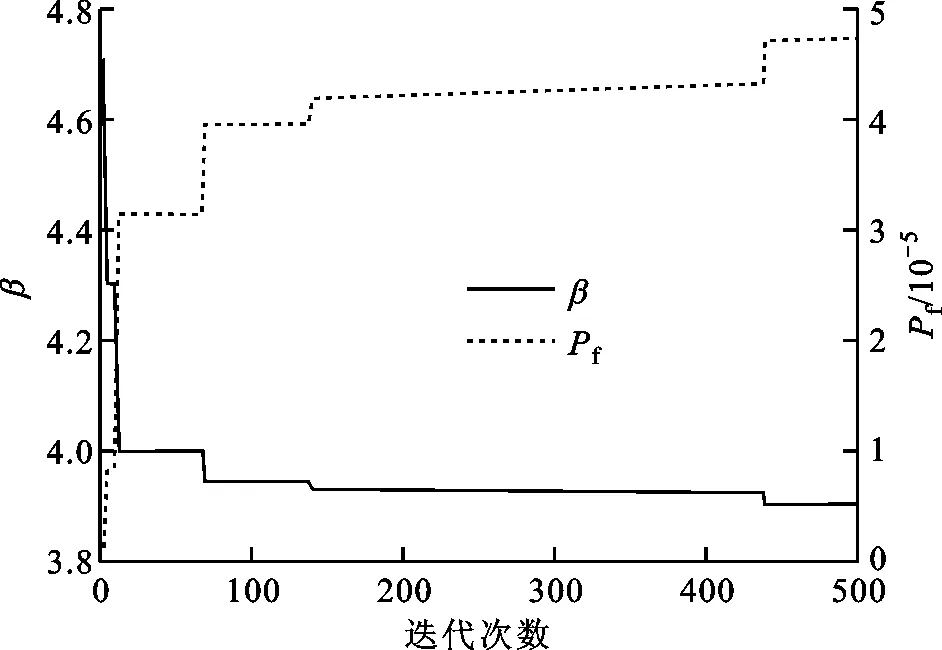
圖4 應力失效求解過程中β和Pf的變化

由圖4可知,本文方法在前70次迭代中收斂較快,而在后430次迭代中收斂較慢。

采用式(28)的模擬退火法及式(29)的回火退火法計算可靠指標,分別運行6次后得到兩組結果,分別為:3.896 6、3.920 5、3.983 8、3.911 4、3.931 4、3.949 6,以及3.914 0、3.988 3、3.916 4、3.955 7、3.952 9、3.889 2。可靠指標的統計參數見表5。

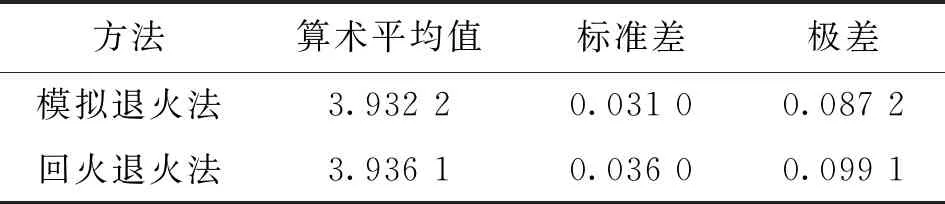
表5 可靠指標的統計參數

分析表5可知,在相同的迭代次數下,回火退火法的算術平均值、標準差和極差都較大,回火退火法的改進效果較差。這是因為回火退火法雖然提高了全局搜索能力,但是犧牲了局部搜索能力。如果將其應用于強欺騙性、多模態、多漏斗的函數,情況可能相反。

經過1×107次模擬,直接抽樣蒙特卡羅法求得參數如下:β=3.828 0,Pf=6.460 0×10-5,σPf=2.541 6×10-6。

設重要抽樣蒙特卡羅法的抽樣中心為設計點(84.97,195.93,1 002.7,60,25),經過1×107次模擬,重要抽樣蒙特卡羅法求得參數如下:β=3.835 4,Pf=6.267 7×10-5,σPf=4.120 8×10-8。與直接抽樣蒙特卡羅法相比,在模擬次數相同時,重要抽樣法的失效概率標準差σPf明顯偏小,說明重要抽樣蒙特卡羅法的改進效果較好。

FOSM法、MCS法和本文方法的計算量見表6,計算結果見表7。

分析表6和表7可知,本文方法的迭代次數比MCS法更少,所以本文方法比MCS法效率更高。FOSM法的失效概率與MCS法相比相差一個數量級,誤差非常大,而本文算法的失效概率4.8×10-5更接近MCS法的失效概率6.3×10-5,說明本文方法比FOSM法更精確。由于本文方法和MCS法都不需要計算雅可比矩陣,所以FOSM法的結果誤差較大極有可能是由于雅可比矩陣條件數過大導致的。

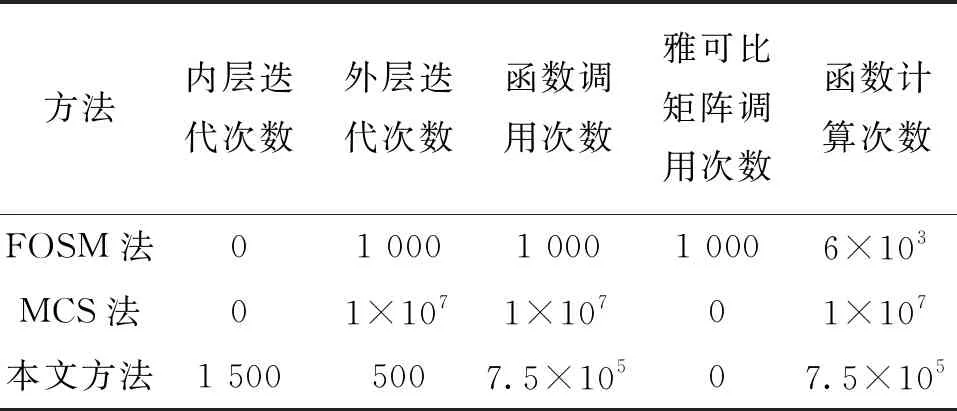
表6 懸梁臂可靠性分析時FOSM法、MCS法和本文方法的計算量

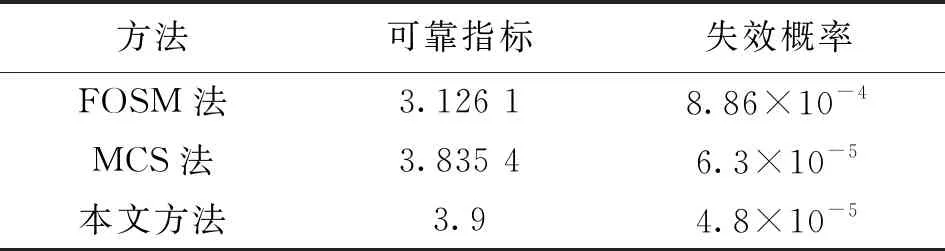
表7 懸梁臂可靠性分析時FOSM法、MCS法和本文方法的計算結果

根據考慮撓度和應力失效的雙失效模式系統的迭代結果可知,撓度的失效概率比應力大,且雙失效模式的串聯系統的失效概率Pf=5.24×10-4。

4.3 均值的不確定度對可靠指標的影響

改變均值的不確定度,并保持標準差不變,本文方法所得的可靠指標及可靠指標的不確定度見表8。

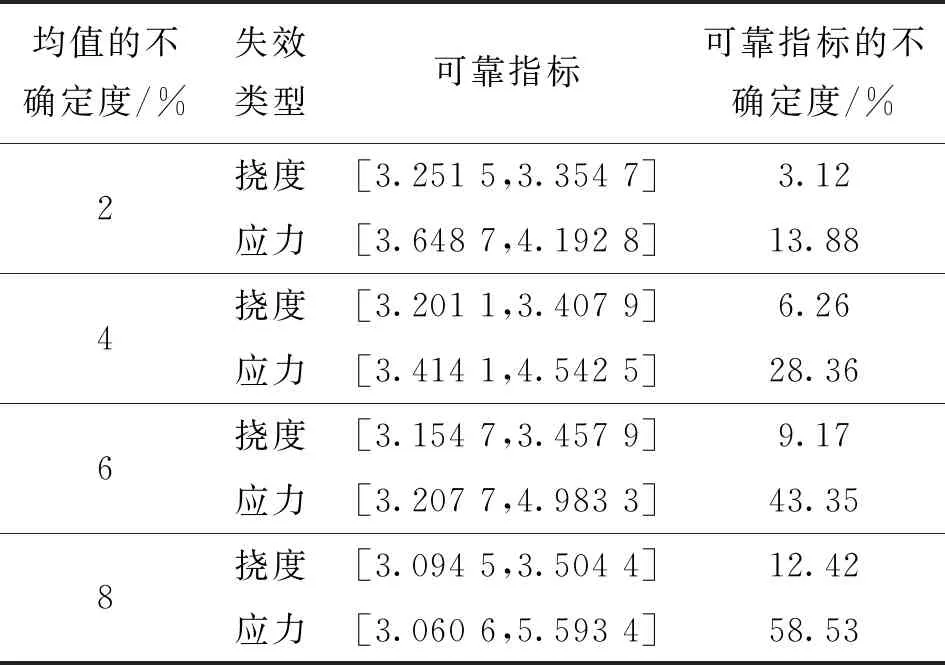
表8 不同均值不確定度下的可靠指標及可靠指標的不確定度

由表8可知均值的不確定度與撓度失效和應力失效可靠指標的不確定度之間的對應關系,如圖5所示。

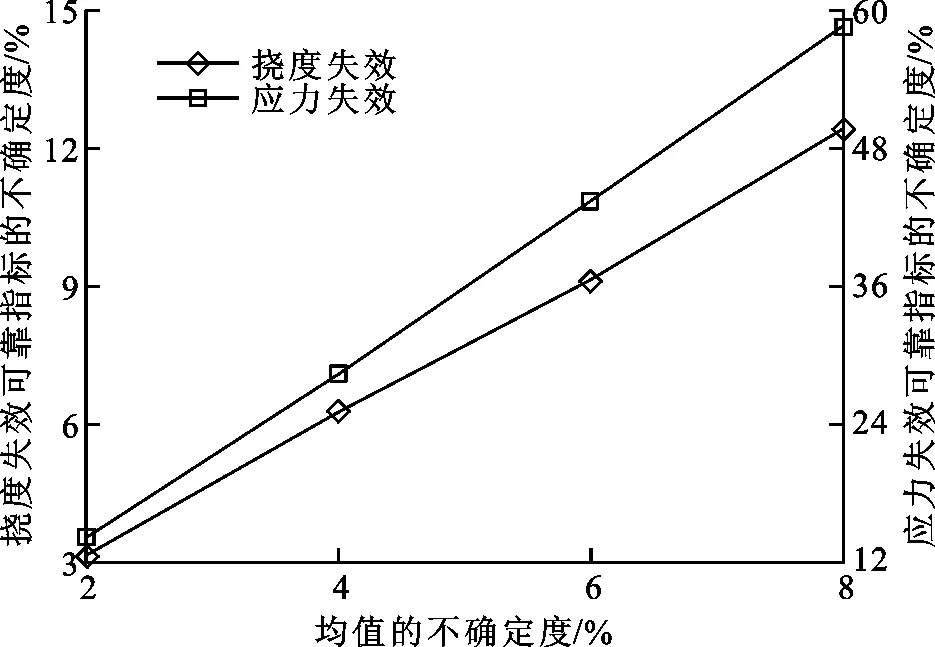
圖5 可靠指標受均值不確定度的影響

由表8和圖5可以看出:

(1)在均值不確定度為2%時,撓度失效可靠指標的不確定度為3.12%,應力失效可靠指標的不確定度為13.88%,撓度與應力可靠指標的不確定度分別呈1.5倍和6倍的關系;

(2)觀察其他均值不確定度的情況可看出,撓度與應力可靠指標的不確定度分別呈線性關系,而且分別呈近似1.5倍和5倍的關系;

(3)均值的不確定度對應力的影響是對撓度的影響的4～5倍。

5 結 論

(1)FOSM法需要計算雅可比矩陣,而病態的雅可比矩陣會導致計算結果誤差大大增加。分析懸臂梁應力失效時,FOSM法的結果異于MCS法和本文方法,這極有可能是由雅可比矩陣為病態矩陣引起的。

(2)傳統的罰函數法的收斂性依賴于罰因子初始值的選取,而本文方法的收斂性并不依賴于拉格朗日乘子和罰因子的初始值。本文采用增廣乘子法將有約束優化模型轉換成無約束優化問題,成功避免了罰因子初始值的選取。

(3)本文方法的迭代次數介于FOSM法和MCS法之間,且結果更接近于MCS法。本文方法有望拓展到具有多個極限狀態方程的多學科可靠性分析及優化問題中。