考慮模式切換頻率的多模式混合動力汽車參數優化

黃康,王強,邱明明,張怡然,劉澤鏈,耿麗珍

(1.合肥工業大學機械工程學院,230009,合肥;2.奇瑞汽車股份有限公司,241000,安徽蕪湖)

混合動力汽車是未來新能源汽車發展的一個趨勢,伴隨著在此領域內的深入研究,越來越多的能量管理方法被提出[1],但是從實用性的角度來看,最基礎的邏輯門限能量管理策略卻得到了更為廣泛的應用。從能量管理策略的角度來說,諸多新穎的能量管理策略以及優化策略實則回歸到本質上是對邏輯門限能量管理策略的優化和擴展[2-6],因此從參數優化的角度來說,往往在以經濟性或者動力性為目標時均是以邏輯門限能量管理策略作為基礎,進行優化求解。劉永剛等以動力性為約束,通過油電轉化系數以經濟性為目標,利用模擬退火粒子群算法對邏輯門限能量管理策略中的幾個閾值和動力部件的功率進行了優化[7];張松等采用遺傳算法和粒子群算法針對經濟性和尾氣排放,優化了邏輯門限控制策略中的油門開度、車速等5個參數[8];Zhang等用NSGAII算法,以整合后帶權重的油耗以及尾氣排放為目標,優化了電機功率等參數并在ADVISOR里面進行了仿真驗證[9];Xu等對一串聯式混合動力汽車的電機和主減速器進行了優化,尤其強調對二者進行協同優化,并仿真驗證了有效性[10];Wu等以燃油經濟性為優化目標,通過粒子群算法優化CD-CS控制參數,在保證動力性能的同時優化了經濟性[11]。上述研究均只單純考慮了經濟性和動力性因素,而未考慮優化參數使得車輛工作在邏輯門限的邊界附近時對車輛工作的穩定性、工作模式切換的頻繁性造成的影響。

本文以國家重大專項中的新型高性價比乘用車混合動力汽車為優化對象,以其在新標歐洲循環測試(NEDC)工況下的經濟性、加速性能以及模式區分度為優化目標,通過多目標粒子群算法(MOPSO)對其三檔傳動比、電機2的單級減速器傳動比以及典型邏輯門限能量管理策略中的兩個閾值同時進行優化,在優先考慮動力性和經濟性的優化的前提下,提出了模式區分度的概念作為優化目標函數同時對3個目標進行優化,保證了新型多模式混合動力汽車模式的穩定性,可避免其在典型工作點下頻繁進行模式切換,進一步提高了車輛運行的穩定性與舒適性。

1 動力總成結構與整車參數

目前國內的汽車企業傾向于在典型的混聯式混合動力構型上增加離合、鎖止器等以增加動力總成的模式可選擇性,以充分利用各個動力部件的高效工作區,提高整體經濟性,但這無疑增加了能量管理和參數優化的難度。本文結構來源于國家重大專項PHEV項目中給定結構,動力總成結構如圖1所示。該結構采用單排行星輪,發動機輸出連接到了行星輪的太陽輪,并增加了鎖止器B1,電機1轉子直接輸出到行星輪的齒圈上,離合器C1用于控制行星耦合機構(ePGS)中發動機與電機1的耦合模式,離合器C2用于控制ePGS模塊同電機2耦合與否,電機2通過單級減速器輸出,并增加采用了三檔變速箱,利用C3和同步器進行換檔控制,主要參數如表1所示。

2 邏輯門限值能量管理策略

傳統的基于邏輯門限的能量管理策略具有可靠性高、運算量小的特點,得到了廣泛的實際應用。由于本文動力總成結構較為復雜,可選的邏輯門劃分方式較多,本文根據選用動力總成構型,參考各個動力部件的高效工作區間,采用了如圖2所示的邏輯門限劃分方式,圖中1～6分別對應于表2中模式1～6。圖中橫坐標為耦合軸上的轉速,縱坐標為耦合后的轉矩;左右分界線為發動機的怠速轉速,分界線左側1和2為純電模式,右側從下往上的實線依次為單電機與雙電機分界線(1′和2′分界線)、發動機啟動分界線(2′和3分界線)、發動機最佳工作曲線(3和4分界線)、發動機與電機1耦合分界線(3和4分界線),發動機最佳工作曲線與電機1和電機2外特性曲線耦合分界線(4和5分界線)、發動機最佳工作曲線與電機1和電機2外特性曲線耦合線(5和6分界線)、發動機外特性曲線與電機1和電機2外特性線曲線耦合線。表2為邏輯門限能量管理策略中各模式的代號及說明。

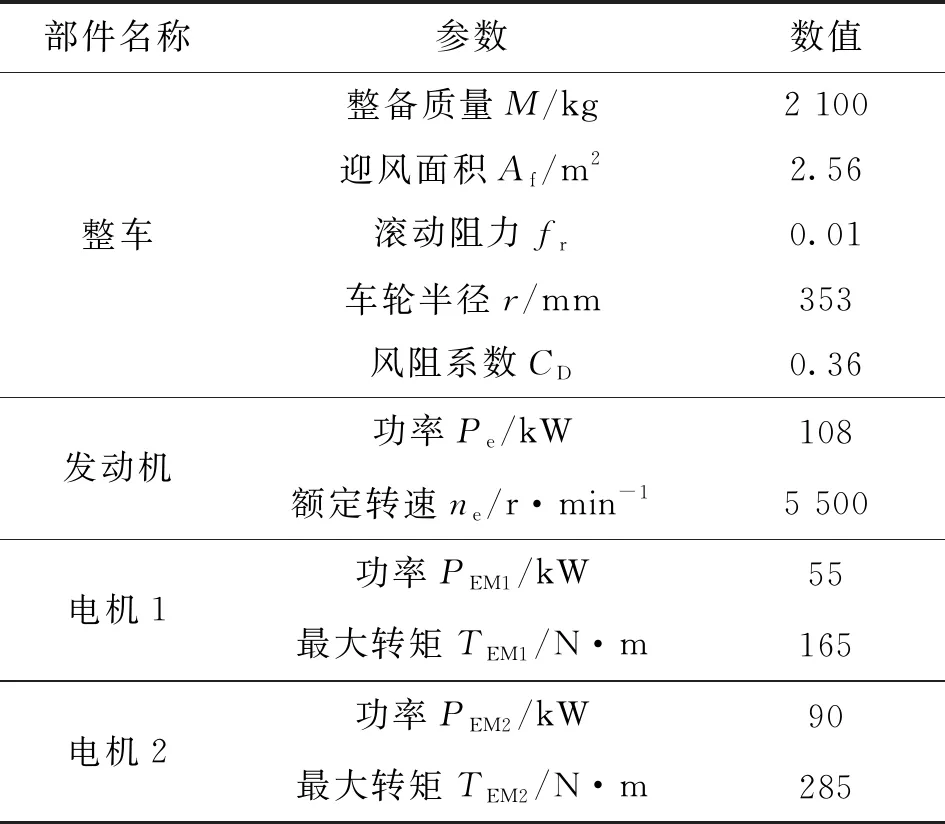
表1 整車及動力源主要參數

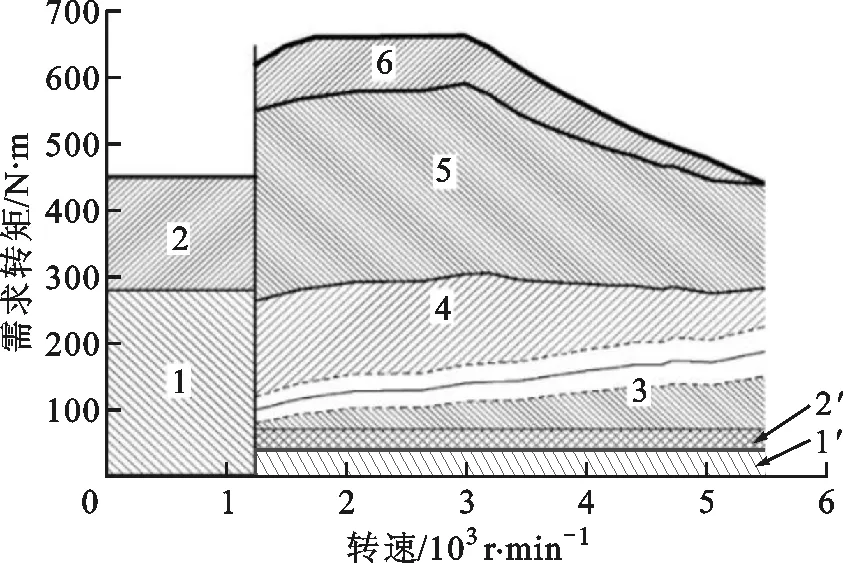
圖2 混合動力模式能量管理策略

3 多目標粒子群優化算法

多目標的粒子群算法以Coello等在2004年提出的方法[12]最具有代表性,得到了廣泛的認可。與單目標的粒子群優化算法不同的是,多目標之間相互矛盾,沒有一個最優解,因此在多目標粒子群優化里面,每個粒子需要單獨從保存Archive集中選擇各自的全局最優點,而對于個體最優點,則通過Archive密度信息進行選擇。不論是多目標優化還是單目標優化,粒子群算法更新公式為

(1)

式中:r1和r2為(0,1)內的隨機數,服從平均分布;c1和c2為加速系數,通常在(0,2)內取值,c1為個體加速系數,c2為全局加速系數,分別表示粒子對個體認知和社會知識的信任程度;下標id表示第i個變量的個體極值的第d維;下標gd表示全局最優解的第d維。

3.1 目標函數

本文選取了傳統的經濟性和動力性作為優化目標,并提出了區分度的概念,作為第3個優化目標。

表2 邏輯門限能量管理策略

注:CSOC表示電池荷電狀態(SOC)。

(1)經濟性目標函數。本文不以油電轉化系數將油耗轉化為電耗,或者電耗轉化為油耗進行代換,這種方法實際在不考慮溫度對電池的影響的情況下,也只是一個常系數而已,因而本文直觀利用當前的電價和油價來設定經濟性目標的適應度函數如下

f1=pfff+pefe

(2)

式中:pf為油價,取6.75元/L,pe為電價,取0.565 3元/(kW·h);ff為一個NEDC循環下的燃油消耗量;fe為一個NEDC循環下的電量消耗。所涉及的優化參數有3檔傳動比。

(2)動力性目標函數。由于采用了3檔變速箱,并且要求100 km/h前只換一次檔,不適合以百公里加速時間作為優化的適應度函數,在此選取了從0到設計極速(170 km/h)的加速時間作為優化的目標函數。

(3)模式區分度目標函數。文獻[13-15]中分別采用了PID、模糊等方法,通過電機補償,對離合器的轉速和電機轉速,以及發動機油門開度進行PID控制,來解決在車輛運行中模式切換時存在的問題,文獻[13]的結果表明模式切換的平順性是動力性和舒適性的一對矛盾解,即若要增加舒適性,則會犧牲一部分動力性;若要保證動力性,則模式切換的沖擊會更大。也有通過模糊的方法來解決模式與模式之間的邊界問題,但這些方法都為對邊界點可能出現的位置進行優化,不能解決工作在模式與模式分界點時造成的模式頻繁切換問題,因此本文針對這個問題,提出了模式與模式之間區分度的概念,即期望通過對結構參數和邏輯門控制參數的優化,使得模式的典型工作點遠離模式與模式的邊界,即典型的工作區間不應該出現在模式的邊界上。尤其針對本文涉及的這種多模式的混合動力汽車,由于模式較多,模式邊界也更為復雜,由此本文提出了第3個目標函數。

本文選取了NEDC工況作該車的典型工作工況,將其在邏輯門策略中的工作位置視作典型的工作點。根據汽車理論,行駛阻力的定義為

積極推進重大戰略研究及前期工作。邀請知名院士專家赴黃土高原地區考察，深入研究黃河水沙情勢變化規律。組織人員實地查勘南水北調西線工程社會環境等因素，對南水北調西線一期工程項目建議書進行補充完善。加快古賢水利樞紐立項進程，完成其環境影響評價專題報告并上報水利部。深入開展黃河下游河道改造與灘區治理研究，深化黑山峽河段開發論證。完成黃河東平湖蓄滯洪區治理與沁河下游河道治理工程可研報告并通過水利部審查。經過9年的不懈努力，黃藏寺水利樞紐項目建議書獲得國家發改委批復，在完善黑河水量調度工程措施上邁出可喜一步。

(3)

式中:G為汽車的重力;f為滾動阻力系數;i為道路坡度;CD為空氣阻力系數;A為迎風面積;ua為行駛速度;δ為汽車旋轉質量換算系數。

通過式(4)得到需求轉矩為

(4)

式中:ig為當前檔位傳動比;i0為主減傳動比;r為車輪半徑。

通過式(5)得到當前的需求轉速為

(5)

根據需求轉矩和轉速就可以在圖6中得到對應的邏輯門的工作點,為了使得工作點離模式的邊界盡可能遠,設定了如下區分度目標函數

(6)

式中:Ti為實際轉矩;Tk和Tk′分別為所在區域的邊界值;負號是因為需要求最大值,做了取負處理;n為NEDC工況的采樣點,本文采樣間隔取為1 s,n即為1 180;ωj為對應模式邊界的權重系數。具體來說,希望盡可能避免工作在模式2和模式3的邊界附近,因為此處需要啟動發動機,又要求最大值,經過多次調整,選取權重系數為0.9,同理模式5與模式6之間的邊界也選取權重系數為0.9,因為此處涉及到離合器C1的變換,其余的權重系數取1。注意到,對于低速區的純電模式向高速區過渡的邊界同樣涉及到發動機啟動,在觀察NEDC工作點分布后,工作點實際為從低速區向高速區的單方向跨越,優化此速度分界線對結果的影響不大,故略去對此處的考慮。

3.2 優化參數和約束函數

選取3檔傳動比分別對應的ig1、ig2、ig3,主減速器傳動比igf,電機2的單級減速器的傳動比ige,以及模式1與模式2的分界線的設定參數k1,模式2與模式3的分界線參數k2共7個參數作為優化參數,即有

(7)

(8)

根據最大爬坡要求,可以得到最大傳動比約束條件,即有

(9)

根據等比數列偏置,得到約束條件

(10)

并由100 km/h前換一次檔得到二檔約束條件

(11)

兩個模式分界線的約束條件k1、k2的取值范圍由在5 500 r·min-1時的電機轉矩進行確定,根據設計由模式2進入模式3時,希望由兩個電機提供轉矩啟動發動機,以增加模式切換的平順性,若采用電機2單獨工作,電機1單獨啟動發動機,從模式2向模式3切換時,需要閉合離合器C2,會造成沖擊,因此考慮將行星輪的行星架和齒圈作為輸入,發動機啟動轉矩作為負載,利用兩個電機啟動發動機。根據行星輪的轉矩特性,即有

Tr∶Tr∶Tr=1∶α∶-(1+α)

(12)

需要電機保留富余的轉矩,進而得到k1、k2的約束條件,最終選定優化參數范圍如表3所示。

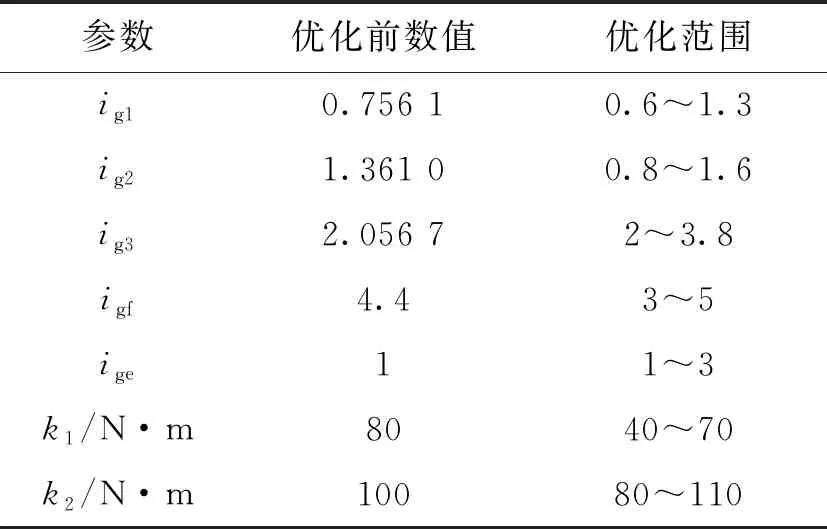
表3 優化參數范圍

3.3 車輛模型以及控制策略模型

AVLCruise軟件作為一款常用的車輛仿真軟件,建模方法和模塊化的建模手段使得不同項目組可以對模型進行方便快捷的整合,并快速搭建各種復雜的動力傳動系統模型,同時進行正向或逆向仿真分析。本文通過Cruise建立整車模型,利用Interface接口在Simulink搭建控制策略進行聯合仿真,Cruise的整車模型如圖3所示,控制策略模型如圖4所示。

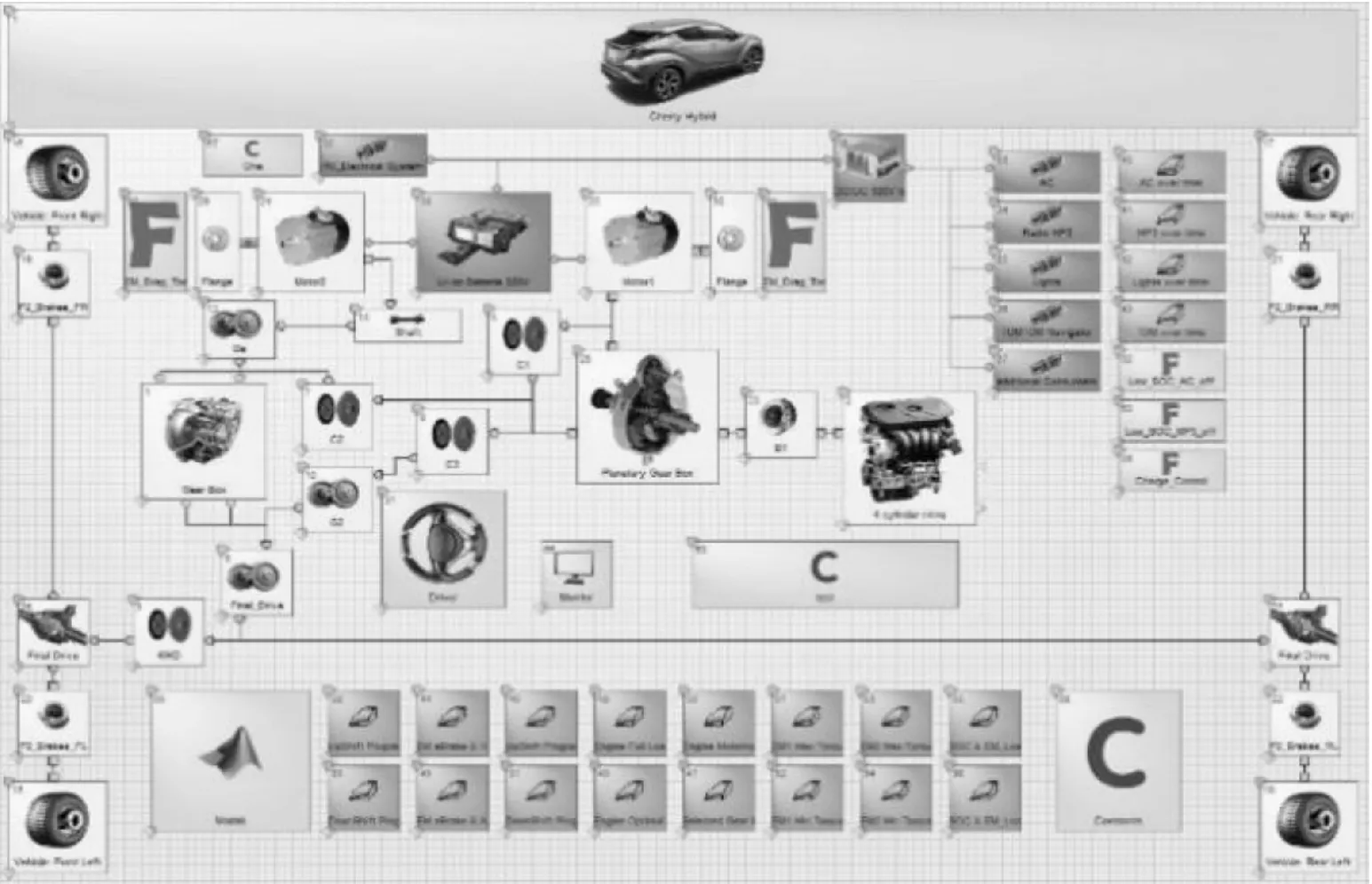
圖3 Cruise整車模型

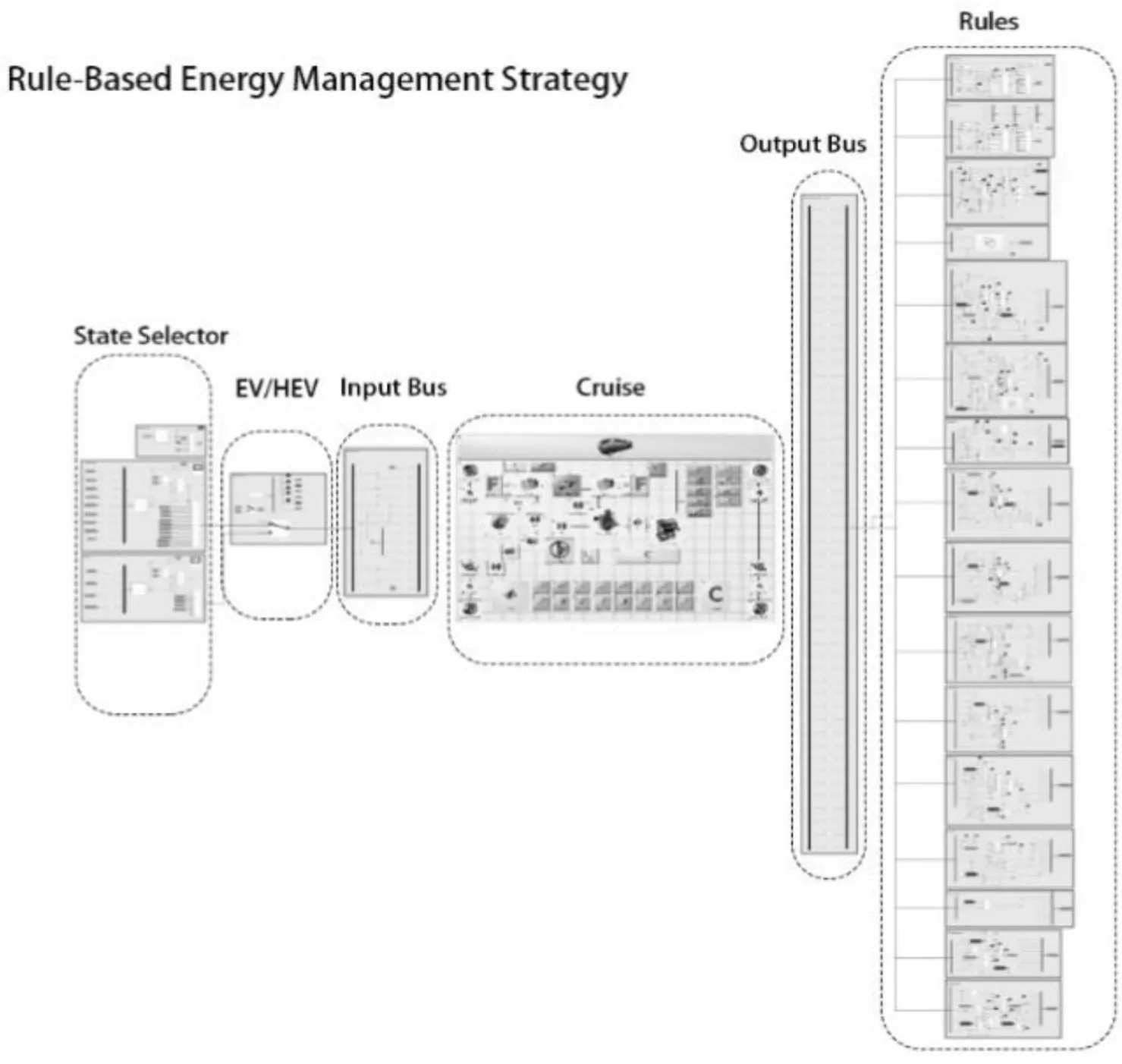
圖4 Simulink控制模型

4 優化結果與仿真分析

根據本次優化的目標和參數,優化的數學模型如下

(13)

根據計算精度需求,本文選取了50個粒子,選擇初始ω值為0.9,并給予一個每次迭代的衰減值0.99,這樣能保證在60次迭代的時候ω為0.45,即能保證初始的搜索速度和后期的搜索精度。個體加速系數c1設置為1,全局加速系數c2設置為2,進行60次迭代得到的優化結果如圖5所示。圖5a中的點均為可行解,近似分布在擬合曲面上。

單從動力性和經濟性的角度看,這個分布和傳統的雙目標優化的解的分布方式是一致的,即表現為一對明顯的矛盾解,表明優化結果正確繼承了雙目標優化的結果,但是同時還受到了區分度的有效約束。

由于這些解均為可行解,但本文考慮到動力性不宜太差,區分度良好,要求在280 N·m以上,經濟性有盡量好的傾向,故選取了3組解,并對3組可行解在搭建好的Simulink和Cruise平臺上進行了仿真,仿真結果如圖6～8所示。

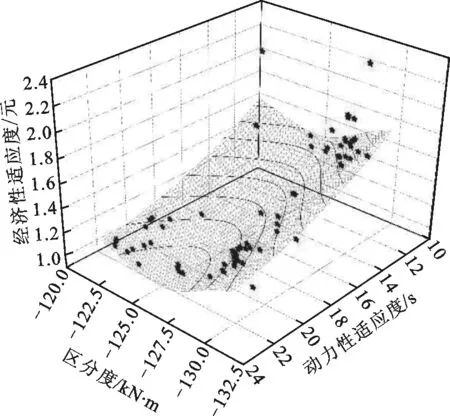
(a)粒子群優化結果三維圖

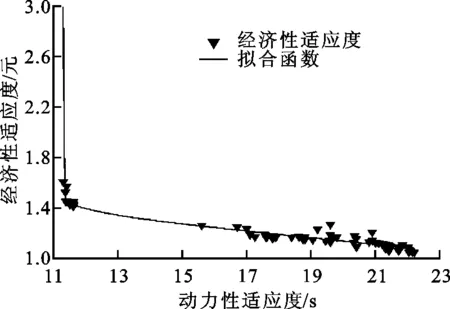
(b)動力性與經濟性適應度的關聯性圖5 粒子群優化結果

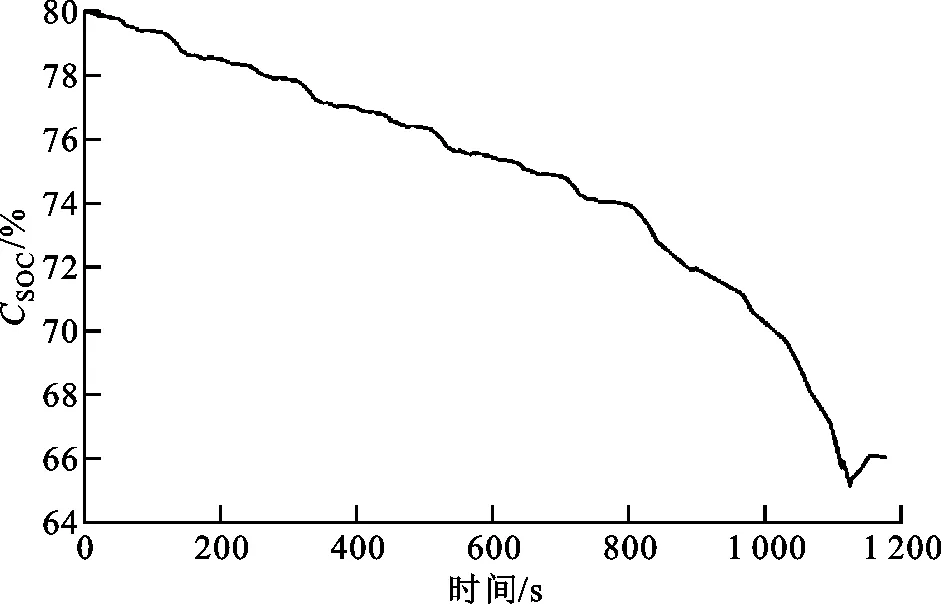
(a)SOC變化曲線

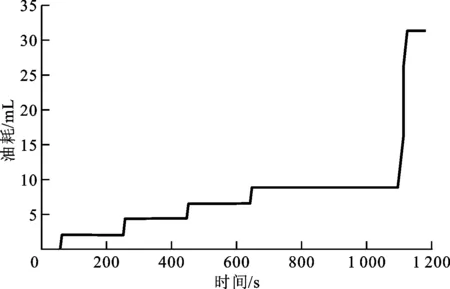
(b)油耗曲線

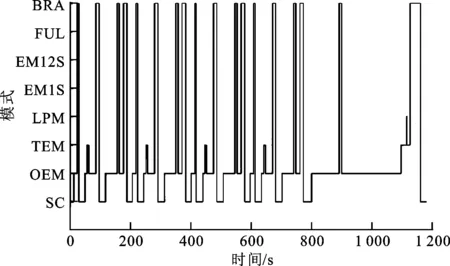
(c)模式變化圖

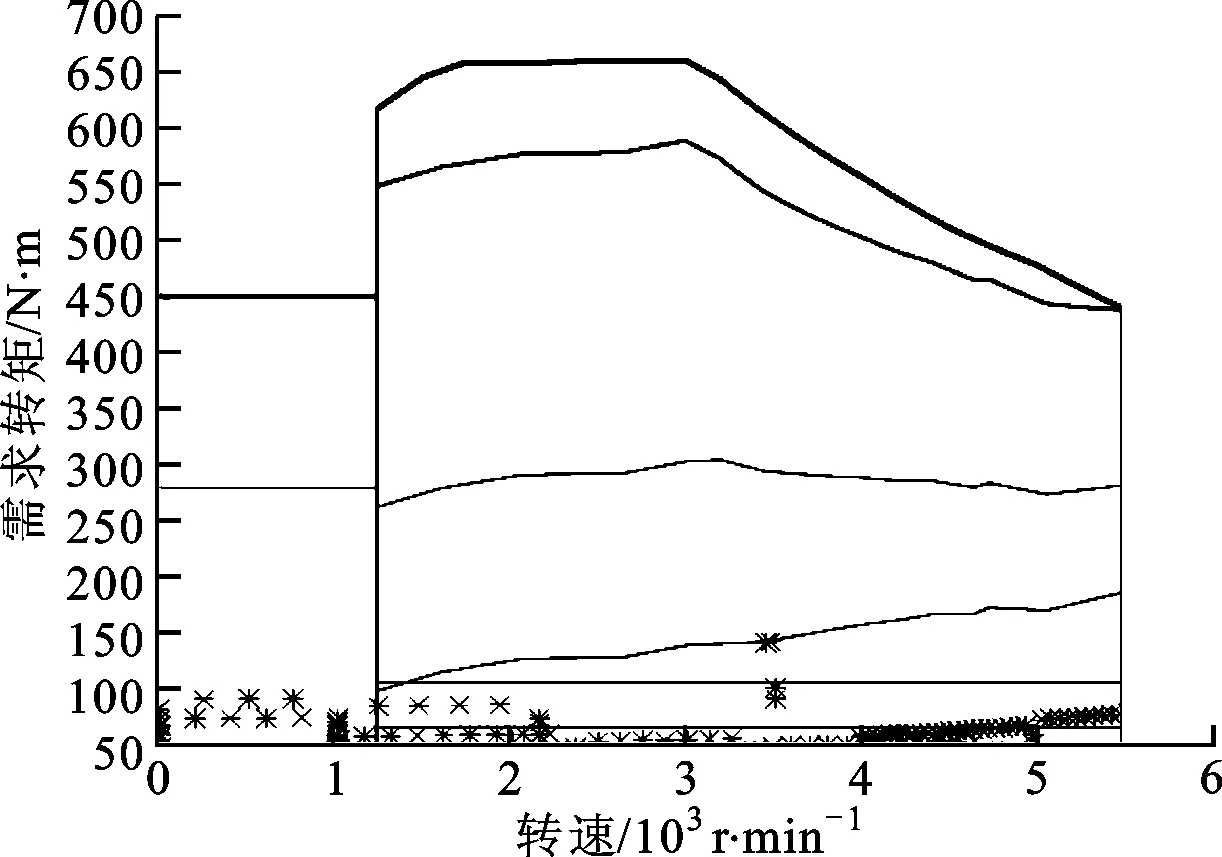
(d)工作點分布圖ig1=1.281 1;ig2=2.177 8;ig3=2.966 5;igf=3.044 3;ige=1;k1=70 N·m;k2=108.14 N·m圖6 解1仿真結果

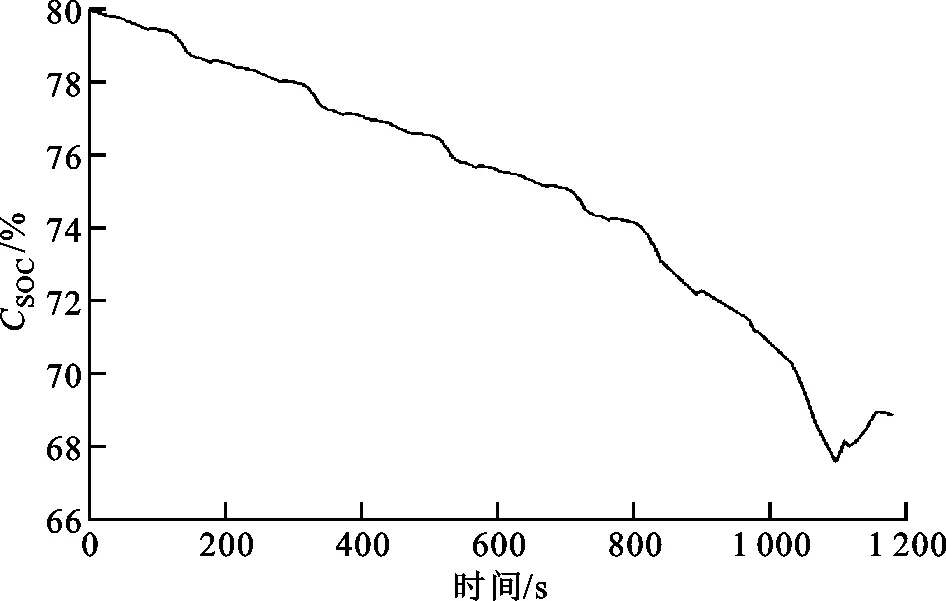
(a)SOC變化曲線

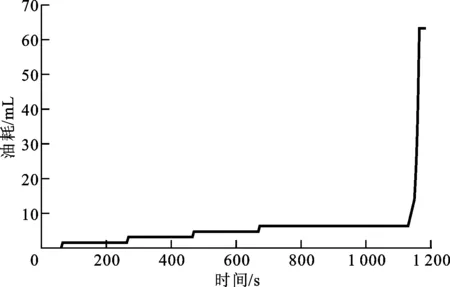
(b)油耗曲線

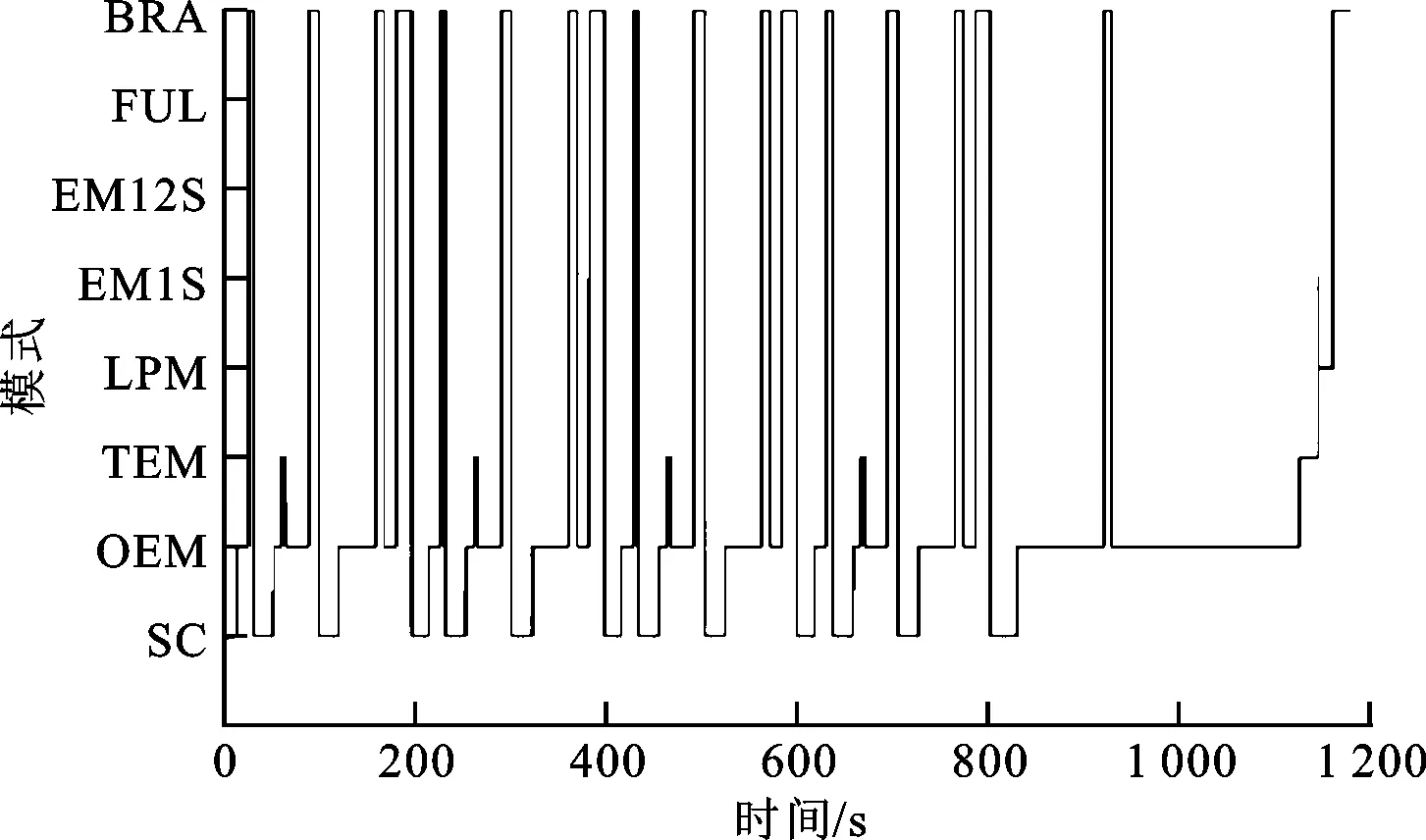
(c)模式變化圖

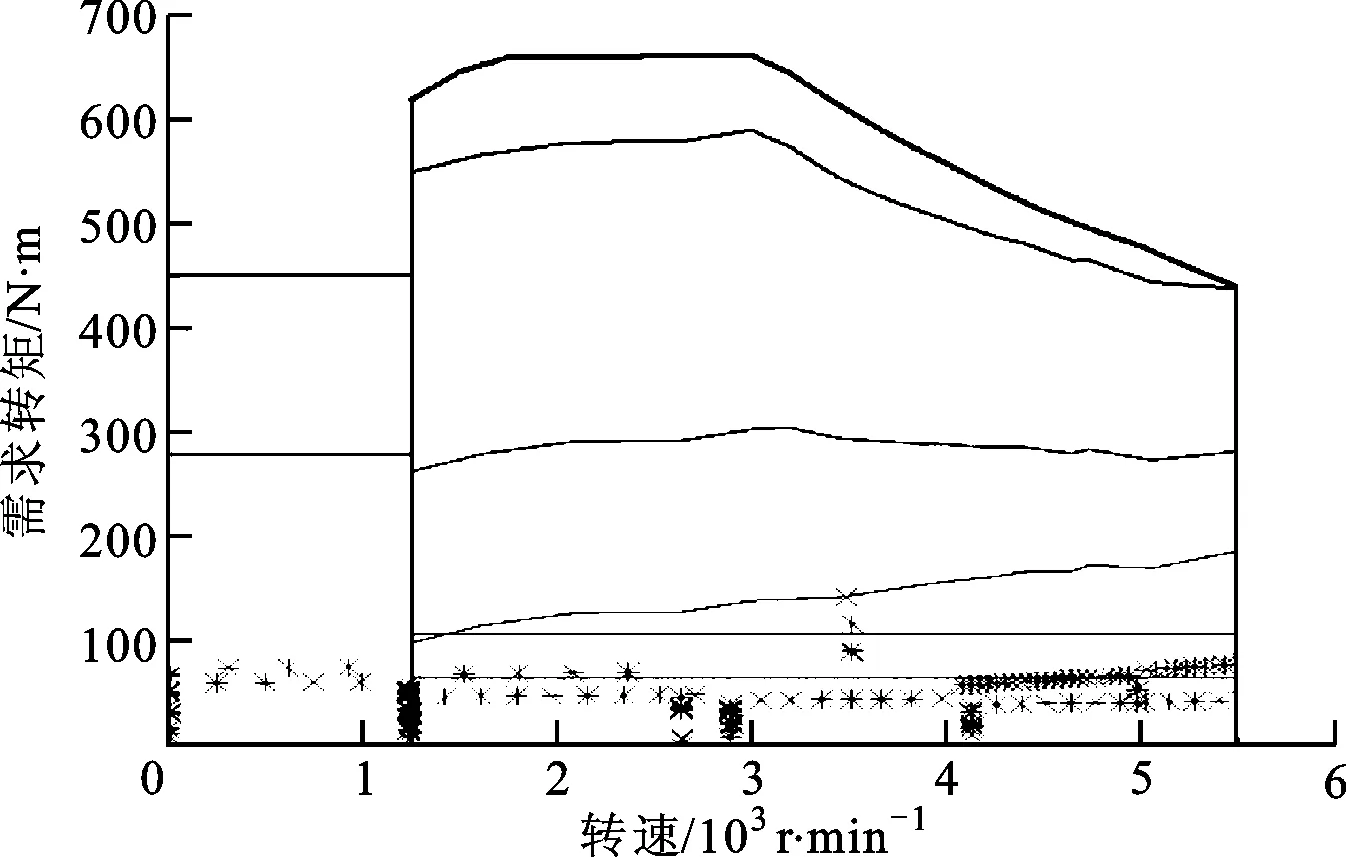
(d)工作點分布圖ig1=1.3;ig2=2.21;ig3=3.666 7;igf=3;ige=1.51;k1=70 N·m;k2=88.412 7 N·m圖7 解2仿真結果

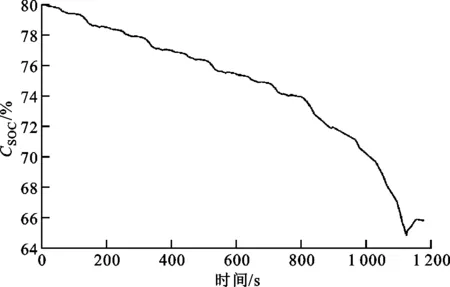
(a)SOC變化曲線

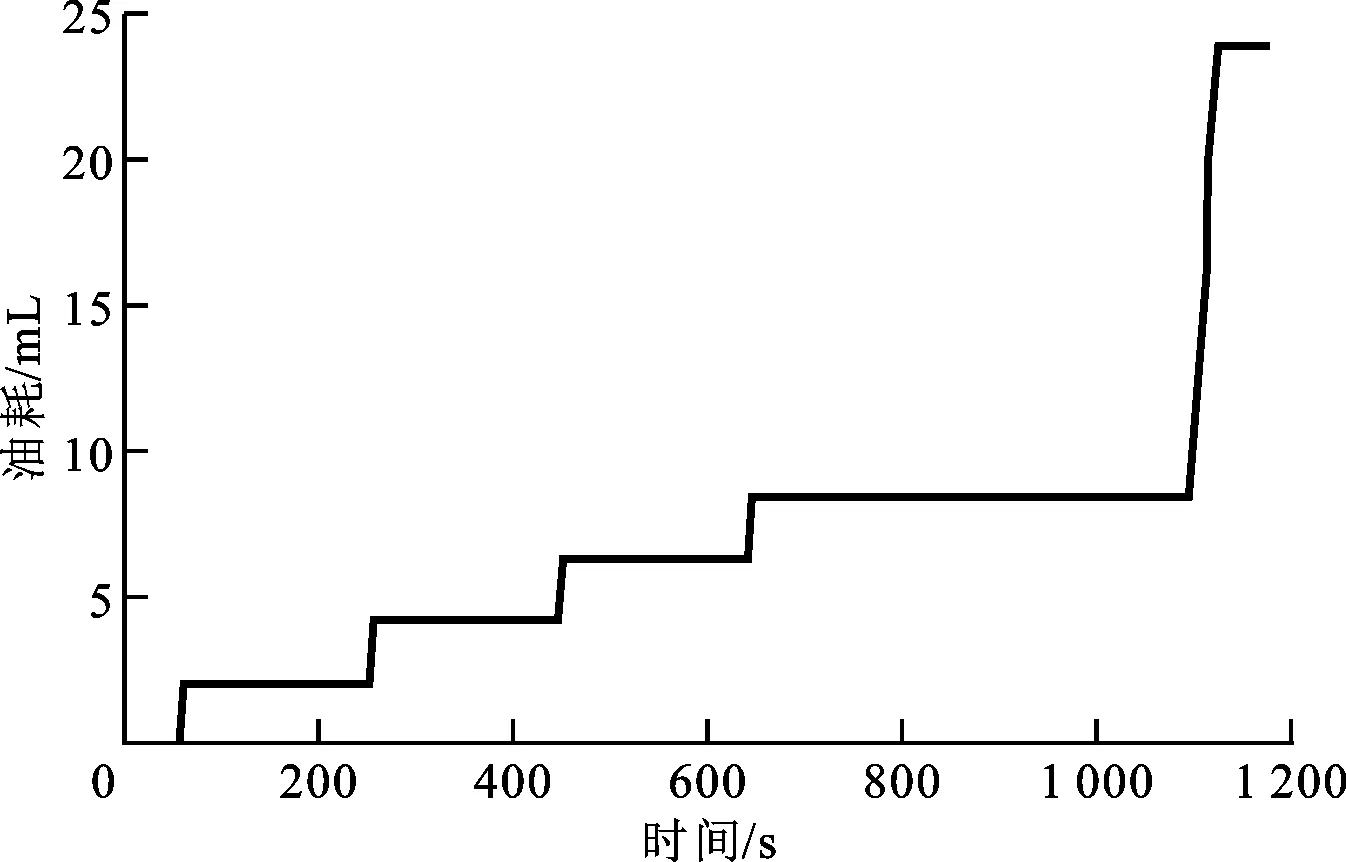
(b)油耗曲線

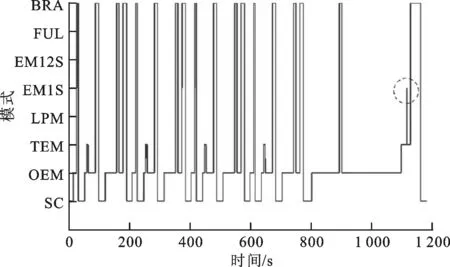
(c)模式變化圖

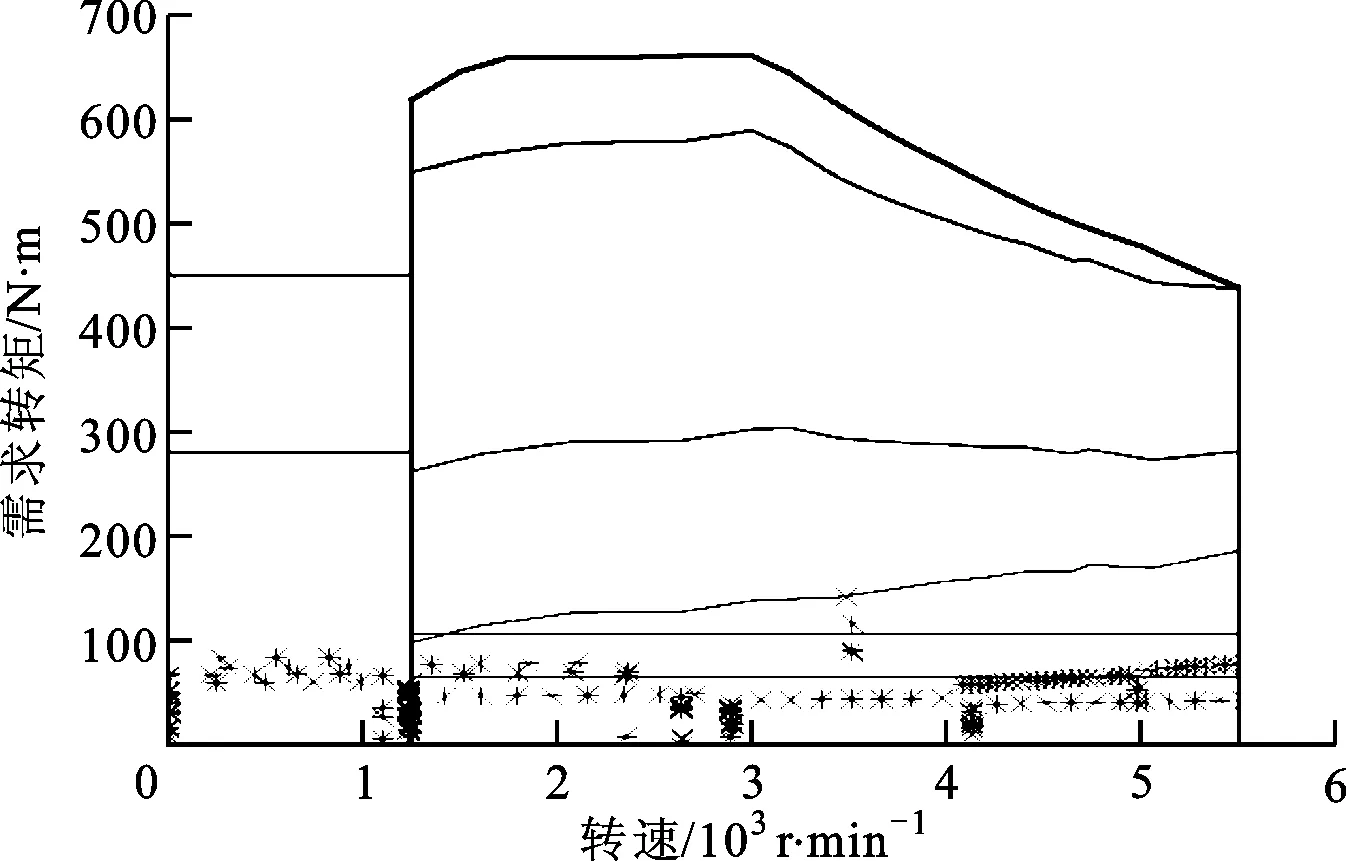
(d)工作點分布圖ig1=0.524 5;ig2=0.891 6;ig3=2.508 1;igf=4.385 1;ige=2.987 6;k1=66.59 N·m;k2=106.89 N·m圖8 解3仿真結果

由圖6～8可知,從0到170 km/h,解1的加速時間為11.625 4 s,經濟性適應度為1.445元,解2的加速時間為11.616 6 s,經濟性適應度為1.607 1元,解3的加速時間為21.435 4 s,經濟性適應度為1.055 9元。

注意到大多數工作點都在轉矩較低的范圍內,這是因為本車設計之初對百公里加速進行了要求,所選電機功率較大,而在NEDC工況內所選電機的性能并不完全發揮。另外注意到,在圖8c中虛線圈出的區域,模式從OEM→EM1S→LPM→OEM,在較短的時間(約5 s)內進行了切換,而在解1中也存在這一現象,但是模式并沒有調到EM1S,只是進入了LPM以提供短時間加速的動力性需求,這就是本文引入區分度概念的原因,控制傳動比參數和2個閾值,實際上是控制了工作點在邏輯門控制策略中的位置,以防止頻繁地工作在邊界上造成頻繁的模式切換。同時,本文也繼承了傳統優化思路,保證了燃油經濟性和整車的動力性能,其中解3僅因為說明區分度作用而給出,故不作對比,其余兩解與原結果對比的結果如表4所示。

為了驗證這套優化理論的通用性,本文利用JC08工況進行了仿真驗證,仿真結果如圖9～圖12所示。

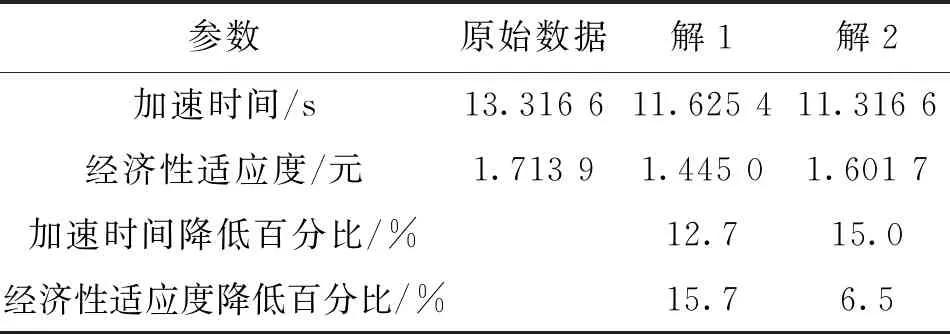
表4 優化結果對比

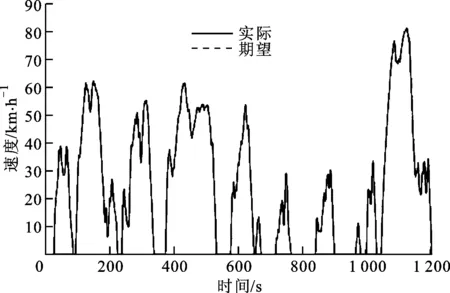
圖9 JC08工況解1速度跟蹤

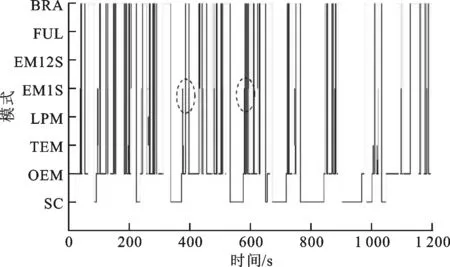
圖10 JC08工況解1模式選擇

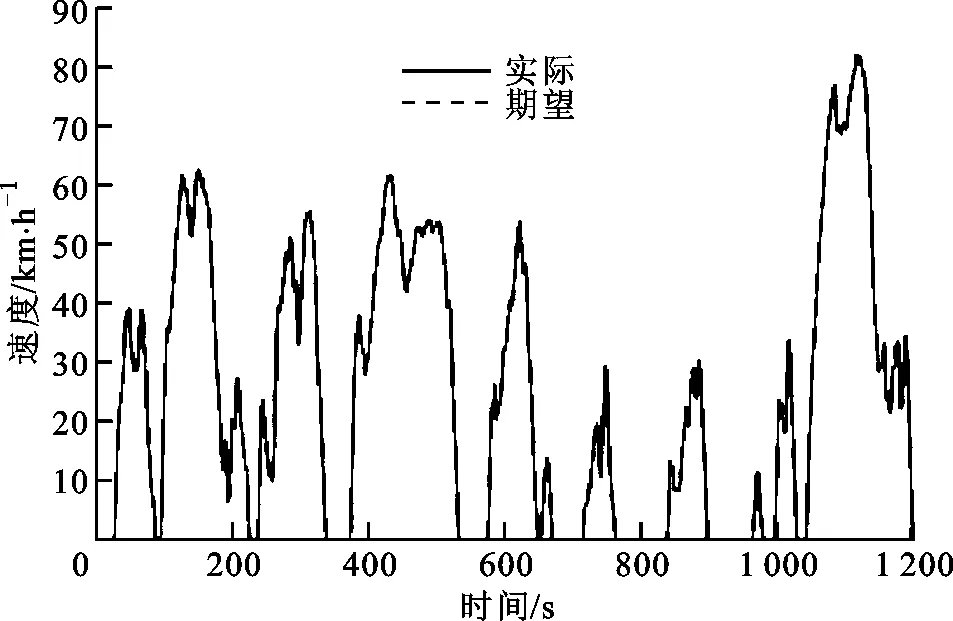
圖11 JC08工況解2速度跟蹤

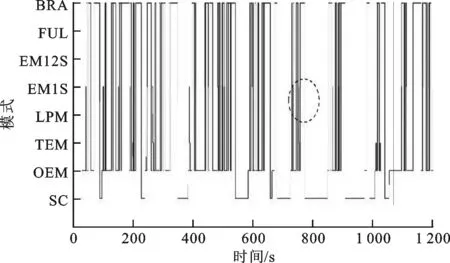
圖12 JC08工況解2模式選擇

從圖9～圖12中可以看出,JC08工況的啟停、加減速更為頻繁,循環的規律性更差,對車輛要求更高,但是在該優化參數和控制策略下仍能保證較好的速度跟蹤。從模式選擇圖可以看出,車輛的加減速頻繁,有部分文獻中指出,出于對電池壽命的考慮,不應使得電池在頻繁充電和放電之間轉換。因此,本文對所采用的制動模式進行了限制,在頻繁的低減速度下采用機械制動,為了方便表達,制動模式都放在了BRA內,故在JC08工況復雜的加減速環境下,雖然可以觀察到頻繁進入BRA,但是電機2并不會頻繁進行充放電。從圖9～圖12還可看出,控制策略均能良好跟蹤,模式基本保持穩定,虛線圓圈處表示為模式快速切換的位置,主要存在于JC08工況的冷啟動階段及高速階段,造成了速度跟蹤出現誤差,另外速度跟蹤誤差還出現在瞬態階段,其余模式選擇均正確而且穩定,證明優化結果在JC08工況下仍能較好適用。這表明額外選取區分度作為優化的適應度函數的方法具有通用性,其結果也具有一定的通用性。

5 結 論

本文根據現有的結構,參考各個動力部件的經濟區,制定了基于規則的能量管理策略,并利用Cruise和Simulink搭建了整車模型以及控制策略模型。在以經濟性和動力性為目標的基礎上,進一步提出了模式區分度的概念,定義并轉換為了第3個優化目標,以現有結構中的5個傳動比以及2個邏輯門閾值為優化參數,利用多目標粒子群算法進行優化,得到了Pareto非劣解集。選取并通過Cruise和Simulink平臺驗證了所選的3組解,其中2組解結果表明該方法能很好地降低燃油經濟性,保證動力性,同時規避了典型工作區間下頻繁模式切換的問題,車輛的穩定性和舒適性得到了提高。通過JC08這個較NEDC更為復雜的工況對所選兩組解進行了仿真驗證,結果表明,在該工況下車輛的運行穩定,并能實現速度的跟蹤,說明該優化方法具有良好的通用性。