煤礦巷道直墻半圓拱形波形鋼腹板支架穩定承載性能

吳麗麗，邱芳緣，王振偉，孫廣強

(1.中國礦業大學(北京) 力學與建筑工程學院，北京 100083; 2.煤炭科學技術研究院有限公司 安全分院，北京 100013; 3.煤炭科學研究總院 煤炭資源高效開采與潔凈利用國家重點實驗室，北京 100013)

多年來隨著開采規模和開采深度的不斷增加，使得賦存優越的煤層不斷減少，軟巖礦井數目不斷增大[1],導致軟巖支護問題越發嚴重。國內外專家學者對軟巖的支護方面做了許多試驗和理論研究，逐漸形成了錨噴、錨網噴、外錨內砌、外錨內架以及拱形金屬支架和鋼筋混凝土聯合支護、注漿加固等一系列技術[2]。金屬支架結構整體具有較高的承載能力，且其施工簡便，綜合成本低，因此在煤礦礦井中金屬支架使用較為普遍且發展的也較為迅速。

國內外巷道金屬支架主要采用礦用工字鋼或U型鋼。礦用工字鋼是礦山巷道支護設計的專用型鋼，它與普通工字鋼不同，其斷面的高寬比小，腹板厚度大，翼緣厚且斜度大，其抗彎能力強，穩定性好。但由于礦用工字鋼的可縮性差，有時不能適應軟弱圍巖變形情況。U型鋼具有良好的斷面形狀和幾何參數，使型鋼搭接后易于收縮，但由于其支護反力有限，有時難以滿足支護要求。

波形腹板工形構件是在工字鋼中用直接冷軋成形的波形腹板代替平腹板，并與平翼緣通過高頻連續焊接形成的一種新型高效型材[3]。迄今為止，國內外許多學者對波形腹板工型構件的抗剪性能、抗彎性能、抗扭性能進行了一系列的理論和試驗研究，BERGMANN和REISSNER等[4-5]通過假定邊界條件和采用正交異性板的方法，得出了單位長度的剪切屈曲荷載公式。瑞典的LUO R和EDLUND B等[6-8]采用非線性有限元進行了一系列的參數分析，分析結果表明，腹板的屈曲強度伴隨腹板厚度的增長而變大，并隨著腹板的寬度變小而變大。李時等[9]通過理論計算，考慮了幾何初始缺陷和大變形，得出了波形鋼腹板較一般構件有更強的抗剪能力。METWALLY E L等[10]通過與實際橋梁相同截面尺寸的波形腹板梁進行了試驗研究并結合限元計算方法，發現梁中的彎矩和剪力相互獨立且二者無直接關系，可忽略腹板對抗彎性能的貢獻。吳文清等[11]對試驗模型開展了試驗測試和有限元分析，得到了波折腹板梁在承受彎矩時，腹板上的應力僅在非常接近翼緣的部分有正應力而其余部分則為零。任紅偉[12]考慮了波形腹板組合簡支梁橋截面曲率的影響，并以連接構件的荷載滑移應變為基礎，推導出了附近彎矩的公式。LINDER[13]通過對波形腹板鋼梁的抗扭性能開展了試驗研究，結論表明波形腹板梁和平腹板梁相比抗扭模量基本沒有改變而翹曲常數變化較為明顯，并在試驗研究的基礎上推導出了其計算公式。上平謙二等[14-15]采用數值模擬分析方法，通過對相同截面形式的波形腹板組合梁進行了研究，提出了抗扭剛度的半經驗公式，并繪制了扭轉角和應變之間的關系曲線。郭彥林等[16-20]對波形腹板工形構件的平面外穩定、抗剪承載力、抗扭性能等進行了系統的數值模擬和試驗研究,且根據研究成果編制成《波浪腹板鋼結構應用技術規程》CECS290:2011[21]。

因此，波形腹板工形構件被許多國家應用于鋼結構屋面梁[22]和混凝土箱梁橋[23]，大跨度抗彎構件以及廠房住宅建筑[24]等。

結合波形腹板工形構件良好的性能，本課題組[25]提出了一種更適用于煤礦軟巖巷道的新型支護結構—波形腹板工形金屬支架結構，簡稱為“波形鋼腹板支架”。波形鋼腹板支架是一種將波形腹板工形構件彎制成弧形，運至施工現場，采用半剛性節點或者可縮性節點拼接各個弧段而形成的金屬支架結構。波形鋼腹板支架作為一種新型結構具有加工制作簡單，安裝、運輸方便，且具有較高的抗剪承載力，同時由于腹板波折類似“手風琴”易軸向變形而能夠適應巷道大變形等優點，可提高承載力和綜合經濟效益，有望在軟巖巷道支護中得到應用和推廣。

目前本課題對波形鋼腹板支架完成了一些研究工作:

對波形鋼腹板支架結構的截面形式進行比選以及對4種常見的截面形式(馬蹄形斷面、圓形、直墻半圓拱加反底拱、三心拱加反底拱)支架在圍巖壓力下的受力進行分析，確立了支架結構的簡化力學計算模型[26]。

通過對波形腹板工型構件、U型鋼和礦用工字鋼構件穩定承載力的比較表明，波形腹板構件的軸壓穩定承載力較高，用鋼量較省，具有良好的經濟效益[27]。

針對波形腹板工形構件的截面尺寸各參數、斷面形式對其穩定承載力的影響，討論了波幅f，波長λ，腹板高度hw，腹板厚度tw，翼緣寬度bf和翼緣厚度tf對承載力敏感程度[28]。設計了一榀馬蹄形斷面的支架，通過試驗，驗證了有限元的正確性[29]。

提出2種適用于軟巖支護的新型波形鋼腹板可縮性節點構造，并設計了7個可縮性節點試驗構件。主要涉及2種類型，分別為螺栓連接的可縮性節點和套筒楔子連接的可縮性節點，在總結試驗研究結果的基礎上提出了關于波形鋼腹板可縮性節點的初步設計步驟和改進建議[30]。

根據前期的研究結果，設計了直墻半圓拱形構件的試驗模型，測試了該支架的承載力與變形規律，并結合有限元方法對比分析。在此基礎上，對支架進行了平面內彈性及彈塑性屈曲性能的參數分析，討論截面參數、斷面半徑等對支架屈曲承載力性能的影響，進一步得到截面幾何參數對支架穩定承載力影響的一般規律。與此同時，運用有限元方法，對比了波形鋼腹板與礦用工字鋼支架在用鋼量基本相同前提下的穩定承載性能和不同應力狀態下的支護性能。

1 直墻半圓拱形波形鋼腹板支架模型試驗

筆者設計了兩榀直墻半圓拱形波形鋼腹板支架模型試件，試件編號為ZQ-1和ZQ-2，其中ZQ-2試件除翼緣厚度與ZQ-1試件不同外，其余參數完全相同。為了研究直墻半圓拱形波形鋼腹板支架的承載力、剛度和變形情況，建立了試驗支架的有限元模型，將兩者結果進行了對比，并同時分析了波形腹板翼緣厚度變化對波形鋼腹板支架承載能力的影響程度。

1.1 試件設計和材料性能

1.1.1試件設計

設計了兩榀直墻半圓拱形鋼波形腹板支架，支架由頂部半圓弧段、左直腿段和右直腿段組成，頂部半圓弧段通過節點板和高強度螺栓與直腿段連接。波形腹板工形構件的構成如圖1所示[3]。圖1中，l為構件長度；bt為1/2翼緣寬度。試驗支架拼接節點1-1采用高強度螺栓端板，拼接形式如圖2(a)所示，節點3-3是先將支架直腿段與端板焊接，再將端板固定于加載支架上，如圖2(b)所示。支架試件尺寸設計如圖3所示。支架寬5 200 mm、高4 250 mm，波形鋼腹板支架截面參數見表1，波形腹板波幅f為20 mm，波長λ為150 mm。

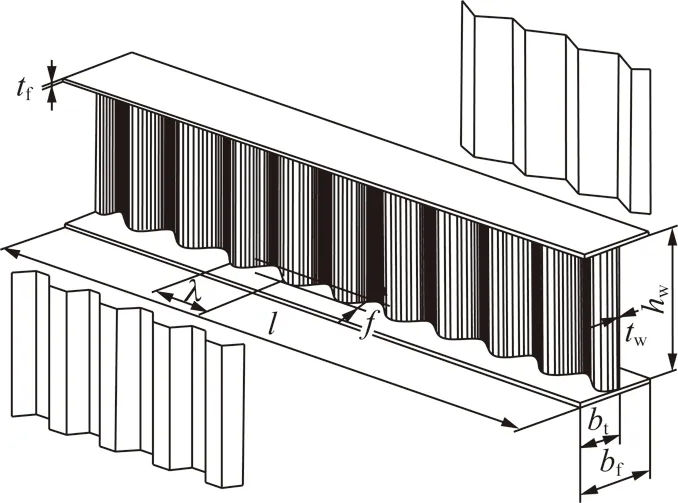
圖1 波形腹板工形構件的構成Fig.1 Composition of H-shaped members with corrugated web

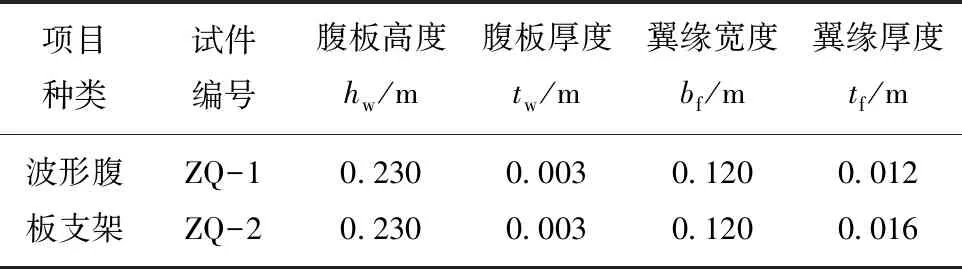
表1 構件截面參數Table 1 Cross-sectional parameters of the specimen

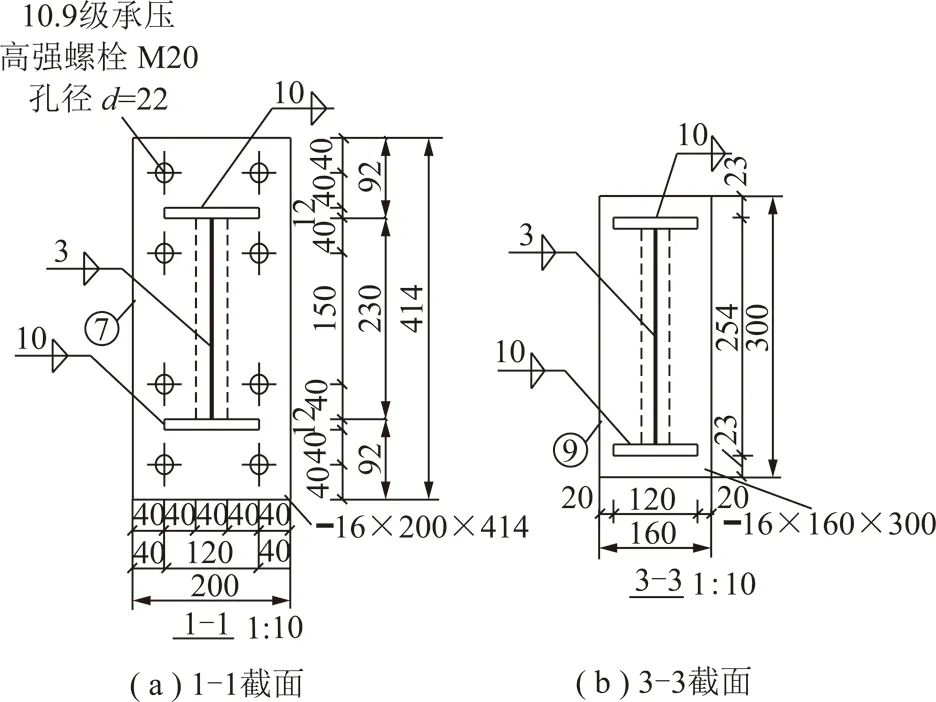
圖2 支架試件接頭結構Fig.2 Joint configuration of support model

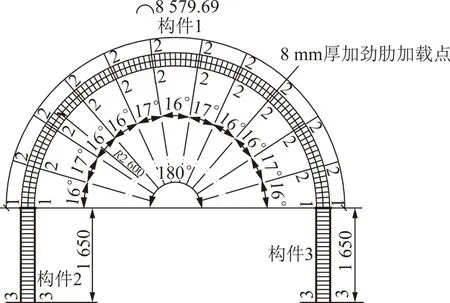
圖3 支架試件設計示意Fig.3 Diagram of section of support model

1.1.2材料性能

直墻半圓拱形波形鋼腹板支架試件中均選用Q235型號鋼材，進行金屬拉伸試驗測試鋼材型號以及性能，每種厚度鋼板各加工3塊材性試樣。經試驗測試翼緣屈服強度平均值為260 MPa，抗拉強度為420 MPa，斷后伸長率為30%;腹板屈服強度平均值為250 MPa，抗拉強度為425 MPa，斷后伸長率為30%。

1.2 加載方案及測點布置

1.2.1加載方案及試驗裝置

直墻半圓拱形波形鋼腹板支架試驗是在中國礦業大學煤炭資源與安全開采國家重點實驗室進行，采用臥式巷道支架試驗臺。為合理的模擬波形鋼腹板支架在煤礦巷道中的受力狀態，在支架上半圓弧段采用十點均布加載(即近似靜水壓力均布加載模式)。為防止支架在受力時水平面內出現面外失穩，在支架的兩個肩部和左右兩側直腿段處設置面外防護裝置。支架的加載裝置如圖4所示。試驗采取靜力單調逐級加載的方式。通過有限元數值模擬分析的方法計算ZQ-1和ZQ-2波形鋼腹板支架的極限荷載，預計極限荷載值分別為1 266.9 kN和1 636.27 kN。在達到預計極限荷載值60%之前，加載量級為20 kN/級，在預計荷載值60%～80%時，加載量級減少為10 kN/級，超過預計荷載值90%之后緩慢連續加載，加載量級減為3～5 kN/級，每級荷載的持續加載時間為2～3 min，待試件充分變形趨于穩定后，記錄測試數據，再進行下一級加載，直到支架承載能力達到最大值，且開始下降時停止加載。

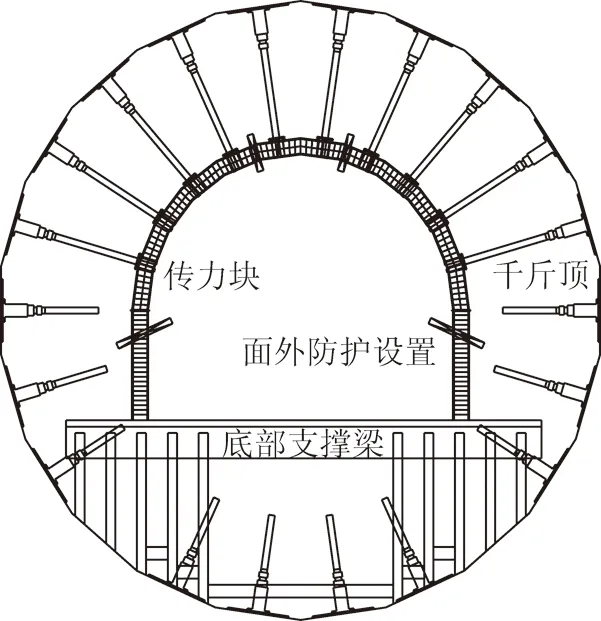
圖4 加載裝置Fig.4 Diagram of test setup

1.2.2測點布置

波形鋼腹板支架的應變片和位移傳感器測點布置如圖5所示。試驗步驟為:先將波形鋼腹板支架在地面組裝好，再放樣對中找出半圓弧的中心位置，吊裝支架到試驗平臺，安裝面外防護裝置，畫出對應應變片的位置，打磨并粘貼應變片，安裝位移傳感器，并連接好相應電線，一切準備就緒并觀察試驗平臺周圍確保無危險物品后再開始試驗。

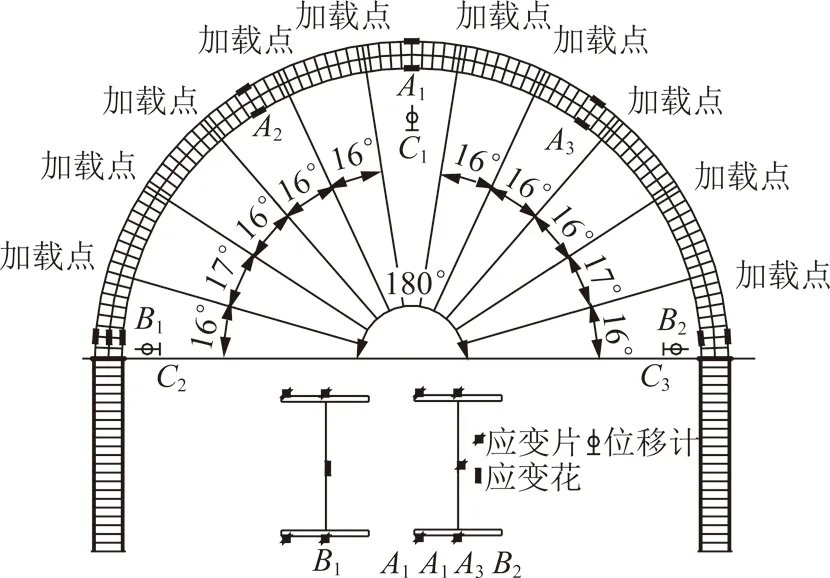
圖5 測點布置Fig.5 Layout of measuring points

1.3 試驗結果及分析

1.3.1荷載-位移曲線

(1)ZQ-1試件結果:根據試驗監測到的波形鋼腹板支架的荷載和位移數據，以所有主動荷載的標量和為縱坐標，分別以支架頂部半圓弧段頂部中心位置的豎向位移d1、頂部半圓弧段與左側直腿段相連接處的水平位移d2及頂部半圓弧段與右側直腿段相連接處的水平位移d3為橫坐標繪制荷載-位移曲線，如圖6所示。支架破壞時為整體非對稱變形，未發生局部失穩，頂部弧段壓平，右側直腿與半圓弧連接處水平位移最大。受場地和試件的影響，試驗試件存在初始幾何缺陷，加載千斤頂在運行中也不能實現同步十點均布加載，支架幾何非線性效益增大，故它的平衡路線會過早偏離線彈性路線，發生平面內的彈塑性非對稱失穩破壞(由于各種缺陷如幾何缺陷，殘余應力，加載不能同步等原因造成支架出現了左右兩側位移不等，故本文稱為“非對稱失穩”)。

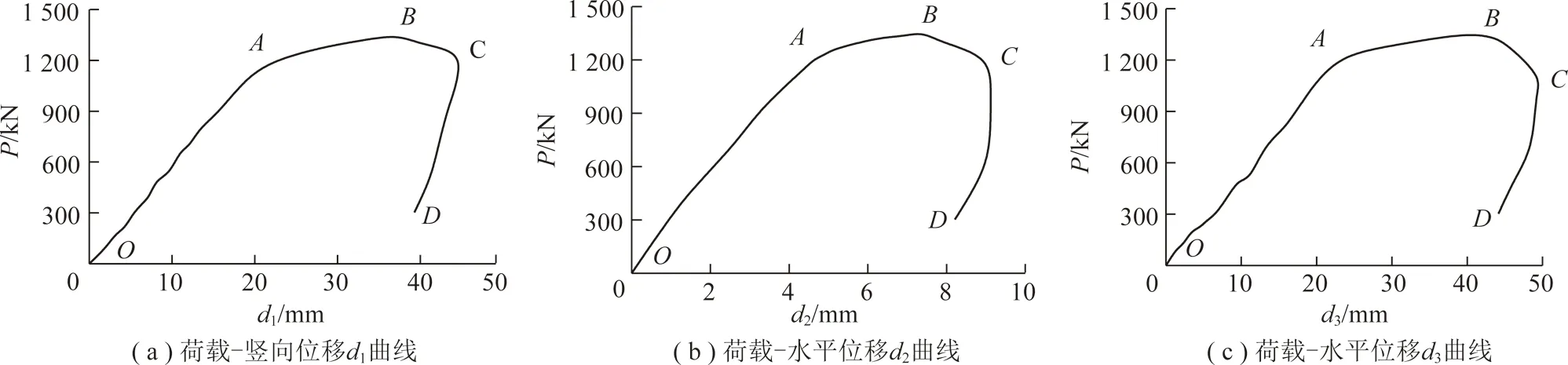
圖6 ZQ-1試件荷載-位移曲線Fig.6 Load-displacement curves of ZQ-1 specimen

由圖6可知，ZQ-1試件的荷載-位移曲線可以分成OA，AB，BC和CD四個階段，不同階段的具體變化特征:OA段即近似彈性階段，這一階段隨著荷載的增加位移持續增長，支架左右水平側位移相差逐漸增大，以右側水平位移為主，支架整體處于穩定階段;AB段即近似彈塑性階段，這一階段位移增長較快而荷載上升緩慢，支架頂部半圓弧段被壓平，右側水平位移持續增大，支架向右傾斜進入失穩階段;BC段即失穩破壞階段，曲線下降，這一階段荷載不斷下降;CD段即卸載段，卸載后支架整體有位移恢復現象。支架試驗前后對比如圖7所示。

(2)ZQ-2試件結果與分析:ZQ-2試件與ZQ-1試件使用同一加載設備，加載方式與約束條件完全相同，僅改變了波形鋼腹板翼緣的厚度。支架最終破壞形式同為整體非對稱失穩變形，且未發生局部失穩，根據實際監測到的波形鋼腹板支架荷載與位移數據，分別繪制荷載-位移曲線如圖8所示。支架變形也可分為4個階段，各階段的變化特征與ZQ-1相似。

圖7 ZQ-1試件試驗前后對比Fig.7 Diagram of before and after test of the ZQ-1 specimen

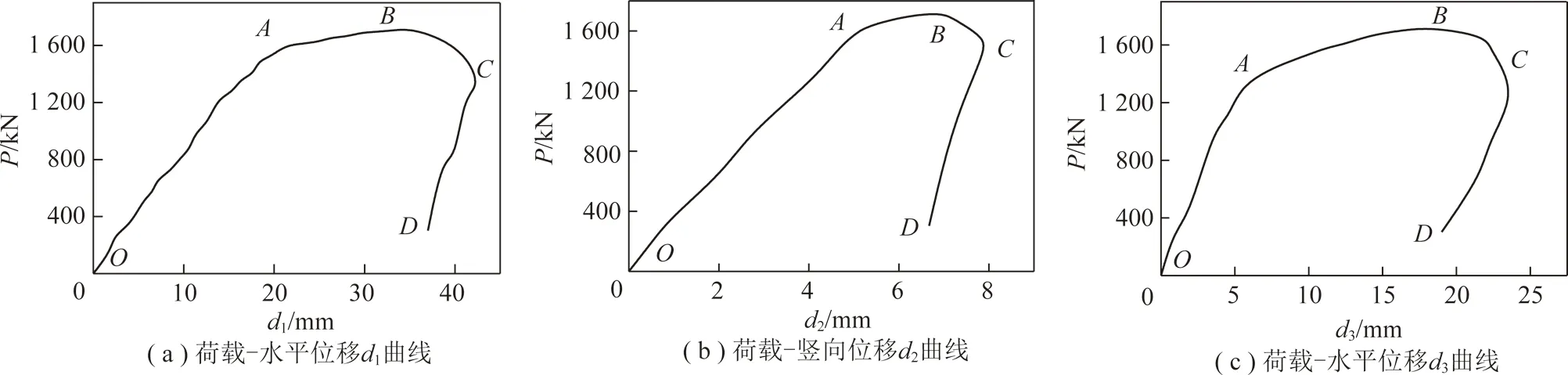
圖8 ZQ-2試件荷載—位移曲線Fig.8 Load-displacement curve of ZQ-2 specimen

1.3.2穩定承載力對比

支架試驗ZQ-1和ZQ-2均為非對稱失穩見表2，ZQ-2試件相比ZQ-1試件翼緣厚度由12 mm增為16 mm，增幅為33%，相應承載力由1 352.6 kN提高至1 722.9 kN，提高了27.38%;拱頂豎向位移由32.25 mm增加至35.26 mm，提高了10.39%;支架的單位承載力由3.29 kN/kg提高至3.43 kN/kg，提高了4.26%。這說明翼緣厚度對支架的承載性能有顯著影響。

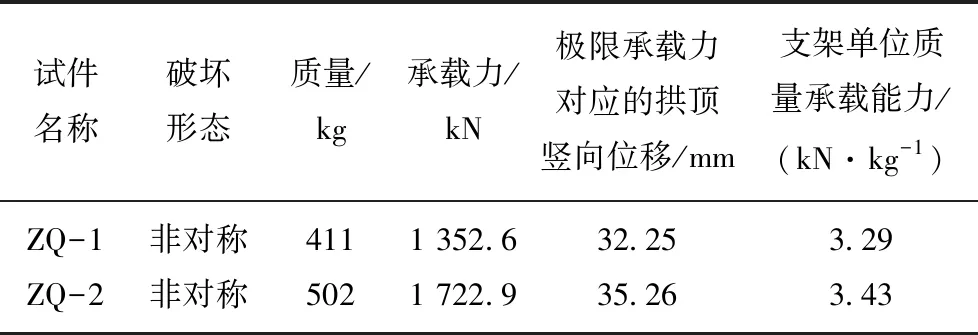
表2 波形鋼腹板支架試驗對比Table 2 Comparison of experiment results of support with corrugated webs

2 試驗與有限元計算結果的對比

采用ANSYS建立上述試驗ZQ-1試件的有限元模型，采用與試驗相同的截面參數、加載方式和約束條件，分析波形鋼腹板支架的穩定承載性能，并與試驗結果進行對比。

2.1 試驗結果與計算結果的對比

支架的斷面尺寸及截面參數均與試驗ZQ-1試件相同，支架的翼緣和腹板都采用SHELL181單元。假設鋼材為理想彈塑性材料，其彈性模量Es=206 GPa，泊松比為ν=0.3，屈服強度采用鋼材材性試驗的實測值fy=262 MPa。試驗支架弧形段的拼接節點1-1采用高強度螺栓端板連接，視為剛性連接節點，因此有限元模型中直接耦合支架兩端端板截面上節點的所有自由度。對于兩直腿柱腳截面3-3，約束該截面上節點的3個方向平動自由度和轉動自由度。支架的有限元模型如圖9所示。

圖9 波形鋼腹板支架的有限元模型Fig.9 FEM model of steel support with corrugated webs

在與試驗ZQ-1試件施加相同的10個加載點，進行非線性屈曲分析，將分析結果與試驗結果進行對比，如表3和圖10所示。圖中縱坐標為10個加載點極限荷載之和，橫坐標為半圓弧段拱頂的垂向位移。根據對比可知有限元分析和試驗模型所得的極限承載力僅相差6.7%，極限承載力對應的拱頂垂向位移也僅僅相差15.71%，試驗曲線與有限元曲線較吻合，這表明有限元分析結果與試驗結果吻合較好，驗證了波形鋼腹板支架有限元模型的正確性。

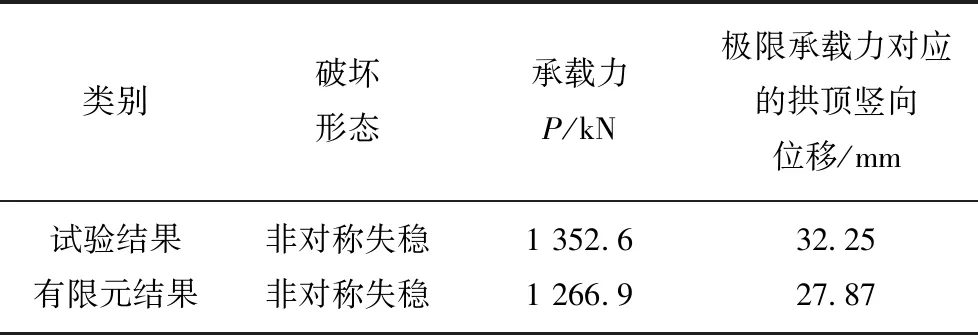
表3 波形鋼腹板支架有限元分析結果與試驗結果對比Table 3 Comparison of results between experiment and FEA

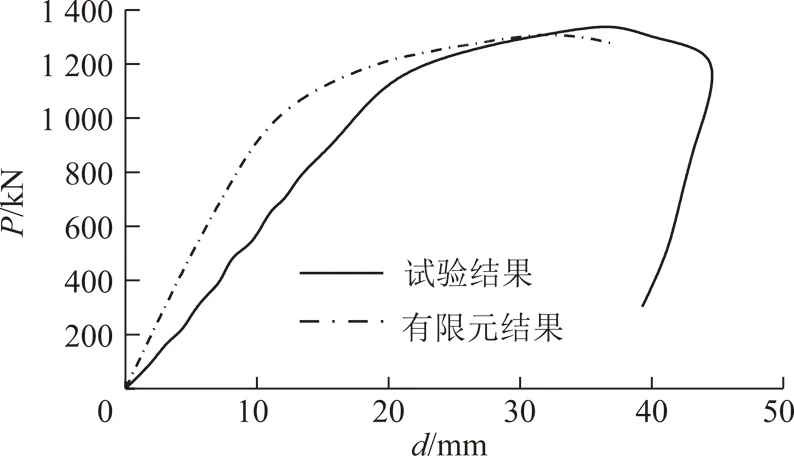
圖10 試驗與有限元分析的支架荷載-位移曲線對比Fig.10 Comparison of load-displacement curve between test and FEA

2.2 與礦用工字鋼的有限元計算結果對比

設計與ZQ-1試件用鋼量相同的礦用工字鋼支架，該支架同樣采用SHELL181單元進行有限元模擬。礦用工字鋼的斷面尺寸為:翼緣寬度95 mm，厚15 mm，總高度120 mm，腹板厚11 mm。支架達到極限狀態時承載力為1 027.2 kN，對應豎向最大位移為40.05 mm。礦用工字鋼支架的加載方式、邊界約束條件和分析方法與波形鋼腹板支架相同，將2種支架的有限元分析結果進行對比，見表4。

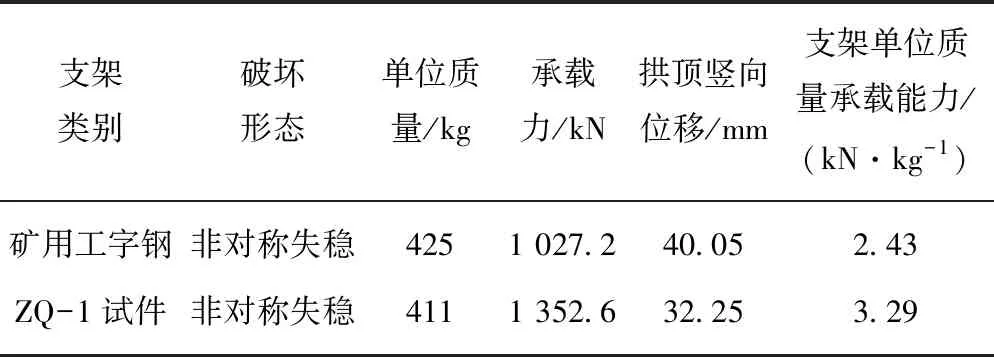
表4 ZQ-1支架與礦用工字鋼結果對比Table 4 Comparison of results between ZQ-1 supports and I-steel for mining

由表4可知，用鋼量基本相同的前提下，波形鋼腹板支架ZQ-1的承載力比礦用工字鋼提高了31.68%，其變形為礦用工字鋼的4/5左右，且波形鋼腹板支架的單位質量承載能力是礦用工字鋼支架的1.35倍，這說明波形鋼腹板支架的穩定承載性能優于礦用工字鋼支架。

3 支架穩定承載性能數值分析

采用ANSYS有限元軟件對靜水壓力作用下結構的彈性穩定(屈曲分析)，并以此為基礎進行非線性屈曲分析。同時對不同圍巖荷載作用方式下波形鋼腹板支架和礦用工字鋼支架的變形和破壞方式進行分析，進而說明波形鋼腹板支架的支護性能。

3.1 彈性屈曲分析

本文的波形鋼腹板支架由于有比較可靠的面外側向支撐，因此不考慮平面外失穩破壞形式。鑒于支架的試驗與有限元結果基本吻合，采用支架的有限元模型進行分析。對靜水壓力作用下直墻半圓拱形斷面波形鋼腹板支架進行平面內穩定分析，在進行彈塑性屈曲分析時，需添加一定的初始缺陷，此處添加的初始缺陷為彈性屈曲分析所得的一階非對稱屈曲模態的2S/500,S為封閉支架的計算孤長度。在進行彈塑性分析時，需考慮材料的非線性問題，鋼材的本構關系采用理想彈塑性材料，屈服強度fy=275 MPa，彈性模量Es=206 GPa，泊松比ν=0.3。

有限元數值分析表明，柱腳固定、施加靜水壓力的情況下，直墻半圓拱形斷面波形鋼腹板支架的一階屈曲模態為非對稱失穩，如圖11所示。

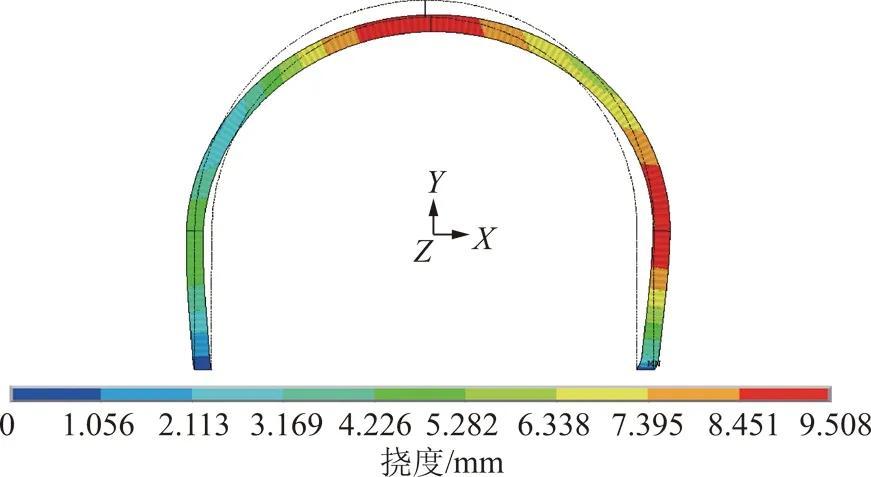
圖11 直墻半圓拱支架彈塑性非對稱失穩變形云圖Fig.11 Deformation of elastoplastic antisymmetric instability of vertical wall semicircle support

首先以試驗波形鋼腹板支架的截面尺寸為基準，對直墻半圓拱形截面形式的波形鋼腹板支架進行彈性屈曲分析，接著基于該截面尺寸，逐一變化波形鋼腹板支架截面各參數，分析截面各參數對支架彈性屈曲荷載的影響。

3.1.1屈曲模態

由圖12可知，直墻半圓拱形斷面波形鋼腹板支架的一階屈曲模態為非對稱失穩，二階為正對稱失穩屈曲模態，且二階屈曲特征值均約為一階屈曲特征值的1.69倍，說明直墻半圓拱形斷面的波形鋼腹板支架更易于發生非對稱失穩。

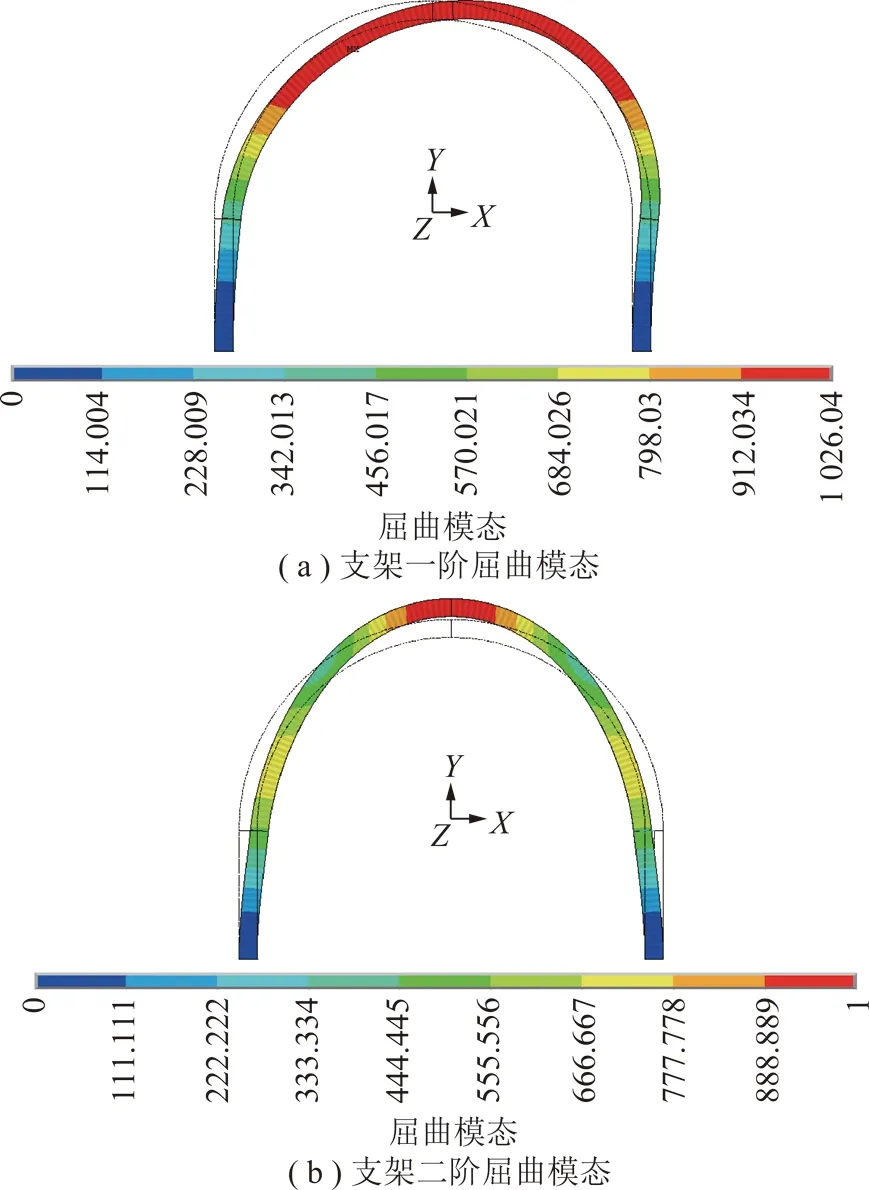
圖12 直墻半圓拱形支架彈性屈曲模態Fig.12 Eigenvalue buckling modes of vertical wall semicircle arch supports

3.1.2彈性屈曲分析

以試驗波形鋼腹板支架截面和斷面尺寸為基礎，逐一變化波形鋼腹板支架截面各參數，包括波形腹板的高度hw、波形腹板的厚度tw，翼緣的寬度bf、翼緣的厚度tf這4個參數，分析截面各參數對支架彈性屈曲荷載的影響，如圖13所示。

由圖13(a)可知，支架彈性屈曲荷載均隨著腹板高度的增加而顯著增大。由圖13(b)可知，隨著腹板厚度的增加支架彈性屈曲荷載稍有增大，基本呈線性關系。由圖13(c)可知，隨著翼緣的寬度的增加彈性屈曲荷載有所降低。由圖13(d)可知，隨著翼緣厚度的增加，彈性屈曲荷載而增大，基本呈線性增加關系。綜合以上圖13可知在靜水壓力作用下，直墻半圓拱形支架彈性屈曲荷載隨著腹板高度和翼緣厚度的增加而顯著增大，而翼緣寬度的影響較小。

3.1.3彈塑性屈曲分析

根據支架的平面內失穩破壞形式分析，支架結構在實際情況中大多數是沿著二階彈塑性曲線的路線發生非對稱失穩破壞，因此對直墻半圓拱形支架截面尺寸各個參數與平面內彈塑性穩定的關系進行研究，并對比不同斷面形式對支架各個參數的敏感程度。以試驗支架斷面尺寸為基礎，逐個變化波形鋼腹板支架的各個截面參數，主要包括波形腹板高度、腹板厚度、翼緣寬度和翼緣厚度。支架建模及約束方式均同上文，此處不再贅述。支架彈塑性穩定承載力隨各個參數的變化如圖14所示。

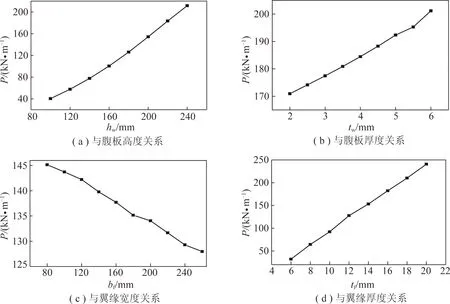
圖13 支架彈性曲荷載與截面尺寸關系Fig.13 Relation between elastic buckling loads and sectional parameters

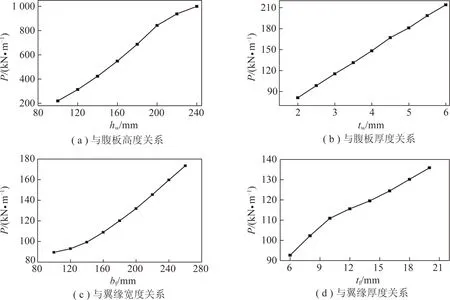
圖14 彈塑性穩定承載力與截面尺寸參數關系Fig.14 Relationship between elasto-plastic stability capacity and sectional parameters

由圖14(a)可知，隨腹板高度增加，直墻半圓拱形支架彈塑性穩定承載力變化比較顯著，基本呈線性增加關系。當腹板高度由100 mm增加至240 mm(2.4倍)時，直墻半圓拱形支架穩定承載力由219.53 kN/m增大為999.76 kN/m(4.6倍)。由圖14(b)可知，隨著腹板厚度的增加，直墻半圓拱形支架穩定承載力呈直線增加趨勢。由圖14(c)可知，隨著翼緣寬度的增加，直墻半圓拱形支架的彈塑性承載力顯著增加。由圖14(d)可知，隨著翼緣厚度的增加，直墻半圓拱形支架穩定承載力也有所增大，但增幅不及前3者。

3.2 不同荷載情況下支架數值模擬

支架受載一般分為3種情況:垂直單向受載、均勻受載和水平地應力為垂直地應力的1/2，其荷載力學模型如圖15所示。通過ANSYS數值模擬對不同圍巖荷載作用方式下波形鋼腹板支架和礦用工字鋼支架的變形和破壞方式進行分析，進而說明波形鋼腹板支架的支護性能。

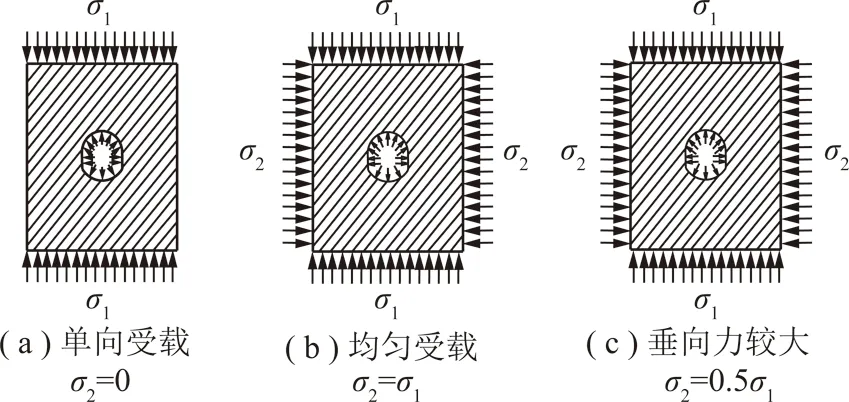
圖15 荷載力學模型Fig.15 Load mechanical model

(1)靜水壓力作用下情況

波形鋼腹板支架截面參數同試驗支架ZQ-1試件的斷面尺寸及截面參數，其用鋼量和相應斷面形式的12號礦用工字鋼支架相同。邊界條件設為模型左右兩直腿底部截面固定約束。通過模型頂部半圓弧段及兩直腿段對模型逐漸施加同步均勻荷載即壓應力，直至波形鋼腹板支架破壞為止,支架最終變形如圖16所示。

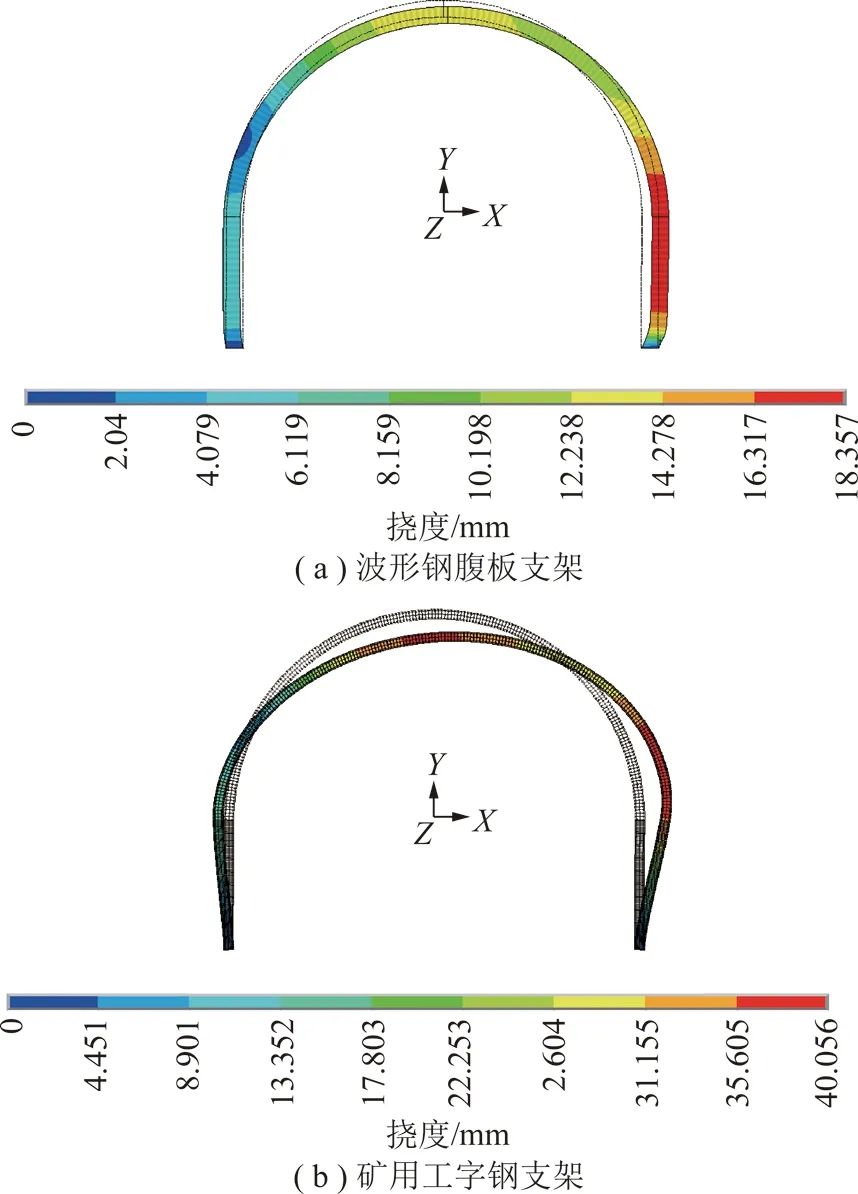
圖16 靜水壓力作用下支架變形Fig.16 Deformation diagram of two kinds of stents under hydrostatic pressure

支架頂部半圓弧段下沉量和側幫變形先是隨著靜水壓力的增加緩慢增長，當荷載超過某一數值后，變形量增長速度加快，當荷載達到極限時支架變形持續增長，但數值模擬停止運算。從圖16可以看出2種支架結構頂部半圓弧和側幫變形較大，且波形鋼腹板支架結構的頂部最大下沉量和側幫變形分別為16.2，18.3 mm，均小于礦用工字鋼支架頂部最大下沉量49.5 mm和側幫變形53.4 mm，支護效果較好。對波形鋼腹板采用Von-Mises破壞準則，支架破壞方式均為整體失穩破壞，未出現局部失穩。

(2)垂直單向應力作用下情況

計算模型垂向地應力作用明顯，在該狀態下分析2種形式支架的支架變形量和破壞方式，以研究2種形式支架的支護性能，支架最終變形如圖17所示，可以看出2種支架結構最大變形位置均在支架頂部半圓弧處，波形鋼腹板支架結構的頂部最大下沉量為9.7 mm小于礦用工字鋼支架的53.6 mm，支護效果較好。對波形鋼腹板支架采用Von-Mises破壞準則，荷載增加到一定程度時支架發生破壞，均為整體失穩。

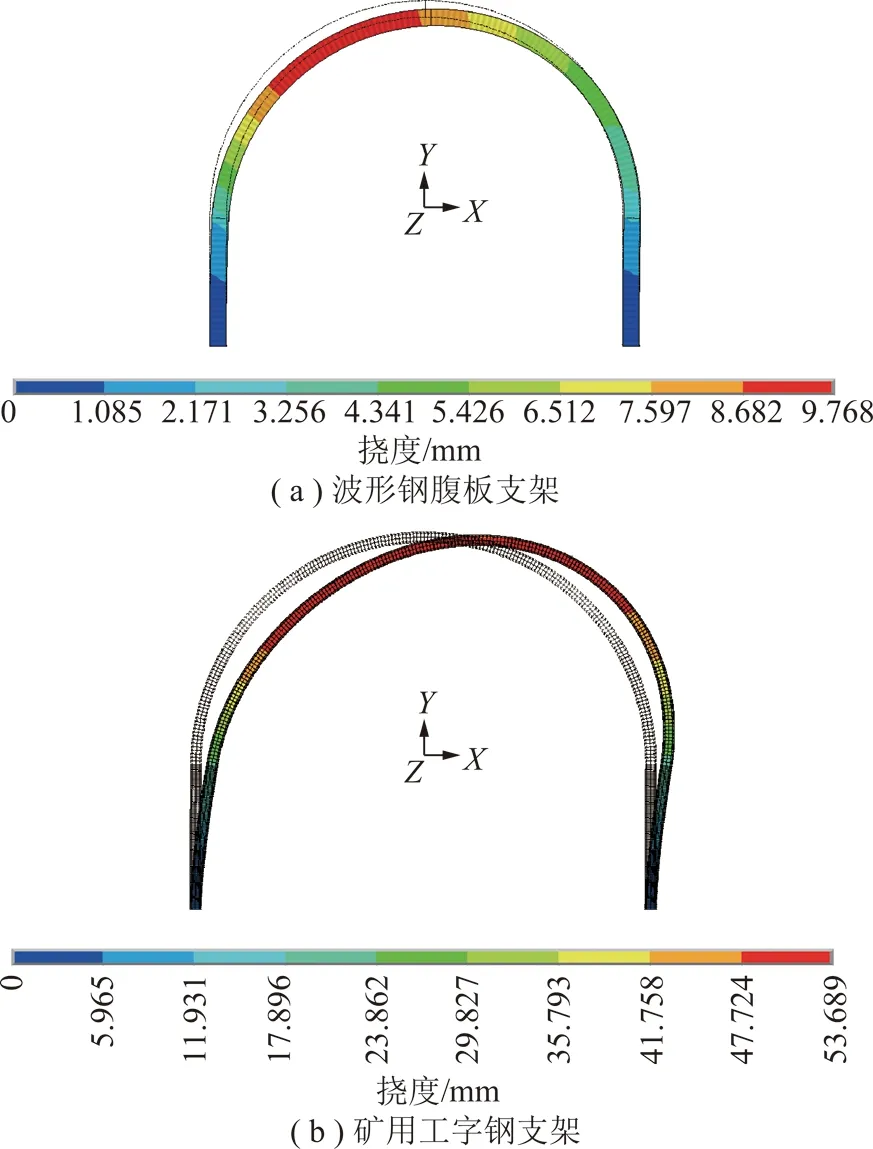
圖17 垂直單向應力作用下支架變形Fig.17 Deformation diagram of two kinds of stents under Vertical unidirectional stress

(3)垂向應力為主、側向應力小的荷載作用下支架數值模擬

計算模型水平應力為垂向應力的0.5倍，垂向地應力作用明顯，在該狀態下分析2種形式支架的變形量和破壞方式，對比2種形式支架的支護性能，支架最終變形如圖18所示。波形鋼腹板支架結構的頂部最大下沉量為8.9 mm和側幫變形為9.1 mm，均小于礦用工字鋼支架頂部最大下沉量36.7 mm和側幫變形56.2 mm。可以看出波形鋼腹板支架的變形量約為礦用工字鋼的1/4，表明波形鋼腹板支架支護性能較好。對波形鋼腹板支架采用Von-Mises破壞準則，荷載增加到一定程度時支架發生破壞，均為整體失穩，未出現局部失穩。

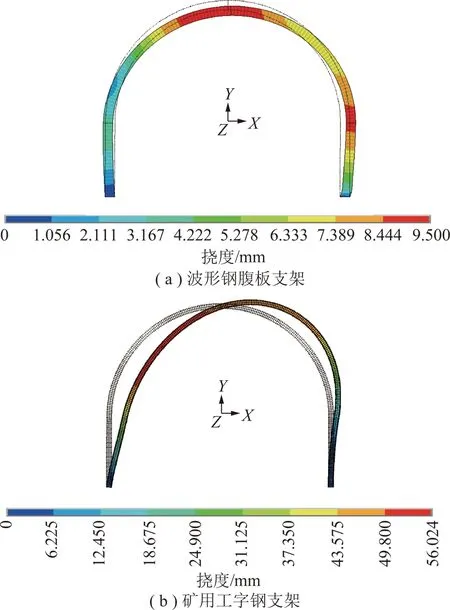
圖18 垂向力為主的荷載作用下支架變形Fig.18 Deformation diagram of two kinds of stents under the action of vertical force

4 結 論

(1)支架最終破壞形式為整體非對稱失穩，半圓弧頂部被壓平，支架右側直腿水平位移明顯。對于直墻半圓拱形波形鋼腹板支架，翼緣厚度由12 mm增至16 mm時，其極限承載力提高約27.38%，表明翼緣厚度對該類型支架的承載性能有顯著影響。在模型試驗的基礎上，對試驗支架進行了非線性屈曲分析，分析結果與試驗結果基本吻合，驗證了波形鋼腹板支架有限元模型的正確性。

(2)波形鋼腹板支架承載性能明顯優于礦用工字鋼支架。采用有限元方法對用鋼量基本相同的礦用工字鋼支架和波形鋼腹板支架進行對比，結果表明:波形鋼腹板支架比礦用工字鋼支架的承載力提高了31.68%，其變形僅為礦用工字鋼的4/5。

(3)采用有限元方法研究直墻半圓拱形斷面支架的彈塑性穩定承載力對截面各參數的敏感程度，結果表明:對于直墻半圓拱形鋼波形腹板支架，腹板高度hw和腹板厚度tw對彈塑性穩定承載力影響較大，是其敏感參數。

(4)通過數值模擬比較了波形鋼腹板支架和礦用工字鋼支架分別在不同應力狀態下的支護性能，發現波形鋼腹板支架在各種荷載狀態下的變形量均小于礦用工字鋼支架，支護效果優于礦用工字鋼支架。在承受圍巖壓力下的穩定性能良好，由于其腹板類似“手風琴”因而能適應軟巖的大變形，從而產生軸向變形，大大改善了結構的施工和使用性能，能明顯提高結構的綜合效益。