基于改進粒子群算法V型非傳統布局倉庫通道優化設計

劉建勝， 熊 峰, 胡穎聰

(1.南昌大學 機電工程學院，江西 南昌 330031; 2.南昌大學 經濟管理學院，江西 南昌 330031)

0 引言

隨著德國“工業4.0”項目計劃，我國智能制造2025計劃的相繼提出，智能工廠、智能生產、智能物流以及整個生產制造供應鏈的智能化已成為理論研究和科研實踐熱點。倉儲管理環節由原來不受重視的作業性、輔助性角色,上升為企業策略運作的重要環節及能為企業取得競爭優勢、降低成本的利潤源泉。長期以來，國內外大多數學者主要針對傳統倉庫布局方式開展研究，但是2009年美國學者Gue和Meller[1]提出了非傳統布局方式，通過分解各類倉庫業務操作成本，發現在一定的假設下，相比傳統倉庫布局模式，非傳統型倉儲布局方式能夠減少平均約10%～20%左右的移動距離。非傳統型的倉儲布局方式在分揀路徑優化方面表現出了優勢，激發了科研人員對倉儲布局設計優化的重新思考和放松假設條件的研究興趣。倉庫優化設計主要包含了三個方面的問題，一是布局設計，二是貨位分配，三是路徑優化[2]。國內蔣美仙等從角度建模和移動距離建模兩個方面研究了基于fishbone的倉庫布局優化設計[3]。S.S.Rao和G.K.Adil提出根據貨物的需求將貨物分成A、B、C三個等級，需求越大的貨物所分配的存儲貨位離存取點越近[4]。目前國內外對非傳統布局優化設計研究的成果不多，并且現有研究主要針對布局設計、貨位分配及路徑優化等內容的獨立研究，沒有結合研究。實際工作過程中，布局設計、貨位分配及路徑優化是業務上是相互聯系，互相影響。本文針對非傳統Flying-V新型倉庫布局，每條揀貨通道存取作業的概率也不同的現狀，結合物動量ABC分類法進行概率分配的非完全隨機策略，在此基礎上進行主通道的設計，優化倉庫平均揀貨距離，并用實例驗證算法有效性。

1 倉庫布局設計

1.1 倉庫布局

國內配送中心大多屬于勞動密集型產業，而且現代的倉儲自動化系統需要很高的成本，對于國內大多數配送中心尤其是配送量不大的配送中心來說，依靠廉價的人力成本的傳統型倉儲仍是較好的選擇。如圖1所示，是傳統的雙分區型倉庫布局方式，倉庫的設計一般都滿足一些設計的規則：揀貨通道之間相互平行且與主通道垂直，基于傳統布局結構性質，一般傳統型布局倉庫運作效率不高。在倉庫設計時，倉庫面積利用率和平均揀貨距離往往是兩個互相矛盾的優化目標，傳統倉庫布局通道少，倉庫的面積利用率高，揀貨效率下降。從倉庫主體作業流程分析，倉庫作業時間的60%是分揀配貨過程[5]，盲目的增加揀貨通道數量來提高效率的需求在實際倉庫管理中也是不可取的，因此合理的設計倉庫的通道和結構，使得在盡可能保證倉庫面積利用率的情況下提高貨物存取的效率是非常有必要的。

如圖2所示是非傳統Flying-V型倉庫布局，Flying-V型倉庫布局打破了傳統倉庫設計的規則，對傳統型布局中的主通道重新進行設計，由倉庫存取點引伸出兩條斜向的主通道，再由主通道進入到各條揀貨通道，主通道與貨架成了一定的角度，并且主通道也不是直線。當倉庫的規模相同時，這種倉庫布局相對于傳統型的倉庫布局能明顯減少平均揀貨距離，有效提高運作效率。

圖1 雙分區型布局

圖2 Flying-V型布局

1.2 非傳統V型布局設計

1.2.1 符號說明

Gue提出的Flying-V型倉庫布局針對單元式貨架倉庫，基于倉庫只有一個P&D點，假設每條通道具有連續并且相同的揀貨作業，即人工去到每個貨位點的概率是相等的[6]。但是實際的倉庫使用中，尤其是人工揀貨倉庫，因為存儲的貨物種類、出入庫頻率等差異，如果使用隨機的存儲策略，無疑會增加倉庫使用的成本。所以結合基于貨物周轉率的存儲策略來設計Flying-V型布局，相關參數說明如下：

P&D：存取貨物的入口；w：揀貨通道和主通道寬度的1/2；a：揀貨通道之間的水平距離；h：倉庫的寬度；bi：第i條揀貨通道在V型通道口的縱向距離(縱深值)，即y軸上的長度取值；qi：第i條揀貨通道中對應的自P&D點經底部橫向通道和經V型主通道到該點的距離相等的點，qi為該點到底部橫向通道的縱向距離，即對應y軸上的長度取值；Di：第i-1條揀貨通道和第i條揀貨通道之間的V型主通道的長度；y：貨位到倉庫底部的距離。

1.2.2 Flying-V型布局建模

如圖3所示，在單元式貨架倉庫中倉庫通道由豎直的揀貨通道、V型主通道和底部橫向通道組成，在模型中，V型主通道看成是由多個離散的點連接而成，每一條揀貨通道分別對應一個點，模型的優化目標是倉庫的平均揀貨距離最短。

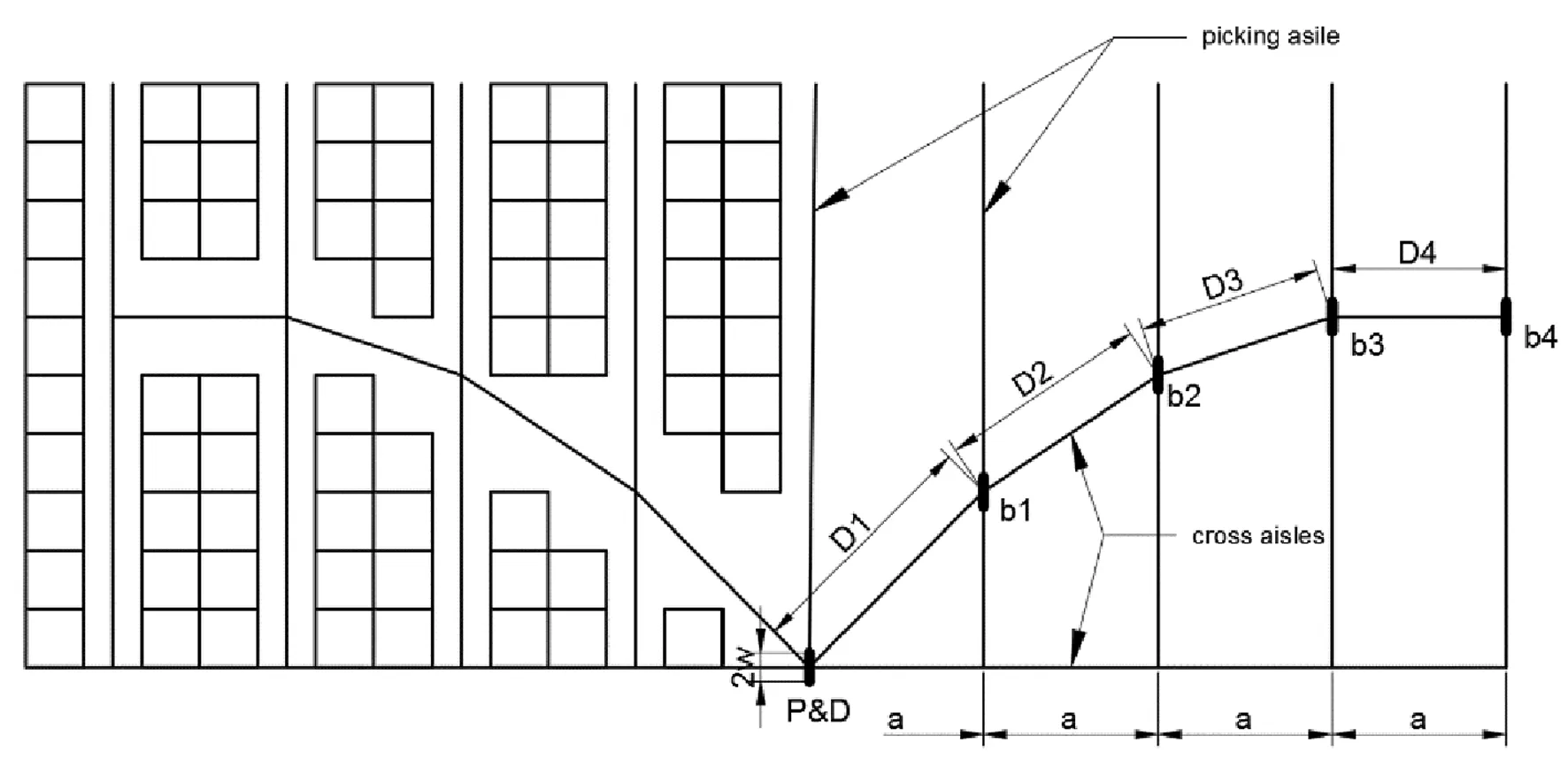
圖3 Flying-V型倉庫布局建模

假設通道的寬度均為2w，插入主通道會使得倉庫的存儲空間減少。考慮到主通道與揀貨通道并不是垂直的，所以主通道的寬度會小于2w，忽略這個因素的影響。由于倉庫的布局是對稱的，所以只需要對倉庫的半側進行建模分析。假設倉庫的一邊有n+1條揀貨通道(包括中間的通道0)，則根據勾股定理，相鄰揀貨通道i-1和揀貨通道i之間的主通道的長度Di為：

(1)

bi并不一定大于bi-1,所以模型能夠考慮到主通道所有可能的位置。對于每一條揀貨通道i，都有一個臨界點qi，使得從底部主通道經揀貨通道到該點的行走距離和從V型主通道經揀貨通道到該點的行走距離相等，即：

(2)

可以得到：

(3)

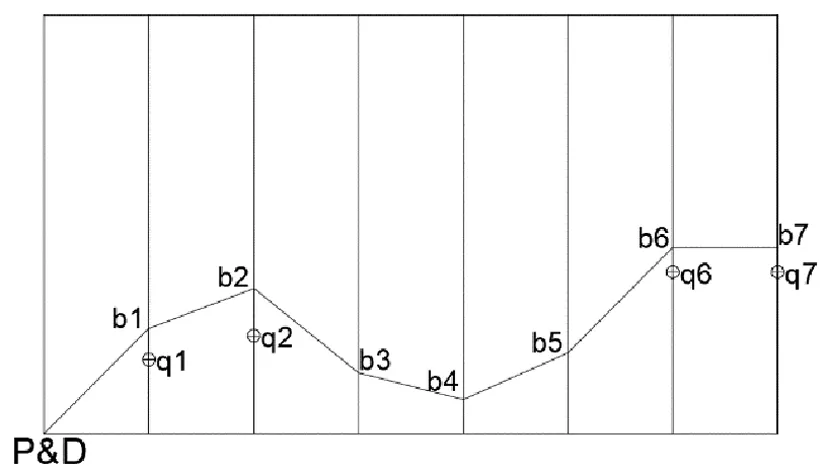
圖4 V型通道優化模型

不同貨位的揀貨距離是不同的，qi與bi并不是相互獨立的，qi的值隨著bi的值變化，qi可以簡化揀貨距離公式。用Di(y,b)來表示揀取第i條揀貨通道內距離底部橫向通道距離為y的貨位上貨物時揀貨距離。

如圖4中所示通道1、2、6、7所示，當通道i上存在滿足條件的qi時，對于i≥1的揀貨通道，揀貨距離Di(y,b)如下：

(4)

如圖4中的通道3、4、5所示，當通道i上不存在滿足條件的qi時，對于i≥1的揀貨通道，揀貨距離Di(y,b)如下：

Di(y,b)=ia+y

(5)

則對于i≥1的揀貨通道，對不同位置的貨物揀取時要選擇主通道使得揀貨距離最短，當通道i上存在滿足條件的qi時，則該揀貨通道的平均揀貨距離如下：

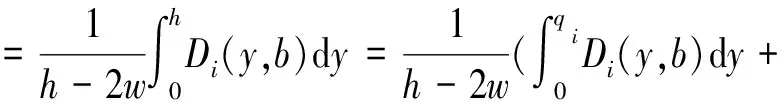
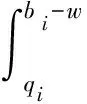
(6)

當通道i上不存在滿足條件的qi時，通道i對應的平均揀貨距離為：

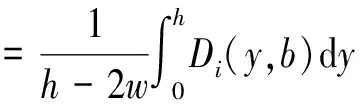
(7)

在通道0揀貨時不用考慮橫向的選擇，所以通道0的平均揀貨距離如下：

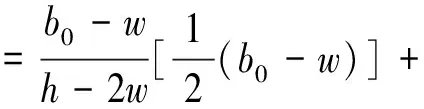
(8)

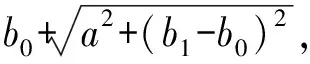
即平均揀貨距離會比b0>0時小，所以當通道的寬度為2w時，b0的最優解為w。

則當考慮隨機存儲策略時倉庫總的平均揀貨距離為：

(9)

此時的目標函數如下：

(10)

1.2.3 物動量ABC貨位分配策略

在倉庫布局設計時，可以結合對倉庫的EIQ定量分析[7,8]，倉庫訂單信息中的E(訂單件數：OrderEntry)、I(貨品種類：Item)、Q(數量：Quantity)是物流特性中的關鍵因素，所以可以通過對這三個物流關鍵因素進行分析，從而選擇合適的物流作業方式和布局, 田歆[9]具體分析了ABC管理的庫存控制、訂貨補充、儲位分配等應用策略的整體作用、改善程度以及策略之間的影響，推導出ABC管理后分揀配貨作業效率提高率的公式，從定量的角度驗證了EIQ-ABC分析法能夠大幅改善分揀配貨的效率。

考慮到倉庫的布局主要的影響因素是貨物的物動量大小，所以主要對倉庫數據進行品項數量(IQ)分析，即了解各類產品出貨量的分布狀況，分析出貨商品品項與出貨量的關系。用E1、E2、E3、…、Ei表示一段時間內倉庫處理某種貨物的訂單，用I1、I2、I3、…、Ii表示貨物品種，用Q1、Q2、Q3、…、Qi表示對應貨物周轉量。則貨物物動量分析表如下：

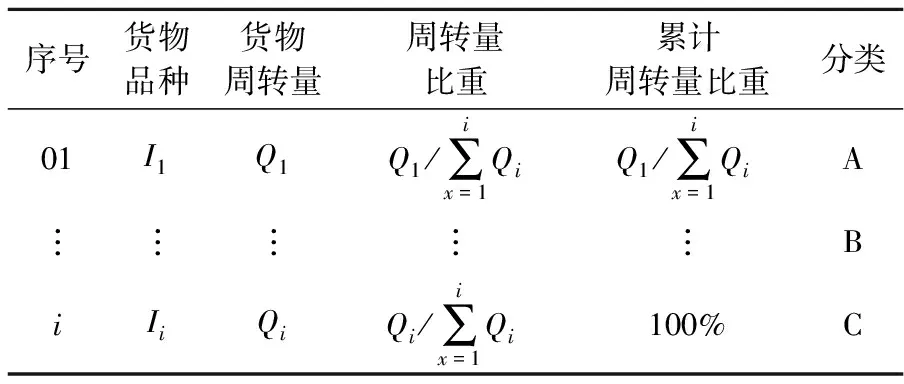
表1 物動量ABC分析表

如表1中所示，按照貨物周轉量Qi由大到小的順序進行，并計算周轉量比重和累計周轉量比重，可以將累計周轉量百分比在60%～80%的定義為A類貨物，將累計周轉量百分比在20%～30%的定義為B類貨物，其余定義為C類貨物。

為了優化倉庫結構，增強倉庫的運作效率，可以根據貨物的ABC分類結果對倉庫貨架進行ABC分類，分類的原則主要是貨架距離I/O的距離，見表2。

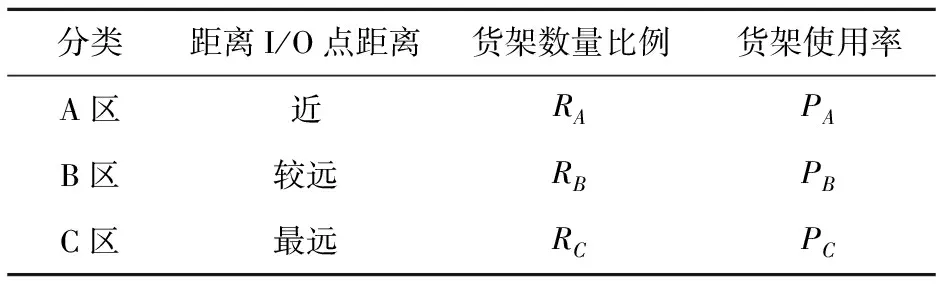
表2 倉庫貨架ABC分析表

在倉庫的實際使用過程中，貨物的存儲往往要結合適當的存儲策略，常用的存儲策略有隨機存儲、定位存儲、分類存儲等方式。在一般情況下，貨位分配的優化目標主要有兩個[10]：

(1)使貨架的重心最小，以滿足貨架穩定性的要求。

(2)對存取效率的要求，頻繁存取的物品應放在能夠快速取到的位置上。

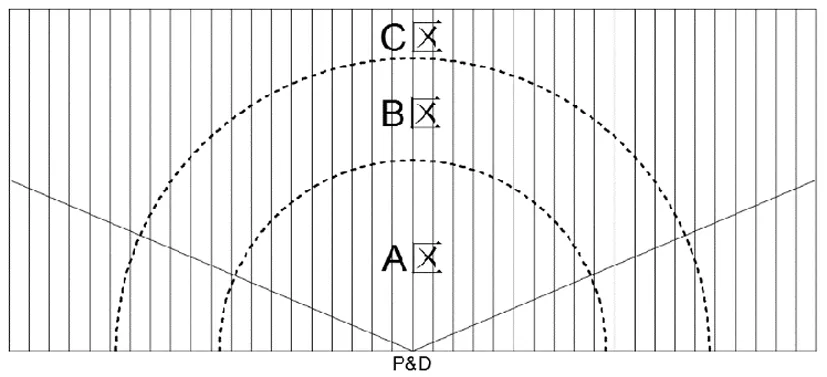
圖5 按貨物周轉率劃分倉庫區域

在此假設所研究的是單層貨架倉庫，在倉庫的設計時，考慮產品入庫貨位分配時主要考慮基于產品出入庫頻度的貨位分配原則。如圖5所示，在倉庫中，根據表1中的原則按貨物周轉率對貨物進行分類，A類貨物周轉率最高，C類貨物周轉率最低，在倉庫的實際使用中，應該將周轉率越高的貨物存放地離P&D點越近，故可以對應的對倉庫進行分區，A區、B區、C區分別放置對應周轉率的貨物，這樣有利于貨物的存取。

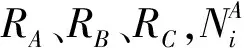
(11)

并且有：

(12)

在考慮pi的值時，可以依據倉庫所存儲不同種類貨物所占比重和周轉率進行設置。則倉庫所對應的平均揀貨距離如下:

(13)

則優化的目標函數為：

(14)

2 V型布局算法設計

2.1 算法設計

粒子群優化(Partice Swarm Optimization，PSO)算法于1995年由Kennedy和Eberhart[11]兩位博士提出，該算法通過模擬自然界中的鳥群的覓食運動來實現對于最終問題的求解。PSO算法一經出現即引起了廣大學者的研究興趣，目前已經廣泛用于解決各類優化問題，但是經典PSO算法也存在易陷入局部最優以及算法性能問題，本文采用極值擾動算子，結合并行搜索策略，提出一種改進粒子群優化算法(particle swarm optimization algorithm with extreme disturbed operator, EDO-PSO)求解，利用極值擾動算子解決算法易于陷入局部最優的問題；并采用并行搜索策略，將粒子種群按粒子適應度大小分成兩個子種群，適應度較好的子種群采用較小的慣性權值進行局部搜索，適應度較差的子種群采用較大的慣性權值進行全局搜索，以此增強種群的尋優能力，并與其他改進粒子群算法用Benchmark函數對比驗證算法有效性。

假設倉庫的布局是對稱分布的，所以只需對倉庫的一側進行建模分析。倉庫共有2n+1條揀貨通道，每一列貨架有h個貨位，則問題的維度為n維(b0=w)，可行域為(0,h)。問題對應的解為[b0,b1,b2,b3,…,bn],則倉庫的V型主通道即為b0,b1,b2,b3,…,bn所對應的點依次連接而成的通道。粒子群的規模為M，算法迭代次數為eranum，則粒子i在第t次迭代過程中所達到的位置狀態表示為：

Xi(t)={xi1(t),xi2(t),…,xin(t)},i=1,2,…,M

(15)

粒子的飛行速度定義為：

Vi(t)={vi1(t),vi2(t),…,viN(t)},i=1,2,…,M

(16)

則粒子i在第t時刻的第j(j=1,2,…,n)維的飛行速度調整為下式：

vij(t)=εvij(t-1)+c1r1[r3pij-xij(t-1)]+

c2r2[r4gj-xij(t-1)]

(17)

(18)

其中，c1和c2為加速因子，通常c1和c2均取2，r1和r2是[0,1]內的隨機數，pij為粒子i在t時刻第j維粒子自身所經過的最佳位置，gj為整個種群第j維上的最優值，tg為極值擾動閾值，sg為算法停滯代數。

在粒子群算法中，當粒子的速度超出了上下極限時，則粒子的速度則被固定為極限值。即：

(19)

ω為慣性權值，ω值較大時，可以增強全局搜索能力；反之，ω值較小時，可以增強算法的局部搜索能力。所以選取合適的ω值對算法的影響很大，有很多學者提出了動態慣性權重調整策略，Y.Shi和R.C.Eberhant首先提出了慣性權重典型線性遞減策略[12]，之后有學者提出了很多不同的非線性[13]和自適應慣性權重策略[14,15]，大大的改進了粒子群算法的性能。主要的思想是考慮到在算法初期，應該保證慣性權值ω足夠大并且減小的速度較小以此來使得粒子能夠更好的搜索全局最優解，在算法后期慣性權值可以快速減少以此在之前搜索到的解附近搜索最優解，加速收斂。

本文采用一種并行搜索的方法，即對每次迭代后的種群按照適應度值分為兩個小種群，種群1(pop1)是適應度較好的個體組成的種群，種群2(pop2)是適應度較差個體組成的種群,種群1與種群2的大小為2：1，本文中采用的種群數大小為30，則種群1有20個粒子，種群2有10個粒子。對于個體適應度較差的種群，則在下次迭代中使用較大的慣性權值；對于個體適應度較好的種群，在下次迭代中使用較小的慣性權值。

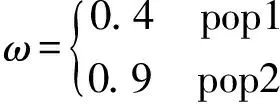
(20)

并且為了更好的尋找最優解，種群1采用深度搜索策略，即令c2=0，讓粒子從自身最優位置進行學習。此時速度的更新公式為：

vij(t)=ωvij(t-1)+c1r1[r3pij-xij(t-1)]

(21)

參考文獻[16]，通過嚴格的數學推導，可以得到:

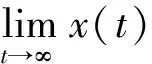
(22)

所以當算法處于進化停滯時，粒子群中的粒子都會出現早熟，如果所有粒子在靠近p*的過程中沒有找到比pg更好的解，則算法即陷入局部最優解。為了算法能夠突破進化停滯的局面，更好的尋找最優解，所以采用局部擾動策略，該策略引進了進化擾動代數，增加了極值擾動算子，當算法進化出現停滯時，則使用極值擾動因子調整pb和pg，對個體極值和全局極值同時進行隨機擾動，使粒子向新的p*靠近，從而使粒子快速跳出局部極值點。

本文中當全局極值pg連續tg代沒有改變時，本文中tg設置為20，則通過極值擾動因子同時調整當前的個體極值pb和全局極值pg，通過使粒子轉向新的搜索路徑和區域來幫助粒子跳出局部最優解。

粒子i在t時刻的位置更新可由下列公式計算所得：

xij(t)=xij(t-1)+vij(t)

(23)

2.2 算法實現

輸入：n(揀貨通道的數量);a(相鄰揀貨通道的間距);h(倉庫的寬度);pi(每條揀貨通道上進行存取貨物作業的概率);w(通道寬度的一半)。

輸出：主通道的最優位置bi

Step1輸入倉庫的參數n，a，h，pi，w。

Step2初始化粒子群算法參數eranum，popsize,c1,c2,tg。

Step3算法開始,初始化種群。

Step3.1更新gbest, pbest。

Step4判斷是否達到迭代次數，如果否則繼續，如果是則繼續Step5。

Step4.1按照公式(17)(21)(23)分別更新種群1和種群2中每個粒子的速度和位置。

Step4.1.1判斷速度是否越界，如果是則按公式(19)更新速度。

Step4.2根據公式(14)評估每個粒子的適應度函數。

Step4.3更新每個粒子的歷史最優。

Step4.4更新群體的全局最優。

Step4.5按照粒子適應度大小將種群分成兩個小種群。

Step4.6判斷迭代次數是否滿足擾動條件，如果是則按公式(18)進行擾動Step4.6.返回Step4。

Step5算法結束，輸出最優主通道的位置。

2.3 算法性能分析

為了說明本算法的有效性，本實驗選用了幾個經典的Benchmark函數來檢驗算法的性能，表3中給出了各測試函數的表達式、取值范圍和達優值，所有的測試函數均取30維，并且函數的最優值均為0。算法編程用matlab 2015b工具實現，計算機CPU為2.60GHz。

其中，函數1，函數2為單峰值函數，Sphere函數是簡單的單峰值函數，可以檢驗算法的執行性能；Rosenbrock是一個比較復雜的非凸病態函數，其全局最小值位于一個平滑的、彎曲路徑上的谷底，所以該函數在一般情況下很難搜索到最優解，故通常用該函數來評價智能優化算法的性能。函數3、函數4、函數5都是多峰函數，都有很多個局部極小值點，一般都較難搜索到全局最優解，所以通常用這些函數來檢驗函數的跳出局部最優解的能力。

表3 測試函數

所有實驗的種群規模均取30，迭代次數為1000次，每個函數的測試獨立運行100次，算法參數設置同前文。為了說明優化粒子群算法的性能，將本文算法和動態改變慣性權值的自適應粒子群算法(DCWPSO)[17]、慣性權重線性下降的標準粒子群算法(LWPSO)[12]、均勻搜索粒子群算法(UPSO)[18]進行比較，對比組的算法參數設置與參考文獻中相同，得到優化結果平均值、方差和達優率作為算法的衡量標準，測試結果如表4所示。

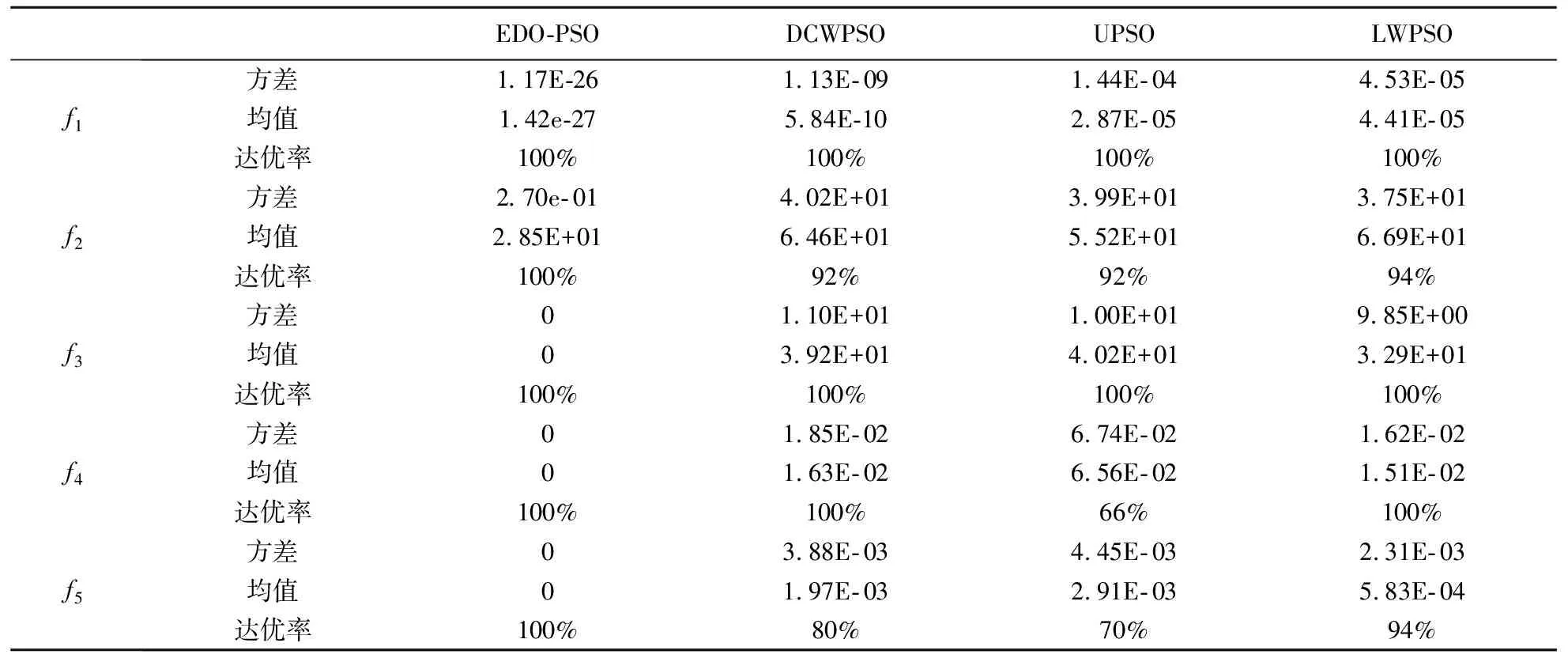
表4 測試結果

從表4中的數據可以看出，周期性極值擾動因子可以有效地幫助算法跳出局部最優解，大大的改善了算法的性能，而采用了并行搜索策略和深度搜索策略，使得粒子能夠快速的收斂到較優的解，相比于其他改進粒子群算法有明顯的優勢。為了更好的說明算法性能的改善，針對函數2、函數3、函數4、函數5這四個復雜的優化函數做出平均適應度變化曲線。為更直觀的對比各算法的性能，對適應度取對數后做適應度隨時間的變化曲線，四個Benchmark函數對應的進化曲線如圖6所示。

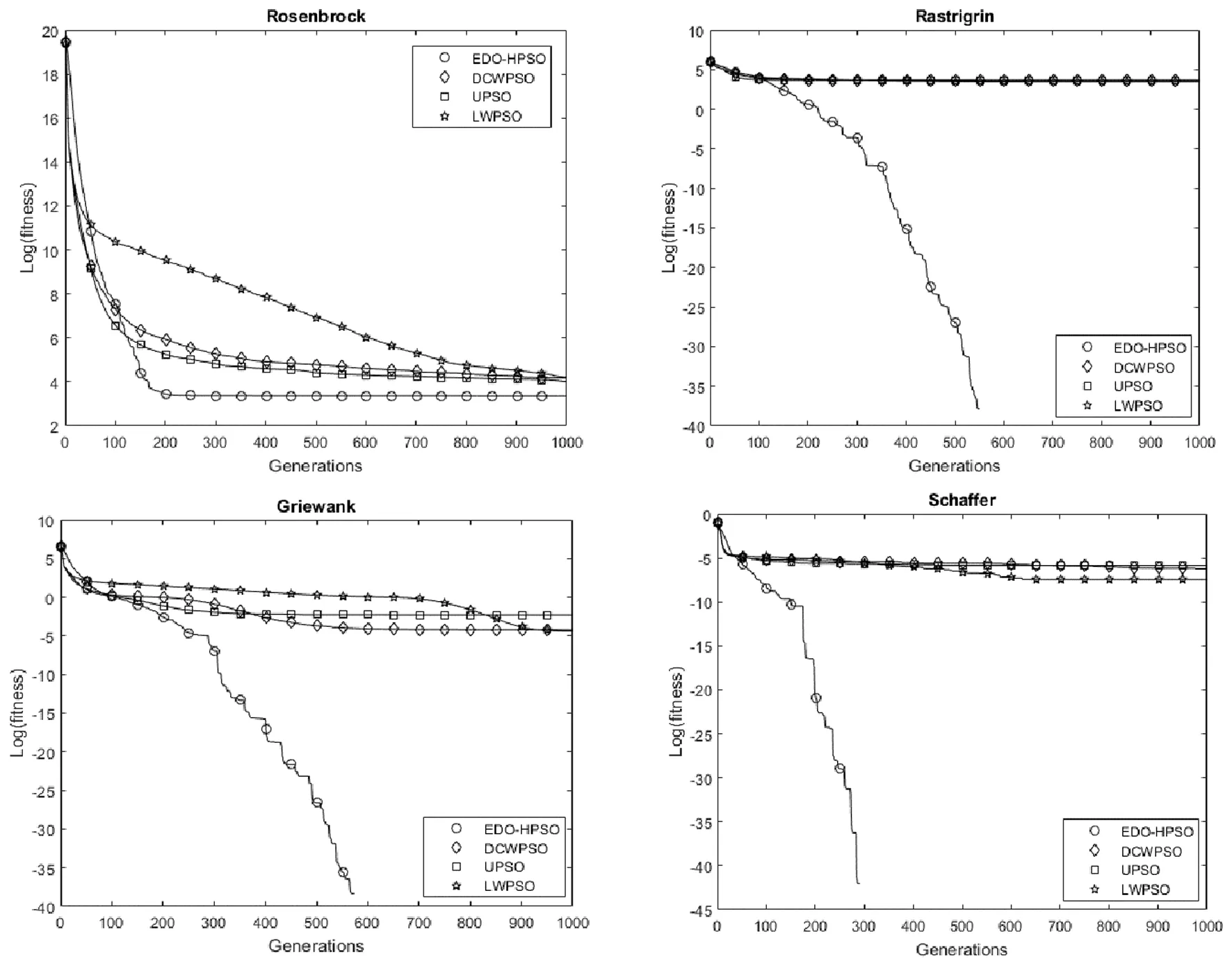
圖6 測試函數平均適應度變化曲線

從平均適應度變化曲線中可以看出，本算法在求解Rastrigrin、Griewank和Schaffer函數時能夠很好的跳出函數的局部最優解，較快的收斂到函數最優解，在求解Rosenbrock函數時有較快的收斂速度，雖然收斂的結果相對于其他算法沒有很大的優勢，但是算法的穩定性很強，算法最終結果的方差明顯優于其他算法，并且達優率能夠達到100%。從表4和圖5的測試結果中可以看出，本算法有很好的尋優能力，下文中將該算法應用到倉庫的主通道設計的求解當中。

3 案例分析

3.1 方案設計

參照文獻1，設揀貨通道和主通道的寬度均為2.5個單位，相鄰揀貨通道之間的距離為4.5個單位。根據物動量ABC分析按根據貨物周轉率由大到小計算累計周轉率比率，周轉量累計百分數在60%～80%之間的定為A類，周轉量累計百分數在20%～30%之間的定為B類，其余定義為C類。將不同的貨物進行分類并存儲到指定區域，而在相應的區域內貨物的存儲是遵循隨機原則。針對公司H的倉庫訂單進行EIQ-ABC分析的結果如表5所示，按照如圖4的方式和表5中的數據進行倉庫分區，則最靠近P&D點的3/10區域存放A類貨物，倉庫中間3/10區域存放B類貨物，遠離P&D點的4/10區域存放C類貨物。

表5 倉庫貨架ABC分析表

在倉庫規模相同的情況下，給出兩種設計方案，方案一是倉庫共有21條揀貨通道，每一列貨架有100個貨位；方案二是倉庫共有41條揀貨通道，每一列貨架有50個貨位。

針對假設的倉庫，結合倉庫分區標準，方案一中根據公式(11)計算結果大致得出人工去到不同揀貨通道進行揀貨作業的概率依次為:

p0～10=[0.0558 0.0558 0.0555 0.0547 0.0531

0.0516 0.0488 0.0462 0.0423 0.0368 0.0273]

方案二中人工去到不同揀貨通道進行揀貨作業的概率依次為：

p0～20=[0.0464 0.0464 0.0461 0.0453 0.0439 0.0421

0.0403 0.0374 0.0334 0.0276 0.0185 0.0141

0.0133 0.0125 0.0112 0.0086 0.0073 0.0073

0.0073 0.0073 0.0073]

(因為倉庫布局是對稱分布，所以只列出了從通道0開始的倉庫右側通道所對應的概率)。

3.2 仿真結果

利用本文中的提出的改進粒子群算法EDO-PSO，在matlab中實現，按照前文中建模推導出的公式(14)為目標函數。按照上文中設定的算法參數，迭代次數為3000，運行求解后的結果如下：

對于方案一，w=1.25,a=4.5,h=100,n=10橫向通道的節點bi如下：

b0～20=[1.25,8.28,14.66,20.49,25.83,

30.75,35.28,39.48,43.36,46.96,50.31]

對于方案二，w=1.25,a=4.5,h=50,n=20,橫向通道的節點bi如下:

b0～20=[1.25,5.972,10.12,13.86,17.1,19.89,22.49,

24.76,26.69,28.33,29.86,31.05,32.26,33.16,

33.8,34.51,34.96,35.44,35.94,36.44,36.6]

所得結果如圖7、圖8所示。按照相同的分配策略，兩種方案的平均揀貨距離相對傳統型的雙分區型倉庫布局的對比如表6所示。

圖7 21條揀貨通道設計結果示意圖

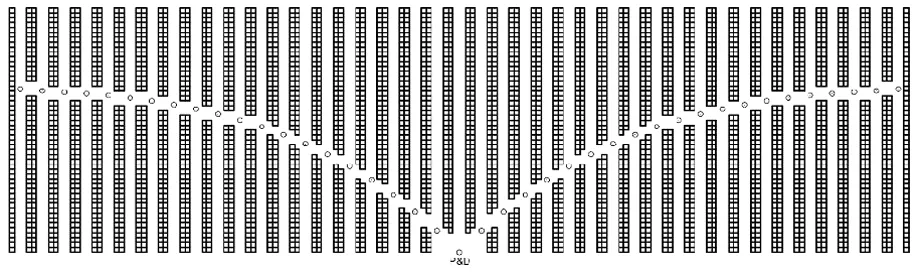
圖8 41條揀貨通道設計結果示意圖

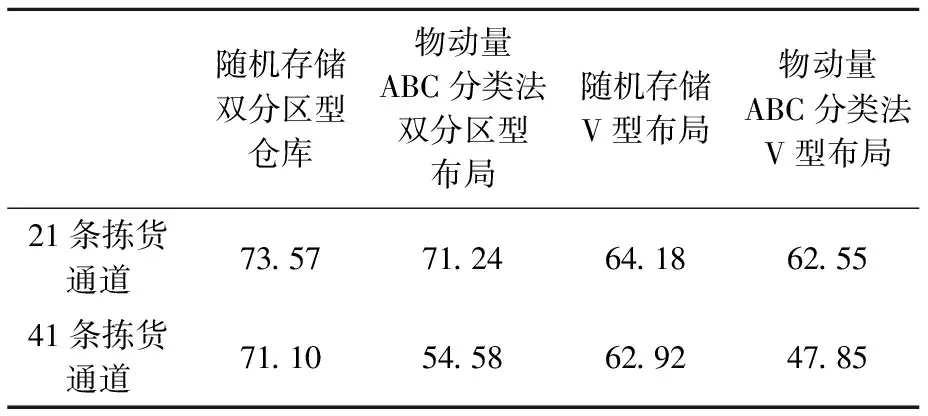
隨機存儲雙分區型倉庫物動量ABC分類法雙分區型布局隨機存儲V型布局物動量ABC分類法V型布局21條揀貨通道73.5771.2464.1862.5541條揀貨通道71.1054.5862.9247.85

從仿真的結果中可以看出，物動量ABC分類法更加適合長寬相差較大的倉庫，因為這種倉庫人工去到最里面的貨架進行倉儲作業需要更長的路程，則應盡量減少這一部分貨架的使用率，即用這一部分貨架存儲物動量較小的貨物，因此物動量ABC分類法在這一類倉庫中應用的效果會更加明顯。

4 結語

論文在Flying-V型倉庫布局的基礎之上，考慮傳統型人工揀貨方式的倉庫，每次存取單個貨物，結合物動量ABC分析法對倉庫進行分區，基于非完全隨機的分配原則來建立主通道設計模型，提高倉庫的運作效率。并對粒子群算法進行改進，用Benchmark函數對比檢驗改進粒子群算法的性能，并應用于符合實際約束問題中，能夠較快的得到滿意的結果，實驗結果表明該方法有效應用于V型倉庫主通道設計中，在物動量ABC貨位分配策略下，相比隨機策略的主通道設計方案能夠有效的減少倉庫平均揀貨距離，提高倉庫的運作效率。