以匹配課堂的數學文化作為探究的抓手

孫曉紅

【摘要】依據史海尋根——課堂匹配——活動支撐——效果檢測——拓展延伸這四大關鍵環節，讓數學史從歷史知識形態走向教育教學形態融入小學數學課堂。基于數學史實去琢磨數學家曾經走過的彎路、碰到的認知障礙，才會對數學教育有新的感悟，才能有效實現數學文化在課堂教學中的有機融入，有效發展理性思維。

【關鍵詞】數學文化 ? 課堂 ? 探究 ? 抓手 ? 理性思維

數學學科本身有著漫長的發展之路，每一個定理，每一個分支，每一段歷史，每一個國家，每一個數學家等都有著鮮明的歷史印跡。能沉淀下來的，保留至今的都是寶貴的財富。學生在課堂上遇到的學習障礙正是數學家曾經遇到過的。我們學習數學的過程，應該和人類認識數學的過程一樣。我們應該按照數學發展歷史的順序學習數學，體會數學發展的每個瓶頸，體會先有直觀思維再給出形式化描述的艱難。只有理解人類如何獲得某些事實或概念的知識，我們才能對學生應該如何獲得這樣的知識做出更好的判斷。

學情調研（問題調研+訪談）

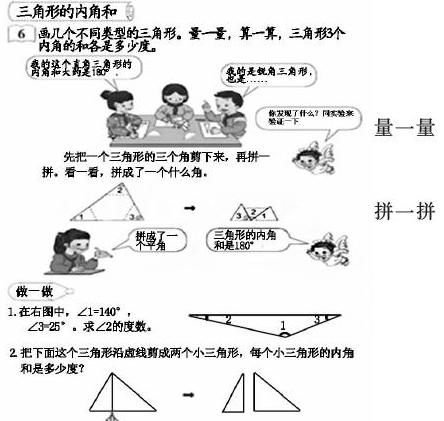
1.三角形內角和是多少度？

2.你是怎樣得出來的？（量、拼、折）

3.你當時得到的每次剛好都是180°嗎？你確信你拼的一定是一個平角嗎？

4.你現在確信三角形內角和一定是180°嗎？

從調研結果和訪談看，有一些學生對任意三角形內角和是180°存有質疑。從E、F兩個班的數據來看沒有質疑，調查了解到這個教師比較權威化，對學生要求也嚴格，他所帶的學生必須聽話，所以學生從來不質疑。探究時最后一個角很多學生是算出來的，并沒有真正去量。 ? ? 其他班也存在這樣的情況，當孩子在課前從教師、書本等不同渠道得到這一結論時，他們的做法是什么？（1.更改角的度數，湊180°;2.量2個角，第三個是算出來的）因為四年的學習經驗就已經告訴學生，教師和課本永遠是對的。

更改數據背后反映的是什么？學生不質疑、不求真的學習態度與習慣！對于前面四個班的還有質疑火花的孩子們，如果我們置之不理，他們在若干年以后是否也就成了前一批直接更改數據的孩子呢？對這些存在質疑的孩子，我們應該如何幫助他們呢？

比較有意思的是，同樣的問題，在經歷了一年的成長之后，對五年級學生做追蹤調研，數據出現了變化。

追蹤調查D班學生，這節課的內容是蘇教版四年級下冊，這學期他們上升到五年級，同樣的上面4個問題，統計結果如下：

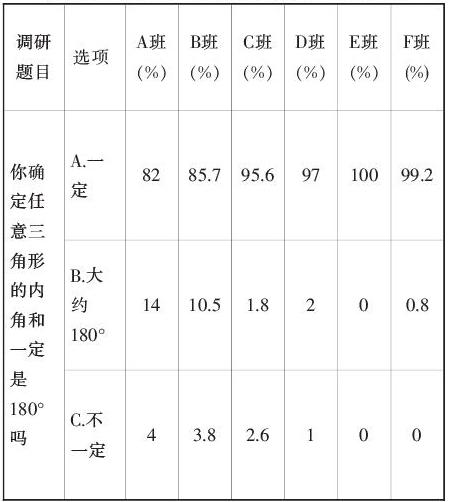
隨著年齡的增長，一句“因為有誤差，大家測量的不夠準確，正確的應該是180°”，一直是孩子心中的一個結，有的孩子認為，自己已經盡心盡力的測量，已經夠準確了，“誤差”這個詞的理解，學生心理接受是有一定困難的。

思考：

1.測量三個角，然后相加，是誰想出來的？

2.內角和是180°的結論是誰發現的？

3.教學中怎樣引導學生去發現這個結論？

4.初中幾何證明添加輔助線是怎么想到的？

5.怎樣給學生解釋小學測量有誤差？

……

不鼓勵學生問什么，不講證明，數學就失去了靈魂！是否可以在課堂上引入小學生能理解的更為嚴謹的證明呢？利用符合學生心理特點的理性思維來避開“誤差”帶來的尷尬，使得實驗幾何向論證幾何邁出一小步。

依據筆者課堂實踐總結的經驗：史海尋根—課堂匹配—活動支撐—效果檢測—拓展延伸這四大關鍵環節，讓數學史從歷史知識形態走向教育教學形態融入小學數學課堂。

史海尋根：三角形內角和的發現與證明—泰勒斯、畢達哥拉斯、帕斯卡、歐幾里得……

通過與古人的深入“交流”體驗，運用古人解決問題的方式、方法把“實踐操作”和“演繹推理”結合起來，讓孩子了解數學的本質，培養理性精神，觸摸數學的靈魂。構思出如下課堂結構：

基于以上分析，制定如下目標：

1.經歷從特殊到一般的推算三角形內角和的方法，質疑結論的正確、真實，以及方法的科學性，培養學生崇尚真理、探求真知的科學思維和精神。

2.觸摸數學歷史，感受數學文化，挑戰數學家，養成勇于挑戰，能做和數學家一樣的事，提升探究的勇氣。學習主動探究新知的方法，了解轉化遷移的數學思想，發展合情推理和演繹推理能力。

3.通過數學拓展，將數學知識與“紅色文化”有機融合，提升學科育人功能。

實踐操作

通過課前的一個話題：老師和老黃牛比，有什么不同？從學生的回答中引出“問”與“思”，本節課從問與思開始，經歷問什么，思什么，最后明白怎么問，怎么思。在這個過程中體驗科學的質疑、求真之道，這是課堂的明線。然后再把四個關鍵環節有機融入“推理+計算=推算環節”多種方法進行說理，這個活動的放手使得學生在探究中呈現出了異彩紛呈的創新。現擷取幾個精彩片段：

一、引導質疑、聚焦問思

師：運用這些方法，得出的三個內角的和都是180°嗎？為什么？

依據學生的問題：三個內角的和到底是不是180°？量的時候有多有少啊？拼的也不見得平，所以不是很準確！為什么要讓我們往一起拼，和是怎么想到的？……相機板書：180°？、不準確、怎么想到和？（其實這是對知識的三種質疑——結果的正確性、方法的科學性、知識的來源）

二、匹配課堂、推算說理

（一）推算活動

師：用這些方法得出的三角形內角和是180°并不能使我們信服，看來我們需要尋求另外的途徑，也就是思考怎樣解決（板書：怎樣解決）。其實，關于內角和是多少度我們可以從前面的一些經驗中得出，比如正方形的內角和是多少度？

生：360°。

師：你怎樣得出的？

生：每個角都是90°，4×90°=360°。

師：聽出來沒有，就剛才這位同學所說的，其實就是推理+計算（板書：推算）。通過推算，得出正方形的內角和是360°，你確信嗎？（確信）這就是數學中的講道理，通過推算，以理服人。

師：你覺得哪類三角形的內角和與正方形最有關聯？（等腰直角三角形）你能像剛才這樣推算出等腰直角三角形的內角和嗎？

學生想出從對角線分割360°÷2=180°

師：推理加計算，你們認可這個結論嗎？

我們這時候能不能下結論說，所有任意直角三角形的內角和是180°？

生：不能，目前只能得到等腰直角三角形的內角和是180°。

師：如果要得到所有直角三角形內角和是180°，還得研究誰？它又會與哪個圖形聯系緊密呢？

生：還得研究一般的直角三角形，它與長方形聯系緊密。我們也可以把長方形分割成兩個直角三角形，然后用360°÷2=180°得出一般的直角三角形內角和是180°。

師：這時，我們可以下結論說（學生說出，任意直角三角形內角和是180°）。

要想得出任意三角形內角和是180°，你覺得還得研究哪些三角形？

出示研學單：

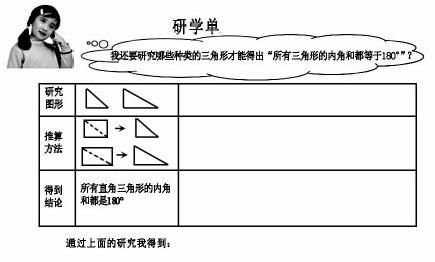
這個研學單與一般的學習單不同的地方在于，一般的學習單是老師設計好的學習過程，學生只需按要求操作就可，思維含量低。這個研學單是放手讓學生自己設計下一步研究的方向，主動探究、思考，更利于學生的素養落地。而由正方形開始到最后探究得出任意三角形內角和是180°的由特殊到一般的思維過程，正是當年12歲的帕斯卡得出的方法。據說他是用炭塊在墻上完成的。這個環節我不是像貼標簽式的講述一段歷史，而是通過設計匹配的活動，讓學生重走數學家的道路，體會能做和數學家一樣的事。當學生經歷由一般到特殊的過程，最后得出結果，筆者說出，剛才我們探究的過程就是神童數學家帕斯卡12歲發現的方法，你們才11歲，比他還厲害以后肯定會成為數學高手的時候，學生的那種自豪感，對數學探究的激情洋溢于表。

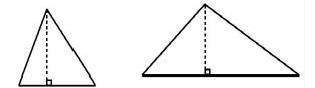
孩子們大多通過做高，轉化為兩個直角三角形，180°×2=360°，360°-90°×2=180°推算出銳角三角形、鈍角三角形，最后得出任意三角形內角和事180°。由于放手讓學生研究，匯報中的那些有問題的學生通過其他學生的質疑、互辯，精彩不斷。

2、體驗活動

師：開始的時候有同學問道，和是怎么想到的？據說與希臘的大數學家泰勒斯有關，他有一次用等邊三角形磚鋪地的時候發現了等邊三角形內角和是180°。你們能利用下面的圖說說為什么嗎？

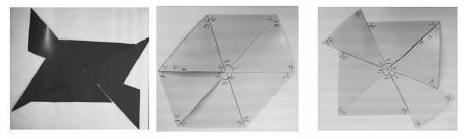
善于思考的泰勒斯想，其他的三角形會是怎樣呢？

請同學們以四人小組為單位，分別用六個同樣的等腰三角形或六個同樣的不等邊三角形來拼圖，感受泰勒斯當年的探究“三角形內角和為180°”的發現過程。

學生通過拼圖、說明，重溫了泰勒斯當年的過程。以下為學生部分作品。

數學文化的有機融入，一定要有匹配的活動，讓學生去體驗，而不是一句口號，而且這樣以文化為暗線的活動是學生探究的有效抓手。

三、拓展延伸、效果檢測

（一）拓展

師：同學們，我們剛才的拼圖還有這樣的驚喜呢！你們看：

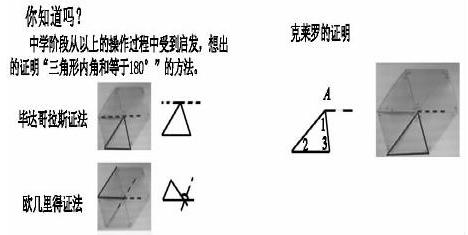
為學生呈現初中論證的源頭，體會知識的鏈接，為后續的學習鋪好道路。

（二）檢測

1.變與不變

仔細觀察在千斤頂下放的過程中，三角形的內角是怎樣變化的？其中什么沒變？

（2）算一算

紅領巾的這個角師多少度

五角星的這個角是多少度？

本節課學生經歷了數學發現的理性道路：特殊到一般歸納思維方式，學會了以理服人。學生學習數學的過程是數學史的快進，怎樣能自然的融入，達到潤物細無聲的有機匹配，筆者上面的實踐提供了一種可參考的途徑即：史海尋根—課堂匹配—活動支撐—效果檢測—拓展延伸 。以匹配的數學文化為探究的抓手，實踐證明學生喜歡上這樣的課，學生在這樣的課中素養提升效果明顯。