基于STEM理念的小學(xué)數(shù)學(xué)“綜合與實踐”整合設(shè)計

江瀾

《義務(wù)教育數(shù)學(xué)課程標(biāo)準(zhǔn)（2011年版）》指出：“綜合與實踐”內(nèi)容設(shè)置的目的在于培養(yǎng)學(xué)生綜合運用有關(guān)的知識與方法解決實際問題，培養(yǎng)學(xué)生的問題意識、應(yīng)用意識和創(chuàng)新意識，積累學(xué)生的活動經(jīng)驗，提高學(xué)生解決實際問題的能力。小學(xué)數(shù)學(xué)“綜合與實踐”的綜合性不僅表現(xiàn)為數(shù)學(xué)內(nèi)部各領(lǐng)域間的綜合、數(shù)學(xué)與其他學(xué)科的綜合、數(shù)學(xué)與學(xué)生日常生活的綜合，也體現(xiàn)在解決問題的過程中要求學(xué)生的各種能力、各種方法、各種工具的綜合。其使命在于給學(xué)生一個綜合應(yīng)用所學(xué)數(shù)學(xué)知識、方法，去實際解決一個數(shù)學(xué)內(nèi)部或生活問題的機會，它的教育價值取向正與STEM理念相一致。

【教學(xué)目標(biāo)】

1. 通過測量竹竿影子長度的實踐活動，主動探索、掌握影子長度與目標(biāo)物實際高度之間的比例關(guān)系。

2. 通過合作探究的方式，利用發(fā)現(xiàn)的規(guī)律解決“大樹有多高”問題，設(shè)計測量金字塔高度的方案。

3. 在解決問題過程中，感受數(shù)學(xué)與科學(xué)、工程、技術(shù)的密切聯(lián)系，進一步激發(fā)學(xué)習(xí)數(shù)學(xué)的興趣，培養(yǎng)創(chuàng)新精神和問題解決能力。

【教學(xué)重難點】

溝通數(shù)學(xué)與科學(xué)的知識聯(lián)系，綜合運用多學(xué)科知識和方法，系統(tǒng)地經(jīng)歷解決問題的過程——設(shè)計、表達、實踐、檢驗、反思、調(diào)整。

【教具準(zhǔn)備】

課前：米尺，卷尺，計算器，紙筆，竹竿若干組（每組竹竿1米、50厘米各一根，另外兩根長度不限），小木棒若干。

課堂上：小木棒若干、手電筒、尺子、紙筆、計算器。

【課前預(yù)習(xí)】

一、測影長

1. 六人一組，將班級分成若干組。

2. 每組2把卷尺和1組竹竿。另備好計算器、紙和筆。

3. 測前思考：為了能使測量的數(shù)據(jù)盡量精確，測量時應(yīng)該注意些什么？

如：竹竿不能傾斜，要與地面垂直;手扶竹竿，不能放在竹竿的頂端，否則會影響影長的數(shù)據(jù);身體不能擋住竹竿的影子;等等。

4. 各小組自選一個地點，把幾根長度不同的竹竿直立在地面上，量出此時每根竹竿的影長，記錄在表里，并計算比值。（測量時都取整厘米數(shù)，竹竿長與影長的比值保留兩位小數(shù)）

完成測量記錄單（要求填寫各組竹竿長、影長、竹竿長與影長的比值等數(shù)據(jù)）。

二、搭支架

參考金字塔圖片，用小木棒等搭建金字塔的支架模型。

設(shè)計意圖：將“綜合與實踐”的教學(xué)活動僅當(dāng)成一節(jié)課，這樣的理解是狹隘的，實施是單一的。嘗試以“長作業(yè)”的形式實施“綜合與實踐”活動，能夠使課堂上的探究時間更加充裕。課前先讓學(xué)生進行不同長度竹竿的影長測量、比值計算，以及用小木棒等搭建金字塔的支架模型，有助于課堂上集中時間和精力探究數(shù)學(xué)問題。

【教學(xué)過程】

一、知識喚醒，打通聯(lián)系

觀看三組圖片：（1）兩個身高不同的學(xué)生走在路上，投下了長短不同的兩個影子。（2）陽光下物體的影子在一天中的變化。（3）某天早上九點時，1米長的竹竿在不同地點的影子。

師：我們在科學(xué)課上學(xué)習(xí)了影子的知識，說一說這三組圖片中蘊含的影子知識。

引導(dǎo)學(xué)生總結(jié)：（1）學(xué)生通過觀察個子高，影子就長;個子矮，影子就短，初步感知影長和身高之間存在一定的規(guī)律（正比例）。（2）物體的影子在一天中有方向和長短的變化，當(dāng)光線與水平線的夾角為直角時，影子的長最短，當(dāng)光線與水平線的夾角越來越小時 ，影子的長度越來越長 。（3）同一時刻，不同地點的影子長度不同。

設(shè)計意圖：在五年級科學(xué)課上，學(xué)生已學(xué)習(xí)了太陽和影子的科學(xué)知識，本環(huán)節(jié)喚醒學(xué)生大腦中與影子相關(guān)的科學(xué)知識，為溝通本課主題、解決問題做好準(zhǔn)備。

二、交流數(shù)據(jù)，發(fā)現(xiàn)規(guī)律

各小組交流匯報課前測量的數(shù)據(jù)。

師：為什么同樣長的竹竿大家量出的影長卻不同？

說明：因為各組測量的時間、地點可能不同，所以同樣高度的直立竹竿的影長也在發(fā)生變化。

師：比較求得的比值，你有什么發(fā)現(xiàn)？

小組討論、合作交流，從而發(fā)現(xiàn)規(guī)律：在同一地點，同時測量不同的竹竿，高度與影長的比值是相等的。

三、深入探究，理解本質(zhì)

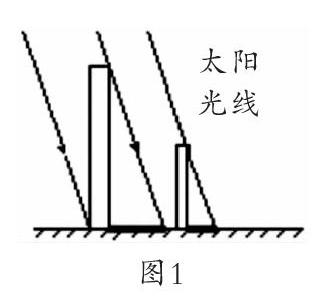
1. 課件呈現(xiàn)測量情境示意圖（圖1）。

師：把不同長度竹竿端點和各自的影子端點連起來，有什么發(fā)現(xiàn)？

生：形成了幾個直角三角形，它們形狀一樣，但大小不一樣。

課件動態(tài)演示把兩個直角三角形相應(yīng)的角重疊。

師引導(dǎo)：這兩個直角三角形對應(yīng)角分別相等，其實，這樣的三角形關(guān)系，叫作相似三角形，到了中學(xué)會深入研究它們。相似三角形一個重要的特征就是對應(yīng)的邊長比值相等，所以我們大多數(shù)小組計算出的不同竹竿的長度與影長的比值是相等的。

反思：為什么有的組計算出的結(jié)果卻不是完全一樣的呢？可能是什么原因？

（如：竹竿不垂直，測量數(shù)據(jù)有誤差，沒有在同一時刻，等等。）

2. 師：根據(jù)上面的發(fā)現(xiàn)，猜想一根3米長的竹竿，當(dāng)時直立在地面上的影長是多少？

設(shè)計意圖：學(xué)生通過觀察每組求得的比值，分析討論，發(fā)現(xiàn)規(guī)律：在同一地點，同時測量不同的竹竿，高度與影長的比值是相等的。發(fā)現(xiàn)規(guī)律后，教學(xué)并未止步。筆者通過形象圖示和直觀演示，將該部分知識與中學(xué)的相似三角形知識聯(lián)系，使學(xué)生了解規(guī)律背后的數(shù)學(xué)知識本質(zhì)。學(xué)生在反思計算結(jié)果不一致的過程中，積累了實際操作的經(jīng)驗，因此對規(guī)律的理解更深入，為后續(xù)運用規(guī)律解決問題提供理論支撐和操作經(jīng)驗支撐。讓學(xué)生進行規(guī)律的逆向運用，發(fā)展學(xué)生的思維能力。

四、設(shè)計實施，解決問題

1. 挑戰(zhàn)1：大樹有多高？

（1）出示問題：根據(jù)上面的發(fā)現(xiàn)，能算出學(xué)校里這棵大樹的高度嗎？

小組交流合作：應(yīng)該準(zhǔn)備哪些工具？需要測量哪些數(shù)據(jù)？測量時有哪些注意點？

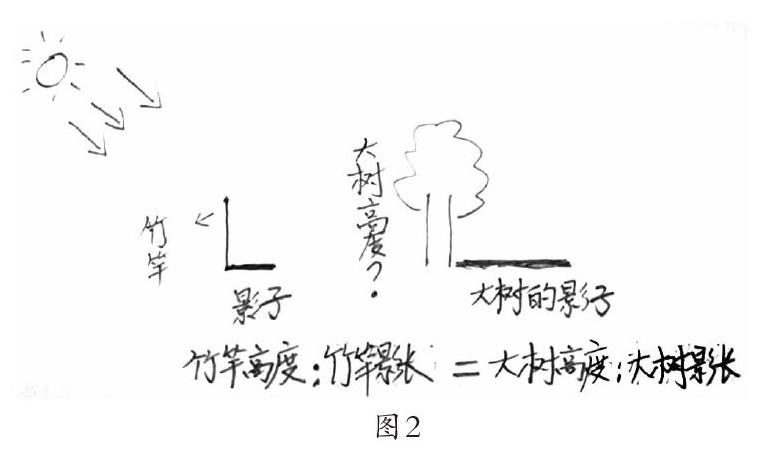
畫出測算情境示意圖。（圖2）

學(xué)生在小組交流后明確：在計算時，可以先算出竹竿長與影長的比值，再運用比值求出大樹的高度。

師：在測量竹竿的影長之后，如果過了一段比較長的時間，再去測量大樹的影長。那么，這樣計算出的結(jié)果還準(zhǔn)確嗎？為什么？

（2）出示具體情境進行計算。

如果某一時刻，身高1.6米的小麗在陽光下的影長為2.5米，一棵大樹的影長為5米，那么大樹的高度是多少？

設(shè)計意圖：讓學(xué)生利用發(fā)現(xiàn)的規(guī)律測量大樹的高度，在問題解決的過程中采用小組合作探究的方式，以三個探究問題作為腳手架——“應(yīng)該準(zhǔn)備哪些工具”“需要測量哪些數(shù)據(jù)”“測量時有哪些注意點”，并要求學(xué)生畫出示意圖，將測量的方法外顯為直觀方式，整個合作探究過程重視培養(yǎng)學(xué)生思考的有序性、邏輯性、嚴(yán)謹(jǐn)性，以及思維表達能力。

2. 挑戰(zhàn)2：金字塔有多高？

課件展示：金字塔是世界八大奇跡之一。看著這一巍峨的建筑，很多人都不禁猜測它到底有多高。但當(dāng)時沒有先進的測量儀器直接測出金字塔的高度，你能根據(jù)今天所學(xué)，設(shè)計出測量金字塔高度的方案嗎？

（1）在設(shè)計前，我們先來看看哪條是金字塔的高？

明確：金字塔的高是指從金字塔頂點向底面作的垂線。

（2）小組合作探究。

①設(shè)計測量方案（重點寫出所需工具及用途，需要測量的教據(jù)，測算步驟，注意點），畫出測算過程示意圖。

②以課前制作的金字塔支架模型為測量對象，選用合適的工具（如手電筒），進行現(xiàn)場模擬測量（根據(jù)問題情境，不能直接測出金字塔的高度，金字塔框架各邊長可以直接測量）

（3）修改調(diào)整。

根據(jù)設(shè)計方案測算出金字塔模型的高度后，直接測量模型的高度，通過對比實際高度與測算結(jié)果，檢驗測算方案是否科學(xué)合理，進行方案的修改調(diào)整。

設(shè)計意圖：在STEM教育中，整合和設(shè)計必不可少。從教育科學(xué)原理的角度來說，STEM教育要培養(yǎng)的是學(xué)生的遷移能力，引導(dǎo)學(xué)生能夠把一個情境中學(xué)到的知識運用到另一個情境中。在“大樹有多高”的問題解決之后，讓學(xué)生進入“金字塔有多高”這個問題情境，通過合作探究的方式運用知識和方法遷移，進行方案設(shè)計和現(xiàn)場模擬測算，在解決過程中，學(xué)生需要綜合運用多學(xué)科知識和方法。如設(shè)計和測算中需要運用數(shù)學(xué)的比例知識、流程圖設(shè)計以及直觀圖示的方法，在實施操作中需要控制光源與水平線的夾角來調(diào)整影子的方向和長度。活動中注重學(xué)生系統(tǒng)地經(jīng)歷解決問題的過程——設(shè)計、表達、實踐、檢驗、反思、調(diào)整，發(fā)展學(xué)生的多學(xué)科知識整合運用能力以及邏輯思維能力，強調(diào)成長型思維模式的培養(yǎng)。

五、微課延伸，拓展思考

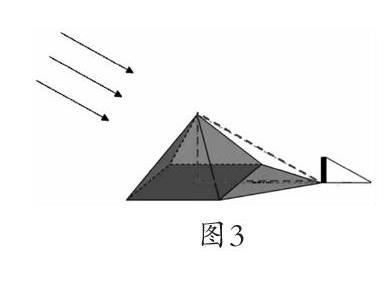
1. 觀看內(nèi)容為泰勒斯借助太陽光線測量金字塔高度的微課。（圖3）

2. 對比反思。

你們的設(shè)計方案和泰勒斯的方法一樣嗎？存在什么共同點和不同點？

核心問題①：為什么計算時要用金字塔底面邊長的一半加上外面的影長？

核心問題②：為什么泰勒斯要等到他的影長與身高相等時再去測量金字塔的影長呢？

生反饋：金字塔底面邊長的一半加上外面的影長才能和金字塔的高構(gòu)成一個直角三角形，才能利用相似三角形的邊的比例關(guān)系計算出金字塔的高度;當(dāng)泰勒斯身高與影長相等時，身高與影長的比值是1，這時金字塔高度與金字塔影長的比值也是1。所以，金字塔的高度等于金字塔影子的長度加上底面邊長的一半，省去了計算環(huán)節(jié)。

設(shè)計意圖：觀看內(nèi)容為泰勒斯利用太陽的光線測量金字塔高度的微課，讓學(xué)生親歷經(jīng)典數(shù)學(xué)問題的解決，而后引導(dǎo)學(xué)生對比和反思自己設(shè)計的方案和泰勒斯的方法有哪些相同點和不同點，見賢思齊，得到進一步優(yōu)化思維方式的機會。

（作者單位：福建省廈門市松柏小學(xué) 責(zé)任編輯：王彬）