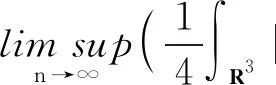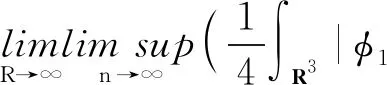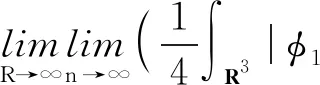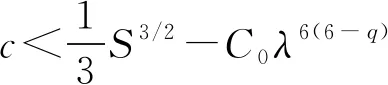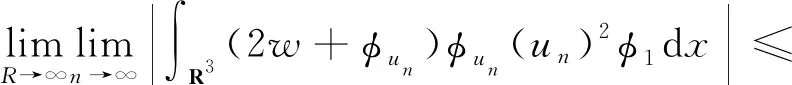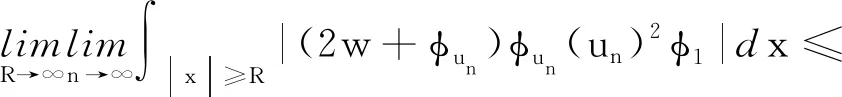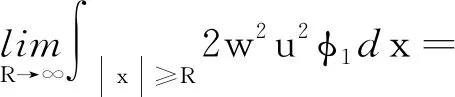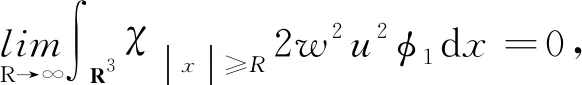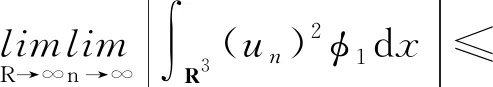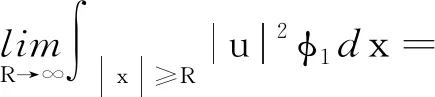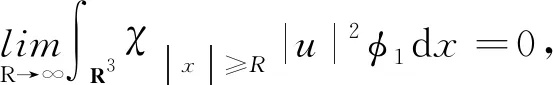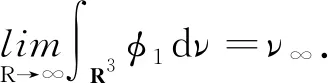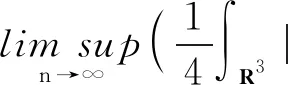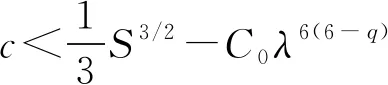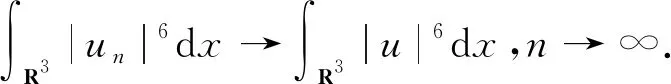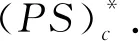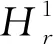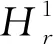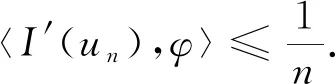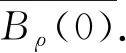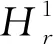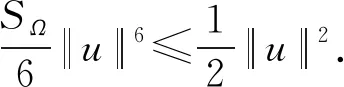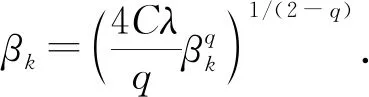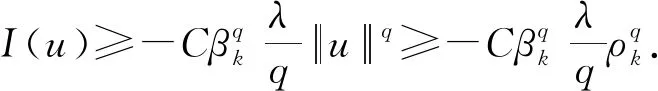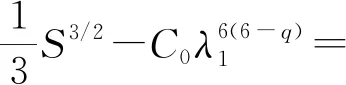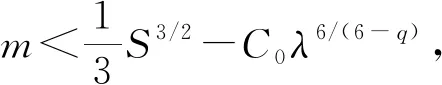帶有臨界項(xiàng)的Klein-Gordon-Maxwell系統(tǒng)解的存在性

杜玲玉, 李安然

(山西大學(xué) 數(shù)學(xué)科學(xué)學(xué)院, 山西 太原 030006)

受文獻(xiàn)[1-2]中的研究方法啟發(fā),本文主要討論式(1)負(fù)能量解的存在性結(jié)果, 其中q∈(1,2),w≥0以及λ>0.

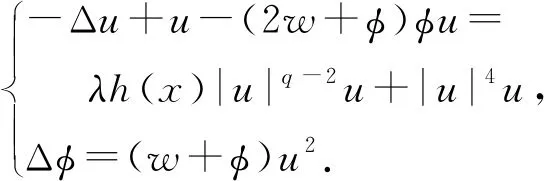
(1)

(2)

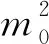
x∈R3,

(3)

在文獻(xiàn)[5]中,Cassani研究了帶有臨界項(xiàng)和低階擾動(dòng)的Klein-Gordon-Maxwell系統(tǒng)(即式(3)),并得到如下結(jié)論:

(1) 當(dāng)|m0|>|w|,40,式(3)存在一個(gè)徑向?qū)ΨQ解;

(2) 當(dāng)|m0|>|w|,q=4,且當(dāng)μ非常大時(shí),式(3)存在一個(gè)徑向?qū)ΨQ解.

1 主要結(jié)果

本文主要研究帶有臨界項(xiàng)的Klein-Gordon-Maxwell系統(tǒng)的一列負(fù)能量解的存在性.首先,我們假設(shè)函數(shù)h滿足以下條件:

(h1)h∈L2/(2 - q)(R3),h≥0,并且h?0;

(h2)h∈L6/(6 - q)(R3),h≥0,并且h?0.

定理1 假設(shè)條件(h1)或(h2)成立,則存在λ*>0,當(dāng)λ∈(0,λ*)時(shí),系統(tǒng)(K)存在一個(gè)解(u,φu)∈E×D1,2(R3).

定理2 假設(shè)條件(h1)且(h2)成立,則存在λ1>0,當(dāng)λ∈(0,λ1)時(shí),系統(tǒng)(K)存在一列趨于0的負(fù)能量解.

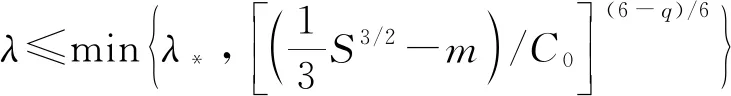
定理4 假設(shè)條件(h1)且(h2)成立,則當(dāng)λ∈(0,λ1)時(shí),系統(tǒng)(K)存在基態(tài)解.

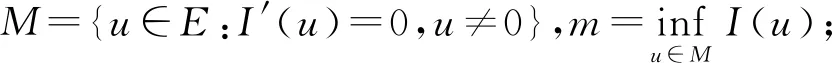
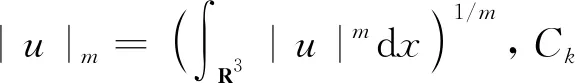
2 主要結(jié)果的證明

引理1E緊嵌入Lp(R3),p∈(2,2*).

命題1 對(duì)每一個(gè)u∈E,存在唯一的φu∈D1,2(R3),使得(u,φu)成為系統(tǒng)(K3)的解,并且有下面的結(jié)論成立:在集合{x∈R3:u(x)≠0}上,有-w≤φu≤0成立,其中w>0.更進(jìn)一步,可以得到:

證明 根據(jù)Lax-Milgram定理,可以得到系統(tǒng)解的存在性和唯一性.在第二個(gè)方程的兩端同時(shí)乘以(w+φu)-=min{w+φu,0},得到:

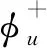
當(dāng)w>0時(shí),就有φu≤0.

現(xiàn)在,定義系統(tǒng)(K)相應(yīng)的能量泛函I:E→R為

根據(jù)h1,h2的假設(shè)條件和命題1,知道I的定義是合理的,且I∈C1(E×D1,2,R),

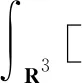
容易知,泛函I的臨界點(diǎn)是系統(tǒng)(K)的弱解.

引理2 存在λ*>0,α>0以及ρ>0使得當(dāng)λ∈(0,λ*),‖u‖=ρ時(shí),I(u)≥α.

證明 下證當(dāng)條件(h2)成立時(shí),結(jié)論成立.

根據(jù)命題1,H?lder不等式,Soblev不等式以及|u|D1,2≤|u|,可以得到:

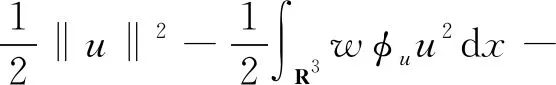
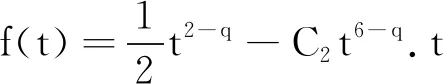
命題2 (對(duì)偶噴泉定理I∈C1(R3,R)且I(u)=I(-u),當(dāng)k∈N,存在ρk>rk>0使得:

(B1)ak∶=infu∈Zk,‖u‖=ρkI(u)≥0,當(dāng)k→∞;

(B2)bk∶=maxu∈Yk,‖u‖=rkI(u)<0;

(B3)dk∶=infu∈Zk,‖u‖≤ρkI(u)→0,當(dāng)k→∞;

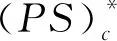
那么I有一列臨界點(diǎn)序列{uk},I(uk)→0.

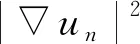
存在可數(shù)集J,{xj}?R3,j∈J,使得

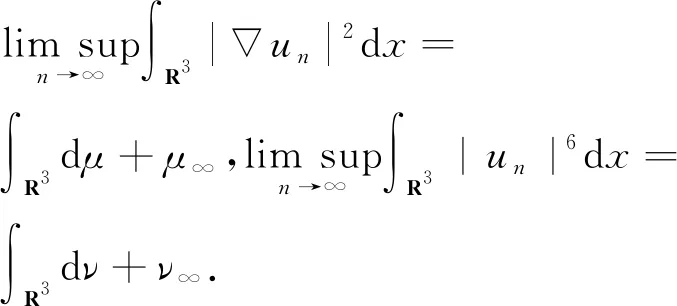
進(jìn)一步,有下面的式子成立:

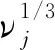
其中S是最佳Soblev嵌入常數(shù),δxj是xj處的Direc測(cè)度.

易知存在{νn:n∈N|?E,{φn:n∈N}?E*使得:

(1) 〈φn,νm〉=δn,m,其中當(dāng)n=m時(shí),δn,m=1,當(dāng)n≠m時(shí),δn,m=0;

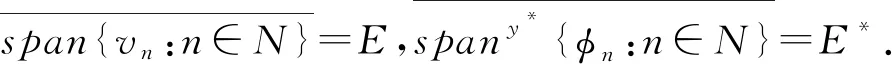
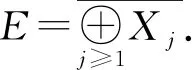
引理4 如果滿足條件(h1),(h2)時(shí),則I就滿足(PS)c序列,

證明 設(shè){un}是E中的(PS)c序列,即{un}→∞,I(un)→c,使得

根據(jù)E連續(xù)嵌入到Ls(R3),s∈[2,6],所以有

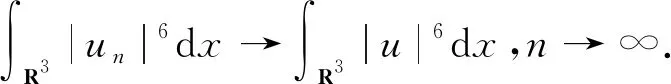
(4)

令截?cái)嗪瘮?shù)φ≡1,當(dāng)x∈B(xj,ε);φ≡0,當(dāng)x∈B(xj,2ε)c,|

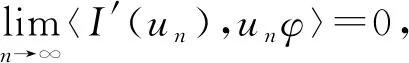
另一方面,

由式(5)～式(10)可得μi≤νi.代入得νi≥S3/2或νi=0.另外,根據(jù)Holder和Young不等式,有

定義截?cái)嗪瘮?shù)φ1≡1,當(dāng)|x|≥2R;φ1≡0,當(dāng)|x|

同時(shí),有式(12)成立:

同前面證明類似,

另一方面,

(15)

(16)

(17)

由式(12)～式(17)可得μ∞≤ν∞.代入可得ν∞≥S3/2或ν∞=0.

若ν∞≥S3/2成立,則可得:

又因?yàn)?/p>

即

即

(21)

由〈I′(un),un〉=o(1)可以得到

又因?yàn)椤碔′(u),u〉=o(1),可以得到

由式(20)～式(23)可得到:

令t→0,得出

(24)

把式(24)中的φ換成-φ,就得到

(25)

由式(26)和式(27),結(jié)合式(20)和式(21)可以得到:

定理2的證明 定義

(2) 因?yàn)閅k是有限維空間.它上的所有范數(shù)都等價(jià),對(duì)任意rk>0足夠小,命題2(B2)都成立.

因?yàn)棣耴→0,ρk→0.于是就有,當(dāng)k→∞時(shí),命題2(B3)都成立.

根據(jù)命題2,定理2成立.

定理4的證明 由定理1可知M非空,從而m的定義是有意義的.根據(jù)m的定義,存在{un}∈M是一個(gè)(PS)m序列,通過(guò)引理4和定理2就有I(u)=m,從而定理4得證.