有交互影響的三因素方差分析的應用及MATLAB實現

郭 萍

(青島理工大學琴島學院 基礎部, 山東 青島 266106)

方差分析是科學試驗及數據統計分析中的重要方法之一,它主要用于對試驗結果數據變動的分析,了解哪些因素對指標產生顯著影響[1].文獻[1-5]中給出了單因素、雙因素及三因素方差分析的原理,本文簡化了文獻[5]中有交互影響的三因素方差分析的計算方法, 同時利用簡化方法編程計算了具體的數學建模案例,并通過MATLAB實現了該案例的求解.

1 有交互影響的三因素方差分析原理[5]

設有3個因素A、B、C,因素A取r個水平,分別記為A1,A2,…,Ar,因素B取s個水平,分別記為B1,B2,…,Bs,因素C取t個水平,分別記為C1,C2,…,Ct,在水平組合(Ai,Bj,Ck)下樣本相互獨立[4]且Xijk～N(μijk,σ2),i=1,2,…,r,j=1,2,…,s,k=1,2,…,t.

數學模型為:

故檢驗假設為:

有交互影響的三因素方差分析表見表1.

表1 有交互影響的三因素方差分析表[5]Table 1 Three-factor variance analysis with interaction

檢驗規則為:

(1) 若FA>Fα(r-1,rst(m-1)),則拒絕H01,認為因素A對指標值的影響顯著;

(2)若FB>Fα(s-1,rst(m-1)),則拒絕H02,認為因素B對指標值的影響顯著;

(3)若FC>Fα(t-1,rst(m-1)),則拒絕H03,認為因素C對指標值的影響顯著;

(4)若FAB>Fα((r-1)(s-1),rst(m-1)),則拒絕H04,認為因素A與B交互作用顯著;

(5)若FAC>Fα((r-1)(t-1),rst(m-1)),則拒絕H05,認為因素A與C交互作用顯著;

(6)若FBC>Fα((s-1)(t-1),rst(m-1)),則拒絕H06,認為因素B與C交互作用顯著;

(7)若FABC>Fα((r-1)(s-1)(t-1),rst(m-1)),則拒絕H07,認為因素A、因素B與因素C交互作用顯著.

2 簡化算法

為了簡化數據輸入的工作量,同時也為了計算的簡便,可以將初始數據進行“歸整變換”,變換后再參與運算,即將初始數據減去一個常數,該常數為平均數附近的數值,然后乘上10的冪次,將小數點移去,即Y=10k(X-a).此變換后,數據是一些具有較少位數的整數,而且F值不變,這使得計算過程得到了很大的簡化.

3 數學建模案例求解及MATLAB實現

3.1 數學建模案例

某集團為了研究商品銷售點所在的地理位置、銷售點處的廣告和銷售點的裝潢這3個因素對商品的影響程度,選了3個位置(如市中心黃金地段、非中心的地段、城鄉結合部),兩種廣告形式,兩種裝潢檔次在某個城市進行了搭配試驗.表2是銷售量的數據,在顯著水平0.05下,檢驗不同地理位置、不同廣告、不同裝潢下的銷售量是否有顯著差異[6].

表2 銷售量數據Table 2 Sales data

3.2 數學建模案例的MATLAB實現

MATLAB[7]統計工具箱中用ANOVAN作多因素方差分析.有交互影響的三因素方差分析命令為[p,t]=anovan(x,group,model,sstype,gnames),返回值p,當p>α時接受H0,說明因素對指標值無顯著影響,當p<α時拒絕H0,說明因素對指標值有顯著影響,t為方差分析表.

編寫程序如下:

clc,clear

x1=[957 939 920 860 850 832 865 850 880 820 863 812];

group={[′A1′;′A1′;′A1′;′A1′;′A2′;′A2′;′A2′;′A2′;′A3′;′A3′;′A3′;′A3′;];

[′B1′;′B1′;′B2′;′B2′;′B1′;′B1′;′B2′;′B2′;′B1′;′B1′;′B2′;′B2′;];

[′C1′;′C2′;′C1′;′C2′;′C1′;′C2′;′C1′;′C2′;′C1′;′C2′;′C1′;′C2′;]};

[p1,t1]=anovan(x1,group,2,3,{′A′;′B′;′C′})

求得p1=0.026 9,0.154 8,0.044 2,0.121 1,0.336 4,0.597 7,方差分析表,如表3.

表3 MATLAB實現的方差分析表

由于ANOVAN只能解決在3個因素影響下一組數據中兩兩因素的交互作用,無法實現3個因素的交互作用,故由表3知,第一組數據下地理位置,裝潢影響下得到的兩個p值均小于0.05,故拒絕原假設,說明地理位置,裝潢對該商品的銷售量有顯著影響.而廣告及3個因素兩兩的交互作用對銷售量沒有顯著的影響.綜上所述,為了制定該商品更好的銷售計劃,地理位置、裝潢都需要進行合理的選擇.

3.3 簡化算法求解3個因素的交互作用

由于MATLAB中已有的函數只能解決在3個因素影響下一組數據中兩兩因素的交互作用,無法實現3個因素的交互作用,故采用簡化算法求解兩組數據下3個因素的交互作用.

按照銷售數據1、銷售數據2及簡化的算法X-870,原始數據依次變為:

87,69,50,-10,-20,-38,-5,-20,10,-50,-7-58,90,53,50,0,-36,-30,0,-38,24,-30,-17,-60.

按照有交互影響的三因素方差分析原理及偏差平方和分解式, 編寫程序如下:

clc,clear

x1=[87 69 50 -10 -20 -38 -5 -20 10 -50 -7 -58 90 53 50 0 -36 -30 0 -38 24 -30 -17 -60];

t2=[sum(x1)]^2/24;

st=(87^2+69^2+50^2+(-10)^2+(-20)^2+(-38)^2+(-5)^2+(-20)^2+10^2+(-50)^2+(-7)^2+(-58)^2+ 90^2+53^2+50^2+0^2+(-36)^2+(-30)^2+ 0^2+(-38)^2+ 24^2+(-30)^2+(-17)^2+(-60)^2)-t2

a1=[87 69 50 -10 90 53 50 0];sum(a1);

a2=[-20 -38 -5 -20 -36 -30 0 -38]; sum(a2);

a3=[ 10 -50 -7 -58 24 -30 -17 -60]; sum(a3);

sa=(sum(a1)^2+ sum(a2)^2+ sum(a3)^2)/8- t2

b1=[87 69 -20 -38 10 -50 90 53 -36 -30 24 -30];sum(b1);

b2=[50 -10 -5 -20 -7 -58 50 0 0 -38 -17 -60]; sum(b2);

sb=(sum(b1)^2+ sum(b2)^2)/12-t2

c1=[87 50 -20 -5 10 -7 90 50 -36 0 24 -17];sum(c1);

c2=[69 -10 -38 -20 -50 -58 53 0 -30 -38 -30 -60]; sum(c2);

sc=(sum(c1)^2+ sum(c2)^2)/12-t2

ab1=[87 69 90 53]; sum(ab1);

ab2=[50 -10 50 0]; sum(ab2);

ab3=[-20 -38 -36 -30]; sum(ab3);

ab4=[-5 -20 0 -38]; sum(ab4);

ab5=[10 -50 24 -30]; sum(ab5);

ab6=[-7 -58 -17 -60]; sum(ab6);

sab=(sum(ab1)^2+ sum(ab2)^2+ sum(ab3)^2+ sum(ab4)^2+ sum(ab5)^2+ sum(ab6)^2)/4-t2-sa-sb

ac1=[87 50 90 50]; sum(ac1);

ac2=[69 -10 53 0]; sum(ac2);

ac3=[-20 -5 -36 0]; sum(ac3);

ac4=[-38 -20 -30 -38]; sum(ac4);

ac5=[10 -7 24 -17]; sum(ac5);

ac6=[-50 -58 -30 -60]; sum(ac6);

sac=(sum(ac1)^2+ sum(ac2)^2+ sum(ac3)^2+ sum(ac4)^2+ sum(ac5)^2+ sum(ac6)^2)/4-t2-sa-sc

bc1=[87 -20 10 90 -36 24]; sum(bc1);

bc2=[69 -38 -50 53 -30 -30]; sum(bc2);

bc3=[50 -5 -7 50 0 -17]; sum(bc3);

bc4=[-10 -20 -58 0 -38 -60]; sum(bc4);

sbc=(sum(bc1)^2+ sum(bc2)^2+ sum(bc3)^2+ sum(bc4)^2)/6-t2-sb-sc

abc=(87+90)^2+(69+53)^2+(50+50)^2+(-10)^2+[(-20)+(-36)]^2+[(-38)+(-30)]^2+(-5)^2+[(-20)+(-38)]^2+(10+24)^2+[(-50)+(-30)]^2+[(-7)+(-17)]^2+[(-58)+(-60)]^2;

sabc=abc/2-sab-sac-sbc-sa-sb-sc-t2

se=st-sa-sb-sc-sab-sac-sbc-sabc

msa=sa/2;msb=sb/1;msc=sc/1;msab=sab/2;msac=sac/2;msbc=sbc/1;msabc=sabc/2;mse=se/12;

fa=msa/mse

fb=msb/mse

fc=msc/mse

fab=msab/mse

fac=msac/mse

fbc=msbc/mse

fabc=msabc/mse

計算求得方差分析表,見表4.

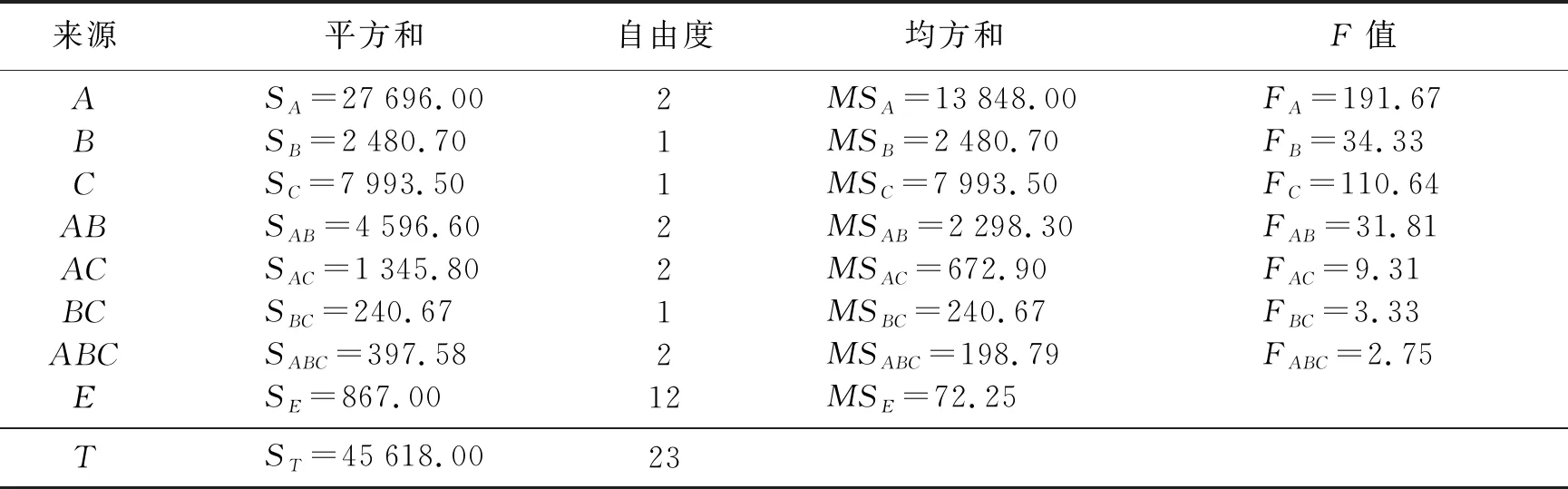
表4 方差分析表Table 4 The variance analysis results

由于FA=191.67>F0.05(2,12)=3.89,FB=34.33>F0.05(1,12)=4.75,FC=110.64>F0.05(1,12)=4.75,FAB=31.81>F0.05(2,12)=3.89,FAC=9.31>F0.05(2,12)=3.89,所以在α=0.05顯著性水平下,因素A、因素B和因素C的不同水平都對該商品的銷售量有非常顯著的影響, 因素A,B和因素A,C兩兩的交互作用對該商品的銷售量有顯著影響.又由于FB C=3.33

4 結 語

本文基于有交互影響的三因素方差分析原理,針對地理位置、銷售點處的廣告和銷售點的裝潢這3個因素對商品的影響程度,采用MATLAB進行求解,但MATLAB中的函數具有一定的局限性.故對算法進行了簡化,并利用簡化算法對該案例進行求解.結果表明該算法具有實用性和可行性.