精準診評答疑解惑，經典習題同類跟進
—— 從幾則“在線”答疑案例說起

☉江蘇省蘇州市工業園區東沙湖學校西校區 左愛娟

鄭毓信教授曾在《人民教育》發表系列文章推介數學教師的專業基本功，如“善于舉例”“善于提問”“善于比較和優化”，這些在課堂教學中顯得非常重要.除此之外，個別輔導或作業批改時，教師還需要具備答疑解惑的專業功夫.最近“在線”給學生的一些錯題進行診評并答疑輔導，取得較為理想的答疑效果，引發筆者對“在線”答疑輔導的一些思考.檢索文獻，發現早有“先行者”（詳見參考文獻［1］～［2］）.本文先梳理幾個“在線”答疑的案例，并闡釋相關思考，供研討.

一、“在線”答疑輔導案例展示

題1：如圖1，在四邊形ABCD中，AC=BD=6，E、F、G、H分別是AB、BC、CD、DA的中點，則EG2+FH2=______.

思路診評與點撥：從學生標注的4個3及EG⊥HF看，思路已接通，可能是運算上出錯.一個有效的建議是，設GE、FH交于O點，恰當設元，設HO=x，GO=y，由勾股定理得x2+y2=9，待求的GE、FH的平方和是4（x2+y2）=36.可見，幾何演算類問題，恰當引入參數可以簡化推理演算的表達式，使得我們避免復雜大寫字母的運算處境，這是值得分享和積累的經驗.

圖1

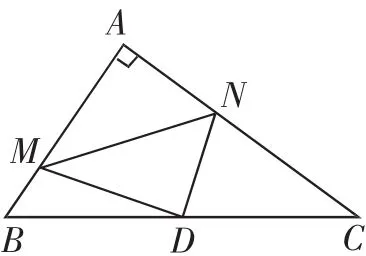
圖2

題2：如圖2，在Rt△ABC中，∠A=90°，AB=6，AC=8，點D為邊BC的中點，點M為邊AB上的一動點，點N為邊AC上一動點，且∠MDN=90°，則cos∠DMN為______.

思路診評與點撥：學生原有思路（過點M、N作兩條垂線段）雖然有一些進展，但對于目標（∠DMN的余弦值）沒有很快接近，反而陷入復雜的運算.這種輔助線構造不利于接近目標，需要“折返”“調頭”.（隨感：一個優秀學生、有智慧的人應該有“調頭”的勇氣）

思路1：過點D分別向AB、AC作垂線段DG、DH，垂足分別為G、H，可利用相似三角形處理……最終導出DN∶DM的值，這是∠DMN的正切值，思路就接通了.

思路2：把目光投向四邊形AMDN，雙垂直？對角互補嗎？是否四點共圓？確認這些之后，連接AD，可將∠DMN轉化為∠DAN，從而快速轉化為∠C的正切值，答案只需口算.（當然，運算簡單的方法需要付出邏輯思維的代價.對于一名優秀學生來說，應該思路開闊，即“思維向四面八方打開”）

題3：將一副三角板（如圖3）擺放在一起，組成四邊形ABCD，連接AC，則tan∠ACD的值等于______.

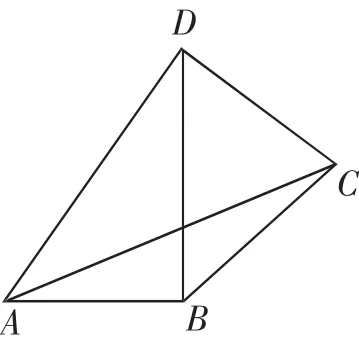
圖3

思路診評與點撥：學生原有作高（作AC邊上的高）的想法，沒有走通，但這種念頭是有效的，可以調整為構造CD邊上的高AF，將“右下角”補全成等腰直角三角形BDE，就能順利突破思路.這里有一個關鍵是“增量巧設”（與學生原有設法相比，更有利于后續演算），即設AB=a，于是可得出BD=BE=a，BC=CE=a，再把目光投向等腰直角三角形AEF，就可想清CF、AF的長了，從而獲得思路貫通.

題4：二次函數y=ax2+bx+c（a≠0，a、b、c為常數）的圖像如圖4所示，則ax2+bx+c=m有實數根的條件是______.

思路診評與點撥：學生原有答案（-m≥5）莫名其妙，解集表達形式上怎么也不能寫-m啊.直接看出答案，視ax2+bx+c=m左邊為圖中拋物線“不動”，將右邊視為動直線y=m，可直觀看出直線與拋物線有交點時，m≥-2.這道題的解題策略是“以形助數”，提供以下兩道習題，作為同類跟進.

圖4

圖5

同類鏈接1：二次函數y=ax2+bx+c的圖像如圖5所示，試分析關于x的方程ax2+bx+c-3=0的根的情況.

同類鏈接2：若二次函數y=x2+bx的圖像的對稱軸是經過點（2，0）且平行于y軸的直線，則關于x的方程x2+bx=5的解為（ ）.

A.x1=0，x2=4 B.x1=1，x2=5

C.x1=1，x2=-5 D.x1=-1，x2=5

二、關于答疑解惑的幾點思考

1.深刻理解習題結構，能從不同角度貫通思路

給學生答疑輔導之前，需要先深刻理解習題的結構特點，嘗試從不同的角度貫通思路，并且明辨不同解法的繁簡、優劣，這樣才能站在更高的高度理解學生的思路、錯誤及思維障礙之處.特別是，教師的解法研究要盡可能體現“回到定義”的“初等解法”，因為當學生思路受阻時，需要及時引導他們回到“回到定義”的“自然而然的解題念頭”，而不是簡單化地轉化為一些個性化的“模型”“模式”.當然，一些重要的“解題模型”、轉化策略或求解經驗也可通過由簡單的問題出發幫助學生推導確認，用于一些較難習題的有效轉化.這些理解習題的功夫其實都是后續精準診評、解惑的基礎.

2.認真閱讀學生解法，讀懂已有進展精準診評

教師在深刻理解習題的結構與解法之后，接下來就是認真分析學生的解法，由于在線答疑并不是面批或當面答疑，所以無法開展即時對話，特別是學生對問題有怎樣的理解進展、想法只能根據“圖片”（更多情況下是所拍照片）上遺留下來的一些解題痕跡，如演算草稿或圖形上的分析痕跡進行診評.根據這些答題痕跡，我們要嘗試理解學生的思考方向、已有進展，并開展精準診評、提出解題建議，在引導解題思路時最好能從學生已有進展或已有念頭出發，使之不斷豐滿，接近解題目標，如果出現錯誤的解題方向，則需要恰當引導，讓學生有“敢于調頭”的解題勇氣和智慧.

3.經典習題解法錯漏，需要同類跟進修補漏洞

答疑解惑過程中遇到的習題會有很多類型，教師在遇到一些經典習題時，要保持敏感，引導學生重視經典問題，在剖析錯誤原因、貫通思路之后，要引導學生進行解后回顧與反思：還有哪些解法？不同解法需要體現哪些領域的知識或性質定理？等等.在此基礎上，需要像上文“題4”一樣，給出同類習題的鏈接跟進，讓學生在訂正之后有同類題的變式再練，以有效提高對這類習題的處理能力.

4.答疑解惑是基本功，值得教師長期修煉精進

師者，所以傳道授業解惑也.數學老師的答疑解惑能力應該是一項專業基本功，這項專業基本功的背后是教師扎實的解題能力，閱讀、傾聽學生的能力，恰當、精準診評學生的能力，特別是，除了解題思路的貫通，還要向學生傳遞解題信心，鼓勵學生不怕困難、迎難而上，又要有善于調頭、回到起點再出發的勇氣.此外，答疑輔導不宜直接告知答案或思路，要通過恰當的設問與誘導，使學生能自主發現解題思路并獲得最后解答，這樣對于保護學生的解題信心是非常重要的.

三、寫在后面

教學即研究，教育現場無處不在.本文關注的是答疑解惑這個常見的教學話題，但是“至小無內”，如果深入下去，不同教師的答疑解惑的水平和功夫差異是巨大的，當我們以精湛的答疑解惑能力呈現在學生面前時，收獲的是教師的專業威信，還有來自學生和家長的敬佩.讓我們共同努力，期待更多答疑解惑案例的分享，促進這類課題的研究更豐富和深入.