研讀課本教出深度，示范引領促進理解
—— 以七年級“不等式性質”教學為例

☉江蘇省海安市海陵中學 劉 生

不等式性質新授課教學是很多教研活動的熱點課題，不少老師往往類比等式性質進行不等式性質的研究，通過一些具體數運算的舉例引導學生發現不等號方向的規律，進而歸納得出不等式的性質，再進行大量的例、習題的訓練，這種教學實施當然很有實效，但是與高品質的數學教學、追求數學育人的高標準還有一定的距離.筆者所在備課組經過充分研討、集體備課生成的不等式性質課例重視由“數學現實”引入新課，并預設講授如何從一般意義驗證不等式性質，讓學生感受到一種新的數學性質的生成需要經過證明才能確認，雖然減少了訓練題的數量，但數學味兒更濃，教學效果也很好.下面先梳理該課的教學設計，并跟進教學立意的闡釋，供研討.

一、不等式的性質教學設計

教學環節（一） 創設情境，引出新知

情境引入：學習不等式之后，對于一些簡單的不等式，如x+2＞4，可以直接看出它的解集為x＞2；但對于較為復雜的一元一次不等式，如，如何求其解集呢？這就需要學習不等式的性質，然后以此為依據將復雜的不等式進行變形求解.所以本課的任務就是研究不等式的性質.

教學環節（二） 歸納規律，驗證性質

“實驗1”：已知1＜2，計算并比較：

1+3____2+3，1+6____2+6，1+2019____2+2019；

1-3____2-3，1-6____2-6，1-2019____2-2019.

規律發現：不等式兩邊同時加上或減去同一個數，不等號的方向不變.

“實驗2”：已知1＜2，計算并比較：

1×3____2×3，1×6____2×6，1×2019____2×2019；

1 ×（-3）____2 ×（-3），1 ×（-6）____2 ×（-6），1 ×（-2019）____2×（-2019）.

規律發現：不等式兩邊同時乘上同一個正數，不等號的方向不變；不等式兩邊同時乘上同一個負數，不等號的方向改變.

教學組織：在學生發現規律之后，師生合作歸納出不等式的性質的文字表達，教師將其板書在黑板的主板區，先寫出這些是“發現規律”，為了對這些規律進行驗證，教師預設以下一些方法的講授（可結合PPT進行）.

比如，利用數軸進行驗證.在數軸上由左到右取兩點A、B，對應著數a、b，a＜b.同時加上一個數，就是將A、B兩點向相同方向平移一定的距離，仍然有a+m＜b+m，an＜b-n.

對于m＞0，利用數軸演示am＜bm時，可利用乘法的本質是加法，轉化為加法進行演示說明.

對于n＜0，利用數軸演示an＞bn比較麻煩，可以利用相反數的意義，先在數軸上理解-a＞-b，再擴大幾倍理解an＞bn.

還可從一般意義進行證明，借助于作差法.

不等式性質1的證法：因為a＜b，所以a-b＜0，所以a+m-b-m＜0，即a+m-（b+m）＜0，所以a+m＜b+m.

不等式性質2的證法：因為a＜b，所以a-b＜0.又m＞0，所以m（a-b）＜0（依據：異號兩數相乘，符號為負），所以ma-mb＜0.所以ma＜mb.

不等式性質3的證法：因為a＜b，所以a-b＜0.又n＜0，所以n（a-b）＞0（依據：同號兩數相乘，符號為正），所以na-nb＞0.所以na＞nb.

說明：以上驗證或證明可結合班情、學情進行鏈接選學，待學生理解并確認之后給出不等式性質的文字、符號表達方法，形成板書.

教學環節（三） 初步運用，步步有據

例1 設a＞b，用“＞”或“＜”填空，并說明理由.

（1）a+3___b+3；（2）a-2019___b-2019；（3）-5a___-5b；

預設變式：設a＜b，用“＞”或“＜”填空，并說明理由.

（1）a+1___b+1；（2）2a-2019___2b-2019；（3）3-5a___3-5b；（4）-

教學組織：安排學生先獨立思考，再在小組內交流，并大組匯報.展示交流時，教師先示范口答的格式.如“例1（3），根據不等式性質3，不等式兩邊同時乘負5，不等式的方向改變，所以答案是-5a＜-5b”.再如變式（4）的口答格式，“先由不等式性質2，不等式兩邊同時除以5，再由不等式性質1，不等式兩邊同時減去，不等式方向都不改變”.教師示范之后，對于每道小題，至少安排2～3個學生復述.一方面，可以讓學生進一步熟悉不等式的性質；另一方面，可以促進學生區別等式性質與不等式性質的不同表達方式，這里并不是簡單的機械重復的教學行為.

教學環節（四） 課堂小結，參與究錯

小結問題1：本課所學習的不等式性質與等式性質有怎樣的關系？你是如何理解的？在小組內舉例交流.

小結問題2：運用不等式性質解以下幾個簡單的不等式：

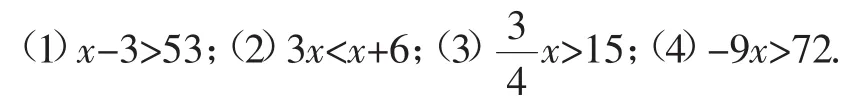
教學組織：解答展示時，需要講出具體的方法或步驟.

小結問題3：小安提出一個命題，若x＜2，則ax＜2a.

請判斷小安的命題是真命題還是假命題，并說明理由.

教學組織：先讓學生獨立思考，然后由學生評價這種解法，并進行優化改進，指出需要分類討論，這可以促進學生對不等式性質的深刻理解.

二、教學立意的進一步闡釋

（一）深入研讀教材，充分想清教材導入語的用意

本課例在開課階段的過渡語雖然簡短，但是忠實于教材，是因為想清了教材導入的意圖，也就是為什么要研究不等式的性質這個知識點：是因為解不等式時需要考慮的算理、依據就是不等式的性質，所以需要研究.如果我們忽略教材導入語的價值，認為它可有可無，則可能忽略它，從而采用其他新知導入方式.可見，不同的導入方法，背后往往體現了教者研究教材的深度與角度.

（二）針對班級學情，追求深度教學，發展核心素養

在上面的課例中，考慮到班級學情整體較好，我們不想在不等式性質的應用上加大題量進行機械訓練，降低學生學習興趣，讓一些優秀學生處于空轉狀態.所以預設了帶領學生一起理解不等式性質的證明.這是對教材上簡單的一些數據演算、發現規律、歸納性質的必要補充，讓優秀學生理解數學，懂得學習數學需要從實驗發現走向一般證明.現在大家都在倡導數學育人，發展學生核心素養，我們認為，用有數學味兒的內容來促進學生理解數學，學會研究數學，用數學的套路來研究數學，正是發展學生核心素養的重要方式.

（三）重視示范引領，通過學生不斷復述鞏固新知

不管如何重視“以學為中心”“學生為主體”，但是“關注教”“研究教”是永不過時的，也是十分必要的，教與學的研究不可偏廢.在本課例中，關于不等式性質的一般證明，需要教師的啟發式講授來節約課堂教學時間，而在應用不等式性質時，教師的示范引領作用非常關鍵，我們通過先示范講解解題方法，在學生傾聽理解之后，安排多名學生連續復述解題步驟，這個過程十分必要、非常有效.一方面，可以讓學生對不等式性質的文字表達更加熟悉；另一方面，促進學生理解不等式變形過程中的步步有據.事實上，有了這樣的過程，在不等式性質發現和歸納之后，就不需要安排學生讀記、背誦的環節（相比后面講解變形步驟，數學上使用讀背的方式容易讓學生厭煩），因為數學是需要理解和運用的.