一種微重力下洗衣裝置的設計與研究

湯凱利，張 華，鄧德喜，章松發(fā)

(無錫小天鵝股份有限公司， 無錫214028)

1 引言

長期多人載人飛行任務中，航天員的衣物如果繼續(xù)采用一次性服裝，會因為補給和運輸而造成較大的資源消耗。 為了更環(huán)保并且能夠經濟高效地解決該問題，需要設計一種微重力環(huán)境下可用的洗衣裝置，實現(xiàn)衣物的洗凈與循環(huán)使用。

微重力環(huán)境下，地面上現(xiàn)行的洗滌方法主要有以下問題：①手洗無法實現(xiàn)密封和自動化；②波輪自動洗衣機，借助離心力產生的水與衣物的作用力將衣物洗凈，無法實現(xiàn)密封；③滾筒自動洗衣機，借助離心力將動能轉化為勢能，然后自由落體，利用摔打將衣物洗凈，借助了重力。 因此需要設計一種密封良好，不利用重力的洗衣裝置，在微重力下將衣物洗凈。

本文提出一種具有柔性洗滌袋，同時柔性袋被凸包夾持擠壓且被齒輪結構驅動的洗衣裝置。由于創(chuàng)造微重力環(huán)境進行測試代價高昂且周期較長，為了衡量該洗衣裝置的洗滌力度，提升其洗凈能力，引入仿真模型指導設計和優(yōu)化。 應用光滑粒子動力學法(SPH)與有限單元法(FEM)耦合方法模擬洗衣裝置的洗滌過程。 結合所提出的洗凈經驗公式，用該模型指導洗衣裝置的結構和動力優(yōu)化設計。

2 基本設計

為實現(xiàn)密封良好，且有效提供機械力的洗滌方式，微重力下洗衣裝置的關鍵結構設計如圖1所示。 圖中略去了管道等組件，僅示意了實現(xiàn)洗滌功能的3 個主要結構，分為柔性袋組件、導軌組件和凸包組件。 其中柔性袋組件由PP 材料框架與硅橡膠片組成，可密封容納衣物與水；導軌組件位于柔性袋上下兩側，用齒輪齒條結構實現(xiàn)驅動，可帶動柔性袋組件左右往復運動；凸包組件分為前端凸包和后端凸包，固定于機器外殼上，可在柔性袋左右往復運動時，提供擠壓力。 因整機體積限制，柔性袋組件的最大運動行程為100 mm，見圖2。 所設計洗滌過程為：先放入衣物與洗滌劑，接著將柔性袋抽真空，然后進水，最后啟動導軌，開始洗滌。 洗滌過程中，袋內衣物將在機械力與洗滌劑共同作用下，將衣物洗凈。 其中機械力來源包括：柔性袋左右往復運動產生的衣物與水流的摩擦力、衣物與柔性袋PP 材料框架的撞擊力以及衣物被凸包擠壓的擠壓力。

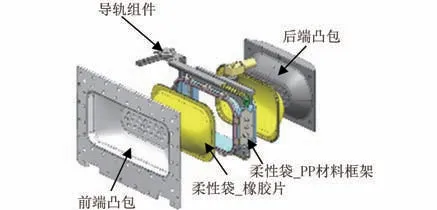
圖1 關鍵結構爆炸圖Fig.1 The exploded view of the main structures

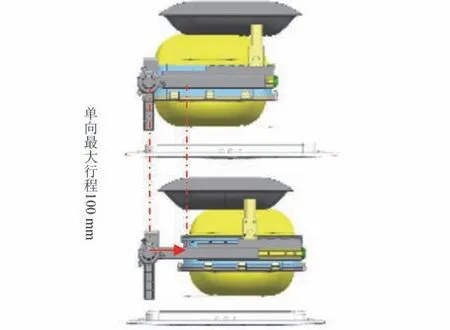
圖2 裝置最大行程示意圖Fig.2 The maximum stroke of the device

洗衣裝置初版樣機測試結果顯示衣物洗凈比明顯低于國標，根據洗凈經驗公式，洗凈參數(shù)由機械力、衣物摔打翻滾頻率以及效率共同決定，如式(1)所示：

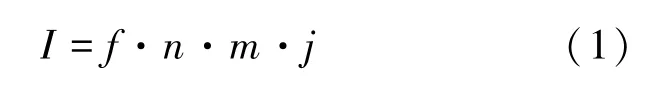
其中I 為洗凈參數(shù)，f 為洗滌過程機械力，n為衣物摔打頻率，m 為衣物翻滾頻率，j 為衣物翻滾效率。 本文針對洗滌過程機械力進行研究，并以滾筒洗凈參數(shù)為目標，對當前裝置結構和運動參數(shù)進行優(yōu)化，以提升裝置洗凈能力。

3 數(shù)值仿真

3.1 理論基礎

衡量洗滌力度的仿真模型，需考慮袋內內容物與柔性袋不斷撞擊擠壓這一洗滌過程，是1 個局部存在大變形的模擬問題。 SPH-FEM 耦合方法，能夠同時發(fā)揮SPH[1]計算大變形和FEM[2]計算精度高計算效率高的優(yōu)勢，十分適用于該類模型內局部出現(xiàn)大變形的問題。 SPH-FEM 耦合方法由Attaway 等[3-4]首先提出，Sonia 等[5]在此基礎上發(fā)展了1 種SPH-FEM 連續(xù)混合方法，根據再生階數(shù)要求，提供多種插值函數(shù)及其導數(shù)，能夠確保SPH 和FEM 的可再生性、收斂性和穩(wěn)定性。SPH-FEM 耦合在液體晃動、金屬切削、沖擊爆炸等方面都有應用[6-7]。

3.1.1 模擬流體的SPH 方程

流體控制方程由為不可壓黏性Navie-Stokes方程(簡稱N-S 方程)，即連續(xù)方程和動量方程。受重力作用的連續(xù)體(流體和固體)的運動方程均可以用連續(xù)方程和動量方程表示為式(2)、式(3)：

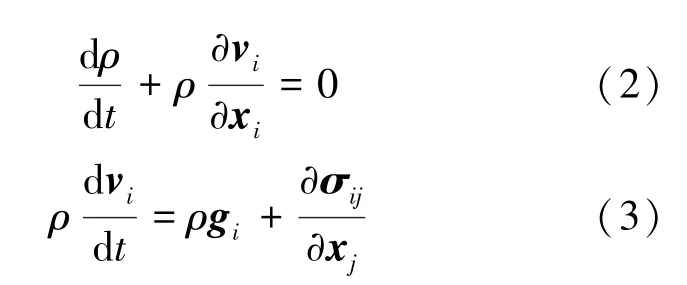
其中t 是時間，ρ 是密度， vi是速度向量， xi是位置向量，gi是重力向量，σij是應力張量。

采用光滑粒子流體力學方程時，根據定義恰當?shù)暮撕瘮?shù)的密度分布，將連續(xù)體劃分為若干質量為m 的準實體粒子，這時除在以粒子本身為圓心的沿半徑2h(h 為用來刻畫核函數(shù)尺度域的“光滑長度”)分布的圓周上的密度不為零外，其余各處均為零，據此可進行數(shù)值計算的離散[8]。

根據連續(xù)方程(2)，一般粒子α(流體或固體)的密度物質導數(shù)可以通過光滑粒子流體力學進行內插獲得式(4)：

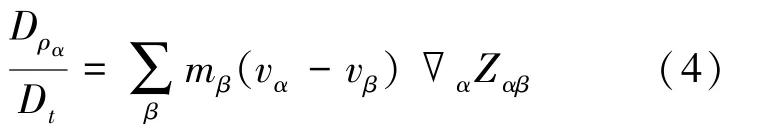
式中，對粒子α 尺度域內的周圍所有粒子β求和，使用速度差分(vα- vβ)散度的近似是為保證常數(shù)速度場的密度物質導數(shù)為零；▽αZαβ是核函數(shù)在處的梯度。 其3 次樣條曲線為式(5)：

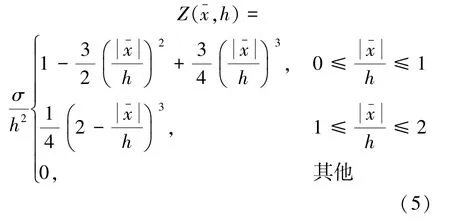
其中σ 是正交標準化常數(shù)，對于一般流體粒子α，動量方程(3)的光滑粒子流體力學方程可以寫作式(6)：

人都聚集到了北壩兩座山包間谷口處。遲恒驚慌失措趕到，不知道自己能做什么。狂潑的雨如同充滿仇恨的怨婦，歇斯底里要用她的淚與嗚咽去吞噬所有。他看見有人在架水泵、挖放泵的水洼，有人向壩堤外側鋪又長又寬的塑料布以作臨時水渠，避免泄水沖涮砂質堤壩，遲恒趕緊過去幫著鋪。很快，四臺水泵開始抽吸庫面積水往外吐。他從壩坡爬上來，水如蛇一樣陰冷地已繞上腳根，不遠處，魏昌龍蹲在壩旁一動不動死死盯著邊線水位。遲恒剛想過去，突然想到極度緊張的人，很容易暴躁失控。

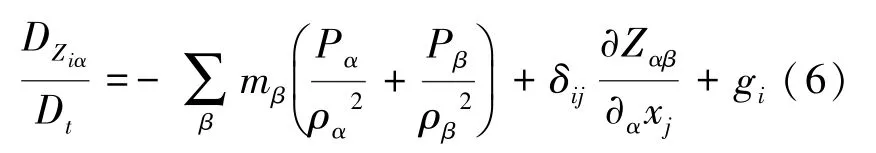
3.1.2 模擬結構的FEM 方程

利用虛功原理建立的非線性動力學有限元控制方程為式(7)：

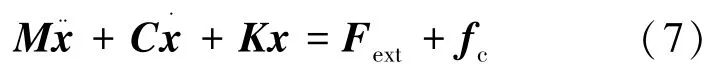
式中，M 為質量矩陣，見式(8)；K 為總體剛度矩陣，見式(9)；Fext為外力矢量，見式(10)；fc為接觸力。

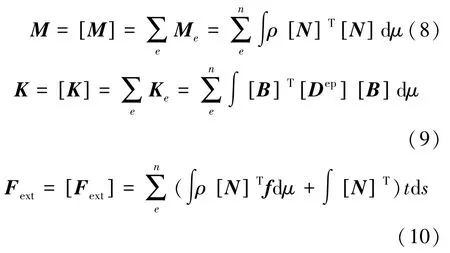
式中，f 為單位質量體力矢量，t 為面力矢量。

3.1.3 SPH-FEM 交界面接觸處理

流體和結構分別采用了基于拉格朗日描述的SPH 方法和FEM 方法求解，因此可方便地通過接觸算法處理流體與固體的交界面。 將SPH 粒子視為從節(jié)點，對應的結構面視為主面，在兩者間建立基于罰函數(shù)方法的通用接觸算法。 其原理是在每一時間步首先搜尋各從點是否穿透其靶點，沒有穿透者不作任何處理；如果穿透，則在該從點和其靶點之間引入1 個較大的法向接觸力，法向接觸力正比于從點相對于其靶點的穿透量和表征接觸碰撞界面剛度的罰因子，從而使穿透部分自動回到平衡位置。 在物理上相當于在從點與靶點之間放置一法向彈簧，以限制兩者之間的穿透。

3.2 建模過程

用Radioss 有限元軟件建立了洗衣裝置洗滌過程的仿真模型，見圖3。 模型中柔性袋內內容物會發(fā)生大變形，因此將其離散為SPH 粒子，其余部分離散為有限單元。 為簡化計算，柔性袋內內容物不額外區(qū)分衣物和水，而是根據總體積離散為均勻密度的SPH 粒子。 SPH 粒子總體積為柔性袋容量的50%，等效為含水率300%的1 kg棉質衣物，由于微重力下衣物會懸浮于包內，故將粒子分布于柔性袋中央位置，粒子間隙為4 mm，粒子總數(shù)為11.9667 萬。 洗衣裝置結構尺寸如表1所示，柔性袋與凸包都為薄壁件，離散為殼單元，單元尺寸為4 mm 左右。 因凸包變形小且不受關注，為減少計算量，用RB2 單元將其剛化。 凸包與柔性袋單側過盈量為5 mm。 模型中SPH 粒子分別與PP 框架、硅橡膠片建立接觸連接，PP 框架單元與硅橡膠單元通過共節(jié)點連接，硅橡膠片分別與前凸包、后凸包建立接觸連接。 仿真模型中各材料屬性如表2 所示。

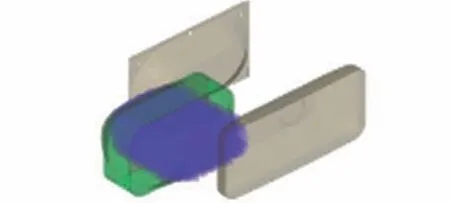
圖3 仿真模型圖Fig.3 Simulation model

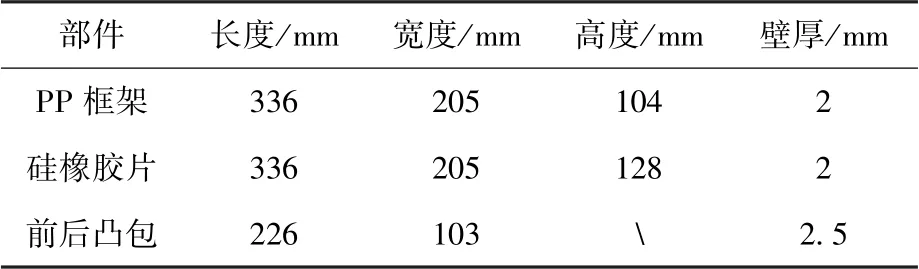
表1 洗衣裝置結構尺寸Table 1 Dimensions of the washing device

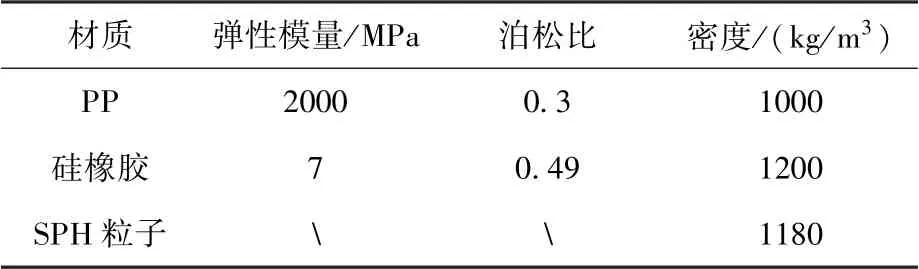
表2 仿真模型材料屬性Table 2 Material features of the simulation model

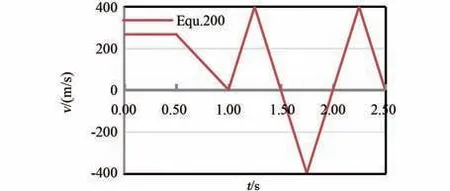
圖4 洗滌包速度控制圖Equ.200Fig.4 The controlled velocity figure Equ.200 of washing bag

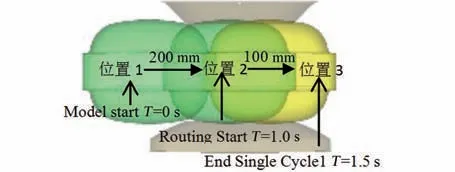
圖5 洗滌包運動軌跡Fig.5 Movement locus of the washing bag

3.3 仿真結果

基于上文仿真模型可獲取SPH 粒子和洗衣裝置接觸力以及粒子速度云圖，其中粒子接觸力可作為洗衣過程中機械力評價指標，粒子速度可作為洗衣過程中衣物翻滾評價指標。 圖6 為仿真過程中， SPH 粒子與柔性袋PP 框架間、SPH 粒子與柔性袋橡膠片間、柔性袋橡膠片與凸包間的法向接觸力合力隨時間變化曲線圖。 可以看出，代表衣物的SPH 粒子與柔性袋PP 框架間，不發(fā)生撞擊時，作用力為0；發(fā)生撞擊時會產生峰值應力，其中在第2 和第3 個單向行程中，各有一次撞擊，分別產生130 N 與156 N 的峰值應力。 代表衣物的SPH 粒子與橡膠片間的作用力，在衣物撞擊PP 框架前，就已開始增大，并在撞擊時達到峰值49.2 N 與89.1 N。 這表明撞擊前SPH 粒子在一端聚集，聚集的SPH 粒子受到凸包的擠壓，使得接觸力開始增大，撞擊PP 框架后粒子散開來，在凸包擠壓作用與粒子撞擊橡膠片的共同作用下，使得接觸力達到峰值。 凸包對橡膠片的擠壓力，穩(wěn)定在17.6 N，在SPH 粒子與PP 框架撞擊前后時，因粒子聚集，擠壓力增大。

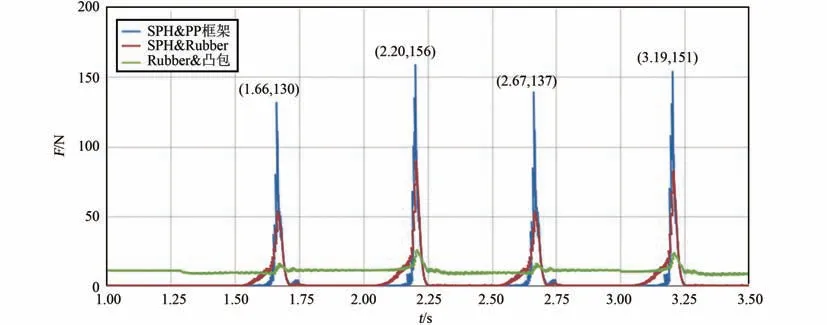
圖6 接觸力與時間曲線圖Fig.6 The normal contact force over time

圖7 為SPH 粒子撞擊柔性袋時模型的x 方向速度云圖，圖7(a)為t ＝1.66 s 時刻，即第一次撞擊時的情形。 此時柔性袋速度為沿x 負方向，靠右端與柔性袋接觸的粒子，速度已變?yōu)檠豿 正向，靠左端大部分粒子仍具有沿x 正向的速度。粒子的這一速度變化過程可代表此時衣物有1 個翻轉運動過程。 類似圖7(b)為t＝2.2 s 時刻第2次撞擊時的情形，此時也代表衣物有一個翻轉運動過程。

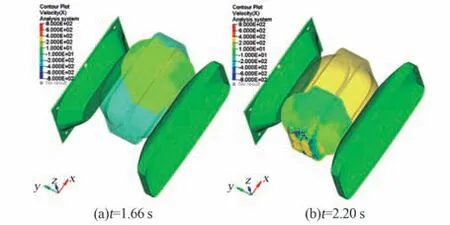
圖7 SPH 粒子撞擊PP 框架時速度云圖Fig.7 The velocity contour plot when SPH particles hit PP Frame

根據式(1)可計算初版裝置洗凈參數(shù)I1＝f1·n1·m1·j1＝94.2，其中機械力f1＝(130+156+49.2+89.1)/2 ＝212.15 N，n1＝2/3，m1＝2/3，j1＝1。同樣可計算滾筒洗衣機洗凈參數(shù)：以內桶直徑D＝500 mm 滾筒洗衣機為參考，2 kg 重物提升至桶內最高點，然后自由落體，取沖擊時間為15 ms，由動量定理mv＝ft 得出沖擊力為417 N，即有fbase＝417 N，nbase＝1，mbase＝1，jbase＝1，得出Ibase＝417。由于初版裝置洗凈參數(shù)I1＜Ibase，因此需對當前系統(tǒng)進行優(yōu)化，提高裝置的洗凈能力。

4 仿真優(yōu)化

為提升洗滌裝置的洗凈能力，本文從柔性包速度和凸包凸臺結構2 方面進行優(yōu)化。

4.1 速度參數(shù)優(yōu)化

建立了速度優(yōu)化模型，與原模型相比，僅PP框架的x 方向速度約束更改為圖8(0.25～1.25 s洗滌包的平均速度為400 mm/s，故下文均以圖Equ.400 表示)。 圖9～11 分別為優(yōu)化前后的結果對比圖，且將優(yōu)化后結果的時間軸數(shù)值放大了1倍。 對比圖9 中SPH 粒子與PP 框架接觸力可知，第1 次撞擊的峰值應力由130 N 提升為379 N，第2 次撞擊峰值應力由156 N 提升為520 N，撞擊力度提升了約3 倍。 對比圖10 中SPH 粒子與橡膠片間的接觸力，可知峰值接觸力分別為160 N 與300 N。 結合圖11 中凸包與橡膠片間的接觸力，可知凸包過盈擠壓時的穩(wěn)定接觸力沒變，此時凸包對衣物擠壓力的增大主要來自于撞擊時速度的提升。 綜合而言，同等情況下，速度提升1 倍，衣物撞擊PP 框架時，整個柔性袋傳遞給衣物的峰值力提升了約3 倍，撞擊頻率與翻轉頻率沒變。 據分析結果有f ＝(379+520+160+300)/2 ＝679.5，n ＝2/3，m＝2/3，J ＝1，計算得I2＝302。 比較得I1＜I2＜Ibase，即速度優(yōu)化后，洗凈能力有提升，但仍沒達到當前滾筒洗衣機標準。

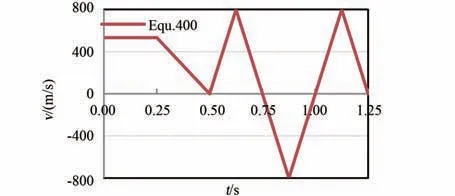
圖8 洗滌包速度控制圖Equ.400Fig.8 The controlled velocity figure Equ.400 of washing bag

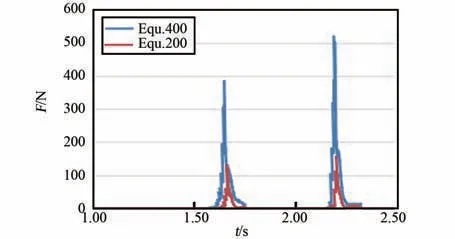
圖9 SPH 粒子與PP 框架接觸力Fig.9 The contact force over time between SPH partials and PP frame

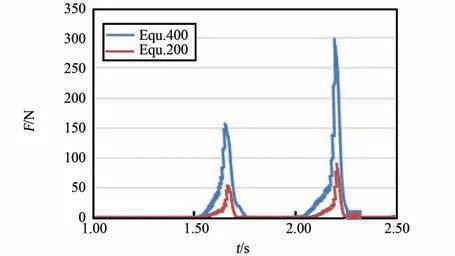
圖10 SPH 粒子與橡膠片接觸力Fig.10 The contact force over time between SPH partials and rubber sheet

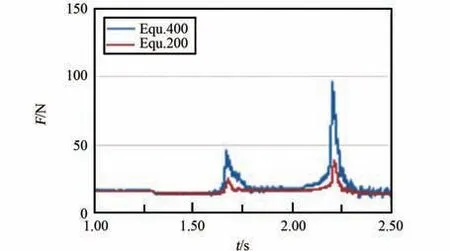
圖11 凸包與橡膠片接觸力Fig.11 The contact force over time between bumps and rubber sheet

4.2 凸包凸臺結構優(yōu)化

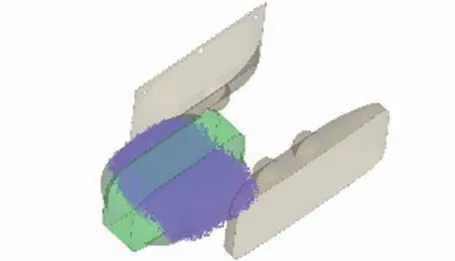
圖12 凸包凸臺結構優(yōu)化模型Fig.12 The simulation model with bumps structure optimized

在4.1 基礎上繼續(xù)優(yōu)化，將原凸包優(yōu)化為圖12中的結構，即在原凸包上增加高為30 mm 的凸臺。前后凸包上的凸臺交叉分布，分別為1 個和2 個。圖13～15 為更改前無凸臺結構與更改后有凸臺結構的仿真結果對比圖。 圖13 顯示有凸臺時，在第2個單向行程中，SPH 粒子與橡膠片有2 次(t ＝0.81 s、t ＝0.86 s)連續(xù)撞擊，分別產生峰值162 N 與78.1 N 的峰值力；第3 個單向行程2 次連續(xù)撞擊(t＝1.07 s、t＝1.11 s)分別產生361 N與97.7 N 的峰值力。 對比無凸臺結構仿真結果，撞擊產生的峰值力下降，撞擊頻率提升1 倍。 圖14 為SPH 粒子與PP 框架間的接觸力，結果顯示，有凸臺時，每次撞擊前后，高擠壓力作用的時間會明顯增長。 圖15解釋了橡膠片與凸包接觸力隨時間的變化關系，因前后凸包上凸臺間隔作用，橡膠片受到約80 N 的擠壓力且時間較長，一旦SPH 粒子聚集，橡膠片受到的擠壓力就會傳遞給SPH 粒子，且將聚集的SPH 粒子擠散，這很好地解釋了橡膠片與SPH 粒子間高擠壓力作用時間長的原因。 圖16 顯示了SPH 粒子撞擊PP 框架時模型的速度云圖，查看圖中柔性袋與粒子的變化形態(tài)，以及粒子速度分布，可知有凸臺后，衣物易被展開，翻轉效率提升0.5倍。 綜合而言，增加凸臺后，衣物撞擊PP 框架時，整個柔性袋給衣物的峰值力下降約1 倍，撞擊頻率提升1 倍，凸臺易于將團起的衣物展開，衣物翻轉效率提升0.5 倍。 據分析結果有f ＝(162+78.1+361+97.7+80×4)/4 ＝254.7，n ＝4/3，m ＝4/3，J ＝3/2，計算得I3＝679.2。 比較得I3＞Ibase＞I2，即同時進行速度優(yōu)化與結構優(yōu)化后，洗凈達到了當前滾筒洗衣機標準。

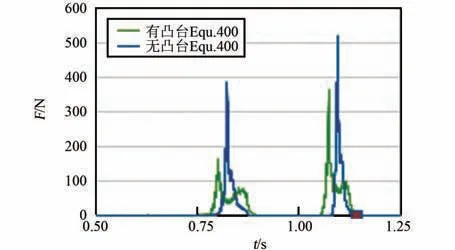
圖13 SPH 粒子與橡膠片接觸力Fig.13 The contact force over time between SPHpartials and rubber sheet

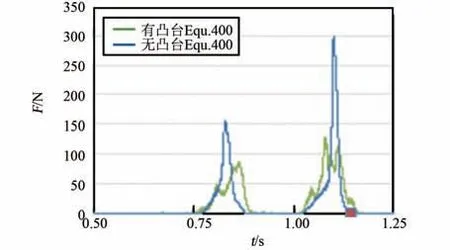
圖14 SPH 粒子與PP 框架接觸力Fig.14 The contact force over time between SPH partials and PP frame

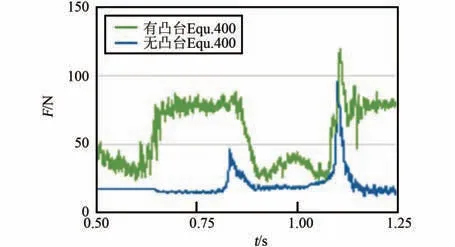
圖15 橡膠片與凸包接觸力Fig.15 The contact force over time between rubber sheet and bumps

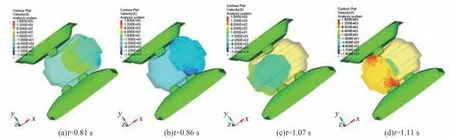
圖16 SPH 粒子撞擊PP 框架時速度云圖Fig.16 The velocity contour plot when SPH particles hit PP Frame

4.3 情形對比

柔性袋內內容物容量不同時，洗凈能力會有差異。 因此建立了內容物占柔性袋96%容量時的模型如圖17，以衡量接近滿負載狀況下，所設計洗衣裝置的洗凈能力。 圖18～20 為同等條件下，50%與96%內容物仿真結果對比圖。 圖18 顯示，內容物增加到96%后，由于柔性袋內空隙小，撞擊次數(shù)增加，每個單向行程中至少會發(fā)生1 次SPH粒子與PP 框架的撞擊，撞擊峰值力度分別為231.9 N、473.7 N、217.8 N 與286.1 N。 圖19～20顯示，內容物增加到96%后，SPH 粒子一直處于聚集狀態(tài)，沒有足夠的空間展開。 因此，凸包凸臺會持續(xù)擠壓橡膠片，進而擠壓SPH 粒子，每個單向歷程中會持續(xù)受到與峰值力100 N 相當?shù)臄D壓力。結合圖21 第1 個單向行程形態(tài)圖，可知撞擊后粒子速度緩慢變?yōu)?，而不是迅速反向，此時翻轉效率極低。 綜合而言，與50%內容物相比，當柔性袋內有96%內容物時，衣物撞擊PP 框架時，袋內衣物受到的峰值力增大1 倍，撞擊頻率提升0.3 倍，翻轉效率降低0.5 倍。 計算得f ＝(231.9+473.7+217.8+286.1+100×4)/4 ＝402.4，n ＝4/3，m ＝4/3，J＝1/2，I4＝357.7。 I4＝0.86Ibase，表明洗凈沒達到當前滾筒洗衣機標準，需增加約1/5 的洗滌時長。

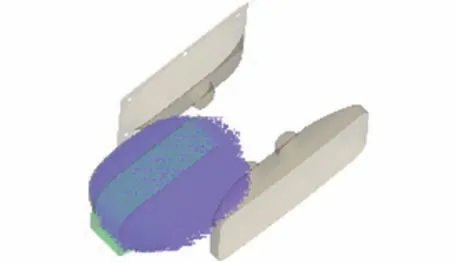
圖17 優(yōu)化后96%內容物模型Fig.17 The simulation model with 96%volume occupied

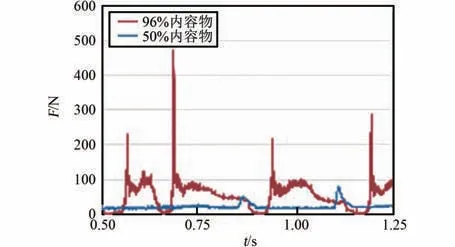
圖18 SPH 粒子與PP 框架觸力Fig.18 The contact force over time between SPH partials and PP frame

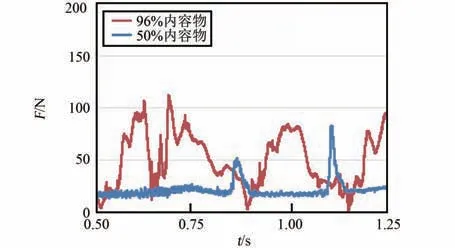
圖19 SPH 粒子與橡膠片接觸力Fig.19 The contact force over time between SPH partials and rubber sheet

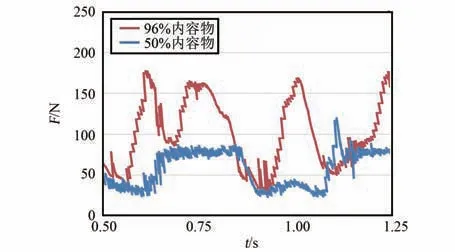
圖20 橡膠片與凸包接觸力Fig.20 The contact force over time between rubber sheet and bumps

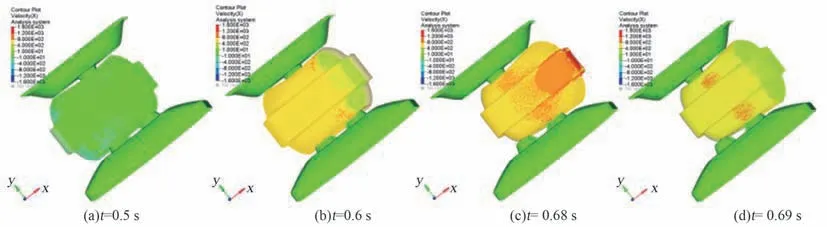
圖21 96%內容物模型第1 個單向歷程中速度云圖Fig.21 The velocity contour plot of 96%volume occupied model during the first single routing

5 結論

1)建立了基于光滑粒子動力學法(SPH)與有限元法(FEM)耦合的流固耦合模型，獲取了SPH 粒子和洗衣裝置接觸力以及粒子速度云圖，粒子接觸力作為洗衣過程中機械力評價指標，粒子速度作為洗衣過程中衣物翻滾評價指標。

2)柔性袋速度提升和凸包增加凸臺結構均能增大洗滌過程機械力。 柔性袋速度提升1 倍，同時擠壓凸包增加凸臺結構，在50%負載工況下裝置能達到當前滾筒洗衣機相近的洗凈度。

3)洗滌衣物量影響洗衣裝置洗凈能力，可通過增加洗滌時長相應提升洗凈能力。

參考文獻(References)

[1]強洪夫.光滑粒子流體動力學新方法及應用[M].北京：科學出版社，2017：20-49.Qiang H F.New Method and Application of Smoothed Particle Hydro-dynamics[M].Beijing： Science Press， 2017： 20-49.(in Chinese)

[2]王勖成.有限單元法[M].北京：清華大學出版社，2003：468-520.Wang X C.Finite Element Method[M].Beijing： Tshinghua University Press， 2003： 468-520.(in Chinese)

[3]Attaway S W，Heinstein W M，Mello F J，et al.Coupling of smooth particle hydro-dynamics with PRONTO[C]/ /1993 ASME Winter Annual Meeting，New Orleans，1993.

[4]Attaway S W，Heinstein W M，Mello F J.Coupling of smooth particle hydrodynamics with finite element method [J].Nuclear Engineering and Design，1994，150：199-205.

[5]Sonia F，Javier B，Antonio H.Continuous blending of SPH with finite elements[J].Computer ＆ Structures，2005，83：1448-1458.

[6]馬利，陶偉明，郭乙木， 等.SPH 耦合有限元方法的水射流彈塑性碰撞模擬[J].浙江大學學報，2008，42(2)：259-263.Ma L， Tao W M， Guo Y M，et al.Elastic/plastic impact simulation of water jet using smoothed particle hydrodynamics and finite element method[J].Journal of Zhejiang University，2008， 42(2)： 259-263.(in Chinese)

[7]肖毅華，韓旭，胡德安.流體與結構相互作用問題的FESPH 耦合模擬[J].應用力學學報，2011，28(1)：13-18.Xiao Y H， Han X， Hu D A.FE-SPH coupling simulation of fluid-structure interaction problems[J].Chinese Journal of Applied Mechanics， 2011， 28(1)： 13-18.(in Chinese)

[8]孫芳錦，張大明.基于光滑粒子流體動力學的流固耦合問題研究[J].地震工程與工程振動， 2013， 33(6)： 222-227.Sun F J， Zhang D M.Study on fluid-structure interaction based on smoothed particle hydro-dynamics[J].Journal of Earthquake Engineering and Engineering Vibration，2013，33(6)：222-227.(in Chinese)