捆綁火箭超靜定連接結構參數化建模與優化

蔣國慶，陳萬華，王元興

(中國空氣動力研究與發展中心設備設計及測試技術研究所，綿陽621000)

1 引言

助推器能夠大幅度提高火箭的運載能力，各航天大國相繼在各自的運載火箭系列的基礎上開發出了捆綁式運載火箭[1]。 助推器與火箭芯級之間一般采用靜定式連接，也有采用超靜定連接方式。 超靜定連接結構設計與剛度相關，且在一定程度上影響了火箭的動特性[2]。 為實現火箭結構輕量化，提高火箭運載能力，有必要對超靜定連接結構進行優化設計。

隨著計算機技術和結構優化設計方法的不斷發展，基于參數化模型和智能優化算法的聯合優化方法得到了越來越廣泛的研究和使用[3]。 參數化建模的應用范圍十分廣泛，目前主要研究方向是參數化造型[4]。 主流CAE 軟件的二次開發功能可以實現參數化建模，主要的二次開發工具有ANSYS 的APDL 語言[5]、ABAQUS 的Python語言[6]和MSC.PATRAN 的PCL 語言[7]等。 智能優化算法包括遺傳算法、模擬退火算法等，其中遺傳算法是模仿自然界生物進化機制而發展起來的隨機全局搜索和優化方法[8-9]，使用尤其廣泛。 本文采用PCL 語言建立捆綁火箭超靜定連接結構的參數化模型，并結合遺傳算法對其進行優化設計。

2 有限元模型

某捆綁火箭主要由芯級和四個助推器組成，按常規梁單元建模，即以站點為節點，將箭體質量分布在各節點處并在節點處建立相應的質量單元(MASS 單元)，而節點與節點之間則用無質量梁單元連接。 芯級與助推器之間的連接結構對火箭的動特性有重要影響，需要采用合理的方法對其進行模擬。

捆綁連接結構由前捆綁、中捆綁和后捆綁組成，其中前捆綁和中捆綁均采用大剛度梁單元(CBEAM 單元)連接捆綁火箭芯級梁、助推器中心梁梁上和箭體周邊的連接點，以此模擬火箭連接處的剛性面，采用桿單元(CROD 單元)模擬芯級與助推器之間的連桿，同時利用CBEAM 單元和CROD 單元之間自由度的不匹配關系來模擬連桿端點處的鉸接效果。 后捆綁連接處為一球鉸，在此采用RBE2 單元進行模擬，釋放其3 個轉動自由度。 這樣助推器與芯級之間形成超靜定結構，且每個助推器與芯級之間均為一次超靜定。

超靜定捆綁火箭梁模型及其三維顯示圖如圖1 所示。

3 參數化建模

圖1 捆綁火箭梁模型及其三維顯示圖Fig.1 Beam model and its 3D display of strap-on launch vehicle

火箭的捆綁連接結構比較復雜，且質量較重，通過對其進行優化設計可以減輕重量。 采用遺傳算法對捆綁連接結構進行優化設計前，需要得到捆綁連接結構的參數化模型。

3.1 參數選取

根據獨立性原則和完備性原則，設置優化參數見表1，各參數位置見圖2。

表1 捆綁連接結構選用參數統計表Table 1 Main parameters of connection structure

3.2 參數化建模

在創建火箭有限元梁模型的過程中，軟件會自動生成記錄歷史建模命令的model＿name.db.jou文件。 提取該文件中的建模命令并把預先設定的參數或參數表達式代替相應建模命令中的數據，即可得到捆綁火箭的參數化模型。

4 結構優化設計

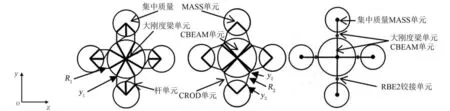
圖2 捆綁火箭捆綁連接結構Fig.2 Connection structure of strap-on launch vehicle

對火箭中的超靜定連接結構進行優化設計時，把設計變量設置為各連桿的位置坐標及各連桿的外徑；考慮到火箭第一階自振頻率對火箭動特性的重要性，在此把性能約束條件設置為火箭第一階自振頻率要求不能低于某一數值；考慮到加工可行性和結構協調性，在此把幾何約束條件設置為各連桿的位置坐標和各連桿的外徑只能在一定范圍內變動。 從而，捆綁火箭連接件的優化模型可以描述為式(1)：

優化設計方法有多種，如傳統的線性規劃法、無約束優化方法、約束優化方法、離散設計變量優化方法等。 本次優化設計中各連桿的具體坐標和各連桿的外徑與火箭的動特性(如自振頻率等)之間的關系很復雜，無法推導出其顯示表達式，因此難以采用傳統優化算法解決此問題。 而啟發式算法如遺傳算法、模擬退化算法等能夠很好得解決此問題。 本文采用遺傳算法對捆綁連接結構進行優化設計，計算流程[4]如圖3 所示。

本次優化設計中捆綁連接結構5 個參數的變化范圍如表2 所示。 遺傳算法的運行參數設置為群體規模為60，迭代次數為40，基于MATLAB、MSC.PATRAN 以及MSC.NASTRAN 的聯合優化設計流程如圖4 所示。

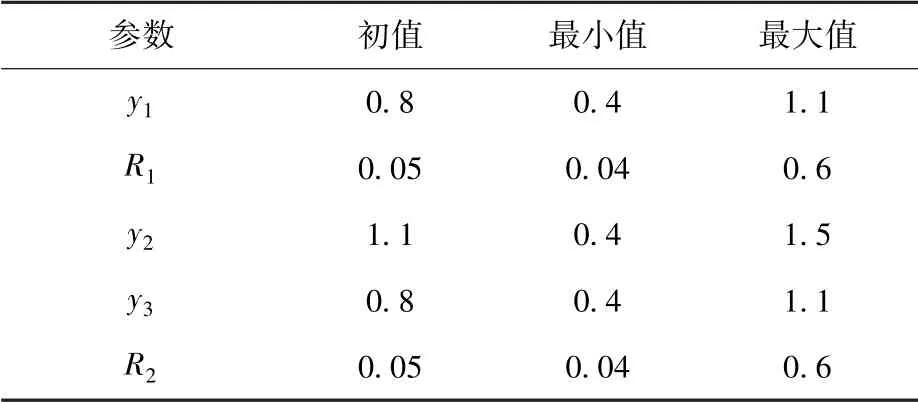
表2 各參數變化范圍Table 2 Range of parameters/m

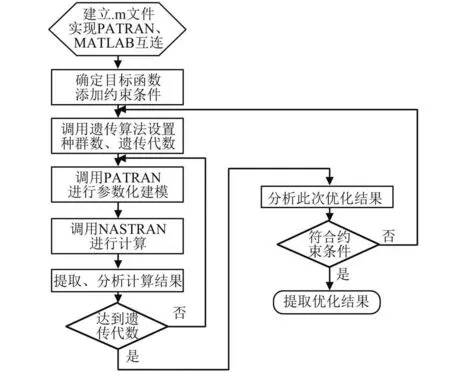
圖4 捆綁火箭連接件優化設計流程Fig.4 Optimization process of connection structure

遺傳算法的計算歷程如圖5 所示。 由圖可知，連桿總質量隨著迭代次數的增加，先急劇下降，后變得非常平緩，說明此次優化設計收斂性較好，連桿總質量在第40 代時得到了最優值。 各參數的優化結果如表3 所示。 優化后火箭前捆綁、中捆綁連接形式如圖6 所示。 由表3 和圖6 可知，優化后模擬火箭剛性面的大剛度梁單元之間的夾角明顯減小，同時前捆綁和中捆綁連桿外徑均有所減小。

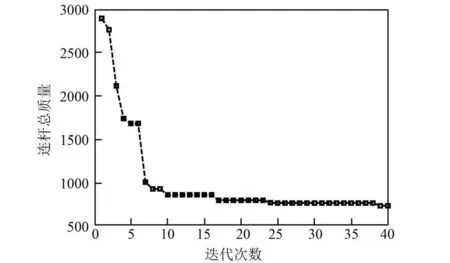
圖5 遺傳算法的迭代計算過程Fig.5 Iterative computation process of GA

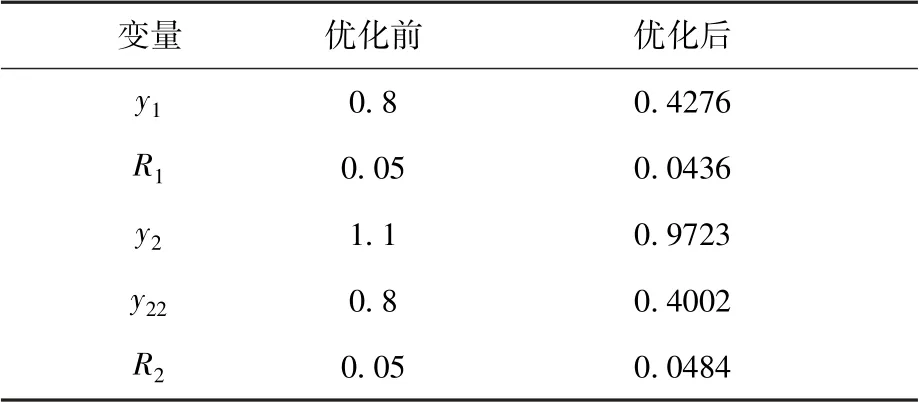
表3 優化前后各設計變量數值對比表Table 3 Comparison of variables before and after optimization/m

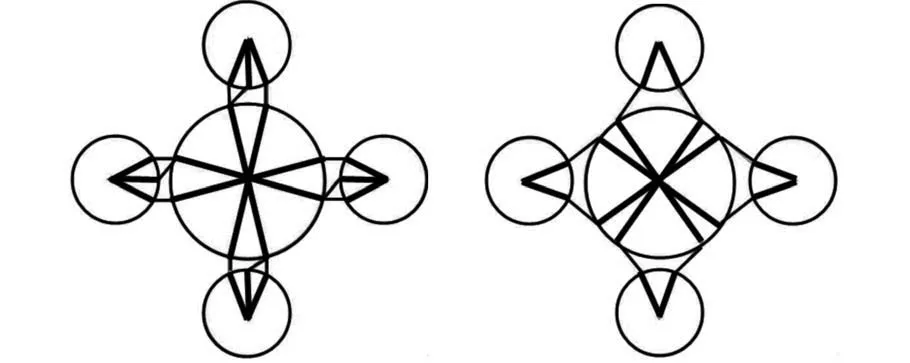
圖6 優化后前、中捆綁連接結構示意圖Fig.6 Schematic diagram of main connection structure after optimization

優化后連桿總質量及捆綁火箭第一階自振頻率如表4 所示。

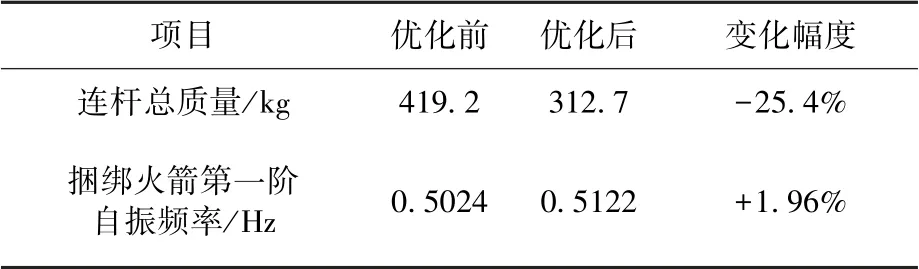
表4 優化前后連桿總質量和捆綁火箭第一階自振頻率對比表Table 4 Comparison of total quality and first order frequency before and after optimization

由表4 可知，優化后連桿總質量比優化前連桿總質量減少了25.4%，主要是由兩個方面造成：①連桿位置的改變導致了連桿長度的縮短；②前捆綁、中捆綁連桿的外徑分別減少了12.8%、3.2%。 優化后捆綁火箭的第一階自振頻率比優化前只上升了1.96%，這主要是由于連桿總質量在捆綁火箭總質量中所占的比重較小。 綜上可知，優化后，捆綁火箭的彎曲基頻有所增加，捆綁火箭連桿總質量降幅顯著，達到了預期目的。 但評論本次優化結果的有效性還需比較優化前后火箭動特性和連桿內力。

5 優化前后捆綁火箭對比

5.1 優化前后動特性分析

對優化前后捆綁火箭分別進行自由狀態下的模態分析，得到第一階彎曲和第一階扭轉模態及所對應的自振頻率對比如表5 所示。

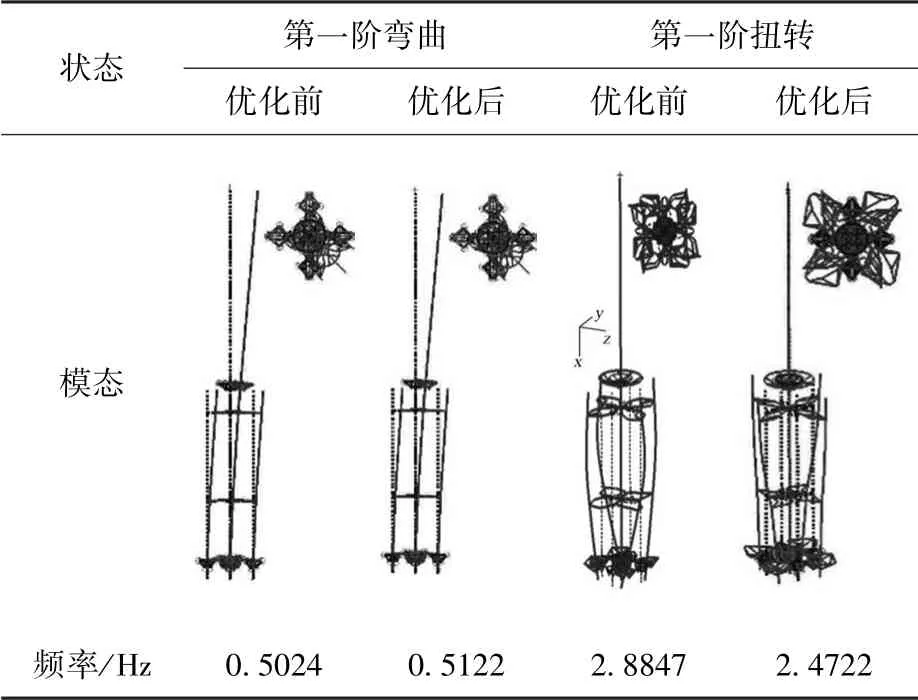
表5 優化前后捆綁火箭自振頻率和模態對比表Table 5 Comparison of frequency and modes before and after optimization

由表5 可知，優化后的扭轉基頻比優化前降低了14.3%。 說明在保持連桿數量和連桿連接方式的前提下，連桿的位置和連桿的外徑使得捆綁火箭的扭轉基頻變化較大，而對捆綁火箭的彎曲基頻影響不大。

5.2 優化前后捆綁火箭連桿載荷分析

捆綁火箭起飛前豎立在發射臺上，只受重力作用，邊界條件為火箭芯級底部固支。 此種工況下優化前后捆綁火箭連桿最大內力及后捆綁主接頭各向最大節點力對比表如表6 所示。

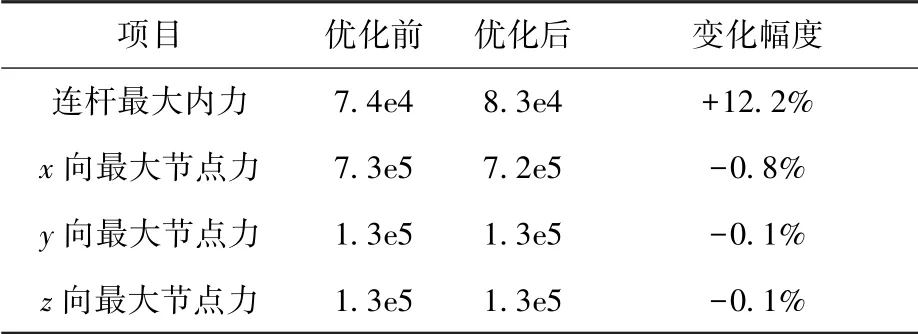
表6 優化前后捆綁火箭連桿載荷對比表Table 6 Comparison of load in connective rods before and after optimization/N

由表6 可知，優化后連桿的最大內力較優化前增加較多，這主要是由于優化后連桿位置發生變化所致。 優化前后捆綁火箭后捆綁主接頭的各向最大節點力相差不大，部分方向的節點力得到了改善。

綜上可知，優化后捆綁火箭的動特性和連桿載荷情況都有了一定的改善。

6 結論

1)利用CBEAM 單元和CROD 單元之間自由度的不匹配關系能夠很好得模擬連桿端點處的鉸接效果。

2)采用PCL 語言和遺傳算法能夠對捆綁火箭超靜定連接結構進行優化設計，且優化效果比較明顯，其中連桿總質量減小了25.4%，火箭彎曲基頻基本保持不變，火箭扭轉基頻減小了14.3%，連桿所受載荷得到一定改善。

參考文獻(References)

[1]康開華，才滿瑞，尚輝.質子號運載火箭及其運營[J].導彈與航天運載技術， 2006， 3(283)： 21-27.Kang K H，Cai M R，Shang H.Proton launch vehicles and its operation[J].Missile and Space Vehicle，2006，3(283)：21-27.(in Chinese)

[2]李家文.大型捆綁火箭姿態控制系統的建模、設計與分析[D].長沙： 國防科學技術大學， 2011.Li J W.Modeling， Design and Analysis of Large Strap-on Vehicle's Attitude Control System[D].Changsha： National University of Defense Technology， 2011.(in Chinese)

[3]麻越垠，陳萬華，王元興，等.基于響應面方法的葉柵擺動裝置有限元模型修正[J].振動與沖擊， 2016， 35(22)：232-236.Ma Y Y， Chen W H， Wang Y X， et al.Finite element model updating of the blade swing mechanism based on response surface method [J].Journal of Vibration and Shock， 2016， 35(22)： 232-236.(in Chinese)

[4]李磊.基于結構完整性分析的固體火箭發動機藥形改進與優化設計[D].長沙： 國防科學技術大學， 2011.Li L.Improvement and Optimization Design of Solid Rocket Motor based on Structural Integrity Analysis[D].Changsha：National University of Defense Technology， 2011.(in Chinese)

[5]師訪.ANSYS 二次開發及應用實例詳解[M].北京： 中國水利水電出版社， 2012： 17-34.Shi F.Second Development and Application Example of ANSYS[M].Beijing： China Water ＆ Power Press， 2012： 17-34.(in Chinese)

[6]蘇景鶴， 江丙云.ABAQUS Python 二次開發攻略[M].北京： 人民郵電出版社， 2016： 12-14.Su J H， Jiang B Y.Second Development Strategy of ABAQUS Python[M].Beijing： Posts ＆ Telecom Press， 2016： 12-14.(in Chinese)

[7]李磊， 唐國金， 段靜波， 等.基于參數化建模的車輪形藥柱形狀優化[J].國防科技大學學報， 2011， 33(1)： 11-16.Li L， Tang G J， Duan J B， et al.Shape optimization of wheel shape grain based on parameterized modeling[J].Journal of National University of Defense Technology， 2011， 33(1)：11-16.(in Chinese)

[8]劉翔春， 廖瑛， 文援蘭.應用改進遺傳算法優化天基光學監視平臺軌道[J].國防科技大學學報，2014，36(3)：58-62.Liu X C， Liao Y， Wen Y L.Applying the improved genetic algorithm to optimize the orbit for space-based optics surveillance platform[J].Journal of National University of Defense Technology， 2014， 36(3)： 58-62.(in Chinese)

[9]宋春生， 于傳超， 張錦光， 等.基于遺傳算法的復雜雙層磁懸浮精密隔振系統LQR 控制研究[J].振動與沖擊，2016， 35(16)： 99-105.Song C S， Yu C C， Zhang J G， et al.LQR Control of a Complex Two-stage Magnetic Suspension Active Precise Isolation System based on Genetic Algorithm[M].Journal of Vibration and Shock， 2016， 35(16)： 99-105.(in Chinese)