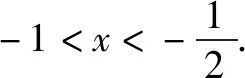抽象函數(shù)問題的教學(xué)反思

陳廣義

(內(nèi)蒙古鄂爾多斯市鄂托克旗高級(jí)中學(xué) 016100)

抽象函數(shù)定義域問題一直是學(xué)生學(xué)習(xí)的難點(diǎn)，如何行之有效地解決此類問題是值得我們反思的.我所在的學(xué)校是基層學(xué)校，學(xué)生基礎(chǔ)比較差，如何在符合學(xué)情的情況下讓學(xué)生理解并掌握抽象函數(shù)定義域問題呢？我是這樣設(shè)計(jì)的：

問題1(2018·青島一模)已知函數(shù)f(x)的定義域?yàn)?-1,0)，則函數(shù)f(2x+1)的定義域是____.

設(shè)計(jì)目的：由學(xué)生討論并總結(jié)一般規(guī)律，符合特殊到一般認(rèn)識(shí)規(guī)律.

甲同學(xué)：由已知得-1

再經(jīng)過討論，大家認(rèn)可乙同學(xué)答案.盡管學(xué)生聽懂了的解法，但是似乎理解上依然存在困惑.抽象函數(shù)通常指一類沒有給出具體解析式的函數(shù),其概念是非常簡(jiǎn)單的形式定義,學(xué)生理解有相當(dāng)難度,很難準(zhǔn)確揭示概念的本質(zhì)屬性.為了讓學(xué)生了解數(shù)學(xué)本質(zhì)，我們還要回歸函數(shù)的概念.一般地,設(shè)A、B是非空的數(shù)集,如果按照某種確定的對(duì)應(yīng)關(guān)系f,使對(duì)于集合A中的每一個(gè)數(shù)x,在集合B中都有唯一確定的數(shù)f(x)和它對(duì)應(yīng),那么就稱f:A→B為集合A到集合B的一個(gè)函數(shù),其中x叫做自變量,x的取值范圍也就是集合A叫做函數(shù)的定義域.因此任何函數(shù)的定義域都是指自變量x的取值范圍.正是由于定義域中自變量x的首先變化，引起了函數(shù)值的變化，所以，函數(shù)的定義域確切地說是函數(shù)中首先變化的那個(gè)量的所有取值組成的集合.通過老師引導(dǎo)和學(xué)生討論.

追問：同學(xué)們回答都很好，哪位同學(xué)總結(jié)一下已知f(x)的定義域是[a，b]，求f(g(x))的定義域過程.

丁同學(xué)：可通過a≤g(x)≤b，求出x的取值范圍.

設(shè)計(jì)意圖:已知f(g(x))的定義域是[a，b]，求f(x)的定義域.

為了更好理解，我又引入一道題，希望在教學(xué)中可將抽象問題具體化，這樣更符合學(xué)生的思維發(fā)展過程.把求抽象函數(shù)定義域問題轉(zhuǎn)化求函數(shù)解析式問題中解決.

問題3：已知函數(shù)f(x2-1)=x4-2x2-1，求函數(shù)f(x)的解析式和定義域.

設(shè)計(jì)意圖:抽象問題具體化,便于學(xué)生理解.

解(配湊法)：∵x4-2x2-1=(x2-1)2-2，∴f(x2-1)=(x2-1)2-2，x2-1≥-1，即f(t)=t2-2，t≥-1.故f(x)=x2-1，x≥-1.

點(diǎn)評(píng)函數(shù)f(x2-1)=x4-2x2-1的定義域是(-∞,+∞)，t=x2-1的范圍是[-1,+∞)，而函數(shù)f(x)=x2-1中的x相當(dāng)于函數(shù)f(x2-1)=x4-2x2-1中的x2-1，所以x的范圍是[-1,+∞)，即定義域是[-1,+∞).

追問：把題目變式為“已知函數(shù)f(x2-1)的定義域?yàn)?-∞,+∞)，求函數(shù)f(x)的定義域.”有了上面有具體解析式的函數(shù)的鋪墊，學(xué)生隨口而出.

接著在解決問題二就相對(duì)容易了，讓學(xué)生板演.

問題4:題1改為求函數(shù)g(x)=f(2x+1)+f(3x+1)的定義域．

設(shè)計(jì)意圖:抽象函數(shù)定義域問題逐步滲透，加深對(duì)函數(shù)的理解與應(yīng)用.

追問：同學(xué)們作的都很好，哪位同學(xué)總結(jié)一下已知f(g(x))的定義域是[a，b]，求f(x)的定義域過程？

戊同學(xué)：可由x∈[a，b]，求g(x)的范圍(即y=g(x)的值域).

反思：老師在課堂上一味地灌輸，學(xué)生死記硬背.這種“填鴨式”的教學(xué)與“機(jī)械模仿式”的練習(xí)，顯然學(xué)生的能力是不可能提高的.要改變這種狀況，教師就需要改進(jìn)教學(xué)方法，努力實(shí)行啟發(fā)式教學(xué)法、自主探究式教學(xué)法、生成性教學(xué)法、問題教學(xué)法、數(shù)學(xué)實(shí)驗(yàn)教學(xué)法、數(shù)學(xué)變式教學(xué)法、情景教學(xué)法等.只有靈活多變的教學(xué)方法才能充分調(diào)動(dòng)學(xué)生的積極性.在教學(xué)過程中作為一線老師就要以學(xué)生為本，注重學(xué)生的思維發(fā)展，能力的培養(yǎng)，從多角度挖掘教材，最大限度地開發(fā)學(xué)生思維.只有這樣師生才能變被動(dòng)為主動(dòng)，才能看到課堂上的共贏.