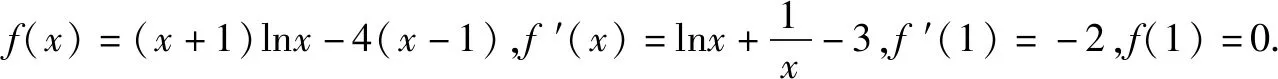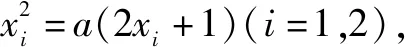不用分離參數法巧解2018年高考全國卷Ⅱ文科數學第21題

甘志國

(北京市豐臺二中 100071)

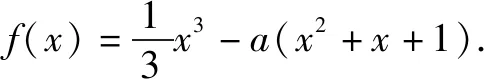
(1)若a=3，求f(x)的單調區間；

(2)證明：f(x)只有一個零點．

參考答案:(1)略．

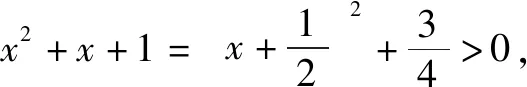
因而g(x)至多有一個零點，即f(x)至多有一個零點．

筆者的注記我們知道，由三次函數的圖象可知“當x→-時f(x)→-，當x→+時f(x)→+”，所以f(x)只有一個零點．但這不能代替嚴格證明，下面這道高考題即題2第(3)問的解答也是這樣的：

題2(2018年高考天津卷文科第20題)設函數f(x)=(x-t1)(x-t2)(x-t3),其中t1,t2,t3∈R，且t1,t2,t3是公差為d的等差數列.

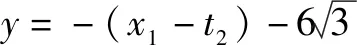
所以題1(2)的參考答案給出了具體實例“f(3a-1)<0,f(3a=1)>0”，但老師應當講清其來源.

x2-3ax-3a>0 ①,

為了簡便，選x=3a+1,可使①式成立，由此便得f(3a+1)>0的來歷.

x2+3ax+3a>0 ②.

因為拋物線y=x2+3ax+3a向口向上，所以存在負數x使得不等式②恒成立，進而可試驗出f(3a-1)<0,這就是f(3a-1)<0的來歷.

以上題1(2)的參考答案給的方法是分離參數法，但考生有這樣的經驗:對于高考壓軸題(導數的應用)，分離參數法往往不湊效，比如下面的題3和題4.

題3(2006年高考全國卷Ⅱ理科第20題)設函數f(x)=(x+1)ln(x+1).若對所有的x≥0，都有f(x)≥ax成立，求實數a的取值范圍.

分析本題的自然想法當然是分離參數法.

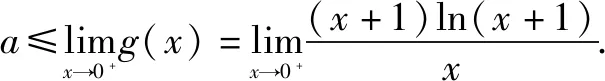
本題的正確解法是不用分離參數法，而是對參數進行分類討論，這種討論的原則是“先充分后必要”.

設g(x)=f(x)-ax=(x+1)ln(x+1)-ax(x≥0)，得題設即g(x)≥g(0)(x≥0)恒成立.

所以當g(x)(x≥0)是增函數即g′(x)≥0(x≥0)恒成立時滿足題設.

可得g′(x)=ln(x+1)+1-a(x≥0)，且g′(x)(x≥0)是增函數，所以當g′(0)=1-a≥0即a≤1時滿足題設.

當a>1時，得g′(x)的零點為ea-1-1，且當x∈(0,ea-1-1)時，g′(x)<0，即g′(x)在(0,ea-1-1)上是減函數，得g(x)

題4 (2016年高考全國卷Ⅱ文科第20題)已知函數f(x)=(x+1)lnx-a(x-1).

(1)當a=4時，求曲線y=f(x)在(1,f(1))處的切線方程；

(2)若當x∈(1,+)時，f(x)>0，求a的取值范圍.

解(1)函數f(x)的定義域為(0，+∞)．

當a≤2時，可得f′(x)>f′(1)=2-a>0(x>1)，所以f(x)是增函數，得f(x)>f(1)=0(x>1)，得此時滿足題意.

當a>2時，可得f′(1)=2-a<0,f′(ea)>0，所以存在唯一的x0∈(1,ea)使得f′(x0)=0.

再由f′(x)是增函數，得當x∈(1,x0)時f′(x)<0，得此時f(x)是減函數，所以f(x)

綜上所述，可得所求實數a的取值范圍是(-,2].

因而，下面不用分離參數法而用“直接求導+對參數分類討論”的方法來求解題1(2).

題1(2)的另證1 可得f′(x)=x2-2ax-a，其判別式Δ=4a(a+1).

可得3f(x)=x2(x-3a)-3ax-3a.

當x-3a≥1即x≥3a+1時，由x2≥0，可得

3f(x)≥x2-3ax-3a=x(x-3a)-3a.

又當x≥0即x≥max{0,3a+1}時，可得

3f(x)≥x-3a≥1,

f(x)>0.

設x=-t，可得-3f(x)=t2(t+3a)-3at+3a.

當t+3a≥1即t≥1-3a也即x≤3a-1時，由t2≥0，可得-3f(x)≥t2-3at+3a=t(t-3a)+3a,又當t≥max{0,3a+1}即x≤min{0,-3|a|-1}時，可得

-3f(x)≥t+3a≥1,

f(x)<0.

因而f(x)存在零點.

(1)當Δ≤0即-1≤a≤0時，f(x)是增函數，進而可得函數f(x)有且只有一個零點．

得三次函數f(x)的極大值與極小值同號，因而f(x)有且只有一個零點.得欲證結論成立.

題1(2)的另證2 可得f′(x)=x2-2ax-a，其判別式Δ=4a(a+1).

當x>max{1,9|a|}時，可得0

a(x2+x+1)≤|a|(x2+x+1)≤3|a|x2,

-a(x2+x+1)≥-3|a|x2.

a[t2+(1-t)]≥-|a|[t2+(1-t)]≥-|a|t2,

-a[t2+(1-t)]≤|a|t2.

因而f(x)存在零點.又因為“題1 (2)的另證1”中已證得三次函數f(x)的極大值與極小值同號，所以f(x)有且只有一個零點.得欲證結論成立.