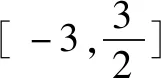導數在高中數學解題中的應用探析
周 曉
(福建省霞浦第一中學 355199)
作為微積分中的基礎知識,導數在研究函數問題和解決實際高中數學難題中發揮著不可忽視的作用.導數通過將函數、方程、向量、數列、不等式、解析幾何等內容有機聯系起來,并為解決這些問題提供了較為統一且能讓學生容易理解和上手的學習方法.根據筆者多年實踐和觀察發現,伴隨著高中新課程改革的不斷深入,導數在高中數學解題方面的作用越來越明顯,地位也越來越特殊,深受學生喜愛.當前,高考考查導數知識角度很多,但萬變不離其宗的是導數與其他數學知識綜合應用能力.比如,導數在解決函數、不等式、切線等實際數學問題中的應用,這不僅要求學生牢牢掌握與導數相關的基礎知識,而且還能夠學以致用,將其運用到解題過程中去.筆者認為,在日常教學活動中,尤其是備考階段,數學教師要幫助學生鞏固導數相關知識,通過模擬練習培養和不斷提高學生利用導數解決實際問題的綜合能力.
一、導數在判斷函數單調性過程中的廣泛應用
眾所周知,函數的單調性是高中數學的主要知識點之一.所謂函數的單調性,指的是在某一區間范圍內,由于自變量發生變化,隨之因變量也會發生變化.一般情況下,判斷函數單調性的依據,我們率先想到的是其具體定義.也就是說,在某一區間范圍內,倘若函數中自變量變大,而因變量隨之變小,則我們稱之為減函數;而倘若函數中自變量變大,因變量也隨之變大,則我們稱之為增函數.其中,相應的區間是其與之對應的單調區間.多年實踐和教學心得發現,這一判斷方式較為滿足且適用于相對簡單的函數單調性.但是,當面臨稍稍復雜的函數時,這一解題思路則會變得顯得過于復雜,同時證明起來相對不易.近年來,伴隨著導數的出現及其在高中數學中的廣泛應用,判斷函數的單調性也變得相對容易起來,不僅快速而且可靠度高,學生也易掌握.通過導數具體判斷某一函數的單調性時,一般做法如下:首先,進行函數在區間范圍內的求導.倘若求導結果>0,那么可以說明的是,此函數在這一區間范圍內,單調呈遞增性質;倘若求導結果<0,則此函數在這一區間范圍內,單調呈遞減性質.筆者認為,若要快速且準確地判斷函數單調性,至關重要的一點是熟練掌握一般函數的求導方式.此外,還要對函數的單調性和函數所對應的區間進行說明.
二、導數在證明不等式過程中的廣泛應用
縱觀近年來高考數學考查內容,筆者發現,考題綜合化及知識的靈活應用成了現階段及未來一段時間內高考命題主要發展趨勢之一.而針對高中數學而言,把不等式相關問題與函數結合起來綜合考查,則成了最為普遍的命題形式之一,很受歡迎.在證明不等式過程中,充分運用導數效果十分明顯,不僅讓考官和教師一目了然,而且相較于以前的解題方式,利用導數解題速度得到了大大的提升.導數在證明不等式過程中的應用一般做法是:將要證明的不等式進行變形,使其變為判斷兩個函數大小的題目;接著構建輔助函數、求出具體導數值;然后再對導數在區間上的正負情況進行判斷,確定其單調性;最后判斷這兩個函數的大小值.此處要引起注意的是,在證明指數函數、對數函數以及三角函數的過程中,通過導數一方面可以有效提高解題的速度,另一方面還能夠引導學生深層次地掌握不等式、方程以及函數等相關知識及其之間的關系,從而加深對其的印象和理解.

證明設AB的中點是P(m,n),那么中點P在橢圓內.
因此,-a 因此,線段AB的垂直平分線斜率滿足: 一直以來,一提及函數求解最值,人們往往會嘆而止步,因為其往往是作為高考難點而出現在考生眼前.針對函數求解最值這一知識點,求解方式可以說是千姿百態.以往的求解方式可以滿足一般函數,但是碰到求解較為復雜的函數最值的時候,考生往往會顯得無從下手,甚至不知所措.此外,更為頭腦的是其解題過程相對不簡單.而導數的出現則大大化解了這一尷尬.舉個例子,我們常見的二次函數求解最值.難點在于,因為二次函數所需要求解的最值是在某一區間范圍的最值,這就要求分別求出這一區間范圍內的最大值抑或是最小值.過去我們遇到這個問題,往往會采取數形互相結合這一方式,而這對于學生而言,解題過程顯得較為繁復冗長,時間成本較大.而通過導數則顯得較為簡單、快捷,一般做法是:通過導數判斷出該函數在區間范圍內的單調性和最大值、最小值,然后對其最值與區間對應關系進行明確,可以說是既高效又快速. 分析第一步:求出f(x)的極值點; 第二步:對比極值點與區間端點函數值; 第三步:求出該函數在區間范圍內的最大值、最小值. 解因為f′(x)=3x2-3=3(x2-1)=3(x+1)(x-1),則 當x∈[-3,-1]或者x∈[1,3/2]時,f′(x)>0,因此[-3,-1],[1,3/2],則是該函數的單調增區間; 當x∈[-1,1]時,f′(x)<0,因此,[-1,1],則是該函數的單調減區間. 由于f(-3)=-18,f(-1)=2,f(1)=-2,f(3/2)=-9/8. 因此,當x=-3的時候,f(x)的最小值為-18; 當x=-1的時候,f(x)的最大值為2. 總的來說,導數在高中數學應用十分廣泛,不僅僅局限于上述所呈現的幾種,方便學生答題解題的同時還在無形中大大提高了對學生的要求.由于導數相關知識點的學習安排在教材末尾,因此在實際解題過程中,學生往往會通過自己慣用的思維來答題,對導數的應用不多.筆者認為,在日常模擬考試及學習過程中,高中數學教師可以適當增加導數相關內容,拓展學生解題思維,提高解題能力.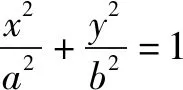


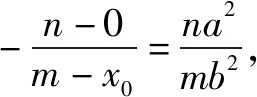
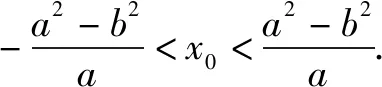
三、導數在求解函數最值過程中的廣泛應用