含風電系統中機組組合的分時段分層優化

林創

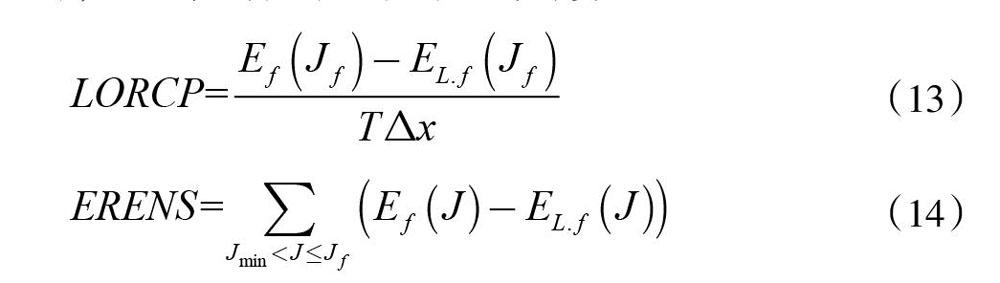
摘? 要：首先，基于隨機生產模擬算法（probabilistic production simulation algorithm，PPSA），建立了包含風電、火電、水電、氣電和抽水蓄能等類型的機組組合優化模型，其特點是可通過PPSA提供的可靠性指標和靈活性指標形成約束，從而保證機組組合方案的優化必然滿足可靠性和靈活性的要求;然后，以PSO、PL和動態規劃三種算法構成分時段與分層的優化策略，對機組組合方案的經濟性進行優化;最后，利用所提出的模型及策略對10機和32機系統的機組組合問題進行求解，驗證了該方法的準確性和有效性。

關鍵詞：隨機生產模擬算法;機組組合;分時段優化;分層優化

中圖分類號：TM614 文獻標志碼：A? ? ? 文章編號：2095-2945（2019）10-0011-04

Abstract： Firstly， based on the probabilistic production simulation algorithm （PPSA）， an optimization model of unit commitment is established， which includes wind power， thermal power， hydropower， gas power and pumped storage. Its characteristic is that the reliability index and flexibility index provided by PPSA can be used to form constraints， so as to ensure that the optimization of unit commitment scheme must meet the requirements of reliability and flexibility. Three algorithms， PSO， PL and dynamic programming， are used to form a time-division and hierarchical optimization strategy to optimize the economy of the unit commitment scheme. Finally， the proposed model and strategy are used to solve the unit commitment problem of 10-machine and 32-machine systems and the accuracy and effectiveness of the method are verified.

Keywords： probabilistic production simulation algorithm; unit commitment; time-interval optimization; layered optimization

引言

機組組合是實現電力系統安全運行和經濟調度的基礎環節，其主要目的是制定單目標最優或多目標整體較優的調度計劃。近年來，隨著風電等間歇性能源的大規模并網，機組組合問題中的不確定性顯著增加，為電力系統的調度工作帶來嚴峻挑戰，一方面傳統的機組組合問題求解模型無法有效地考慮風電的隨機性與波動性，導致所得方案的適用性大打折扣，另一方面對于完備的求解模型，卻缺乏精確且高效的優化算法，不利于實際的應用。

針對以上兩個難點，國內外的專家學者們在此領域中開展了大量的研究。現有的機組組合模型主要依據風電的功率點預測[1][2]和場景生成[3][4]兩種方法建立，但存在無法確定最優備用及運行點等難題。文獻[5]關注了機組組合求解結果在任一瞬間之間的牽制問題，并建立了新的數學模型。文獻[6]基于風電預測的SSCUC模型，將風電的不確定性模型分解為1個確定場景和2個極限場景，簡化了求解復雜度。關于求解方法，混合整數非線性規劃、動態規劃[7]以及智能優化等算法[8]均在當前研究中有所應用，但單獨的一種算法都具有局限性。

受上述思路及研究的啟發，本文仍主要從機組組合模型的建立和優化算法的選擇兩方面開展研究。首先，鑒于已有的機組組合模型在生產中適用性較差，所以本文另辟蹊徑，基于隨機生產模擬算法（PPSA）的思想建立了機組組合的模型。歷經長足的發展，目前的PPSA研究已能夠考慮諸如負荷波動、機組停運、新能源出力波動等因素，基本具備分析評估系統運行計劃的功能[9][10]。對于機組組合的優化方法，本文選擇了動態規劃、優先順序（priority list，PL）和粒子群算法（particle swarm op-timization，PSO）三者相結合的方法進行求解。

1 機組模型

1.1 風電機組

本文采用如下的七參數混合Weibull分布描述風速[11]，相比于兩參數形式，多參數的混合Weibull分布對段周期內的風速擬合精度更高。

風電機組的出力函數與風速密切相關，且具有切入與切出風速的特點，式（4）所描述的風電出力特性較為經典可靠，且滿足精度要求。

式中，Pw0為額定輸出功率，vr為額定風速，vco為切出風速，vci為切入風速。

1.2 火電機組

火電機組正常運行時，需保證發電功率不低于規定的最小穩定出力，剩余容量因具有一定的調節能力可作為調峰或旋轉備用，但機組受最大爬坡率約束，同時運行經濟性下降。因此，火電機組的模型包含最小穩定出力和可調節出力兩部分，后者還分為調峰容量和備用容量，并考慮爬坡約束及額外成本，如式（5）所示。

式中，Pt.u、Pt.f、Pt.a和Pt.s分別為單機容量、最小穩定出力、調峰出力和備用容量，Rt.f、Rt.s分別為最小穩定出力率和備用率，Tt.f和Tt.r分別為平均故障間隔時間和故障恢復時間，Rt.cv為最大爬坡率，Pg、Et.a和Et.c為模擬周期T內的平均出力和調峰、爬坡電量，△t為爬坡時間，Kt.c為爬坡懲罰系數，Ct.a為調峰發電的單位成本。

1.3 燃氣輪機

與常規燃煤機組相比，燃氣輪機的啟停性能更好，且爬坡能力更強，但發電成本高，所以為兼顧經濟性而僅作調峰電源使用。燃氣輪機本質上是火電，出力模型與火電類似，但需要增加最大發電小時數Tmax體現“兩班制”運行模式，如式（6）所示。

式中， Pp.u、Pp.f、Pp.a和Pp.s分別為調峰機組的單機容量、最小穩定出力、調峰出力和備用容量，Rp.f、Rp.s分別為最小穩定出力率和備用率，Ti為機組在各時段的發電時間。

1.4 抽水蓄能機組

運行于抽水工況下的抽蓄機組相當于電動機負荷，將從電網吸收的有功轉化為水能進行儲存，最大儲存量由最大蓄水庫容決定，而每小時的抽水量根據系統需求確定，模型如式（7）所示。

式中，Em.ps、Eps分別為抽水機組消耗的發電量和最大抽水庫容所儲存的水能，Pm.ps為抽水消耗的功率，Tps為抽水持續時間，？濁m為轉化效率。

1.5 停機備用機組

處于停機備用狀態的機組，主要考慮其啟動費用對運行經濟性的負面影響[12]，以及最小停運時間和最小運行時間兩項約束[13]，模型如式（8）所示。

2 隨機生產模擬算法

2.1 基本原理

在諸多的生產模擬算法之中，綜合運算效率和精確度兩方面，等效電量函數法（Equivalent energy function method， EEF）的表現更為優異[14]，這是一種嚴格的算法，且計算速度快，本文的PPSA是基于EEF法進行設計。

等效電量函數根據式（9）定義。假設安排了i-1臺機組后，已知E（i-1）（J），且第i臺機組容量和隨機停運率分別為Pi和qi，則E（i）（J）據式（10）計算[15]。

當系統含有n臺機組，根據E（n）（J）可計算EENS（電力不足期望值，Expected Energy not Sup-plied）和LOLP （電力不足概率，Loss of Load Proba-bility），如式（11）和（12）所示。通過約束LOLP或EENS，可使機組組合方案滿足系統的可靠性要求。

2.2 靈活性指標

在PPSA中，本文還基于EEF的思想引入兩項用于評估系統靈活性的指標，分別為LORCP（調峰容量不足概率，Loss of Regulating Capacity Proba-bility）與ERENS（調峰電量不足期望值，Expected Regulating Energy Not Supplied），可根據式（13）和（14）進行計算。

3 優化策略

3.1 分時段優化

由于風電出力具有隨機性和波動性的特點，同時大多數地區的負荷也表現為顯著的峰谷特性，所以大規模的風電接入后，電力系統在每個時段的最優機組組合方案都會隨著風電出力與負荷的波動而有所變化，并且由于火電開機費用高昂、停機機組受最小啟停時間約束以及備用容量受最大爬坡速率影響等問題，各個時段之間的機組發電計劃呈現更加復雜的牽制關系。因此，最優的機組發電方案隨時間推移發生變化，所以分時段優化的過程借鑒了動態規劃思想，考慮前后兩個時段狀態轉移所產生的影響。另一方面，對于每個時段內的最優機組發電方案，本文綜合利用了PL和PSO兩種方法，其中PL為PSO指定了搜索方向，使PSO提高結果的最優性，并加快收斂速度。

3.2 分層優化

分層優化是針對調峰機組、抽水蓄能機組等調峰電源采取的策略，由于此類電源往往需要綜合各個時段的可靠性和靈活性情況來安排發電計劃，所以先對其余機組的組合方案進行第一層優化，再根據第一層優化后各項約束及目標的情況，對調峰電源是否安排開機，以及投入發電的機組數量和具體時段等問題進行第二層優化。另一方面，由于調峰電源的機組數量較多、單機容量較小，所以采取分層優化策略后，可以有效減小求解規模，同時這也有利于發揮調峰電源“削峰填谷”的運行特性。

3.3 優化流程

綜合以上兩種優化策略，得到完整的優化流程如圖1所示，優化目標是在滿足系統可靠性、靈活性約束以及各項機組運行約束的前提下，實現系統運行的經濟性最優和最小化火電開機。

4 算例

算例部分的內容主要分為以下兩個方面：首先，以文獻[16]中10機系統的機組組合問題驗證本文所用優化模型的準確性;然后借助IEEE RTS-86的32機系統說明本文完整優化流程在加入風電后的有效性和合理性。

4.1 模型校驗

對文獻[16]中10機系統的機組組合問題進行求解，所得結果與文獻[16]的最優方案相同，并將該方案代入本文模型進行模擬，通過對比煤耗的計算結果驗證優化模型的準確性，文獻[16]與本文的結果分別為81245.5和81201.9噸標煤。由于本文的模型采用了線性化的機組煤耗曲線，所以計算結果呈現一定的差異，但差別僅為0.05%，可見本文基于PPSA所建立的機組組合模型具有較高的準確度。

4.2 含風電的機組組合優化

由于10機系統僅包含火電機組，無法體現本文組合優化模型對于含風電的復雜電力系統的適用性，所以采用IEEE RTS-86的32機系統測試本文完整的優化模型，系統和機組基本信息見文獻[17]，并接入250臺單機容量為4MW的風電，Weibull分布參數見文獻[18]，缺電成本2000元/MWh，棄電成本1000元/MWh。

接入風電后，系統各時段的機組組合如表1所示，總運行成本為1150.9萬元，若采用傳統的PL法進行優化，總成本則為1274.5萬元，可見本文方法具有更好的經濟性。另一方面，與接入風電前最優機組組合方案的總成本1076.78萬元相比，風電使系統的經濟性下降，原因是風電的發電成本較高且火電啟停頻繁。為應對風電出力的隨機性，燃氣與抽水蓄能機組的開機數量和運行時段增加，目的是保證系統滿足可靠性與靈活性約束。

5 結論

本文基于隨機生產模擬的思想，結合PSO、PL和動態規劃三種優化算法，提出了針對含風電電力系統的機組組合優化方法。經兩個算例驗證，可見本文所提優化模型的計算精確度較高，同時可以對含風電系統的機組組合方案進行有效的優化，優化結果反映出風電對發電安排的影響，亦即該方案可滿足系統消納風電電量的要求。與其它算法相比較，本文所建立的模型由于考慮了機組的隨機停運、特殊機組的運行特性以及風電的出力波動性等因素而具有更高的合理性和實用性，為求解機組組合問題提供了新的思路。相比傳統優化算法，本文的優化方法在求解速度上表現較差，后續工作可以進一步提升其計算性能。

參考文獻：

[1]Chen C L. Optimal Wind-Thermal Generating Unit Commitment[J]. IEEE Transactions on Energy Conversion， 2008，23（1）：273-280.

[2]周瑋，彭昱，孫輝，等.含風電場的電力系統動態經濟調度[J].中國電機工程學報，2009，29（25）：13-18.

[3]王勇超，陳皓勇，禤培正，等.基于最優場景集的含多類型電源魯棒調度[J].電網技術，2016，40（2）：354-362.

[4]謝敏，閆圓圓，劉明波，等.含隨機風電的大規模多目標機組組合問題的向量序優化方法[J].電網技術，2015（1）.

[5]韓學山，李本新，李榮，等.應對風電間歇性的火電機組組合模型構建與分析方法[J].電網技術，2017（5）.

[6]汪超群，韋化，吳思緣.計及風電不確定性的隨機安全約束機組組合[J].電網技術，2017（05）：66-74.

[7]Rouhi F. Unit Commitment in Power System by Combination of Dynamic Programming， Genetic Algorithm and Particle Swarm Op-timization[J]. Indian Journal of Science & Technology， 2014.

[8]Sun L， Zhang Y， Jiang C. A matrix real-coded genetic algorithm to the unit commitment problem[J]. Electric Power Systems Research， 2006，76（9-10）：716-728.

[9]王錫凡.電力系統優化規劃[M].水利電力出版社，1990.

[10]陳亞博，盛戈皞，黎建，等.含光伏和風電的電力系統隨機生產模擬[J].電力系統及其自動化學報，2015，27（5）.

[11]王松巖，于繼來.短時風速概率分布的混合威布爾逼近方法[J].電力系統自動化，2010，34（6）：89-93.

[12]韓學山，柳焯.考慮發電機組輸出功率速度限制的最優機組組合[J].電網技術，1994（6）：11-16.

[13]楊冬鋒，周蘇荃，鮑鋒.風電并網系統低谷時段的調峰能力分析[J].電網技術，2014，38（6）：1446-1451.

[14]李林川，王錫凡，王秀麗.基于等效電量函數法的互聯電力系統隨機生產模擬[J].中國電機工程學報，1996（3）：180-184.

[15]王錫凡，王秀麗.隨機生產模擬及其應用[J].電力系統自動化，2003，27（8）：10-15.

[16]李整，譚文，秦金磊.一種用于機組組合問題的改進雙重粒子群算法[J].中國電機工程學報，2012，32（25）：189-195.

[17]Allan R N， Billinton R， Abdel-Gawad N M K. The IEEE Reliability Test System - Extensions to and Evaluation of the Generating Sys-tem[J]. Power Systems IEEE Transactions on， 1986，1（4）：1-7.

[18]Karaki SH， Chedid RB， Ramadan R. Probabilistic performance assessment of autonomous solar-wind energy conversion sys-tems. IEEE Trans on Energy Conversion， 1999，14（3）：766-772.