找準基本教研點 做我們能做的事
姚志富
(安徽省蕪湖市第十二中學 241003)
一、中學課堂教學是基本教研點的一片沃土,我們要深耕細作
對來自課堂教學這些教研點的研究,不僅可以豐富我們的教學內容、方法、技巧、思想從而極大地開闊我們的教學視野,還有可能幫助我們從教學人變成教育人.
1.課例的分析和點評
(1)好課的評價標準
①要看教學目標實現度,即必須實現這節課的教學目標,這要從目標的確定和教學各環節的實施效果兩方面評價.
②要看教材的處理,即在教學過程中是否能夠準確理解教材,駕馭教材,創造性地使用教材.我們主要從知識傳授是否準確、把握重難度、突出重點、突破難點的過程和方法是否合理,以及對教材內容的調整是否科學,是否合理選擇了教學方法.
③要看教學環節的設計與實施.主要看教學思路的設計是否符合教學內容的要求,是否符合學生實際情況,還要看教學思路是否層次分明、脈絡清析,看各環節銜接是否嚴謹、自然并符合邏輯規律和學生認知規律.
④要看教學方法與手段.主要看方法和手段是否符合教學目標、教學內容的要求,看是否符合學生的身心發展要求和認知特點,看是否充分利用現有的教學手段來輔助教學.
⑤看教師基本功.主要看板書、教態、語言,即教師出手相是否好,語言功底對數學教師很重要,簡煉重要,精煉及重要.
(2)有效的教學方法
①要根據教學內容而定.起始課、概念課就不太適合啟發式的教學方法和合作、討論式的教學方法,講授法更適宜,而復習課就不太適宜講授法,對內容熟悉的又有一定的方法基礎,課堂教學要讓學生動起來,在動的過程中發現問題、解決問題、總結提煉問題.
②要根據學生自身的特點.主要是指學生認知水平和思維水平,合作也好,議論也罷,不能走形式,要讓學生能走進活動中去,否則就是一場戲.
③要根據教師自身的特點.每個教師都有自己喜歡的教學方法,古板嚴謹的教師有的是,尤其是數學教師,這也未必就是壞事,有些教學法我們很多人是玩不動、玩不轉的,但是偶爾為之是必要的,否則學生是不喜歡你的,也會喪失興趣的.
2.教材解讀
這是我們更進一步理解、掌握并駕馭教材的有效途徑,也是很基礎的教研點.教材解讀有很多種方式,但必須把握的應當有以下幾方面:
(1)明確教學內容的課程目標和學習目標,以及這些內容對前后知識的貫穿作用,教學主線是什么,選擇什么樣的教學方法來實現課程目標和學習目標.
(2)教材內容的具體研讀
包括章頭圖和引言的解讀,對具體的概念、定義、公式、定理、推論以及例習題,練習題如何處理得要認真推敲打磨,這些方面主要是依據教材和教學大綱,結合個人的理解,但是我們能明顯地感受到不同的教師會有不同的眼界和思維層次.
(3)對教學的建議
教材內容是“死”的,但是如何消化教材,如何運用教材,不同的教師會有不同的想法和做法,教學建議就顯得很重要,這不僅體現出自己的認識水平,更是給別人的中懇建議和素材.這是教材解讀有特色顯個性的地方,建議可以從本章、本節內容的知識結構,重難點的合理定位,開拓創新地突破難點,鼓勵學生探究性學習等幾方面考慮.
3.解題方法及其解題教學的研究
包括具體數學問題的多途徑解決及思考,解題思想和方法的研究以及高考復習過程中復習方法及相關問題的研究,數學競賽問題的研究,這類問題歸結起來就是提出問題,分析問題和解決問題,在嘗試一題多題、命題意圖分析、問題源分析的基礎上,上升為思想方法的分析和指導,直至達到以一個問題解決一類問題的目的.這一基本教研點入口較寬,可以從一個小問題開始,嘗試一題多解,一題多變再上升到一類問題解決方法的概括和總結.
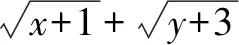
解法一(函數法)x+y=5,∴0 解法三(三角函數法)令x=5sin2θ,y=5cos2θ. 這應當是奧賽教練員和愛好競賽題研究的數學教師可以做的事,像安振平教授對不等式的研究不僅成果頗豐而且成果顯著,像安師大郭要紅教授對不等式和初等平面幾何的研究也是成績斐然,在這方面青年教師可以大膽嘗試,相信會有大回報 這是一個永恒的話題,因為不會解題的老師絕對不是一個好老師,只會解題而不會一題多解、一題多變、融會貫通的老師同樣不是一位好老師,在這個領域我們可以大有作為,可以從兩方面入手: (1)是解題思維起點的合理性研究,即你是怎么想到的,為什么這么想,這對提高學生合理應用知識和方法有幫助. (2)是對解題過程中思維受阻從思維的合理性進行分析,努力找出原因并力爭沿著原來的思維路線在優化思維方法的前提下解決問題. (《在數學案例分析過程中逐步成長》——《數學通訊》2014.4) (1)數學文化沒有作為數學教育不可或缺的重要組成部分,給大家的感覺是數學沒有歷史,沒有歷史傳承與階段發展史,呈現給大家的僅僅是數學成果,這既與教科書編排沒有很好地融入歷史觀、價值觀有關,也與教育者急功近利的思想有關. (2)課堂數學中對數學文化價值的教育活動內容很單薄,零碎而不成體系,有些內容在章頭圖中,有的內容在“探究與發現”、“閱讀與思考”等閱讀材料中,讓師生感覺可有可無,存在感不突出. (3)當前的高考中將數學文化列入考試內容之一,進一步弱化了數學文化價值的教育活動,如2015年全國課標1卷文科數學第(6)題,以文言文與白話文兩種形式呈現,那文言文以及古代的這個數學問題存在又有什么必要呢?不是徒有其表嗎?以這樣的形式呈現又能說明數學文化什么樣的價值呢?數學文化教育的意義又在哪里? (1)樹立正確的數學史觀.數學史的內容是非常豐富的,數學史是歷史,它有過程,有思想方法,有正確的理論,也有疑問和謬誤.我們在日常教學中可以挖掘數學相關理論及思想方法推演及演化過程、發展規律,對某些領域代表性的數學家可以研究其思維方式和方法.這對我們來說是一個啟示,對某些問題的研究可以少走彎路,很方便地尋找到正確的解決問題的方法.因此在日常教學中,我們對某些問題研究時可以剖析數學家研究的曲折經歷,思維方式和研究方法,讓學生在這一過程既有情感共鳴,也有與數學家共同研究的實踐經歷. 例如人教A版選修1-1中“為什么截口是橢圓”這個問題 . (2)讓學生感受到數學史就是一部創造史.學習數學史,是讓我們感受到數學家“再創造”的思維過程,體會到數學史與其他歷史一樣,是一部社會發展的創造史,是以推動社會發展為根本目的.如引進負數是社會發展的需要,引進復數是為解決有關數學問題服務的,是為健全數系服務的.因此我們理解有關數學概念,要有“形”還要跳出“形”,最后融合社會需要這個根本,即數學是人類文化的重要組成部分,在推動社會進步和發展的過程中起著重要的作用.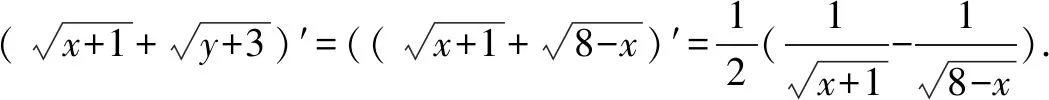
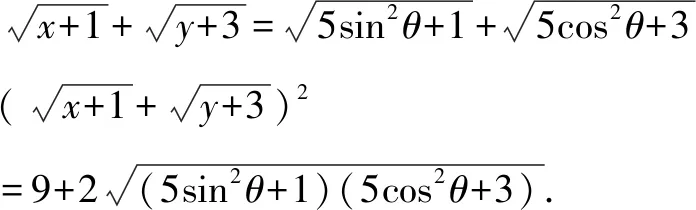
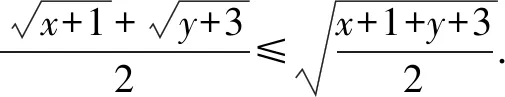
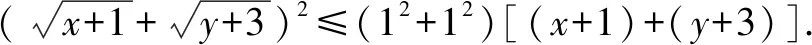
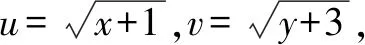
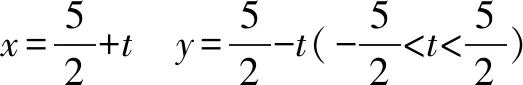
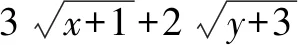
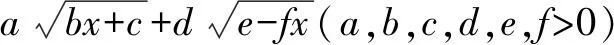
4.關于高中數學競賽題的研究
5.關于中學解題教學的研究
二、開展對課標的研究,讓我們站得更高,看得更遠
1.當今關于數學文化價值的教育現狀
2.如何有效開展數學文化價值的教育

