高中數學概念教學之我見

楊武健 張啟蒙

(浙江省天臺中學 317200)

一、當前概念教學的現狀

在當前的數學課堂教學中，仍然存在輕“概念學習”，重“例題講解、練習模仿、習題鞏固”的現象.為獲得學生眼前的數學成績，高中數學概念教學只剩下干巴巴的“一個定義，兩項注意，幾個反例……”.因此，造成概念的產生是空降的，概念的過程是空泛的，概念的體驗是膚淺的，概念的規定是莫名的.數學課堂的“習題教學”與“概念教學”是割裂的、互斥的，甚至是風馬牛不相及的.由于數學概念在學生的腦海中只殘留下模糊的片段，導致學生在解決數學問題時只能是簡單的模仿，機械的重復，熟能生巧而已.

數學從根本上來說是玩概念的.數學概念是數學學科的基石，也是培養學生數學素養的最好載體.在數學課堂教學中，為什么要提出一個概念？如何恰當地定義一個概念？如何體現一個概念定義的合理性，如何讓學生體驗概念形成的過程，體會概念定義之科學性和嚴謹性？如何及時鞏固概念教學之成果，是值得每一個數學教育者深思的.

二、高中數學概念教學的幾點改進

1.講清數學概念的源和流

概念的“源”即指概念的“前世今生”，概念的“流”即指概念的“實際應用”、“未來走向”.一個學生剛開始接觸一個概念，只有清楚它的來龍去脈，才能深深地留下“初識”.這一“初體驗”能很好地激發學生的學習興趣，誘惑學生的“探索欲望”，培養學生的應用意識.對于數學概念，學生只有“知其然，知其所以然”，才能避免機械地記憶，生搬硬套地使用.請看案例1《數系的擴充與復數的概念》.

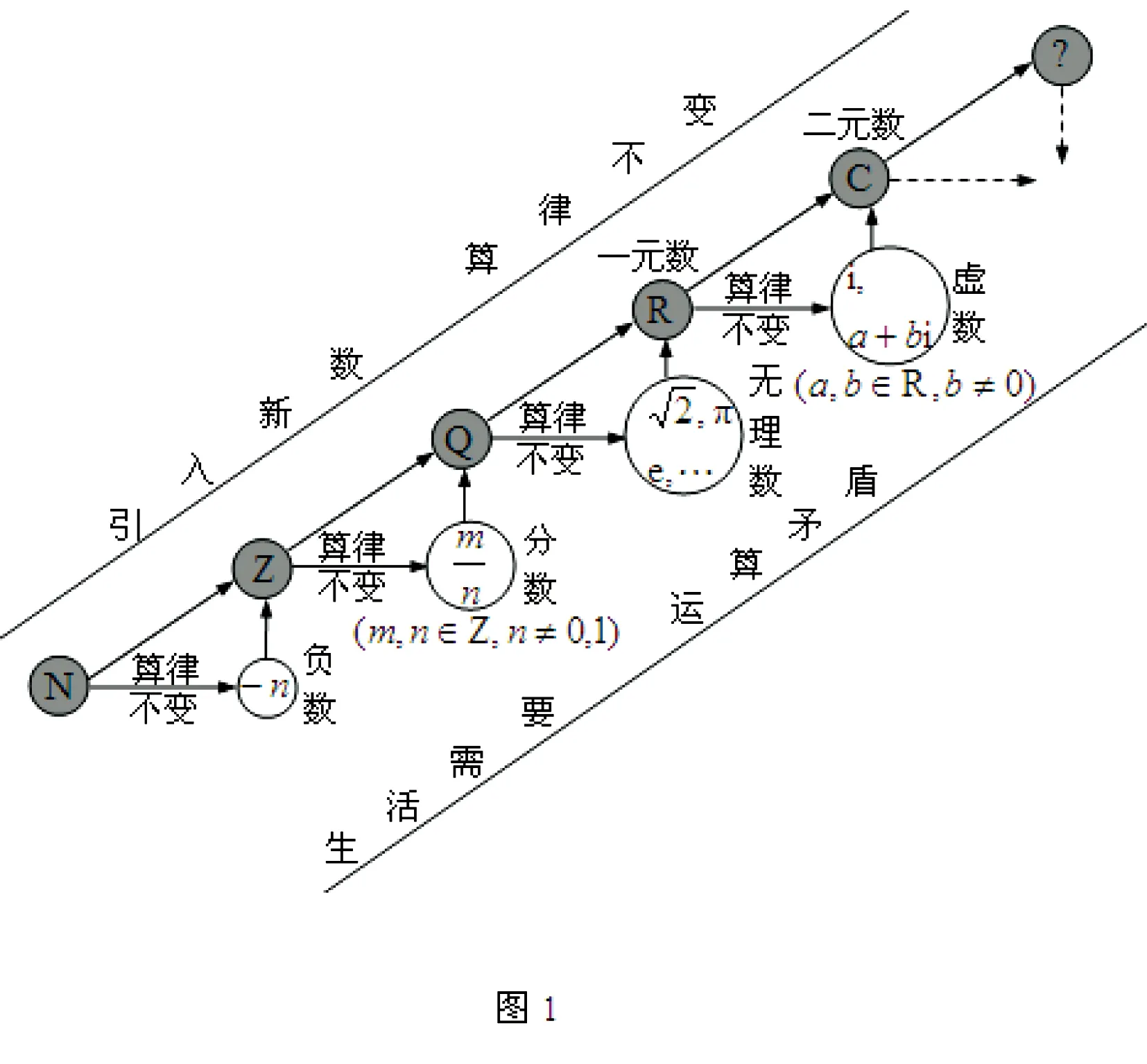
案例1 數系的擴充與復數的概念

首先，我們要講清數系發展的緣由，數系發展的規律.這樣才能使學生明了復數產生的背景，理解復數發展的緣由，感受數系發展的規律，深刻體會復數產生的必然性，發展的合理性.也為今后數系的進一步擴充打下基礎.

因此，在《數系的擴充與復數的概念》這堂課中，一定要講清從自然數發展到實數的產生緣由：一是由于實際生活的需要；二是數學內在發展的要求.如從自然數擴充到整數，最初源于古代物物交換的需要，以及物物交換所產生的多少問題，原有的自然數就不夠用了，它無法解決負數問題，于是引入負整數成為一種必然.這樣既繼承了原有的加法法則即原有的算律不變，又發展了新的算律——“減法”產生了，既解決了實際問題，又解決了形如方程“x+3=2”在自然數范圍內的無解情況，使得數學得到了進一步的發展.這樣復數的產生就不難理解了.它要解決負數開方問題.讓原有的一些在實數范圍內無法解決的問題得以解決.

一個概念，只有了解概念之“源”，才能思考概念之“流”，從而學會數學之思.概念之“流”，是數學發展之“未來”，也是數學未來之趨勢.了解數學之“流”，有利于提升對數學的再認識.請看案例2《復數域還能擴大嗎？》.

案例2復數域還能擴大嗎？

我們經歷了數集從自然數集到復數集的擴張，在每一次擴張中，人們都遵循了如下的幾條原則：(1)擴張的目的；(2)擴張后的集合要擴大；(3)保持原有的運算；(4)擴張的最小性與唯一性.我們已經看到，數集的每一次擴張，人們都能夠解決一些在原數集中不能解決的問題，所以人們自然會想到，能否將復數集再進行擴充，使得在擴充后的新數集中能夠進行四則運算，并且復數集是新數集的一個特例.不僅如此，還希望這新的數集可以同空間向量等同起來(類比實數是一元數，復數是二元數，自然猜想新數集是三元數)，使兩者的加法運算相一致.

假設K是這樣一個新數集.于是在取定了直角坐標系的空間中表示向量的三元數組(a,b,c)其中a,b,c∈R應該同K中的元素q=a+bi+cj對應起來，其中i是虛數單位，即i2=-1，j是添加到復數集中的一個新數.為了與復數集一致，在K中自然規定：a1+b1i+c1j=a2+b2i+c2j，當且僅當a1=a2，b1=b2，c1=c2.于是當a+bi+cj=0時，必有a=b=c=0.由于向量加法的定義是(a1,b1,c1)+(a2,b2,c2)=(a1+a2,b1+b2,c1+c2)，所以在K中的兩個元素的加法自然規定為(a1+b1i+c1j)+(a2+b2i+c2j)=(a1+a2)+(b1+b2)i+(c1+c2)j.i與j相乘的結果自然要求屬于K.故設i×j=a+bi+cj ①.用i左乘①式的兩端，且由i2=-1，有-j=ai-b+ci×j， 也就是ci×j=b-ai-j. ②用c乘①式兩端后減去②式的兩端得(ac-b)+(bc+a)i+(c2+1)j=0.

由此得c2+1=0，這與c是實數矛盾.這表明新數集K是不可能存在的,所以復數集是滿足加減乘除的最大集合.

清晰概念之“源”是對概念之“流”的進一步深化認識，也是數學認識與思考的再經歷，他是數學的深度學習，也是數學思維之源，方法之根.

當然，教師要想把握好每個概念的“源”與“流”，必須練好內功，苦讀數學史，清楚數學發展的整個歷程.只有不斷積累，才能厚積薄發，得心應手.

2.道明數學概念給出的“情” 與“ 理”

數學概念給出的“情”即指“合情”，指的是每一次說明能符合我們的直觀感知,也能經得起邏輯推理；數學概念的“理”即指數學概念的給出都能經得起嚴格推理，具有科學性和嚴謹性.同時數學概念的給出還要體現數學所要追求的“簡潔”、“優美”，體現數學概念的美，散發數學的無窮魅力.只有這樣，才能用數學的“冰冷”催生學生的“火熱”.

(1)數學的概念要符合人的直觀感知，也為數學的進一步研究提供最優的奠基

如：為什么要規定平行于x軸或與x軸平行的直線的傾斜角為0°呢？一為概念的完備性與嚴謹性，因為直線傾斜角剛開始定義了直線與x軸相交時，未包括這一類，若不加以補充，數學研究對象不完備；二為對象的唯一性，若定義為0°或180°，那就不能建立傾斜角與直線的一一對應關系，也構建不了函數關系.另一角度，也可從規定的延續性與合理性角度理解.因為直線與x軸相交時，規定x軸正方向與直線向上方向的夾角，而一般向上方向指的是正方向，而0°也比180°更符合人的視覺感受.再如：為什么把直線的斜率定位為傾斜角的正切值，而不是正弦值或余斜值？若定義為正弦值，一則會出現兩條直線對應同一斜率，如45°與135°，而正弦的有界性也與傾斜角給人的視覺感受不符，如傾斜角為90°直線是非常“陡”的，正余弦都無法體現這一點.那么用正切值去定義即符合人的直觀感知，又能從數值上體現傾斜角的變化規律.

(2)數學的概念是講“理”的

如：為什么將復數的形式寫成z=a+bi(a,b∈R)，若教師不解釋，學生將會疑惑不解.為此，我們可以為學生設計這樣的問題. 根據數系擴充的規律，數系擴充后，原有的運算律在新的數系中仍然適用，那么將復數i與實數進行四則運算，它能產生哪些結果？它們能否用一種形式加以概括？這樣設計，可以讓學生明了復數定義的“理”.

再如：一般地，兩個復數為什么不能比較大小呢？若復數可以比較大小，如i與1，若i>1，則i2>12，得-1>1顯然不成立；同樣可以證明i<1，i=1都是不正確的.否則，復數系就不能繼承原有實數系范圍內的運算律.這樣又從另一方面說明數學是講“理”的.

(3)數學的概念是嚴謹的

如：規定a0=1(a≠0)，目的為了使得指數冪運算性質am·an=am+n(a>0,m,n∈R)成立，否則當m+n=0時，上述運算性質不成立.同樣規定 0！=1，也是如此.

(4)數學的概念是求美的

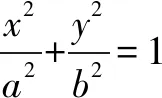
(5)數學的概念追尋一種尋“定”求“最”的原則

如在直線與平面的所成角定義中，規定平面內的一條斜線和它在平面上的射影所成的銳角為直線與平面所成的角.這既符合人的直觀想象，也符合數學的邏輯推理、數學定義的一貫原則.因為最小角定理保證了斜線與它在平面內射影所成的銳角為斜線與平面內任何一條直線所成的角中最小的且唯一.異面直線所成角，二面角等概念亦是如此.

3.創好情境，舉對例子，設好問題

數學的一個本質是抽象，它的一個突出表現即為概念.學生對于概念的把握總有許多困難，這就要求我們設好問題串，引導學生思維，逐步化解難點，直擊數學本質.

4.準確定位“例題教學”與“ 概念教學” 之間的關系

在當前功利心的驅使下，很多概念教學常常“變異”成“15分鐘的概念講解”+“25分鐘的例題講解及練習鞏固”，這樣的授課把概念的講解服務于例題教學，看似得到了很大的眼前利益，實則犧牲了學生的長遠發展.因為每一個概念的產生、發展、應用以及背后的“過程”蘊含了豐富的數學思想方法、深刻的數學精神.明確例題教學也是概念教學的有機組成部分，并在例題教學中讓學生進一步理解數學概念本質.

高中數學概念的教學，是高中數學教學的重中之重，是培養學生素養的主陣地，它要求我們學會用數學的眼光看問題，用數學的語言表達問題，會用數學的思維解決問題.