基于聲干涉特征匹配的水中目標運動分析研究

徐國軍， 張林， 韓梅， 范培勤

(1.海軍潛艇學院 二系， 山東 青島 266199； 2.青島海洋科學與技術試點國家實驗室， 山東 青島 266237)

0 引言

水中運動目標被動定位一直是水聲工作者的重點研究內容。以簡正波理論表達海洋波導特別是淺海波導聲場時，不同號簡正波相互干涉，使低頻聲場具有穩定的干涉結構，將這種干涉特性引入水中運動目標的被動定位，已成為近20年來水聲學的熱點研究方向。

淺海聲強譜在距離- 頻率平面上會呈現明暗相間的干涉條紋。條紋斜率、目標距離及頻率的關系可用波導不變量β來表征[1]。β最早由俄羅斯學者Chuprov提出，之后關于β的計算方法[2-4]及其在聲學定位方向的應用研究不斷發展[5-12]。如文獻[5]利用雙水平線列陣獲取的目標輻射噪聲譜干涉結構，建立了一種水中目標距離估計方法；文獻[6]利用垂直線列陣，通過聲場干涉條紋構造了一種基于虛擬引導聲源的水中目標定位方法。文獻[9]基于波導不變理論，建立了一種基于擴展卡爾曼濾波的動目標距離連續估計方法。上述算法主要基于固定位置的線列陣或單水聽器獲取的目標噪聲時間- 頻率(對應于距離- 頻率)譜圖，通過譜圖條紋結構構建相關算法實現目標距離估計。但在實際工程應用中，特別是對于水下機動觀測平臺，利用聲場干涉結構實現水中目標的運動分析研究還未見報道，更多的見于純方位目標運動分析(TMA)及其改進方法[13-15]，該類算法普遍存在解算時間較長、平臺機動要求高等特點。

文獻[16-17]基于運動目標的距離時變特性，提出了距離特征量，構建了基于時間- 頻率譜圖干涉條紋的距離特征量提取方法，通過距離特征量實時反映目標距離的變化情況。文獻[17-19]針對艦船目標輻射噪聲時間- 頻率譜圖建立了適用于低信噪比、不連續條紋下的目標距離特征量提取方法；文獻[20]利用方位信息、通過構造距離特征量和目標方位的關系模型，給出了一種估計淺海距離特征量的補充方法，理論上分析了水中運動目標方位信息與距離特征量之間的聯系。上述有關距離特征量的理論分析建立了目標距離的變化與聲場干涉條紋之間的聯系，為距離特征量的進一步應用提供了理論支撐。

為改善機動觀測平臺的水中目標運動分析問題，本文在前述距離特征量研究基礎上，聯合兩方位- 兩距離目標運動分析，基于循環匹配尋優處理，建立一種距離特征量匹配分析的目標運動要素估計方法。首先從理論上分析淺海聲場干涉條紋現象的成因，介紹干涉條紋信息建立距離特征量估計方法；然后建立以目標初距、瞬距為循環因子，融合兩方位- 兩距離目標運動參數的計算方法，獲取關于距離特征量的匹配代價因子，將每次循環過程中計算的代價因子，分別在對應目標距離、目標航向和目標速度估計結果圖中可視化顯示，從而實現目標運動要素估計；進一步，對基于距離特征量信息的目標運動分析展開可觀測性分析。最后利用仿真和海試數據對算法進行驗證。

1 波導不變性及距離特征量

1.1 淺海聲場波導不變性

根據淺海聲場簡正波表達式，頻譜為A(ω)、深度為zs的點源發出角頻率為ω的聲信號，當接收器深度為zr、距聲源水平距離為r時，用簡正波表示的聲壓為

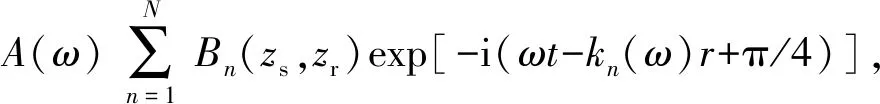
(1)

式中：n為簡正波序號，由于截止頻率的存在，N與ω的取值有關，ω=2πf，f為聲信號頻率；Bn(zs,zr)=(2π/[kn(ω)r])1/2Ψn(zs)Ψn(zr)，kn(ω)為水平波數，Ψn(z)為第n號簡正波的垂向分布函數；t為聲信號傳播時間；i為虛數單位。

結合(1)式，有聲強為

(2)

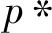
(2)式等號右端相加的兩項中，第1項是非相干項、第2項是相干項，相干項由兩號簡正波兩兩干涉相互疊加而成，如果每兩號簡正波干涉形成的條紋斜率互不相同，則多號簡正波形成的干涉平面必然雜亂無章。然而通常在淺海波導傳播的聲場中，任意兩號簡正波形成的干涉條紋往往具有相同的斜率，如圖1中的干涉條紋。Chuprov[1]根據條紋的斜率定義了波導不變量β：

(3)

對于距離- 頻率譜圖平面上的干涉條紋，可認為其聲強處處相等，滿足條紋上不同點的聲強變化dI=0，即：

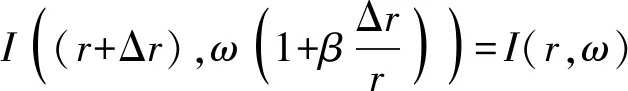
因此可知距離- 頻率譜圖中(r，ω)處的聲強與(r+Δr，ω+ωβΔr/r)處的聲強大小一致，其中Δr為距離變化量；或者距離- 頻率譜圖中角頻率ω2處r距離上的聲強與角頻率ω1處r(ω1/ω2)1/β距離上的聲強大小一致。

根據文獻[12]對聲場簡正波的分類，如果聲場強度主要由海面反射- 海底反射簡正波貢獻，則聲場干涉條紋對應的波導不變量近似為1. 因此對于典型淺海環境，此時波導不變量可近似為1[8]，若某一確定條紋上的兩點為(r1,f1)、(r2,f2)，則有如下等式成立：

(4)

式中：r1、r2表示目標距離；f1、f2表示目標輻射信號頻率。

如圖1所示為聲強時間- 頻率譜圖。由圖1可見，各亮條紋近似有相同的強度譜。

1.2 距離特征量

文獻[16-20]提出了距離特征量，并依托聲場干涉結構推導了距離特征量計算方法。所謂距離特征量是指在目標聲源與接收器相對運動過程中，t0時刻目標聲源與接收器之間的距離與t時刻目標距離的比值，它描述了目標初距與瞬時距離的比值R，反映了目標距離的變化率。如果t0時刻目標距離為D0、t1時刻目標距離為D1，則t0時刻相對t1時刻的距離特征量為

(5)

利用文獻[16]提出的基于距離- 頻率譜圖的多頻段距離特征量提取方法，可實時獲取目標距離特征量，構造簡化距離- 頻率譜如圖2所示。圖2中：橫向為距離r、縱向為頻率f，圖中距離范圍為(r1,r2)，頻率范圍為(f1，f2). 以條紋AB為例，其兩端分別延長至O(0，0)點和C點，假定B(r3，f3)為該條紋上能量最強的點，F為B點在距離r1方向的投影，D為C點在距離r1方向的投影，H、G分別為A、D點在距離0方向的投影；角度φ為條紋AB與AD的夾角。

結合三角關系，利用(4)式所示距離- 頻率關系，可推導距離r1相對距離r2的距離特征量為

(6)

式中：df為時頻圖中頻率軸各采樣點的間距；MDC為時頻譜圖距離范圍即DC段對應的采樣點數；MBF為線段BF的采樣點數；f3=f1+MEF×df，MEF為時頻圖中最強點相對起始頻率在頻率軸上的點數，即線段EF對應的點數。

綜上所述可知，在實際的目標運動分析過程中，可利用實時獲取的目標輻射噪聲時間- 頻率譜圖干涉條紋，實現各時刻距離特征量的實時獲取。

2 距離特征量匹配的目標運動要素估計

2.1 兩方位- 兩距離的目標運動分析方法

以真北線為y軸建立直角坐標系，如圖3所示。在t1時刻觀測平臺位于P1點，目標位于T1點，測得方位F1、距離D1；經時間間隔t12，即在t2時刻觀測平臺位于P2點，目標位于T2點，測得方位F2、距離D2；Ht為目標航向角；兩次測量時間間隔內觀測平臺橫向位移量為x12、縱向位移量為y12，則

(7)

式中：vt為目標速度。

為了便于解算，將三角函數方程變為線性方程，為此設目標速度的橫向分量vtx=vtsinHt，目標速度的縱向分量vty=vtcosHt. 則有

(8)

(9)

由此可知，目標速度vt=[(vtx)2+(vty)2]1/2，目標航向Ht=sign(vtx)arcos(vty/vt).

在已知Ht、vt和D1的基礎上，即可按(10)式求出任意時刻的目標距離Di：

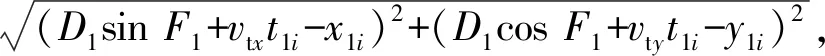
(10)

式中：t1i為第i時刻相對初始時刻的時間差。設中間變量A=D1sinF1+vtxt1i-x1i，B=D1cosF1+vtyt1i-y1i，則目標方位Fi為

(11)

距離特征量Ri為

(12)

2.2 距離特征量匹配代價因子

依據2.1節的方法計算各時刻距離特征量值，結合匹配思想構建距離特征量匹配代價因子，實現目標運動要素估計。具體構建步驟如下：

步驟1根據目標可能的距離范圍[Dmin,Dmax]，設定目標初距D0和目標瞬距Da的距離區間，確定距離區間最小步長間隔Δd.

步驟2構造初距D0j、當前時刻瞬距Dak兩層循環(j,k)，j=1，…，J；k=1，…，K，J、K分別為選取的目標初距區間和目標瞬距區間采樣數。

步驟3利用已知的初始時刻目標方位F0、當前時刻目標方位Fi、聲吶平臺運動參數(航向、航速或各時刻位置信息)，選定的目標初距D0j、計算時刻目標瞬距Dak，結合前文兩方位-兩距離目標參數計算方法，估計各時刻目標瞬距信息{ati}.

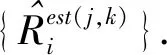
步驟5利用實測目標輻射噪聲獲取其時間-頻率譜圖，根據前文所述距離特征量計算方法，得到各時刻距離特征量{Ri,i=0,…,N}.

步驟6構造代價因子：

(13)

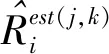
2.3 可測性分析

分析距離特征量匹配模型實現過程不難發現，該模型的本質是利用時間- 頻率譜圖呈現出的干涉條紋信息、目標方位信息、平臺與目標位置幾何關系信息，基于匹配思想實現目標運動參數估計。模型可觀測性可等效于目標方位Fi、Ri兩觀測量已知條件下目標運動分析過程的可觀測性問題。

假定目標做勻速直線運動，目標與觀測平臺的相對位置關系如圖4所示，初始時刻觀測平臺位于坐標原點。目標初始位置T0、速度vt、航向Ht，相對觀測平臺初始方位F0、初始距離D0；ti時刻目標運動到Ti(xti,yti)點，觀測平臺運動到Pi(xpi,ypi)點，目標瞬時距離Di、相對觀測平臺方位為Fi、方位變化量βi=Fi-F0.

當取目標初距D0、目標x軸方向速度vtx為狀態量時，運動方程形式如下：

(14)

ati+bηi=xpi，

(15)

則可得觀測方程組為

(16)

利用最小二乘方法，構造如下觀測方程組：

(17)

式中：N為觀測次數。顯然，模型可觀測條件為觀測矩陣G的逆矩陣存在，即矩陣G的行列式不等于0. 有矩陣G的行列式為

(18)

式中：h為觀測時刻。將變量ηi=-sinβi/Ri代入(18)式，進一步得到觀測矩陣行列式：

tith(vtxti-xpi)(vtxth-xph).

(19)

分析(19)式，可得到如下不可觀測條件：

1) 當觀測平臺靜止，即xpi=xph=…=0時，觀測矩陣行列式|G|=0，系統不可觀測；

2) 當目標與觀測平臺在同一直線運動時，βi=0，即(18)式中ηi=0，行列式|G|=0，系統不可觀測；

3) 當觀測平臺與目標均保持勻速直線運動時，系統不可觀測，此結論可證明如下：

令觀測平臺以速度vp勻速直線運動，此時x軸方向速度分量為vpx，有

xpi=ti×vpx，

(20)

此時觀測矩陣行列式為

tith(vtxti-xpi)(vtxth-xph)=

tith(vtx-vpx)(vtx-vpx)tith=0，

(21)

即觀測矩陣行列式為0，系統不可觀測。證畢。

顯然，系統可觀測(即狀態向量有解)的一個必要條件是觀測平臺必須機動，即在觀測過程中觀測平臺至少進行一次變向處理或變速處理(變速機動時目標與平臺不在同一直線)。

3 數值驗證

3.1 數值仿真

假定初始時刻運動聲源距離觀測平臺7 km、位于平臺方位0°，聲源以航向180°、速度8 m/s勻速直線運動；在解算過程中，前120 s觀測平臺速度2 m/s、航向10°，120 s開始速度變為3 m/s、逐漸轉向至280°. 基于Kraken簡正波模型，利用各時刻聲源距離仿真得到的聲強時頻譜如圖1所示。利用2.1節計算方法可在該仿真態勢條件下獲取聲源目標距離特征量(見圖5)，結合距離特征量信息，利用2.2節目標運動分析過程得到500 s時估計的聲源初距、速度和航向可視化結果圖(見圖6)，可估計目標運動要素分別為38.3 cab(7 100 m)、15.55 kn(8.0 m/s)和180.15°. 對比聲源各運動要素真值不難發現，該方法在500 s時估計的運動要素最大誤差僅1.4%，表明將距離特征量信息引入水中目標運動分析能夠取得較好的目標運動要素估計結果。

目標輻射噪聲在海洋中傳播時，由于受到海洋環境影響，接收信號信噪比會存在不同程度的降低，即其時間- 頻率譜圖干涉條紋將出現模糊或斷續的現象，由此獲取的距離特征量會相應存在誤差，文獻[18-19]對此進行了詳細介紹，并提出了提高距離特征量精度的提取方法。為分析距離特征量對算法估計的影響，表1給出了距離特征量取不同的隨機誤差、在不同時長條件下估計的目標運動要素估計結果，包含估計的具體數值及對應的估計誤差，具體可視化結果如圖7～圖15所示。

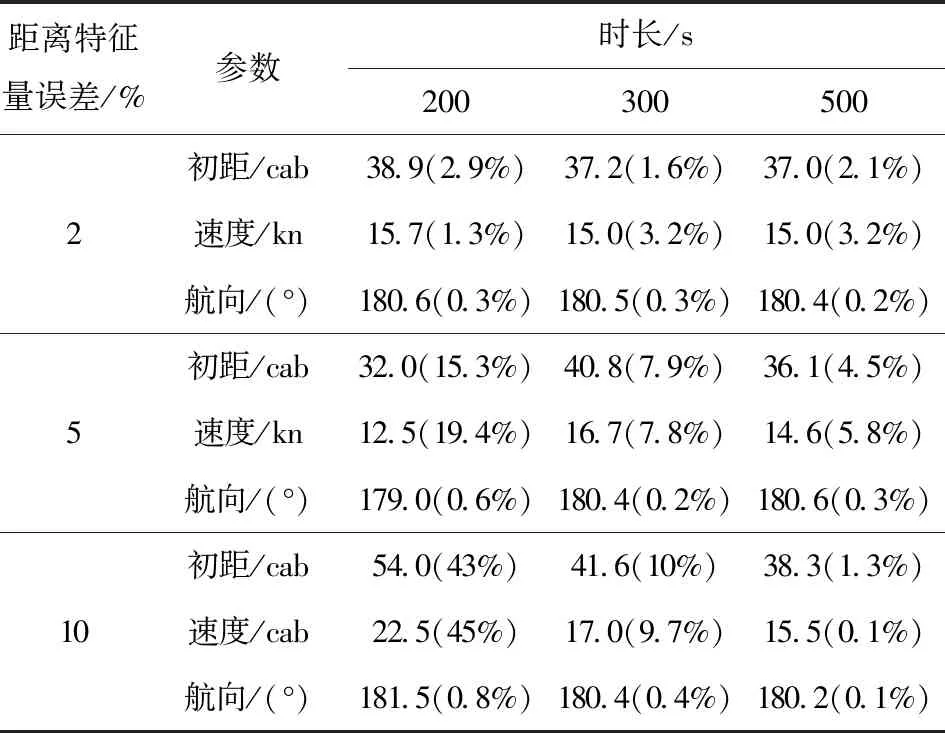
表1 距離特征量不同誤差時目標運動要素估計值與誤差

分析表1中的數據可知，當距離特征量誤差小于5%時，計算時長300 s即可獲得較準確的目標運動要素估計結果；當距離特征量誤差小于10%時，計算時長500 s可獲得準確的目標運動要素結果。隨著距離特征量誤差的增大，可視化圖中目標要素峰值主瓣越寬，峰值越不明顯，估計結果穩定性變弱。根據文獻[16-20]的分析，對于實際海上活動中穩定跟蹤的目標，其輻射噪聲時間- 頻率譜圖提取的距離特征量誤差一般小于5%.

圖16、圖17所示為當前仿真態勢條件下，目標方位誤差方差分別為0.3°和0.5°時目標運動分析(TMA)算法估計結果。由圖16和圖17可知，當目標要素解算收斂誤差小于10%時，解算時長分別為530 s和610 s左右，隨著方位誤差的增大，目標要素解算收斂用時增加。

分析以上仿真結果不難得出如下結論：基于距離特征量匹配尋優處理的目標運動分析方法，由于僅利用起始時刻和計算時刻兩個時間點的目標方位信息，可忽略方位誤差對算法的影響；對于距離特征量誤差在5%時，仍然能夠在300 s左右獲得較準確的目標要素估計，相比TMA算法在解算時長、精度上有較大改善。

3.2 試驗數據分析

選取某專項試驗獲取的數據對算法進行驗證。以航次A為例，試驗過程中目標船以航向350°、速度15 kn(約7.72 m/s)勻速直航，解算開始時刻目標距離聲吶平臺46 cab(約8.5 km)，目標方位182°. 圖18給出了A航次觀測平臺航向和航速信息。

試驗過程目標聲源輻射噪聲獲取的時間- 頻率譜如圖19所示。譜圖處理得到目標方位及距離特征量信息如圖20所示。基于距離特征量匹配處理的目標運動分析過程，在解算400 s時估計獲得的目標初距、速度和航向三要素可視化結果如圖21所示。給出的目標運動三要素結果分別為：目標初距為48.5 cab、速度為16.5 kn、航向為354°，誤差最大為目標速度估計結果約10%.

圖22～圖25所示為航次B中目標與聲吶平臺相互態勢信息、觀測平臺接收目標輻射噪聲時間- 頻率譜圖、估計的目標方位及距離特征量信息以及解算400 s時新算法獲取的可視化結果圖，其中目標初距、目標速度和目標航向真值分別為50.8 cab、15 kn和340°，算法估計結果分別為50 cab、14 kn和337°，目標各要素估計最大誤差為速度估計結果(誤差6.7%)。

分析2.2節算法的實現過程不難發現，該匹配方法由于僅利用到初始時刻和計算時刻兩個時間點的目標方位值，相比于傳統純方位目標運動分析，可有效規避目標方位觀測誤差的影響，更適應水中機動平臺的水聲目標運動分析問題。

以上仿真結果與試驗數據結果分析均表明，基于距離特征量匹配處理的目標運動分析方法，可通過處理目標輻射噪聲獲取的時間- 頻率譜圖獲得實時的目標距離特征量結果，結合目標初距、瞬距兩層循環尋優處理，利用本文構建的匹配代價因子可快速、準確估計目標運動三要素。

4 結論

本文以海洋聲場干涉結構特征為基礎，利用運動目標輻射噪聲時間- 頻率譜圖干涉條紋獲取目標距離特征量，將距離特征量信息引入目標運動分析過程，構建了基于實測距離特征量與目標運動分析估計距離特征量之間的匹配最優代價因子，基于匹配給出的可視化結果圖，實現目標運動三要素的估計。利用仿真和海試數據對算法進行了驗證，取得較好的實驗結果。得到主要結論如下：

1) 本文方法僅利用兩個時刻的目標方位信息，不需要實時量測目標方位，可有效規避存在于TMA算法中方位量測誤差對算法估計結果的影響。

2) 基于距離特征量匹配實現目標運動要素估計方法，能夠快速給出目標運動要素估計可視化結果圖，獲取的目標運動要素估計在時效性、準確性上相比TMA算法有較大改善。

3) 本文提出的基于聲干涉特征匹配的目標運動分析方法，適應于水下機動平臺的目標要素解算，易于工程實現，具有廣闊的應用前景。