剪刀式橋梁展橋機構鉸點位置多目標優化設計

韓軍， 朱鵬程， 張帥， 洪煌杰

(1.陸軍研究院 5所，江蘇 無錫 214035； 2.陸軍工程大學 野戰工程學院， 江蘇 南京 210007)

0 引言

剪刀式架設是軍用橋梁的一種典型架設方式，已在國內外軍用橋梁中得到廣泛應用。剪刀式架設的軍用橋梁有美軍JAB聯合沖擊橋、波蘭S-20沖擊橋[1]、英軍BR90橋梁族的近距離支援橋，以及我軍某型輪式沖擊橋、重型機械化橋[2]等。傳統的展橋機構采用雙油缸驅動、單油缸驅動鏈條展橋或鋼絲繩驅動翻轉架展橋，三者的共同特點是運輸狀態展橋機構突出橋節以外，增加了運輸長度，不利于裝備機動。英軍BR90近距離支援橋采用液壓機構實現橋梁的展開和撤收，實現了自動展橋功能[3]。

在展橋機構研究方面，為提高橋梁架設作業的平順性、架設速度和安全性，文獻[4]研究了軍用折疊橋梁機構架設軌跡優化及其自動控制問題。文獻[5]提出了一種新型救災用可展拱橋體系，包括可展橋體系、構件、連接、展開方式等；通過建立模型驗證了展橋的承載能力和結構性能，該展橋具有構件輕巧、運輸方便、施工快捷、承載力大等優點。文獻[6-7]介紹了一種新型剪刀式搶險機動橋，該橋采用剪刀式展開機構，在5～10 min內可架設20.8 m長的橋梁結構，橋體質量約為13 t，可以在受自然災害破壞的地方快速構筑橋梁通道，并通過試驗研究了該橋梁在自由和強迫載荷條件下的應變和動態特性。文獻[8]研究了剪刀式橋折疊和展開過程中的幾何特性、運動特性和結構響應問題，采用靈敏度分析方法評估分析了設計參數對剪刀橋的結構應力、變形和質量參數的影響。文獻[9]研究了一種基于鋁合金桁橋架的模塊化拱橋結構。文獻[10]研究了一種采用剪式鉸和套筒可展機構實現軸向展開的輕型展橋機構。

展橋機構是實現剪刀式橋梁架設的關鍵部件，由于展橋機構要求內置于橋節中，無論橋梁在折疊狀態還是在展開狀態下，均要求展橋機構不露出橋面，因此其外形結構要求緊湊，同時展橋機構采用油缸驅動，驅動油缸既要滿足折疊和展橋狀態要求即實現180°回轉，又要滿足一定的驅動力臂要求。另外，展橋機構是一個較復雜的單自由度多連桿機構，展橋過程是一種機構復合運動，機構的受力狀態復雜。在展橋機構中，其鉸點位置涉及展橋機構功能實現、驅動油缸選取及橋梁結構強度設計等因素，設計時僅憑經驗和機構仿真分析軟件，難以實現展橋機構鉸點位置的最優設計。

新型展橋機構在某型剪刀式橋梁上得到了應用，在方案樣機試驗過程中發現在橋梁架設的初始狀態，出現展橋機構驅動油缸的小腔由于壓力過大引起間斷液壓油溢流現象，為此需要開展展橋機構的優化設計工作。

本文介紹一種新型內置式軍用剪刀橋梁展橋機構[11]，其工作原理為，采用一個液壓油缸驅動轉架機構，實現橋節的折疊與展開，該機構具有結構簡單、緊湊，方便部隊機動等優點。利用Denavit-Hatenberg齊次變換矩陣[12]建立了展橋機構的運動學、靜力學和關鍵鉸點的多目標優化模型；結合工程實例對剪刀式橋梁展橋機構的關鍵鉸點進行了優化設計，并用ADAMS軟件對優化計算模型進行了驗證。

1 剪刀式橋梁工作原理與建模

1.1 工作原理

剪刀式橋梁由2個橋節組成，雙剪刀式橋梁由3個橋節組成，每兩個橋節通過展橋機構驅動，采用剪刀式作業原理，即架設時先展開我岸兩個橋節、再展開對岸橋節，從而形成兩次剪刀式展橋過程、完成架設作業。雙剪刀式橋梁展橋主要步驟(見圖1)如下：

步驟1運載車輛達到架橋點后，翻轉架油缸、頂起翻轉架，使橋跨置于垂直狀態；伸出支腿油缸，使礎板著地(見圖1(a))。

步驟2通過驅動舌形臂油缸和展橋油缸調整橋節角度，依次展開各橋節，直至橋跨完全展開(見圖1(b)、圖1(c))。

步驟3繼續伸舌形臂油缸，使舌形臂向右旋轉，直至橋跨端部與對岸著地(見圖1(d))。

1.2 展橋機構運動學建模

圖2所示為剪刀式橋梁結構示意圖，主要由翻轉架、第1橋節、第2橋節(含第3橋節)和展橋機構組成。圖中A、B、C、D、E、F、O、O1、O2、O3表示鉸點，翻轉架通過鉸點O1與第1橋節連接，由舌形臂油缸AB驅動第1橋節運動；第1、2橋節通過鉸點O2連接，其內部安裝有展橋機構，可以實現兩個橋節的運動。展橋機構由轉架O3EF、連桿EC和展橋油缸FD組成，其中轉架O3EF通過鉸點O3與第2橋節連接，通過連桿EC與第1橋節連接，展橋油缸FD的D點位于第2橋節上。工作時，展橋油缸驅動轉架旋轉，通過連桿帶動第1橋節旋轉(實際是第1橋節靜止、第2橋節運動)。展橋機構需要實現第1橋節與第2橋節的折疊和展開功能，且展橋機構需要在運輸和展開狀態下內置于橋體中，便于橋梁的運輸和工作。

下面建立展橋機構的運動學模型。以翻轉架與副車架的連接鉸點O為坐標原點，建立基{w}坐標系Oxy，在該坐標系中A點為翻轉架上舌形臂油缸支座；以第1橋節與翻轉架鉸接點O1為坐標原點，建立基{w1}坐標系O1x1y1，其中規定當第1橋節垂直地面時為初始狀態，此時y1軸方向豎直向上，在該坐標系中，B點為舌形臂油缸的另一端支座，C點為連桿EC鉸接點；以第1橋節與第2橋節鉸點O2為坐標原點，建立基{w2}坐標系O2x2y2，其中規定x2軸方向在初始狀態時與x1軸方向一致，在該坐標系中，D點為展橋油缸鉸點；以第2橋節與展橋機構鉸點O3為坐標原點，建立基{w3}坐標系O3x3y3，其中規定x3方向與轉架O3E方向一致，在該坐標系中，鉸點E為展橋機構與連桿的連接點，鉸接點F為展橋機構與展橋油缸的連接點。點G1、G2、G3和G4分別為第1橋節、第2橋節、展橋機構和展橋油缸的質心。各個坐標軸方向如圖2所示。

設θ1為{w1}坐標系相對于{w}坐標系的旋轉角度，wO1x、wO1y為O1點在{w}坐標系下的坐標；θ2為{w2}坐標系相對于{w1}坐標系的旋轉角度，w1O2x、w1O2y為O2點在{w1}坐標系下的坐標；θ3為{w3}坐標系相對于{w2}坐標系的旋轉角度，w2O3x、w2O3y為O3點在{w2}坐標系下的坐標。利用Denavit和Hartenberg齊次變換[12]，可建立兩節剪刀式橋梁的各個機構之間的姿態轉換矩陣為

(1)

(2)

(3)

(4)

(5)

(6)

(7)

(8)

(9)

采用類似方法，可得到其他鉸點和重心在坐標系{w}的坐標向量，從而可進一步確定剪刀式橋梁展橋過程中任意姿態下橋節與展橋機構各個鉸點的運動坐標、相互位置關系；相應地，可得到剪刀式橋梁的運動學模型。

1.3 展橋機構靜力學模型

由于架橋過程中的速度較低，在展橋過程某一狀態下，橋梁機構中的受力按靜力學模型處理。下面利用展橋機構的力和力矩平衡條件，對其進行求解。

由圖2，以橋整體結構為研究對象，由鉸點O1所受力矩平衡得∑MO1=0，有

f1·dO1AB-m1g(xm1-xO1)-m2g(xm2-xO1)-

m3g(xm3-xO1)-m4g(xm4-xO1)=0，

(10)

式中：f1為舌形臂油缸驅動力；dO1AB為力臂，表示鉸點O1到AB的距離；m1、m2、m3和m4分別為第1橋節、第2橋節(含第3橋節)、轉架和展橋油缸的質量；xm1、xm2、xm3、xm4分別為其質心在{w}坐標系下的x軸坐標；xO1為鉸點O1在{w}坐標系下的x軸坐標。

由水平方向的受力平衡得∑X=0，有

fO1x-f1cosα1=0，

(11)

式中：fO1x為支座鉸點O1所受到的水平分力；α1為舌形臂油缸的水平夾角。

由豎直方向的受力平衡得∑Y=0，有

fO1y-f1sinα1-(m1+m2+m3+m4)g=0，

(12)

式中：fO1y為支座鉸點O1所受到的垂直分力。

圖3中fO2x、fO2y分別表示鉸點O2所受到的水平分力和垂直分力。圖4中fO3x、fO3y分別表示鉸點O3所受到的水平分力和垂直分力。

以第1橋節為研究對象(見圖3)，由鉸點O2所受力矩平衡得∑MO2=0，有

-fO1y(xO2-xO1)+fO1x(yO2-yO1)-
f1dO2AB+m1g(xO2-xm1)-fEC·dO2EC=0，

(13)

式中：[xO2，yO2]、[xO1，yO1]分別為鉸點O2、O1在{w}坐標系下的坐標；dO2AB為力臂，表示鉸點O2到AB的距離；dO2EC為力臂，表示鉸點O2到EC的距離。

以轉架為研究對象(見圖4)，由鉸點O3所受力矩平衡得∑MO3=0，有

-f2·dO3FD+m3g(xO3-xm3)+
fEC·dO3EC=0，

(14)

式中：f2為展橋油缸驅動力；dO3FD為力臂，表示鉸點O3到FD的距離；xO3為鉸點O3在{w}坐標系下的x軸坐標；dO3EC為力臂，表示鉸點O3到EC的距離。

綜上所述，利用(1)式～(14)式就可以計算得到任意姿態下，舌形臂油缸、展橋油缸的驅動力臂dO1AB、dO3FD及其驅動力f1和f2.

2 展橋機構及其驅動油缸鉸點優化分析

在剪刀式橋梁中，展橋機構轉架O3EF的形狀、連桿CE中E鉸點的位置和展橋驅動油缸FD中D鉸點的位置，對展橋機構的功能實現及其展橋驅動油缸的受力狀態起著決定性影響。下面對其影響因素和制約條件進行分析。

首先，展橋機構需要滿足第1橋節和第2橋節展開成一字形和折疊的要求，實現架橋和折疊運輸的功能。其次，轉架O3EF在剪刀式橋梁展開和折疊狀態下滿足不露出橋面條件。再次，展橋驅動油缸應滿足最大伸長長度和最小安裝尺寸比例范圍要求。最后，各種展橋姿態下，展橋驅動油缸的最大驅動力(或壓力)最小化，以滿足展橋驅動機構的小型化和降低液壓系統工作壓力的要求。

為此，對連桿鉸點C、驅動油缸的鉸點D和展橋轉架O3EF各鉸點的位置進行優化設計。設各個鉸點的坐標為優化設計變量，分別為C(x1，y1)、D(x2，y2)、E(x3，y3)、F(x4，y4)，其中鉸點C為基{w1}下的坐標，鉸點D為基{w2}下的坐標，鉸點E和F為基{w3}下的坐標。

為了得到優化變量值，分兩步進行求解。

1) 已知第2橋節轉角θ2，求解轉架的旋轉角度θ3.

由于展橋機構為一個單自由度系統，根據展橋機構的運動學模型，以第2橋節轉角θ2為中間變量，利用轉橋機構中連桿CE在任意狀態下長度相等的約束條件，即

LCE(x1,y2,…,x4,y4)-
SCE(x1,y1,…,x4,y4,θ2,θ3)=0，

(15)

式中：LEC(x1,y1,…,x4,y4)為θ2=0和θ3=0條件下連桿CE的初始長度；SCE(x1,y1,…,x4,y4,θ2,θ3)為轉橋機構不同位置時連桿CE的長度。(15)式為

一個非線性方程，給定θ2值后，可利用優化算法求解該方程得到θ3值。

2) 利用多目標優化模型，對優化變量進行求解。

優化目標是：第1橋節在傾角θ1=-40°(經驗值，通常θ1∈[-43°,-35°])時，第2橋節轉角θ2∈[0°，180°]范圍內，展橋驅動油缸的驅動力f2(1)和閉鎖力f2(2)最大值最小化，并滿足展橋機構液壓驅動油缸的選型條件，即

minf(x1,y1,…,x4,y4)=
c(1)|f2(1)|+c(2)|f2(2)|，

(16)

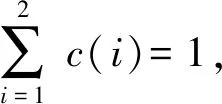
約束條件是：展橋驅動油缸的工作行程滿足最大行程和最小行程的比例范圍要求；三角轉架O3EF不翻轉及滿足三角形的邊長條件；展橋機構折疊和展開時，關鍵鉸點不露出橋面等；鉸點在空間布置上，滿足最低的安裝和布置條件等。

針對上述選取的優化變量，確定的約束條件以及優化目標，采用信賴域法[13]對(16)式優化模型進行求解。

3 方案樣機優化計算及驗證分析

3.1 方案樣機優化

某方案樣機已知優化變量值(經驗值)如表1所示。

表1 某方案樣機已知變量值

另外，已知第1橋節質量為500 kg，第2、3橋節質量為1 360 kg，轉架質量為35 kg，展橋油缸質量為45 kg，質心位置如圖1所示。

利用展橋機構的多目標優化計算模型，以θ1=-40°最常用的狀態為優化工況，依據展橋驅動油缸初步選型情況(最大閉鎖壓力為17 t，最大推力為26 t)，確定多目標的權重系數為0.395 3和0.604 9，可得到變量的優化值如表2所示。

表2 某方案樣機優化后變量值

將展橋機構優化后變量值代入力學計算模型，θ1分別取-35°、-40°和-43°，θ2的變化范圍為[0°，180°]，可得到優化前和優化后展橋機構驅動油缸推力f2的對比情況，分別如圖5～圖7所示。

由圖5可以看出，總體上，隨著第2橋節的展開，展橋油缸壓力變化由受拉狀態變化為0，然后逐漸變為受壓狀態，展橋油缸受力與實際的狀況吻合。優化前，θ2=0°時f2對應的最大拉力值-2.494 3×105N，θ2=75.6°時f2對應的最大推力值1.915 0×105N，液壓油缸的理想受力情況下，最大推力值(大腔作用)應大于最大拉力值(小腔作用)，而此時實際受力卻相反。同時也可從圖6、圖7看出，展橋機構驅動油缸的實際最大拉力值均大于最大推力值，展橋油缸受力狀態不合理，表明展橋機構鉸點設計不科學。

優化前模型所反映出的θ2=0°時展橋油缸所受拉力過大的問題，與方案樣機試驗過程中，在橋梁架設的初始狀態，展橋機構驅動油缸的小腔由于壓力過大引起間斷液壓油溢流現象相吻合，特別是在初始狀態θ2=0°時，θ1值越小(-43°)，液壓油缸所受拉力f2越大，過載情況越嚴重。

根據圖5～圖7的經驗值和優化后曲線數據，可得到展橋油缸最大拉力和最大推力值的情況比較如表3所示。

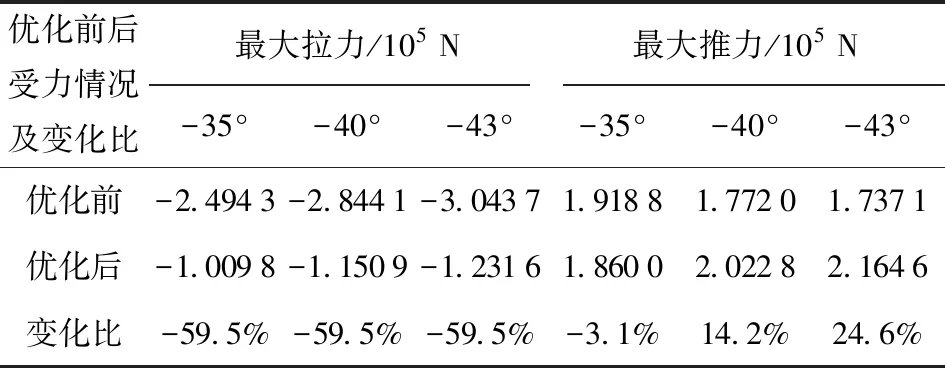
表3 優化前后展橋油缸受力情況比較

從表3中可以看出，優化后展橋油缸的最大受力狀態均有明顯改善，如在θ1=-35°時，最大拉力由-2.494 3×105N減小到-1.009 8×105N，降低59.5%，最大推力由1.918 8×105N減小到1.860 0×105N. 整體上，優化后展橋油缸的最大推力與最大拉力(閉鎖力)得到了明顯改善，如θ1=-35°時，最大推力約為最大拉力1.84倍的關系，與多目標優化的權重值基本一致，表明展橋油缸的受力合理，便于展橋油缸的選型，展橋機構鉸點優化值滿足設計要求。另外，不同于優化前，優化后θ1越大(-35°)，展橋驅動油缸受力狀況越好；θ1越小(-43°)，展橋驅動油缸受力狀況越差，與實際展橋油缸的受力狀態相一致。

鉸點優化后，展橋時四連桿機構CEO2O3中連桿O2O3轉角β、第2橋節轉角θ2和轉架O3EF轉角θ3的變化情況如圖8所示。從圖8中可以看出，第2橋節轉動180°時，β的變化范圍為[-90.229 5°,89.775 0°]，θ3的變化范圍為[-22.654 2°,80.961 9°]，轉架呈順時針轉動，變化曲線均略呈線性變化，機構轉動狀態連續平穩。

3.2 ADAMS驗證分析

利用機械系統動力學分析ADAMS軟件[14-15]建立剪刀橋的運動學模型，分別將優化前和優化后機械系統動力學分析變量作為輸入值，依據剪刀橋的結構參數，得到展橋機構的模型如9所示。

當θ1=-40°、θ2的變化范圍為[0°,180°]時，分別得到優化前和優化后，展橋油缸推力隨著第2橋節轉角θ2的變化曲線分別如圖10、圖11所示。

由圖10可以看到，當θ2=0°時展橋油缸受到的最大拉力為-2.837 6×105N，當θ2=86.1°時油缸的最大推力為1.776 4×105N，與本文的計算最大拉力-2.844 1×105N和最大推力1.772 0×105N值基本相同。由圖11可以看出，當θ2=0°時展橋油缸受到的最大拉力為-1.145 9×105N，當θ2=179.3°時油缸的最大推力為2.024 1×105N，與本文的計算最大拉力-1.150 9×105N和最大推力2.022 8×105N值基本相同。以上結果表明，本文的優化計算模型與ADAMS模型一致，優化模型正確。

4 結論

本文闡述了一種新型剪刀式橋梁展橋機構的工作原理，通過理論建模、工程樣機優化計算和驗證分析，得到以下主要結論：

1) 根據展橋油缸的閉鎖力和推力不同的特點，提出了滿足展橋油缸選型的展橋機構鉸點設計多目標優化計算方法，該方法有效可行。

2) 優化后，方案樣機展橋油缸的最大拉力降低幅度達59.5%，解決了方案樣機架橋初始狀態展橋油缸由于壓力過大出現間斷溢流問題。同時，展橋油缸的最大推力和最大拉力分布趨于合理，展橋機構的功能滿足設計要求。

3) 優化計算方法具有穩定、收斂快等特點，ADAMS仿真結果表明計算模型的正確性，研究結果為工程樣機的改進提供了重要依據。