發(fā)散 收斂 歸元
——從一道中考題談化學(xué)分析計(jì)算題的解題策略
金 典 金 隆
(1.浙江省天臺(tái)中學(xué) 317200;2.浙江省天臺(tái)縣教育局教研室 317200)
《中學(xué)化學(xué)課程標(biāo)準(zhǔn)(2017版)》提出的化學(xué)學(xué)科核心素養(yǎng)中包含:“能多角度、動(dòng)態(tài)地分析化學(xué)反應(yīng),運(yùn)用化學(xué)反應(yīng)原理解決實(shí)際問(wèn)題.具有證據(jù)意識(shí),能基于證據(jù)對(duì)物質(zhì)組成、結(jié)構(gòu)及變化提出可能的假設(shè),通過(guò)分析推理加以證實(shí)或證偽;建立觀點(diǎn)、結(jié)論和證據(jù)之間的邏輯關(guān)系” .《浙江省初中畢業(yè)升學(xué)考試說(shuō)明》中的題型分布明確解答題占比約28%.
化學(xué)式、化學(xué)方程式和質(zhì)量守恒定律是化學(xué)學(xué)科的獨(dú)有語(yǔ)言、核心知識(shí),是化學(xué)學(xué)科素養(yǎng)的重要組成.2017年,浙江的10個(gè)地區(qū)初中科學(xué)中考試題中均出現(xiàn)根據(jù)化學(xué)方程式及化學(xué)式進(jìn)行分析和計(jì)算,有6個(gè)地區(qū)考查應(yīng)用質(zhì)量守恒定律解釋現(xiàn)象,見表1;近5年,臺(tái)州地區(qū)的科學(xué)中考卷中化學(xué)獨(dú)立計(jì)算題有1~3題,分值在5~10分之間,占比4%左右,見表2;2018年,浙江10個(gè)地區(qū)在考查獨(dú)立化學(xué)計(jì)算題的分值上雖然不均衡,但總體比前幾年的占比有所上升,說(shuō)明評(píng)價(jià)加大了對(duì)學(xué)生利用化學(xué)知識(shí)運(yùn)算能力的考查,見表3.利用化學(xué)計(jì)算題,是測(cè)定學(xué)生掌握化學(xué)式、化學(xué)方程式和質(zhì)量守恒定律的有效工具,所以也就出現(xiàn)了該種題型“年年考,重復(fù)考”的現(xiàn)象.

表1

表2
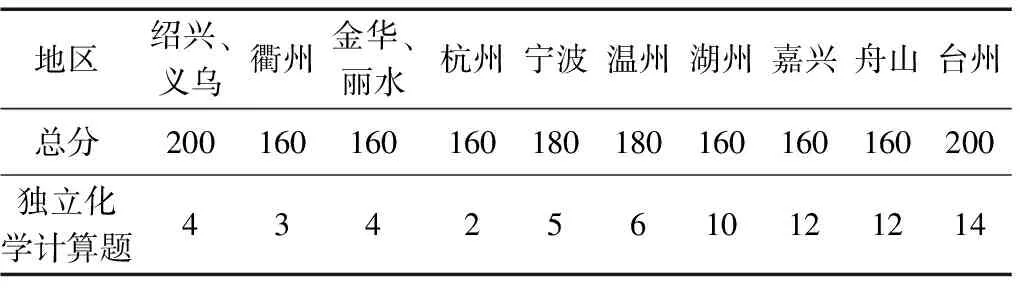
表3
下面主要以臺(tái)州地區(qū)2018年初中科學(xué)中考第35題(2)獨(dú)立化學(xué)計(jì)算題為例,探討該題型解題的方法、策略和思想.
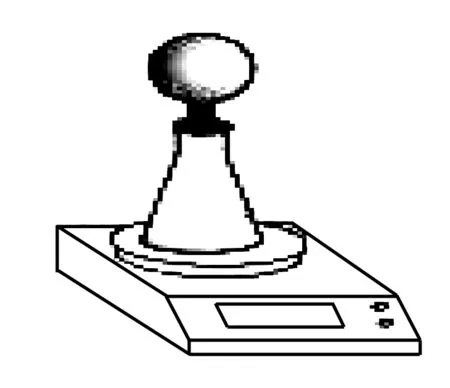
例(臺(tái)州·2018·35)某同學(xué)用如圖裝置驗(yàn)證質(zhì)量守恒定律.稱取一定質(zhì)量的碳酸鈉裝入氣球,將氣球套在錐形瓶上.將藥品全部倒入裝有足量稀鹽酸的錐形瓶中,氣球迅速脹大.稱量反應(yīng)前后裝置的總質(zhì)量,實(shí)驗(yàn)數(shù)據(jù)如下表所示.
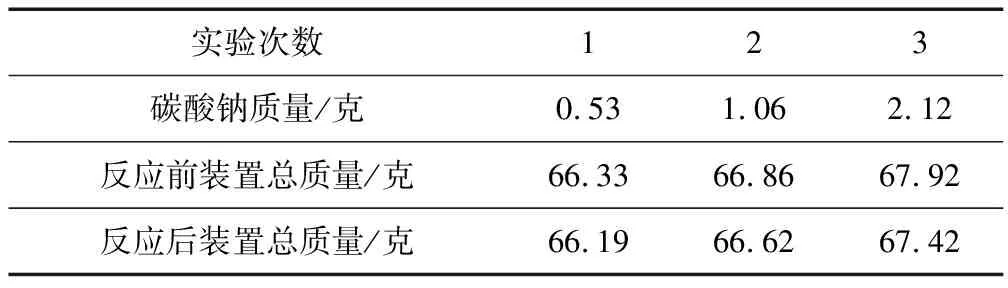
實(shí)驗(yàn)次數(shù)123碳酸鈉質(zhì)量/克0.531.062.12反應(yīng)前裝置總質(zhì)量/克66.3366.8667.92反應(yīng)后裝置總質(zhì)量/克66.1966.6267.42
(1)計(jì)算第1次反應(yīng)產(chǎn)生的二氧化碳質(zhì)量.
(2)分析數(shù)據(jù)發(fā)現(xiàn)每次反應(yīng)前后裝置的總質(zhì)量均不相等,請(qǐng)以第1次反應(yīng)為例,通過(guò)計(jì)算說(shuō)明該反應(yīng)是否遵循質(zhì)量守恒定律.(空氣密度取1.3 g/L,二氧化碳密度取2.0 g/L,結(jié)果精確到0.01)
第一小題的常規(guī)解法見下:
解(1)設(shè)第1次反應(yīng)產(chǎn)生的二氧化碳質(zhì)量為x.

106 44
0.53 gx
106∶44=0.53 g∶xx=0.22 g
答:第1次反應(yīng)產(chǎn)生的二氧化碳質(zhì)量是0.22g.
一、以多元的發(fā)散性思維尋找解題方法
1.利用化學(xué)方程式計(jì)算
解法1(1) Δm=66.33 g-66.19 g=0.14 g
m(CO2)=ρ(CO2)V(CO2)=2.0 g/L×0.11 L
=0.22 g
(2)設(shè)產(chǎn)生0.22 g二氧化碳需要x的碳酸鈉

106 44
x0.22g
106∶44=x∶0.22 g
x=0.53 g=反應(yīng)前碳酸鈉的質(zhì)量
所以符合質(zhì)量守恒定律.
該解法利用各物質(zhì)質(zhì)量差和密度關(guān)系先求出(1)產(chǎn)生的二氧化碳質(zhì)量,再利用化學(xué)方程式從已知產(chǎn)物質(zhì)量倒求反應(yīng)物質(zhì)量,證實(shí)質(zhì)量守恒.解法運(yùn)用了質(zhì)量守恒定律、化學(xué)式和化學(xué)方程式等化學(xué)核心知識(shí),蘊(yùn)含了逆向思維,是解決化學(xué)計(jì)算題較為常見的解題思路.計(jì)算中各物質(zhì)的質(zhì)量比也可以轉(zhuǎn)換成摩爾比進(jìn)行.
2.利用化學(xué)式計(jì)算

在題設(shè)充分反應(yīng)的前提下,該解法巧妙地利用化學(xué)式中的比例關(guān)系,根據(jù)質(zhì)量守恒思想進(jìn)行計(jì)算,過(guò)程簡(jiǎn)潔明了,結(jié)果準(zhǔn)確可靠.
3.利用密度計(jì)算
解法3(2)Δm=66.33 g-66.19 g=0.14 g
m排空氣=ρ空氣V空氣=ρ空氣V(CO2)
Δm=m排空氣
所以遵守質(zhì)量守恒定律.
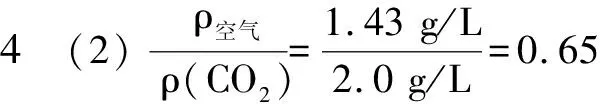
m排空氣=0.65m(CO2)=0.65×0.22 g=0.14 g
m排空氣+m反應(yīng)后=0.14g+66.19g=66.33g=m反應(yīng)前
所以遵守質(zhì)量守恒定律.
解法5(2)Δm=66.33 g-66.19 g=0.14 g
V排=V(CO2)
所以遵守質(zhì)量守恒定律.
解法6(2)Δm=66.33 g-66.19 g=0.14 g
ρ(CO2)的計(jì)算值與題設(shè)所給條件一致,所以遵守質(zhì)量守恒定律.
解法3~解法6在第(1)小題已經(jīng)算出二氧化碳質(zhì)量為0.22 g的基礎(chǔ)上,圍繞密度公式求預(yù)設(shè)未知量,與題設(shè)所給已知量進(jìn)行比較,得出結(jié)論.四種解法雖然路徑各異,但解題均依據(jù)核心知識(shí)密度公式進(jìn)行變式發(fā)散.
4.利用浮力、重力計(jì)算
解法7Δm=66.33 g-66.19 g=0.14 g
F浮=Δmg=0.14 g×10 N/kg=1.4×10-3N
m(CO2)=ρ(CO2)V(CO2)=2.0 g/L×0.11 L=0.22 g
所以遵守質(zhì)量守恒定律.
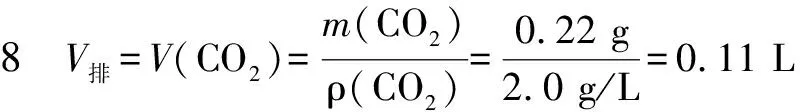
F浮=ρ空氣gV排=1.43 g/L×10 N/kg×0.11 L=1.4×10-3N
G反應(yīng)前=m反應(yīng)前g=66.33 g×10 N/kg=66.33×10-3N
G反應(yīng)后=m反應(yīng)后g=66.19 g×10 N/kg=66.19×10-3N
G反應(yīng)后+F浮=G反應(yīng)前
所以遵守質(zhì)量守恒定律.
臺(tái)秤讀數(shù)的變化,直接原因是作用在秤盤上的壓力減小,根本原因是發(fā)生化學(xué)變化釋放二氧化碳?xì)怏w,氣球體積膨大,所受浮力增大導(dǎo)致.這兩種特別是第8種解法,較好地還原了問(wèn)題情境的發(fā)生原因,呈現(xiàn)了符合學(xué)生認(rèn)知規(guī)律的解題思維路徑.
二、以聚合性思維收斂解題策略
與發(fā)散性思維相對(duì)應(yīng),聚合性思維是指從不同來(lái)源、不同材料、不同層次探求出一個(gè)正確答案的思維方法,是一種有方向、有范圍、有條理的收斂性思維方式.細(xì)究上述8種解題方法,甄別歸類后不外乎比例法、差量法和等值法三種.
1.比例法
利用化學(xué)方程式計(jì)算其本質(zhì)就是利用比例解決問(wèn)題;利用化學(xué)式計(jì)算中也存在大量的比例法.解法1、2、4都較好地體現(xiàn)了這種解題策略.
2.差量法
在化學(xué)變化引起量變?nèi)缟蓺怏w、沉淀等的大量情景問(wèn)題中,分析問(wèn)題發(fā)生的起始狀態(tài)和終止?fàn)顟B(tài),審視題設(shè)給予的發(fā)生條件,結(jié)合科學(xué)原理歸因,便可找到量變的原因,從而理順解題思路.解法3、5、6、7都有這種解題策略的應(yīng)用.
3. 等值法
質(zhì)量守恒是化學(xué)學(xué)科的核心知識(shí)、是科學(xué)普遍和統(tǒng)一的原理和規(guī)律,解釋化學(xué)現(xiàn)象和事實(shí)、解決化學(xué)問(wèn)題、預(yù)測(cè)化學(xué)變化始終繞不開這一規(guī)律.抓住質(zhì)量守恒,我們就可以排除紛雜的變化現(xiàn)象,直達(dá)化學(xué)變化中質(zhì)量變化的本質(zhì),尋獲解決問(wèn)題的鑰匙.8種解法都應(yīng)用到了這種解題策略.
美國(guó)數(shù)學(xué)家波利亞在《怎樣解題》的擬訂方案中提示解題者“你以前見過(guò)它嗎?或者你見過(guò)同樣的題目以一種稍有不同的形式出現(xiàn)?”.本文提供了8種該題的解法,實(shí)際有可能更多,但從解題策略歸類大體均屬以上三種.“授之以魚不如授之以漁”,課程標(biāo)準(zhǔn)的三維目標(biāo)中也突出“過(guò)程與方法”,不管眾多發(fā)散性的解題過(guò)程如何表述,只要我們學(xué)會(huì)解題方法的歸類,使解題策略簡(jiǎn)化、純化和模式化,解題必可事半功倍.
三、以批判性思維歸元解題思想
道家哲學(xué)的返本歸元,就是“返本還原、與道體合一、回歸自然、回歸原始”,是一種 “道”.文學(xué)家說(shuō)散文“形散而神不散”;武學(xué)家說(shuō)武術(shù)最高境界是“殊途同歸”;教學(xué)家說(shuō)“教有教法、教無(wú)定法、貴在得法”.解題也有道,可使我們?cè)诿C5念}海中回頭是岸.如果你不能解所提的題目,波利亞說(shuō):“回到定義上去”、“你把題目中所有關(guān)鍵的概念都考慮到了嗎”;廣西師大袁守華教授在他的《物理解題思維的理論和方法》中指出“物理解題思維的特點(diǎn)是:基于物理模型的定性現(xiàn)象分析與物理公式的定量計(jì)算相結(jié)合”,這種特點(diǎn)在跨界、整合和綜合的STEM課程等眾多領(lǐng)域也廣泛存在.
在實(shí)現(xiàn)知識(shí)的概念化(是什么)、條件化(怎么用)、結(jié)構(gòu)化(網(wǎng)絡(luò)化)和自動(dòng)化(近乎條件反射)之后,我們才能形成解決問(wèn)題的一般思維策略.通過(guò)審題,我們對(duì)題設(shè)進(jìn)行分割、重組和匹配,尋找相應(yīng)的化學(xué)模型、定義、概念、原理和公式等解題原理,轉(zhuǎn)變成解題者的自我語(yǔ)言重新理解、表述.化學(xué)計(jì)算題的解題原理集中在化學(xué)式、化學(xué)方程式和質(zhì)量守恒定律,部分整合跨學(xué)科如物理的力學(xué)、密度等知識(shí).只要把題目中所有關(guān)鍵的概念都考慮到,不管題設(shè)情景如何新穎、干擾信息如何紛紜,我們“弱水三千,只取一瓢飲”,問(wèn)題總能迎刃而解.
解題的“元”就是學(xué)科核心素養(yǎng)中的核心知識(shí)、信息意識(shí)、思維品質(zhì)和實(shí)踐創(chuàng)新,具體物化的有《學(xué)科課程標(biāo)準(zhǔn)》和《考試說(shuō)明》.在學(xué)教方式變革的深課改熱潮中,只有轉(zhuǎn)變分析、評(píng)價(jià)和創(chuàng)新的思維方式,才能促進(jìn)“學(xué)評(píng)統(tǒng)一”,度茫茫題海之苦.

